Ecological Footprint and Population Growth Models

This study material discusses the concept of ecological footprint and population growth models. It explores the impact of human population on the Earth's biocapacity and the sustainability of current arrangements. It also explains unlimited population growth models and the Verhulst model. The material provides calculations for population growth rates and carrying capacity.

Part A: Ecological Footprint
1) The human population has been clearly living beyond the Earth’s natural biocapacity which
is apparent from Figure 1 which illustrates that the ecological footprint of the human being
exceeds 1. This has been the situation since 1971 when the ecological footprint crossed 1 for
the first time and has been on the rise since then. Clearly, this situation is not sustainable as it
would cause irreparable damage to the ecological balance of our planet.
2) The Australian population is living below Australia’s natural biocapacity. Based on figure 3,
this has always been the case. From 1961 to 2012, the above observation is true. The
sustainability of the current arrangement is in jeopardy as during the last five decades, the
positive gap between biocapacity and ecological footprint has been decreasing and hence
going forward it may happen that EF may exceed biocapacity.
3) The US population has been clearly living beyond the US natural biocapacity which is
apparent from Figure 4 which illustrates that the ecological footprint of US population
exceeds the biocapacity of US. This has been the situation for the complete period captured
in the graph (1961 to 2012). Clearly, this situation is not sustainable as it would cause
irreparable damage to the ecological balance in US (and elsewhere) and increase the
incidence of various adverse natural phenomena.
4) The slope of ecological footprint of Australia can be estimated using the following
information.
EF for 2012 = 9.3
EF for 1961 = 8
Total years = 2012-1961 = 51
Total change in EF = 9.3 – 8 = 1.3
Hence, slope = (1.3/51) = 0.0255 global hectare per person

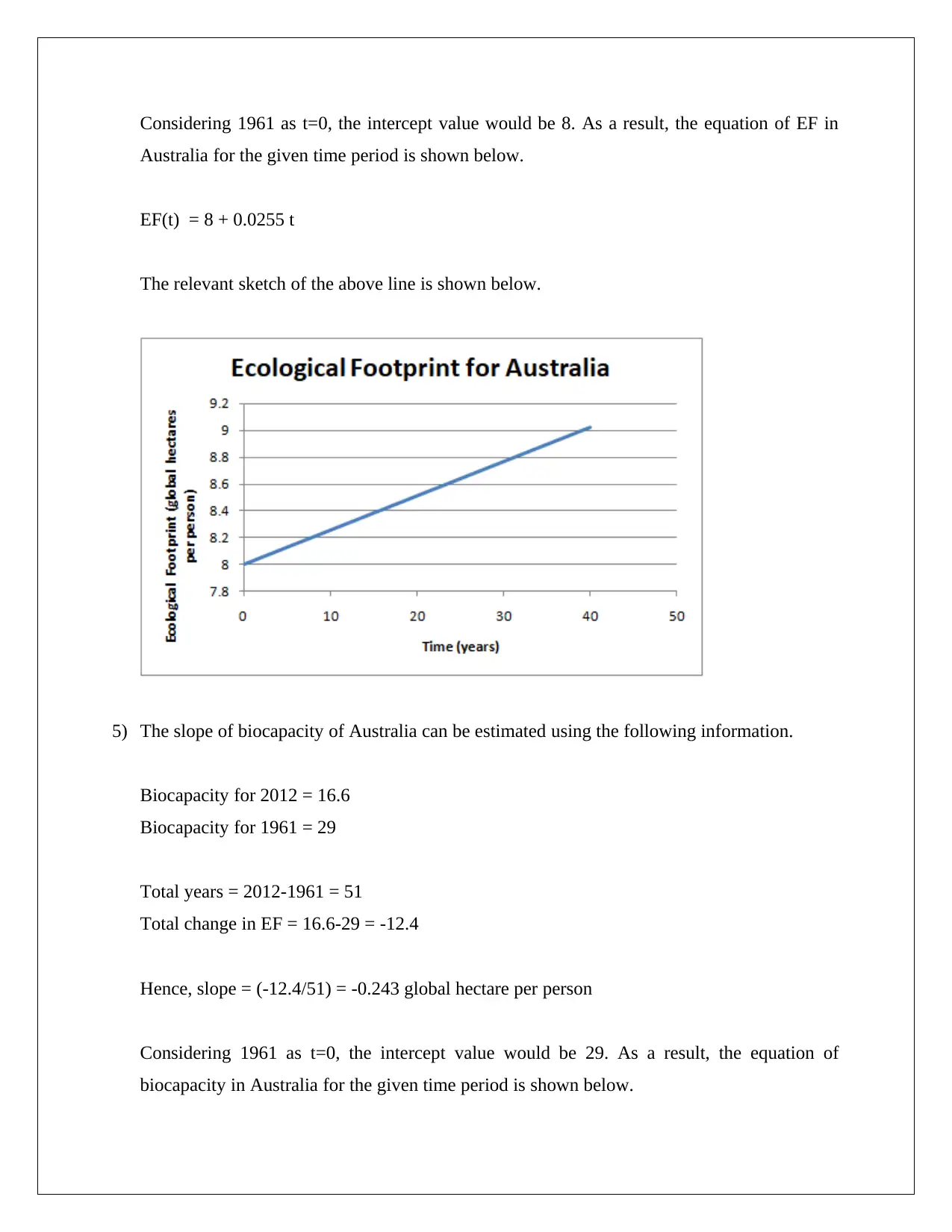
Considering 1961 as t=0, the intercept value would be 8. As a result, the equation of EF in
Australia for the given time period is shown below.
EF(t) = 8 + 0.0255 t
The relevant sketch of the above line is shown below.
5) The slope of biocapacity of Australia can be estimated using the following information.
Biocapacity for 2012 = 16.6
Biocapacity for 1961 = 29
Total years = 2012-1961 = 51
Total change in EF = 16.6-29 = -12.4
Hence, slope = (-12.4/51) = -0.243 global hectare per person
Considering 1961 as t=0, the intercept value would be 29. As a result, the equation of
biocapacity in Australia for the given time period is shown below.

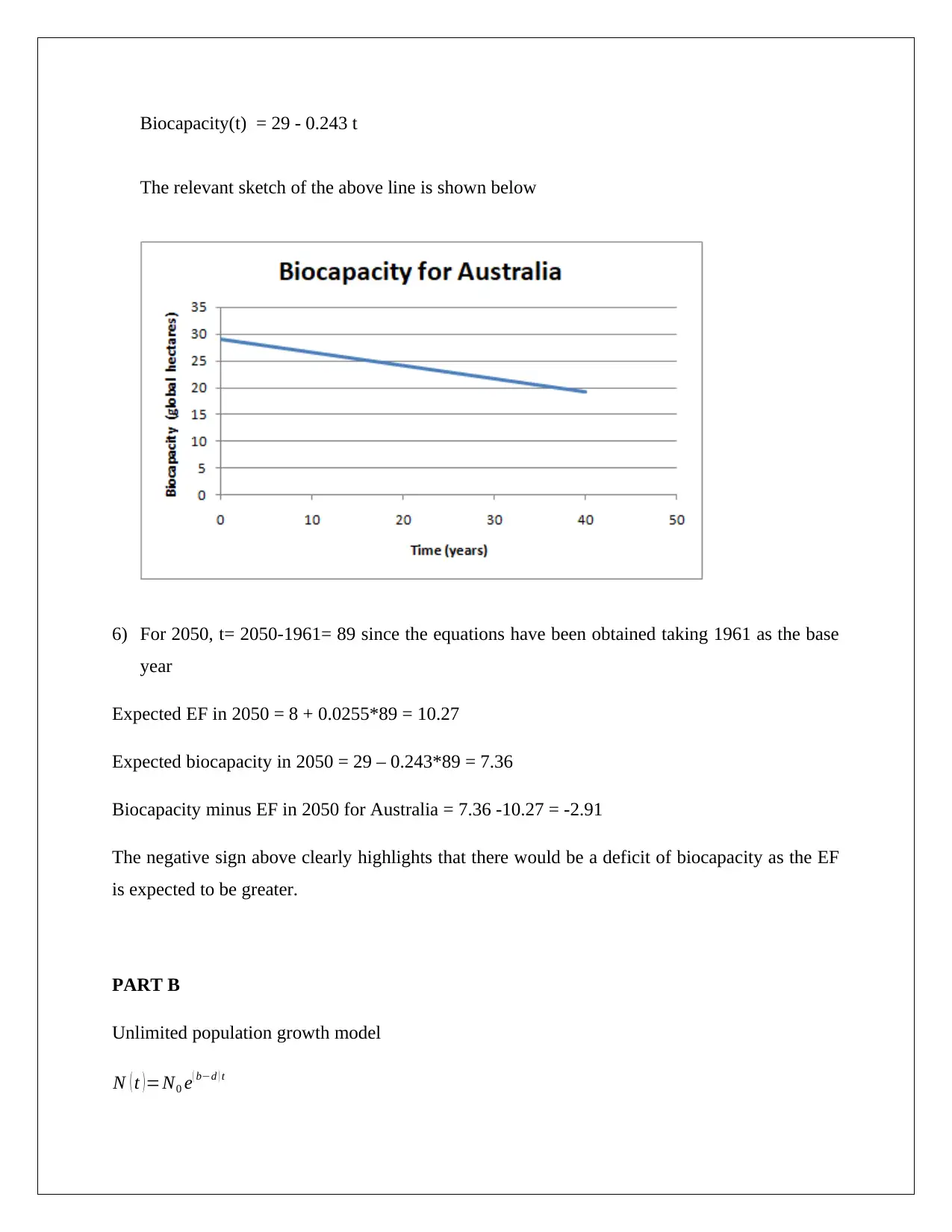
Biocapacity(t) = 29 - 0.243 t
The relevant sketch of the above line is shown below
6) For 2050, t= 2050-1961= 89 since the equations have been obtained taking 1961 as the base
year
Expected EF in 2050 = 8 + 0.0255*89 = 10.27
Expected biocapacity in 2050 = 29 – 0.243*89 = 7.36
Biocapacity minus EF in 2050 for Australia = 7.36 -10.27 = -2.91
The negative sign above clearly highlights that there would be a deficit of biocapacity as the EF
is expected to be greater.
PART B
Unlimited population growth model
N ( t )=N0 e
( b−d ) t

1) Population after 1 year (t =1) =?
Initial population N0=1000
Annual birth rate b=0.02
Annual death rate d=0.01
N ( t )=N0 e( b−d ) t= ( 1000 ) e (0.02−0.01 )1=1000 e0.01=1010.05
Hence, the population after 1 year is 1010. This implies that the net growth in population in a
year is 2% -1% = 1% approximately.
2) Expression for growth rate or population change can be indicated by differentiating the
function provided.
d N ( t )
dt = d
dt ( N0 e( b−d ) t )
d N ( t )
dt =N0 (b−d )e ( b −d ) t
3) If d is less than b, then the above expression would be positive. This is on expected lines as
the lower death rate in comparison to birth rate would imply that the population would grow.
As a result, the growth rate would be positive which has been indicated by the dN(t)/dt
expression computed in part (2).
PART C
1) Unlimited population growth with harvesting model
N ( t ) =a e ( b−d ) t + H−H e ( b−d ) t
(b−d)

Where,
b=birth rate
d=death rate
H=number of individual taken¿ population
Now,
d N ( t )
dt = d
dt ( a e ( b −d ) t + H−H e ( b −d ) t
( b−d ) )
d N ( t )
dt = d
dt ( a e (b−d ) t ) + d
dt ( H− H e (b −d )t
( b−d ) )
d N ( t )
dt =a ( b−d ) e( b−d ) t + 1
b−d∗¿
d N ( t )
dt =a ( b−d ) e( b−d ) t− H ( b−d ) e ( b −d ) t
(b−d )
d N ( t )
dt =a ( b−d ) e ( b−d ) t−H e ( b−d ) t
d N ( t )
dt = ( b−d ) N ( t )−H
2) Initial population N0=1000
Annual birth rate b=0.05
Annual death rate d=0.01
H = sustainable harvest =?
d N ( t )
dt = ( b−d ) N ( t )−H

d N ( t )
dt =0
( b−d ) N ( t )−H =0
( 0.05−0.01 )∗1000−H=0
H=40
The sustainable harvest value is 40 for which there would no change in the overall population.
3) In the given case there has been a decline in the population owing to which 4% of the
individuals perish. As a result, the remaining population is lower based on which the
harvesting quantity H for sustainable harvest would reduce.
Assuming the values given in part (2) and population of 1000*(1-0.04) = 960, the computation of
H is shown as follows.
( 0.05−0.01 )∗960−H=0
H=38.4
It is evident that H has reduced but the harvesting continues at the previous rate of 40 which is
not sustainable and would cause the population to shrink going forward.
4) If one fish is thrown back, then the population of the fish would increase which would lead to
a higher value of sustainable harvest than the present value H. Since the harvest continues at
the original value H (40), thus, in the long run this would cause an increase in the population
since the harvest rate observed is lower than the harvest rate that should be practiced so as to
keep the population of fish constant. Besides, as the population of fish keep on increasing,
the value of sustain harvest H would keep on increasing from the current value of 40 giving
rise to an exponential rise in the quantity of fish which would potentially reach infinity in the
long run.

5) This is called a knife edge equilibrium since the replacement rate should be precisely equal to
the harvest rate in order to maintain a constant population of the underlying species. Any
deviation from the above even by a small amount can potentially have significant amount on
the population of species which would witness exponential change in either direction based
on whether replacement rate is lower or higher than the harvest rate.
PART D
1) Verhulst model
N ( t )= N0 ert
1+ N0 (ert −1)
K
N0=0(Initial population is zero)
Growth rate would also be zero when the initial population is zero since N(t) would always
remain 0.
2) When population is initially at carrying capacity
N0= K
Now,
N ( t ) = K ert
1+ K (ert −1)
K
N ( t )= K ert
1+ ert −1
N ( t )= K ert
ert
N ( t )=K

Hence, it can be said that when the population is initially at carrying capacity then the population
at any time t would also be at carrying capacity. Clearly, there is no influence of the changes in
growth rate in this case as the population at time t is independent of the underlying growth rate
for this particular case.
3) Population growth at time t is computed below.
N ( t )= N0 ert
1+ N0 (ert −1)
K
dN ( t )
dt = d
dt { N0 ert
1+ N0 ( ert−1 )
K }
dN ( t )
dt =N 0
d
dt { ert
1+ N 0 ( ert −1 )
K }
Applying the quotient rule
dN ( t )
dt =N 0
{ ( 1+ N 0 ( ert −1 )
K ) d
dt ert −ert d
dt ( 1+ N0 ( ert−1 )
K )
( 1+ N0 ( ert−1 )
K ) 2
}
dN ( t )
dt =N 0
{ ( 1+ N 0 ( ert −1 )
K ) r ert −ert
( N0 r ert
K )
( 1+ N0 ( ert−1 )
K )
2
}

dN ( t )
dt = N 0 r ert
( 1+ N0 ( ert−1 )
K )
2 {( 1+ N 0 ( ert −1 )
K ) − N0 ert
K }
dN ( t )
dt = N 0 r ert
(1+ N0 ( ert−1 )
K )2 {1+ N0 ert
K − N0
K − N0 ert
K }
dN ( t )
dt =r N0 ert
( 1+ N0 ( ert−1 )
K )
2 {1− N0
K }
dN ( t )
dt =r N ( t ) ( 1− N (t)
K )
Hence, Proved!
4) From the above expression for population growth, one of the term is ( 1− N (t )
K ). If the
population at a given time is greater than K, then the above term would become negative
which would imply the growth rate is negative, hence implying that the population is
decreasing. Thereby, the population growth rate would be faster when N is lesser than K
since this would lead to a positive growth rate.
5) Carrying capacity = K = 100,000
Population of the year = N0 = 90,000
Reproduction ratio = r = 2%
Number of fish that can be harvested per year
dN ( t )
dt =0.02∗90,000 (1− 90,000
100,000 )=18 0