Material to Build a Pedestrian Bridge - VEN1104
VerifiedAI Summary
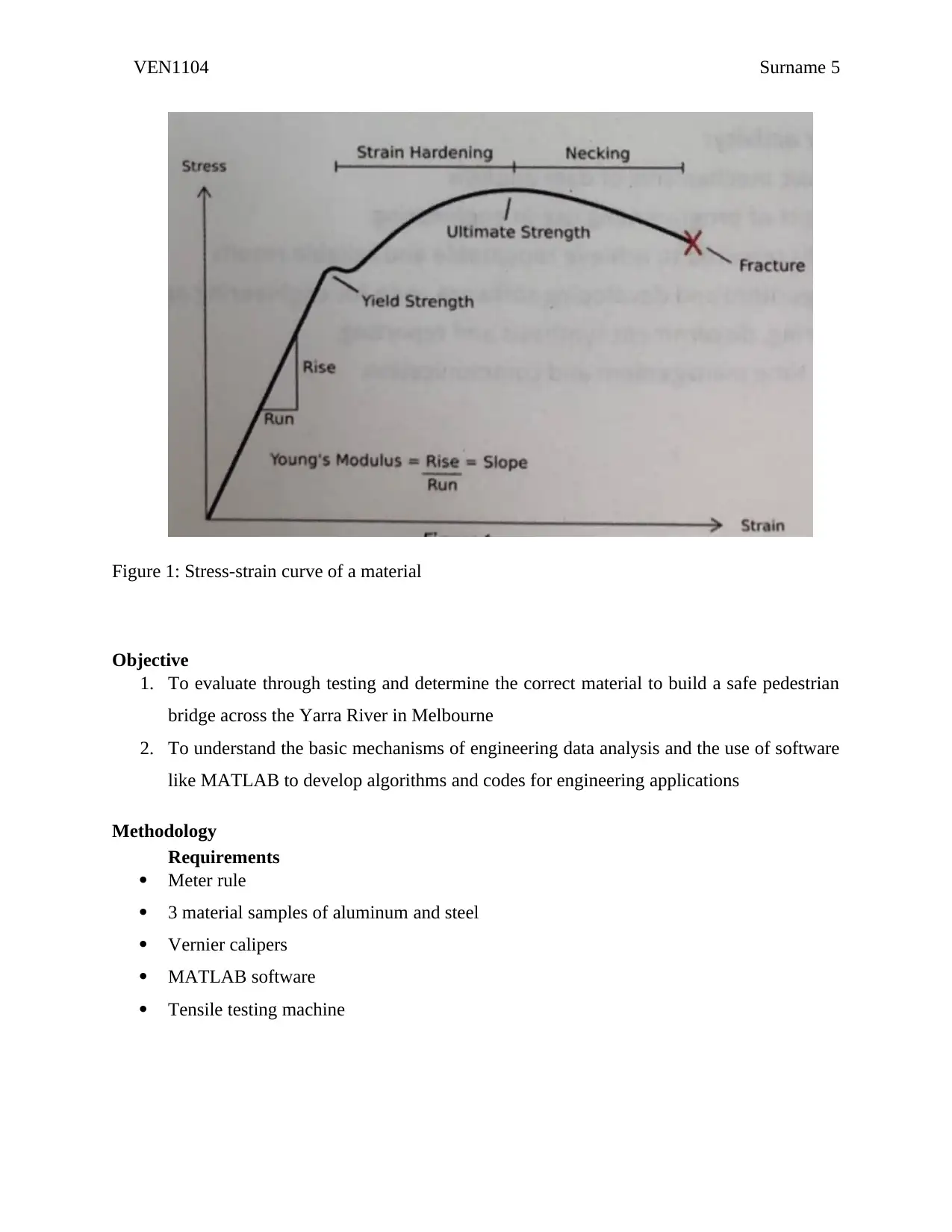
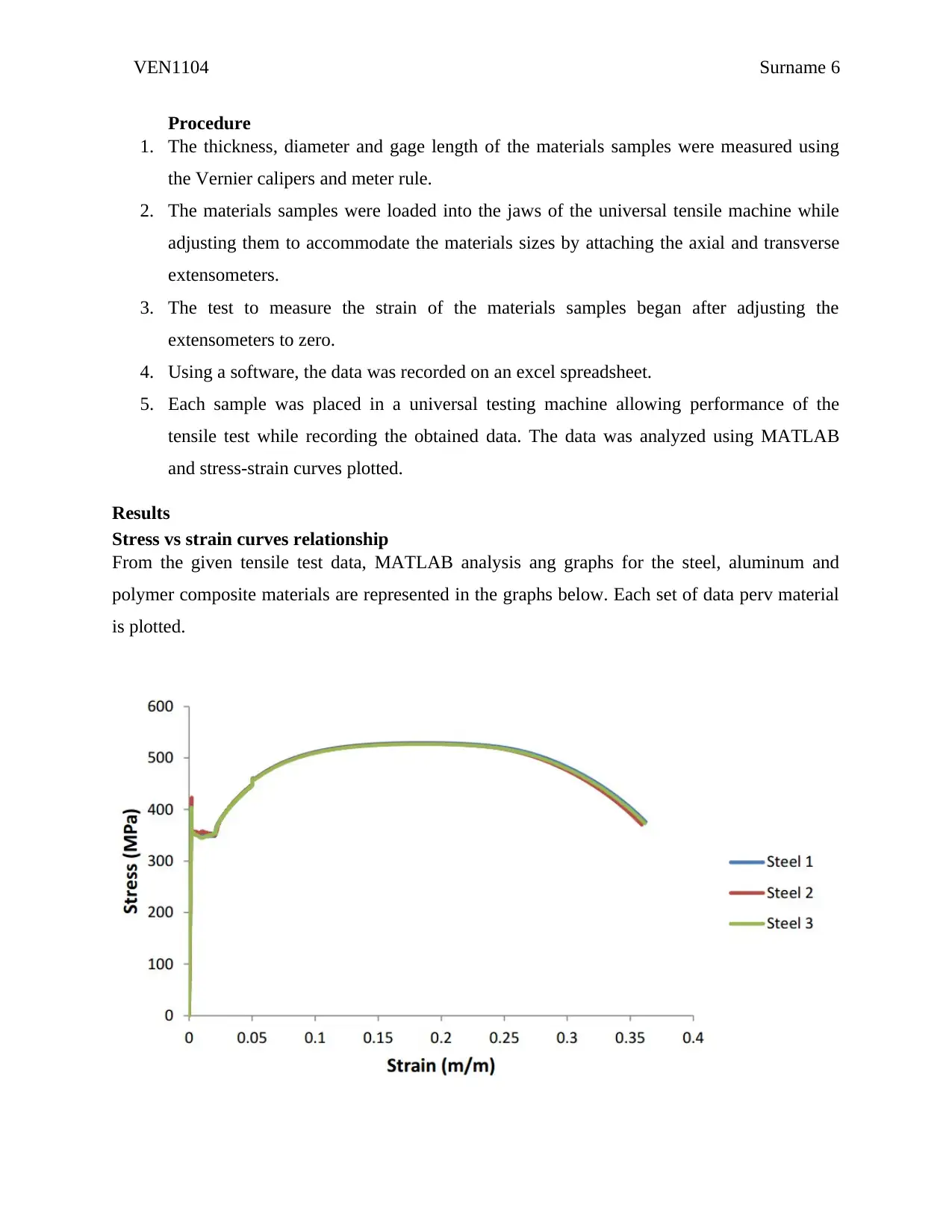
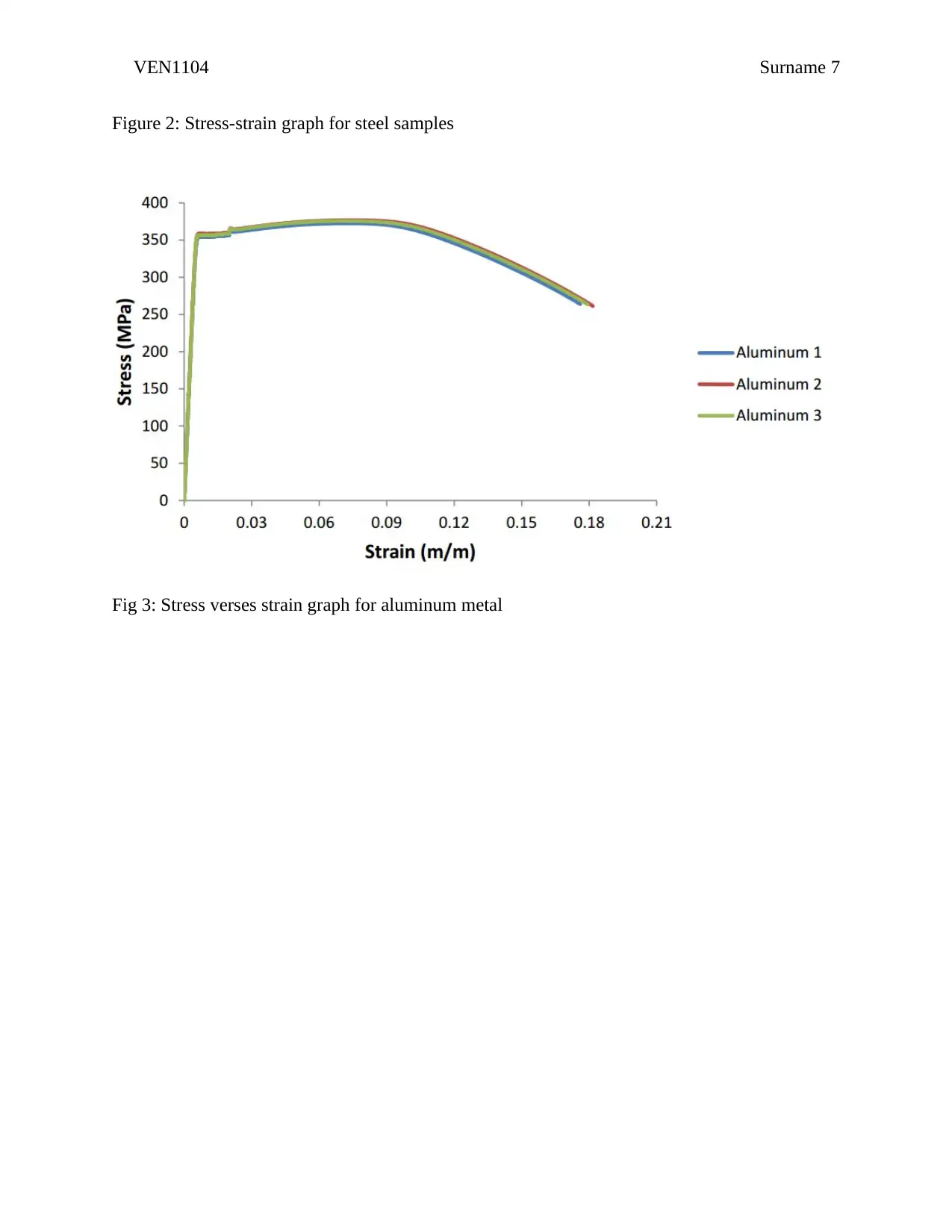
This experiment was conducted to evaluate and determine the correct material to build a pedestrian bridge across the Yarra River. The strength of the material used exceeded 9kN/m for safety factors. Tensile testing of various materials was used to select the suitable material for the pedestrian bridge construction. The stress-strain relationship of the materials was use to predict their behaviors when subjected to various loading conditions. MATLAB programming was used to evaluate the obtained tensile testing data. The experimental results recommend the use of steel in the construction of the bridge due to its strength properties that enables it to withstand high axial loading as compared to other materials. The strength exceeds the recommended one of 9Kn/m.
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)