Perimeter, Area, Volume, Pythagoras Theorem and Trigonometric Ratios

This assessment task is based on the knowledge of perimeter, area, volume, surface area, Pythagoras Theorem and Trigonometric ratios. It consists of 7 problem solving questions. The questions are related to finding the lengths of missing sides, calculating perimeter and area of shapes, calculating volume of soil, calculating surface area of excavated vegetable patch and calculating the volume of composite soil needed. The output is in json format.

Assessment Task 4
Assessment Task Title:
Assessment Task 4: Perimeter, area, volume, Pythagoras Theorem and Trigonometric
ratios
Student Name Thomas Scifo
Student ID S4645762
This knowledge test assessment is based on the information you have studied in your
classroom activities, learning resources and from e-learnings related to perimeter, area,
volume, surface area, Pythagoras Theorem and Trigonometric ratios. You will be assessed
on your responses with detailed working out to 7 questions.
Instructions for the Student:
This assessment is an individual closed book assessment task. You are not allowed to use
any resources or cheat sheets. This assessment will assess the following topics:
 Perimeter of simple and combined shapes
 Area of simple and combined shapes
 Volume of simple and combined shapes
 Problem solving
 Correct units of measurements
 Pythagoras Theorem
 Trigonometric ratios
The task consists of 7 problem solving questions. To obtain satisfactory for this assessment
you must complete all questions to the standard. You can access the task through the
Content area of VU Collaborate for this unit of competency and selecting Assessment Tasks.
Assessment Location:
This assessment takes place in class time on campus in Week 16. Your teacher will be
supervising while you undertake the test.
Assessment Timing:
This assessment be undertaken in Week 16 during class time and will be open before the
assessment time. You will have 1 hour and 30 minutes to complete all questions in this task.
Resources required for this assessment:
To complete the assessment you will require:
 Access to VU Collaborate
 Internet connection (Note – the internet access is available on campus
through eduroam.)
 A scientific calculator
VET Unit Guide v 5.2 September 2021
Victoria University, RTO Code 3113,
CRICOS Provider No. 00124K (Melb) 02475D (Syd)
22582VIC VU22074 Use arrange of techniques to solve
mathematical problems 1.1 December 2021
Page 1 of 14

 Paper and pen for working out
 You will also require a scanning application such as ‘Genius Scan’
downloaded to your device.
Documents to submit:
The following documents must be uploaded to the drop box for unit VU22074 on the due
date. (Go to ‘Content’, ‘VU22074 Use a range of techniques to solve mathematical
problems’, ‘Assessment Tasks, and ‘Assessment Task 4 Perimeter, area, volume,
Pythagoras Theorem and Trigonometric ratios’). You will need to read and accept the
conditions of assessment.
 This task with all questions completed satisfactorily
 The working out if completed separately
Write your full name and student ID in the space provided on the first page of the
assessment.
Satisfactory completion of the assessment task:
In order to be deemed satisfactory for this assessment you must complete all requirements
as listed in the ‘criteria for satisfactory performance’ table, which you can use to self-assess
your work prior to submission to ensure you have covered all requirements (below).
Resubmission Attempts:
As per the Assessment for Learning – Assessment Procedure (VET) Part G Re-assessment,
you will have two attempts for this assessment task. If you first attempt is unsuccessful your
teacher will give you feedback. Review the feedback and your learning materials before
resubmitting /re-taking the assessment. If you do not demonstrate competence in your
second attempt /submission you should speak with your teacher about the options available
to you.
Assessment Task:
Assessment Task 4
Time allowed: 1 hour and 30 minutes
Perimeter, Area and Volume
(Include formulae, working out and units of measurement in your answers)
(Remember to show your working out)
Answer all questions to 2 decimal places unless specified
Write correct units
Q1. Find the lengths of the missing sides in the following shapes:
VET Unit Guide v 5.2 September 2021
Victoria University, RTO Code 3113,
CRICOS Provider No. 00124K (Melb) 02475D (Syd)
22582VIC VU22074 Use arrange of techniques to solve
mathematical problems 1.1 December 2021
Page 2 of 14

y
x =
x 2m
3m y=
5 m
x = 3 m and y = 5 m as opposite sides of rectangle are equal.
a)
x
x = 5 cm
For calculating y, we need to use Pythagoras Theorem,
i.e.
y2 = 52 – 2.52
y2= 25- 6.25= 21.75
y= 4.33 cm.
b)
Radius =
Radius of circle is half of the diameter. Given that diameter is 2.75 cm, radius is equals to
1.375.
Q1. Using the shapes in Q1 complete the following table:
Shape
Write the name of the
shape
Perimeter
Write correct units
Area
Write correct units
VET Unit Guide v 5.2 September 2021
Victoria University, RTO Code 3113,
CRICOS Provider No. 00124K (Melb) 02475D (Syd)
22582VIC VU22074 Use arrange of techniques to solve
mathematical problems 1.1 December 2021
Page 3 of 14
2.75cm
5cm y

a
Rectangle
Formula: 2 [l +b] where l is
length and b is breadth of
rectangle
Answer:
Perimeter = 2 * [3+5]
Perimeter = 16 m
Formula: l*b
Answer:
Area= 3 * 5= 15m2
b Triangle
Formula: a+b+c
where a, b and c are sides of
the triangle
Answer: Perimeter = 5+5+5 =
15 cm
Formula: 0.5 * base * height
Answer: 0.5 * 5* 4.33
area = 10.82 cm 2
c
circle
Formula: 2* π *r
where r is the radius of circle
Answer:
Given diameter = 2.75 cm
radius r = 1.375 cm
Perimeter = 2 * 3.14 * 1.375
Perimeter = 8.63 cm
Formula: π *r * r
Answer:
Area = 3.14 * 1.375 * 1.375
area = 5.93 cm2
Q3. I’m going to build a vegetable patch in my garden. I’ve decided to make the garden
bed 6 metres long and 2 metres wide.
a) Draw a diagram of the patch below and calculate the perimeter.
Diagram:
6 m
222 2 m
Perimeter:
The vegetable patch will be in shape of rectangle with length 6 meter and width 2 meter.
Perimeter of rectangle = 2 [Length + width]
= 2 * [2+6]
Perimeter = 16 meter
VET Unit Guide v 5.2 September 2021
Victoria University, RTO Code 3113,
CRICOS Provider No. 00124K (Melb) 02475D (Syd)
22582VIC VU22074 Use arrange of techniques to solve
mathematical problems 1.1 December 2021
Page 4 of 14

b) I do not like the sharp edges of my vegetable patch so I have decided to round off
either end with a semi-circle, so that it looks like the diagram below. Calculate the
perimeter of the garden bed now.
(hint: the answer requires more than one step)
Length of rectangular part = 4 m
Diameter of semicircle = 2 m
Radius of semicircle = 1 m
The two semicircles each of diameter 2 meter makes one circle. Thus circumference of circle
is = 2 * 3.14 * r
Perimeter of circle = 2 * 3.14 * 1 = 6.28 m
Total perimeter of new patch = Perimeter of circle + perimeter of two sides of rectangle
= 6.28 + 4 + 4
Perimeter = 14.28 m
VET Unit Guide v 5.2 September 2021
Victoria University, RTO Code 3113,
CRICOS Provider No. 00124K (Melb) 02475D (Syd)
22582VIC VU22074 Use arrange of techniques to solve
mathematical problems 1.1 December 2021
Page 5 of 14

c) If garden edging costs $3.97 per meter and I can only buy it in full meters (ie. round up to
the next metre) how much will it cost me to edge the vegetable patch? Show your working
out.
Unit cost of edging = $3.97 per meter
Perimeter of vegetable patch = 14.28 meter
Thus edging will be purchased for 15 meter. (Rounded off)
Cost of edging vegetable patch = 3.97 * 15 = $ 59.55
d) I now need to dig out the old soil to a depth of 200mm. Calculate the volume of soil
in m3 I need to remove. Show your working out.
Depth = 200 mm = 0.2 m
Given length and width of rectangle are 6 m and 2 m respectively
Volume of rectangle = length * width * depth
Volume = 6 * 2 * 0.2
Volume = 2.4 meter 3
Volume of semi-circle = 0.5 * π r2h
Radius of semi-circle = 1 meter
Volume of semi-circle = 0.5 * 3.14 * 1 *1 * 0.2 = 0.314
As there are two semi-circles so volume of both = 2 * 0.314 = 0.628 meter 3
Total volume = 2.4 + 0.628 = 3.02 meter 3
Volume of soil needed to remove = 3.02 meter 3
e) I am going to line this space with weed matting, calculate the surface area of my
excavated vegetable patch. Show your working out. (Hint: use the perimeter
calculated in part b to find the area of the walls and find the area of the floor)
Surface area for rectangular part- A=2 (wl+ hl+ hw)
= 2*(2*4+0.2*4+0.2*2)
= 18.4 m2
Surface area for circular part-
VET Unit Guide v 5.2 September 2021
Victoria University, RTO Code 3113,
CRICOS Provider No. 00124K (Melb) 02475D (Syd)
22582VIC VU22074 Use arrange of techniques to solve
mathematical problems 1.1 December 2021
Page 6 of 14

A=2πrh+2πr2
=2π * 1 * 0.2+ 2π * 12
=7.53982 m2
Total Surface area= 18.4 + 7.53982 = 25.93982 m2
f) Finally, I will backfill my garden with a mix of composted soil and the excavated soil.
I will use a ratio of three parts composted soil to one part excavated soil. Write this
ratio and then work out how much composted soil I will need.
(Hint: use the volume calculated in part d)
Calculations:
Volume to be filled = 3.02 meter 3
Ratio of composite and excavated soil = 3:1
Thus volume of composite soil which will be needed = [3.02 * 3] /4 = 2.26 m3
VET Unit Guide v 5.2 September 2021
Victoria University, RTO Code 3113,
CRICOS Provider No. 00124K (Melb) 02475D (Syd)
22582VIC VU22074 Use arrange of techniques to solve
mathematical problems 1.1 December 2021
Page 7 of 14

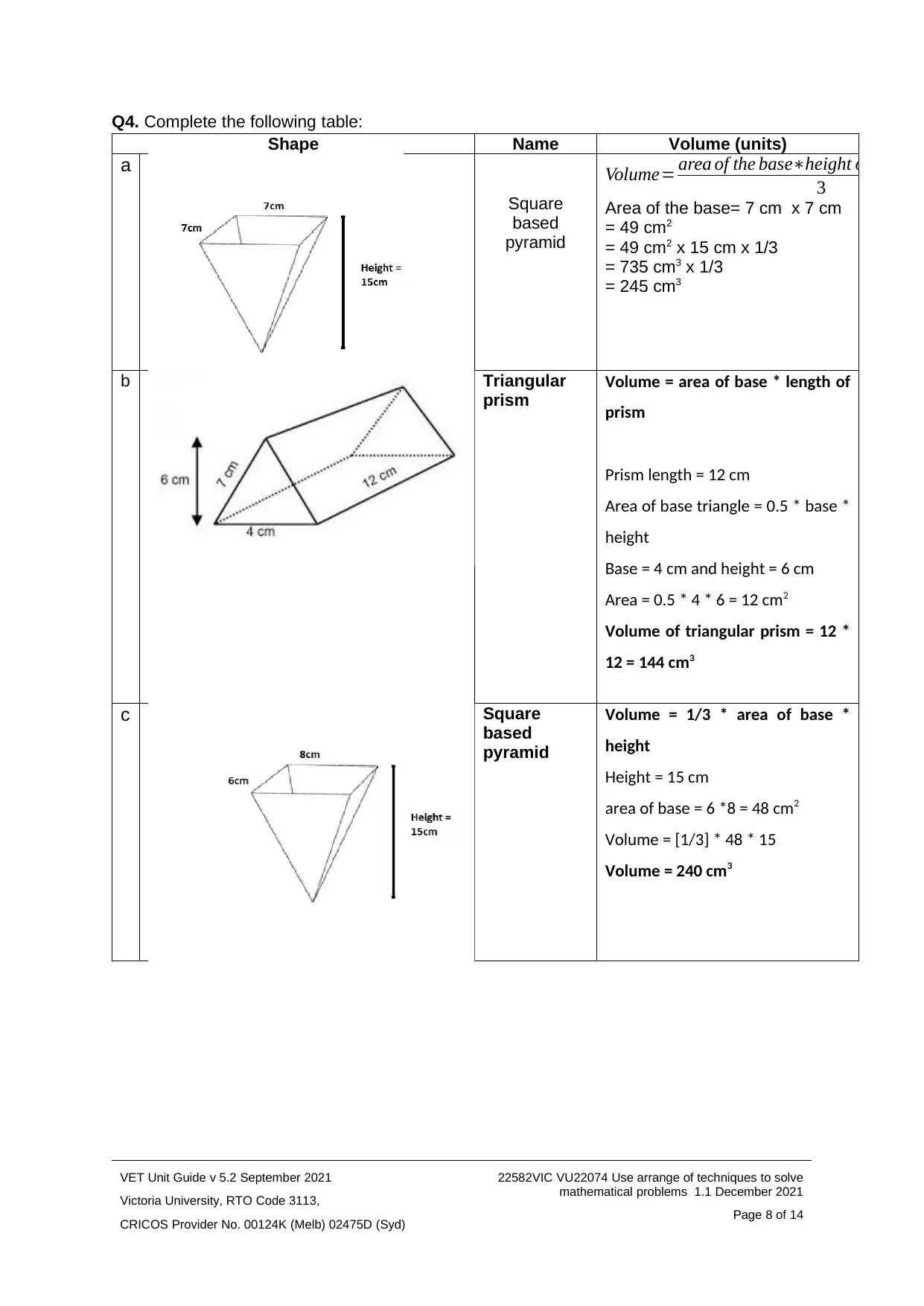
Q4. Complete the following table:
Shape Name Volume (units)
a
Square
based
pyramid
Volume= area of the base∗height of the pyr
3
Area of the base= 7 cm x 7 cm
= 49 cm2
= 49 cm2 x 15 cm x 1/3
= 735 cm3 x 1/3
= 245 cm3
b Triangular
prism
Volume = area of base * length of
prism
Prism length = 12 cm
Area of base triangle = 0.5 * base *
height
Base = 4 cm and height = 6 cm
Area = 0.5 * 4 * 6 = 12 cm2
Volume of triangular prism = 12 *
12 = 144 cm3
c Square
based
pyramid
Volume = 1/3 * area of base *
height
Height = 15 cm
area of base = 6 *8 = 48 cm2
Volume = [1/3] * 48 * 15
Volume = 240 cm3
VET Unit Guide v 5.2 September 2021
Victoria University, RTO Code 3113,
CRICOS Provider No. 00124K (Melb) 02475D (Syd)
22582VIC VU22074 Use arrange of techniques to solve
mathematical problems 1.1 December 2021
Page 8 of 14

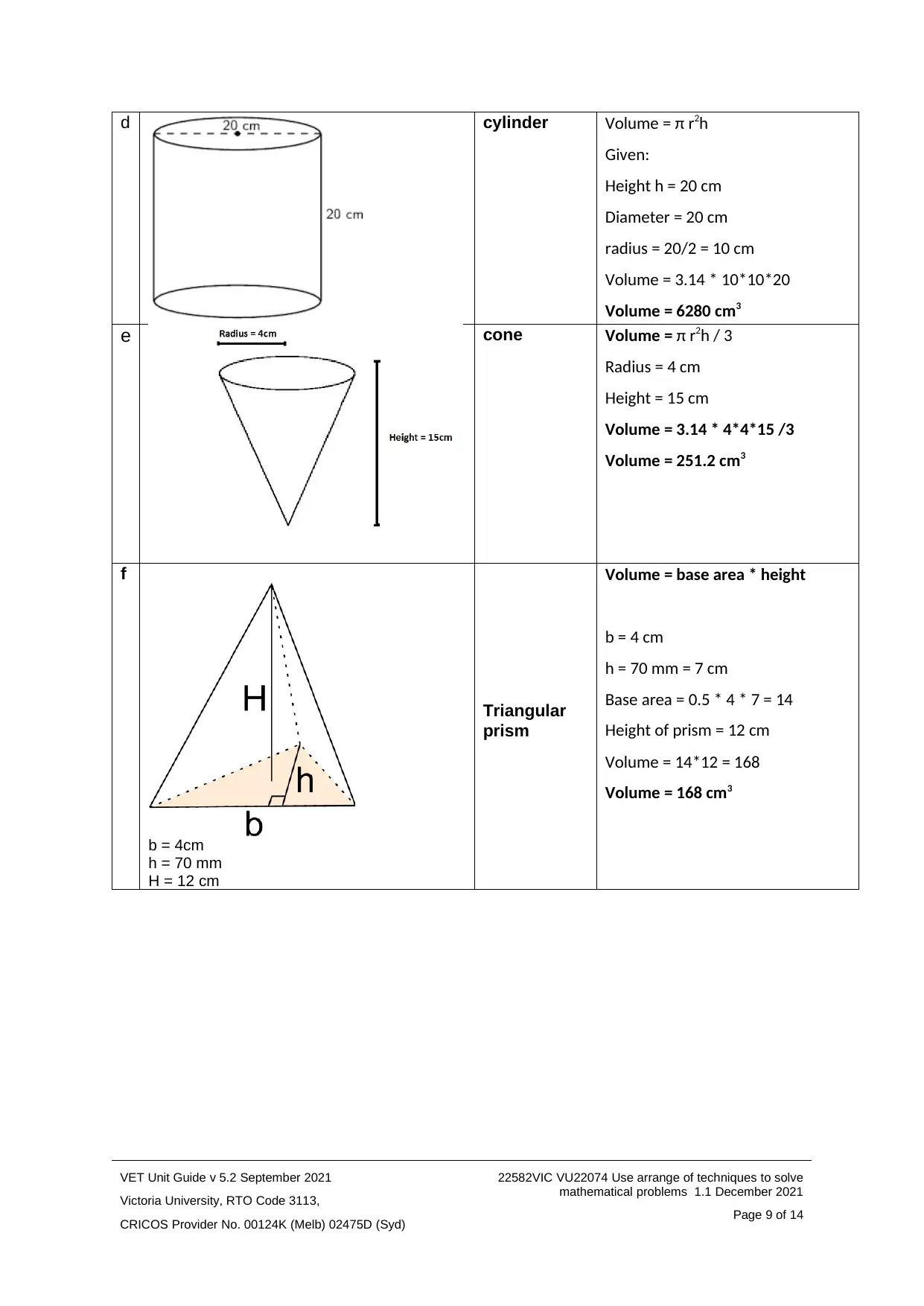
d cylinder Volume = π r2h
Given:
Height h = 20 cm
Diameter = 20 cm
radius = 20/2 = 10 cm
Volume = 3.14 * 10*10*20
Volume = 6280 cm3
e cone Volume = π r2h / 3
Radius = 4 cm
Height = 15 cm
Volume = 3.14 * 4*4*15 /3
Volume = 251.2 cm3
f
b = 4cm
h = 70 mm
H = 12 cm
Triangular
prism
Volume = base area * height
b = 4 cm
h = 70 mm = 7 cm
Base area = 0.5 * 4 * 7 = 14
Height of prism = 12 cm
Volume = 14*12 = 168
Volume = 168 cm3
VET Unit Guide v 5.2 September 2021
Victoria University, RTO Code 3113,
CRICOS Provider No. 00124K (Melb) 02475D (Syd)
22582VIC VU22074 Use arrange of techniques to solve
mathematical problems 1.1 December 2021
Page 9 of 14

Q5. My cat has run up a tree and is stuck. I have a ladder that is 9m long that I lean against
the tree 4m from the base of the trunk so that the top rung is level with where my cat is.
How high up in the tree is my cat? (Draw a diagram to show your working)
Diagram A
B C
Calculations
Height of the tree = AB
Length of ladder AC = 9 m
Distance between base of tree and ladder = BC = 4 m
The arrangement forms a right angle triangle
Using Pythagoras theorem:
AC2 = AB2 + BC2
AB2 = AC2 - BC2
AB2 = 92 - 42
AB2 = 81 – 16
AB2 = 65
AB = 8.06 meter
Thus cat is at height of 8.06 meter
VET Unit Guide v 5.2 September 2021
Victoria University, RTO Code 3113,
CRICOS Provider No. 00124K (Melb) 02475D (Syd)
22582VIC VU22074 Use arrange of techniques to solve
mathematical problems 1.1 December 2021
Page 10 of 14

Q6. Use Pythagoras theorem to find the missing side then use trigonometric ratios
(must use trigonometric ratios) to find the missing angle in the triangle below. How
would you check the answer is correct?
y
i) Find the missing side (either x or y)
Using the law of sines:
8 /sin 25 = x/sin 90
Sin 90 = 1
8 /sin 25 = x
x = 18.95 cm
Using Pythagoras theorem:
x2 = y2 + 82
y2 = (18.95)2 -64
y2= (18.95)2 -64
y2= 295.1
y = 17.17 cm
ii) Find the missing angle (α)
As per trigonometric ratio; in right angle triangle cos x = base / height
From figure it can be seen that:
Cos a = 8 / 18.95
Cos a = 0.422
Angle a = 65.04°
Approximately angle = 65°
VET Unit Guide v 5.2 September 2021
Victoria University, RTO Code 3113,
CRICOS Provider No. 00124K (Melb) 02475D (Syd)
22582VIC VU22074 Use arrange of techniques to solve
mathematical problems 1.1 December 2021
Page 11 of 14
x
8 cm
α
25°

iii) Checking your answer
The answer can be checked by that sum of angles of a triangle is 180. Thus for given
question all three angles are 90, 25 and 65 which sum up to 180 degrees. It proves that
answer is correct.
Q7. Use trigonometric ratios (must use trigonometric ratios) to find the missing
angles in the triangle below. How would you check the answer is correct?
a= 27cm
C
b=32cm
Find missing angle 1
Using Law of Sines,
sin( A)
a = sin ( B)
b =sin (C)
c
VET Unit Guide v 5.2 September 2021
Victoria University, RTO Code 3113,
CRICOS Provider No. 00124K (Melb) 02475D (Syd)
22582VIC VU22074 Use arrange of techniques to solve
mathematical problems 1.1 December 2021
Page 12 of 14
A=76⁰
B

So, sin (76)
27 = sin ( B)
32
= B = sin−1( 32 sin (76)
27 )
B= 42°
Find missing angle 2
C= 180- A+B = 180 – 76 + 42
C= 62°
VET Unit Guide v 5.2 September 2021
Victoria University, RTO Code 3113,
CRICOS Provider No. 00124K (Melb) 02475D (Syd)
22582VIC VU22074 Use arrange of techniques to solve
mathematical problems 1.1 December 2021
Page 13 of 14

Criteria for Satisfactory Performance of the Task
Your teacher will evaluate your work according to the criteria for satisfactory completion of
the task listed below.
If you wish to, you may use the “self-assess” column to evaluate your submission against
each criterion.
ASSESSMENT TASK 4 Self
Assess
1. Find lengths and perimeters of rectangles using appropriate and correct
units
2. Find lengths and perimeters of triangles using appropriate and correct units
3. Find lengths and perimeters of circles using appropriate and correct units
4. Find perimeter of simple combined shapes using appropriate and correct
units
5. Find areas of rectangles using appropriate and correct units
6. Find areas of triangles using appropriate and correct units
7. Find areas of circles using appropriate and correct units
8. Find areas of simple combined shapes using appropriate and correct units
9. Find volumes of prisms and pyramids with rectangular cross-sections with
simple combined shapes using appropriate and correct units
10. Find volumes of prisms and pyramids with triangular cross-sections with
simple combined shapes using appropriate and correct units
11. Find volumes of prisms and pyramids with circular cross-sections with
simple combined shapes using appropriate and correct units
12. Use mathematical symbolism and diagrams to convey mathematical thinking
and processing
13. Convert the unit of a quantity to a unit with a different prefix
14. Find information from a worded problem to solve a problem or analyse
quantitative information
15. Use specialised calculator functions relevant to mathematical needs
16. Use Pythagoras’ Theorem to determine an unknown side of a right-angled
triangle
17. Use Pythagoras’ Theorem and trigonometric ratios to find unknown side
lengths and angles in right-angled triangles
18. Use simple geometry to determine angles in triangles (including non-right
angled)
VET Unit Guide v 5.2 September 2021
Victoria University, RTO Code 3113,
CRICOS Provider No. 00124K (Melb) 02475D (Syd)
22582VIC VU22074 Use arrange of techniques to solve
mathematical problems 1.1 December 2021
Page 14 of 14