Physics: Calculus, Motion, and Optimization Assignment Solutions
VerifiedAdded on 2022/09/01
|11
|1329
|40
Homework Assignment
AI Summary
This document provides detailed solutions to a Physics assignment, covering a range of topics including motion, differentiation, and optimization. The solutions begin with kinematic problems, calculating distance, velocity, and acceleration using the equations of motion and graphical representa...

Physics
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
1.1:- Solution:-
Distance travelled = s in meter
Time Taken = t in sec.
u is the initial velocity = 5 m/s
a is the acceleration = 3 m/s2
t= 10 seconds
Second equation of the motion
S= ut + ½ a t2……………….(1)
On putting the value of u, a and t in equation (1) we can calculate the distance in meter.
S= 5 x 10 +1/2(3 x(10 x 10))
S=5 x 10 + ½ (300)
S= 50 + 150
S= 200 meters
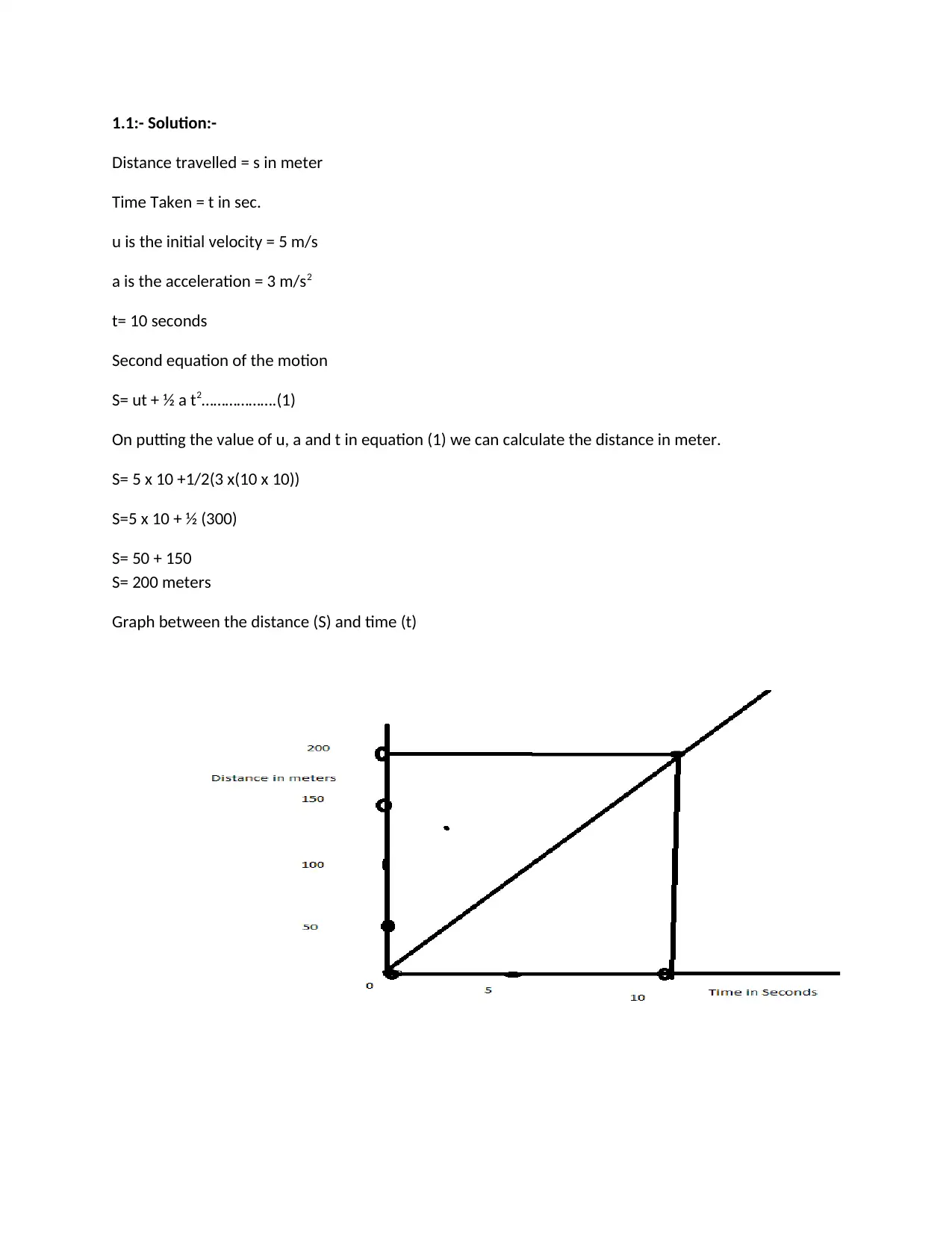
Graph between the distance (S) and time (t)
Distance travelled = s in meter
Time Taken = t in sec.
u is the initial velocity = 5 m/s
a is the acceleration = 3 m/s2
t= 10 seconds
Second equation of the motion
S= ut + ½ a t2……………….(1)
On putting the value of u, a and t in equation (1) we can calculate the distance in meter.
S= 5 x 10 +1/2(3 x(10 x 10))
S=5 x 10 + ½ (300)
S= 50 + 150
S= 200 meters
Graph between the distance (S) and time (t)
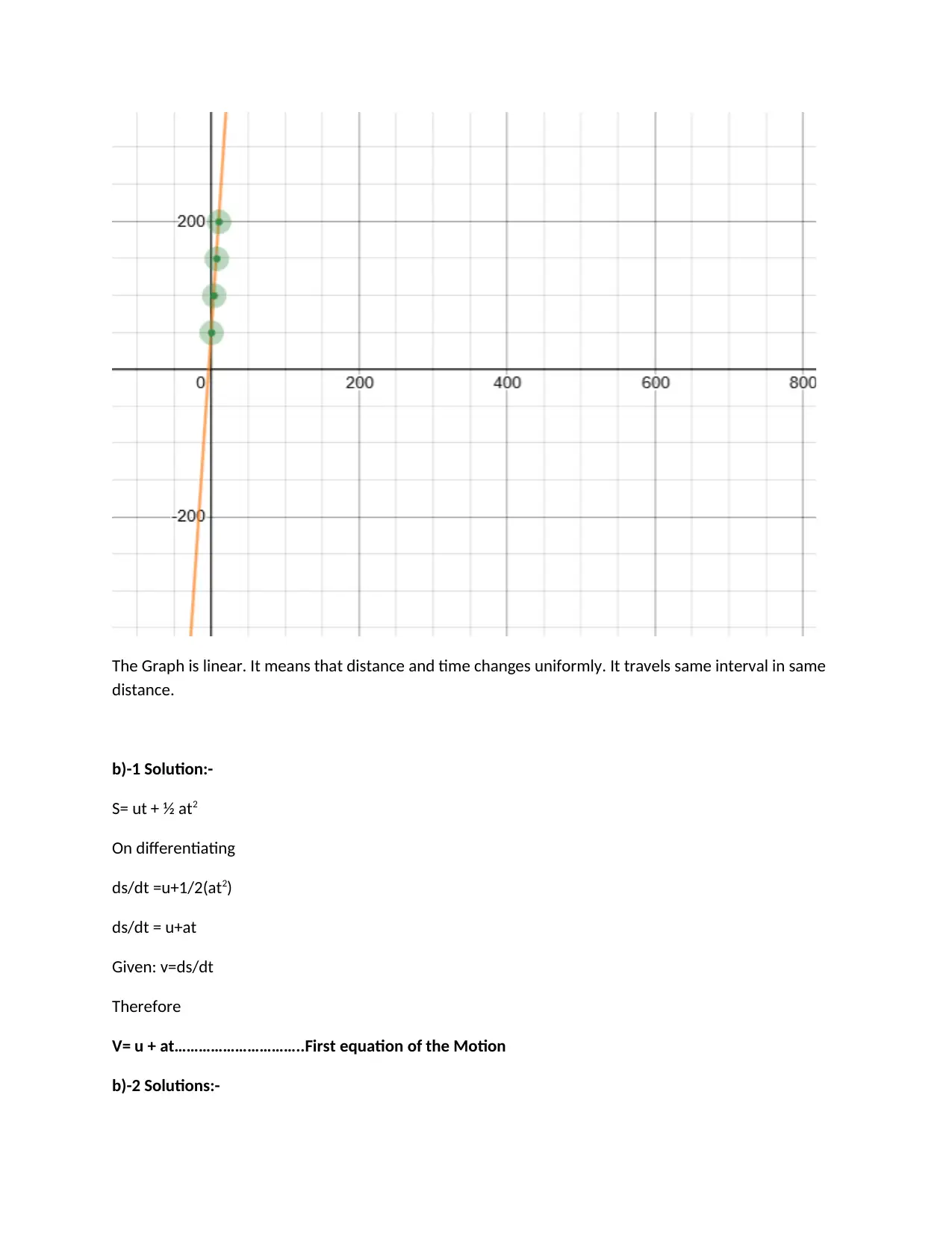
The Graph is linear. It means that distance and time changes uniformly. It travels same interval in same
distance.
b)-1 Solution:-
S= ut + ½ at2
On differentiating
ds/dt =u+1/2(at2)
ds/dt = u+at
Given: v=ds/dt
Therefore
V= u + at…………………………..First equation of the Motion
b)-2 Solutions:-
distance.
b)-1 Solution:-
S= ut + ½ at2
On differentiating
ds/dt =u+1/2(at2)
ds/dt = u+at
Given: v=ds/dt
Therefore
V= u + at…………………………..First equation of the Motion
b)-2 Solutions:-
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

a =dv/dt …….given
a =dv/dt= d2s/dt2
a= dv/dt = d/dt (u+at)
On differentiating
It becomes
dv/dt= d/dt (0+a)
a=acceleration
1.3 Solutions:-
u is the initial velocity = 5 m/s
a is the acceleration = 3 m/s2
for calculate the value velocity
at t= 10 seconds
by using ist equation of the motion
v= u + at…………………………….(2)
On putting the value in equation (2)
We obtained
V= 5 + 3 x 10
V= 5+30
V= 35 m/s
Acceleration (a) change in velocity/time
From the above graph
a= (Final velocity – initial velocity)/time
Final velocity= 35m/s
Initial velocity = 3 m/s
a= (35-3)/10
a =dv/dt= d2s/dt2
a= dv/dt = d/dt (u+at)
On differentiating
It becomes
dv/dt= d/dt (0+a)
a=acceleration
1.3 Solutions:-
u is the initial velocity = 5 m/s
a is the acceleration = 3 m/s2
for calculate the value velocity
at t= 10 seconds
by using ist equation of the motion
v= u + at…………………………….(2)
On putting the value in equation (2)
We obtained
V= 5 + 3 x 10
V= 5+30
V= 35 m/s
Acceleration (a) change in velocity/time
From the above graph
a= (Final velocity – initial velocity)/time
Final velocity= 35m/s
Initial velocity = 3 m/s
a= (35-3)/10
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

a=3.2 m/s2
2 Solutions:-
Displacement of mass = y= 2x2+4x3
Steps to find the turning Points:-
Step 1:- find dy/dx
Step 2:- set dy/dx=0 solve for x values
Step 3:-Substitute the value of x in the original y= f(x) and get value of y
Step 4:-Write in form (x,y)
y= 2x2+4x3
On differentiating
It becomes
dy/dx= 4x+12x2
4x=-12x2
x=-1/3
Substitute the value of x in the original y= f(x)
y= 2(1/3)2+4(1/3)3
y= 2/9-4/27
y=2/27
Turning points: (x, y) = (-1/3, 2/27)
3 Solutions:-
Equation for the Charging of Capacitor
V= v0 e-t/T …………………………………(4)
T= is Time constant of the circuit equal to RC
2 Solutions:-
Displacement of mass = y= 2x2+4x3
Steps to find the turning Points:-
Step 1:- find dy/dx
Step 2:- set dy/dx=0 solve for x values
Step 3:-Substitute the value of x in the original y= f(x) and get value of y
Step 4:-Write in form (x,y)
y= 2x2+4x3
On differentiating
It becomes
dy/dx= 4x+12x2
4x=-12x2
x=-1/3
Substitute the value of x in the original y= f(x)
y= 2(1/3)2+4(1/3)3
y= 2/9-4/27
y=2/27
Turning points: (x, y) = (-1/3, 2/27)
3 Solutions:-
Equation for the Charging of Capacitor
V= v0 e-t/T …………………………………(4)
T= is Time constant of the circuit equal to RC

R – Resistance of the circuit
C- Capacitor of the Circuit
v0- Initial voltage
V0 = 11
For t1 = 3 sec
On putting the value of t1 in equation (4)we obtained
V= v0 e-3/T
By using chain rule
dv/dt = v0 d/dt e-3/T + e-3/T d/dt v0
Differentiation of constant term is zero
dv/dt = v0 d/dt e-3/T
dv/dt = 11 (-1) e1/T
For t1 = 5 sec
V= v0 e-5/T
By using chain rule
dv/dt = v0 d/dt e-5/T + e-5/T d/dt v0
Differentiation of constant term is zero
dv/dt = v0 d/dt e-5/T
dv/dt = 11(-1) e1/T
(b) Second derivative
dv/dt = v0 (-1) e1/T
On differentiating again
d2v/dt2=0
C- Capacitor of the Circuit
v0- Initial voltage
V0 = 11
For t1 = 3 sec
On putting the value of t1 in equation (4)we obtained
V= v0 e-3/T
By using chain rule
dv/dt = v0 d/dt e-3/T + e-3/T d/dt v0
Differentiation of constant term is zero
dv/dt = v0 d/dt e-3/T
dv/dt = 11 (-1) e1/T
For t1 = 5 sec
V= v0 e-5/T
By using chain rule
dv/dt = v0 d/dt e-5/T + e-5/T d/dt v0
Differentiation of constant term is zero
dv/dt = v0 d/dt e-5/T
dv/dt = 11(-1) e1/T
(b) Second derivative
dv/dt = v0 (-1) e1/T
On differentiating again
d2v/dt2=0
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

4 Solutions:-
(a) V = 12(1- e-t/2 )
On differentiating
dv/dt = 12- 12e-t/2
dv/dt = 0 – 12(-1) e-t/2
dv/dt = 0 – 12(-1) e1/2
e1/2 = 1.6487
dv/dt = 12 x 1.6487
dv/dt = 19.784
(b) When t= 5 sec
dv/dt = 12- 12e-t/2
dv/dt = 12e-5/2
dv/dt = 12 x 12.18
dv/dt = 146.18
When t= 3sec
dv/dt = 12- 12e-t/2
dv/dt = 12e3/2
dv/dt = 12 x 4.481
dv/dt = 53.78
(c) Second derivative of dv/dt
dv/dt = 0 – 12(-1) e-1/2
d2v/dt2= 12
5 Solutions:-
(a) V = 12(1- e-t/2 )
On differentiating
dv/dt = 12- 12e-t/2
dv/dt = 0 – 12(-1) e-t/2
dv/dt = 0 – 12(-1) e1/2
e1/2 = 1.6487
dv/dt = 12 x 1.6487
dv/dt = 19.784
(b) When t= 5 sec
dv/dt = 12- 12e-t/2
dv/dt = 12e-5/2
dv/dt = 12 x 12.18
dv/dt = 146.18
When t= 3sec
dv/dt = 12- 12e-t/2
dv/dt = 12e3/2
dv/dt = 12 x 4.481
dv/dt = 53.78
(c) Second derivative of dv/dt
dv/dt = 0 – 12(-1) e-1/2
d2v/dt2= 12
5 Solutions:-
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

d/dx logax = 1/x [Ln(a)]
Assumption: log is equal to log10
By using the Chain Rule
d/dt (u,v) =- u*dv/dt+ v*du/dt
G = 20 log10V
a) dG/dV = [20/ [10V ln 10)] x10
= 20 / (V ln 10)
dG/dV = 20 / (V ln 10)
b) d2G/dV2= ( 20 / ln 10 )(-1/ v2)
= -20 (20 /ln 10 )/v2
d2G/dV2= -20 (20 /ln 10 )/v2
6 Solutions:-
Y= 2e-t sin3t
Product rule for differentiation: d/dt (u,v) =- u*dv/dt+ v*du/dt
V=dy/dt = 2[e-t sin3t]
V=dy/dt =2{[e-t d/dt(sin3t)]+ sin3t d/dt (e-t)}
V=dy/dt = 2 [e-t x3x (cos3t) + sin 3t (-1) e-t )
V=dy/dt = 2[3 e-t cos3t – e-t sin 3t]
V=dy/dt = 6 e-t cos 3t – 2 e-t sin3t
7 Solutions:-
Velocity v= (2t+3)4
By chain rule d/dt (u,v) =- u*dv/dt+ v*du/dt
v= (2t+3)4 *1
Assumption: log is equal to log10
By using the Chain Rule
d/dt (u,v) =- u*dv/dt+ v*du/dt
G = 20 log10V
a) dG/dV = [20/ [10V ln 10)] x10
= 20 / (V ln 10)
dG/dV = 20 / (V ln 10)
b) d2G/dV2= ( 20 / ln 10 )(-1/ v2)
= -20 (20 /ln 10 )/v2
d2G/dV2= -20 (20 /ln 10 )/v2
6 Solutions:-
Y= 2e-t sin3t
Product rule for differentiation: d/dt (u,v) =- u*dv/dt+ v*du/dt
V=dy/dt = 2[e-t sin3t]
V=dy/dt =2{[e-t d/dt(sin3t)]+ sin3t d/dt (e-t)}
V=dy/dt = 2 [e-t x3x (cos3t) + sin 3t (-1) e-t )
V=dy/dt = 2[3 e-t cos3t – e-t sin 3t]
V=dy/dt = 6 e-t cos 3t – 2 e-t sin3t
7 Solutions:-
Velocity v= (2t+3)4
By chain rule d/dt (u,v) =- u*dv/dt+ v*du/dt
v= (2t+3)4 *1

dv/dt = 4(2t+ 3)3 +d/dt (2t+3)
dv/dt = 8 (2t +3)3
a=d/dt (dv/dt)
Therefore
a=d/dt (dv/dt) = 8 x 3(2t+3)2 d/dt (2t+3)
= 24 (2t+3)2 x 2
= 48 (2t + 3)2
= 48 (4t2 +12t +9)
a=d/dt (dv/dt) = 48 (4t2 +12t +9)
8 Solutions:-
Y = sint/t
By chain rule d/dt (u,v) =- u*dv/dt+ v*du/dt
Y = (t)-1 sint
U= (t)-1 and v= sint
On differentiating
It becomes
dy/dt = (t)-1 cost + sint (-1)t-2
dy/dt = cost/t- sint /t2
dy/dt =(tcost –sint)/t2
dy/dt =(tcost –sint)/t2
9 Solutions:-
Perimeter = 2 (l + b)
Perimeter = 2 (l + b) = 750
(l + b) = 375
dv/dt = 8 (2t +3)3
a=d/dt (dv/dt)
Therefore
a=d/dt (dv/dt) = 8 x 3(2t+3)2 d/dt (2t+3)
= 24 (2t+3)2 x 2
= 48 (2t + 3)2
= 48 (4t2 +12t +9)
a=d/dt (dv/dt) = 48 (4t2 +12t +9)
8 Solutions:-
Y = sint/t
By chain rule d/dt (u,v) =- u*dv/dt+ v*du/dt
Y = (t)-1 sint
U= (t)-1 and v= sint
On differentiating
It becomes
dy/dt = (t)-1 cost + sint (-1)t-2
dy/dt = cost/t- sint /t2
dy/dt =(tcost –sint)/t2
dy/dt =(tcost –sint)/t2
9 Solutions:-
Perimeter = 2 (l + b)
Perimeter = 2 (l + b) = 750
(l + b) = 375
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

l= x
Therefore
b= (375 – x)
Area will be Maximum when dA /dx= 375-2X=0
2x = 375
x= 375/2
A = 375 x 375/4
A= 35, 156.251 m2
10 Solutions:-
Squares cut from the corners are x×x inches
Open-top box height = x mm
Width of 12−2h mm
length = 120 mm
New length = 120-2x mm
Width = 140 mm
New Width = 140 -2x mm
so it's volume will be
V(x) = x (120−2x) (140−2x) mm3
On solving above equation it becomes
V(x) =x (120x -2x)(140-2x)
V(x) =x (120 (140-2x) -2x (140 -2x))
V(x) =x (16800 -24 x – 280 x +4x2)
V(x) =x (4 x2 – 304 x -16800)
V(x) = 4x3 -304x2 -16800
Therefore
b= (375 – x)
Area will be Maximum when dA /dx= 375-2X=0
2x = 375
x= 375/2
A = 375 x 375/4
A= 35, 156.251 m2
10 Solutions:-
Squares cut from the corners are x×x inches
Open-top box height = x mm
Width of 12−2h mm
length = 120 mm
New length = 120-2x mm
Width = 140 mm
New Width = 140 -2x mm
so it's volume will be
V(x) = x (120−2x) (140−2x) mm3
On solving above equation it becomes
V(x) =x (120x -2x)(140-2x)
V(x) =x (120 (140-2x) -2x (140 -2x))
V(x) =x (16800 -24 x – 280 x +4x2)
V(x) =x (4 x2 – 304 x -16800)
V(x) = 4x3 -304x2 -16800
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

Critical points occur when the derivative (dv/dx) is equal to zero.
Therefore dv/dx =0
dv/dx = 12x2-608x
dv/dx = x (12x- 608)
dv/dx = 4x (3x-152)
x= 50.6666
x=51 mm
(b) So its volume will be
x= 51mm would result in widths and lengths of zero, and therefore a volume of zero), so it is obviously
not the critical point for the maximum.
(c) Therefore the maximum volume is achieved by cutting out squares that are
51 x 51 inches from the corners of the larger sheet.
Therefore dv/dx =0
dv/dx = 12x2-608x
dv/dx = x (12x- 608)
dv/dx = 4x (3x-152)
x= 50.6666
x=51 mm
(b) So its volume will be
x= 51mm would result in widths and lengths of zero, and therefore a volume of zero), so it is obviously
not the critical point for the maximum.
(c) Therefore the maximum volume is achieved by cutting out squares that are
51 x 51 inches from the corners of the larger sheet.
1 out of 11
Related Documents
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
© 2024 | Zucol Services PVT LTD | All rights reserved.





