Interpreting Negative Values in Velocity-Time Graphs

The physics assignment involves multiple sections focusing on different aspects of physical principles. The first section presents experimental results for determining the metal's toughness and compares the Young’s Modulus to textbook values. In the second part, calculations are carried out to find ...Read More

Physics Assignment
Student Name:
University
8th January 8, 2018

Q1:
Solution
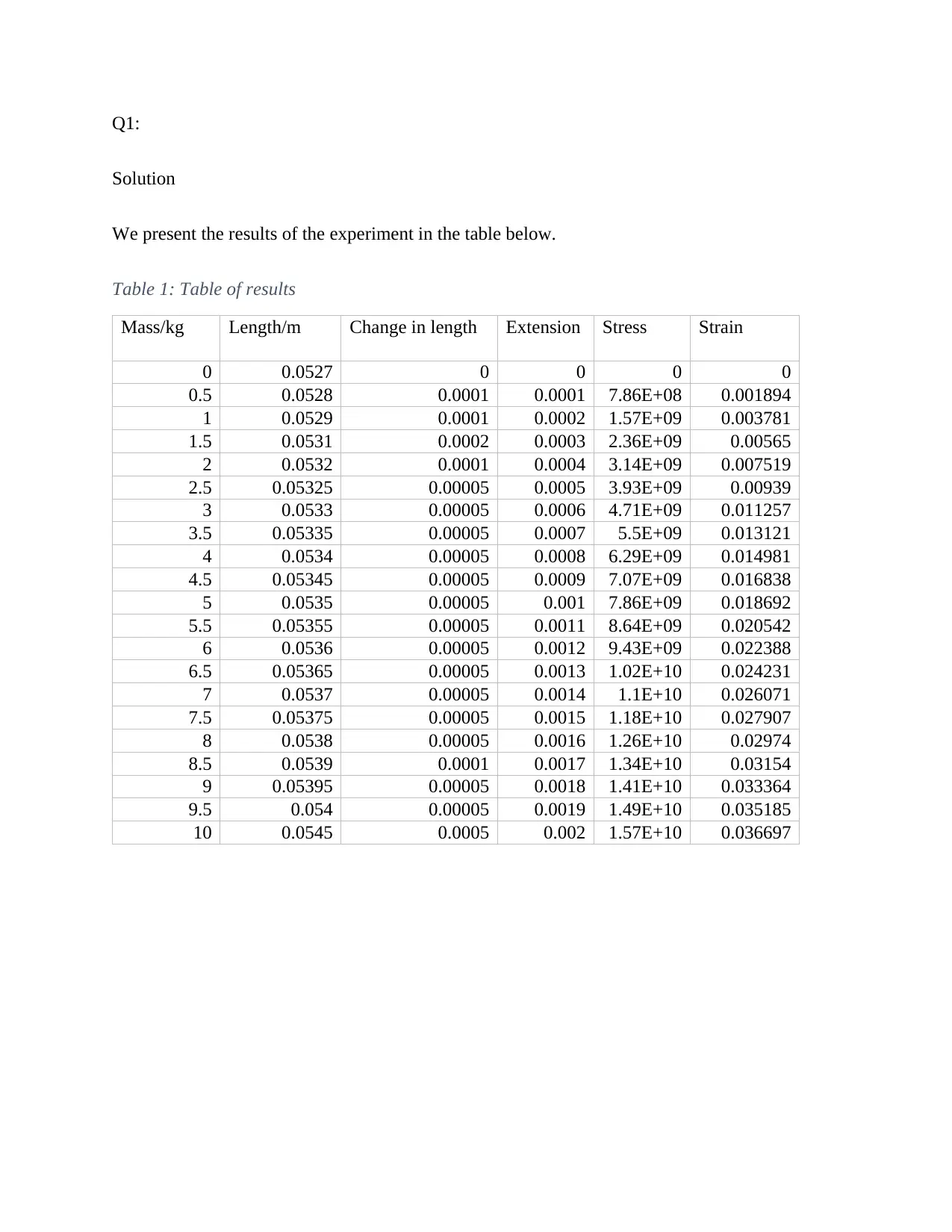
We present the results of the experiment in the table below.
Table 1: Table of results
Mass/kg Length/m Change in length Extension Stress Strain
0 0.0527 0 0 0 0
0.5 0.0528 0.0001 0.0001 7.86E+08 0.001894
1 0.0529 0.0001 0.0002 1.57E+09 0.003781
1.5 0.0531 0.0002 0.0003 2.36E+09 0.00565
2 0.0532 0.0001 0.0004 3.14E+09 0.007519
2.5 0.05325 0.00005 0.0005 3.93E+09 0.00939
3 0.0533 0.00005 0.0006 4.71E+09 0.011257
3.5 0.05335 0.00005 0.0007 5.5E+09 0.013121
4 0.0534 0.00005 0.0008 6.29E+09 0.014981
4.5 0.05345 0.00005 0.0009 7.07E+09 0.016838
5 0.0535 0.00005 0.001 7.86E+09 0.018692
5.5 0.05355 0.00005 0.0011 8.64E+09 0.020542
6 0.0536 0.00005 0.0012 9.43E+09 0.022388
6.5 0.05365 0.00005 0.0013 1.02E+10 0.024231
7 0.0537 0.00005 0.0014 1.1E+10 0.026071
7.5 0.05375 0.00005 0.0015 1.18E+10 0.027907
8 0.0538 0.00005 0.0016 1.26E+10 0.02974
8.5 0.0539 0.0001 0.0017 1.34E+10 0.03154
9 0.05395 0.00005 0.0018 1.41E+10 0.033364
9.5 0.054 0.00005 0.0019 1.49E+10 0.035185
10 0.0545 0.0005 0.002 1.57E+10 0.036697

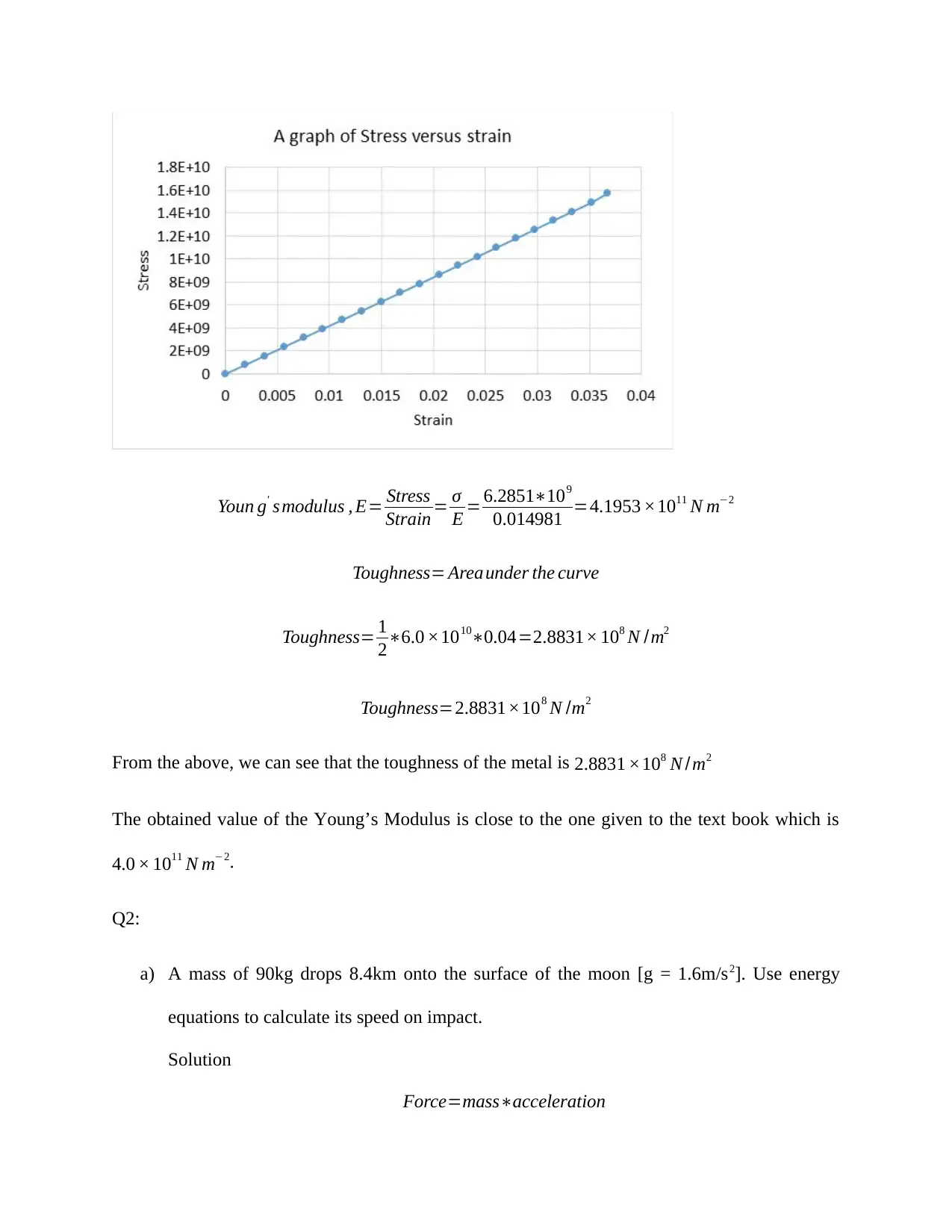
Youn g' s modulus , E= Stress
Strain = σ
E = 6.2851∗109
0.014981 =4.1953 ×1011 N m−2
Toughness= Areaunder the curve
Toughness= 1
2∗6.0 ×1010∗0.04=2.8831× 108 N /m2
Toughness=2.8831×108 N /m2
From the above, we can see that the toughness of the metal is 2.8831 ×108 N /m2
The obtained value of the Young’s Modulus is close to the one given to the text book which is
4.0 × 1011 N m−2.
Q2:
a) A mass of 90kg drops 8.4km onto the surface of the moon [g = 1.6m/s2]. Use energy
equations to calculate its speed on impact.
Solution
Force=mass∗acceleration

Force=90∗1.6=144 N
Kinetic energy ( KE )=Force∗distance=144∗8400=1,209,600 Joules
But again
KE=m× v2
v2= KE
m
v= √ KE
m = √ 1209600
90 = √ 13440=115.9310 m/ s
b) Use ‘suvat’ to check your answer to part a).
Solution
S=Distance
U=Initial velocity
V=Velocity to be solved
A=Acceleration
T=Time
s= 1
2 a t2
t2= 2 s
a
t= √ 2 s
a = √ 2∗8400
1.6 = √ 10500
s= 1
2 ( u+v ) t
s= 1
2 ( u+v ) t
8400=1
2 ( 0+v )∗√ 10500

16800=v∗ √10500
v= 16800
√ 10500
c) How long does it take to land?
Solution
s= 1
2 a t2
t2= 2 s
a
t= √ 2 s
a = √ 2∗8400
1.6 = √ 10500=102.5 seconds
d) What assumptions have you made in parts a), b) and c)?
Solution
One of the assumptions is that the initial velocity is zero
Q2: Experiment

Figure 1: Single Shear
Figure 2: Double shear
Shear Modulus
It is the ratio of shear stress and shear strain of the material.
Load (N) Dial Gauge Reading (mm) Deflection (mm)
0 0 0

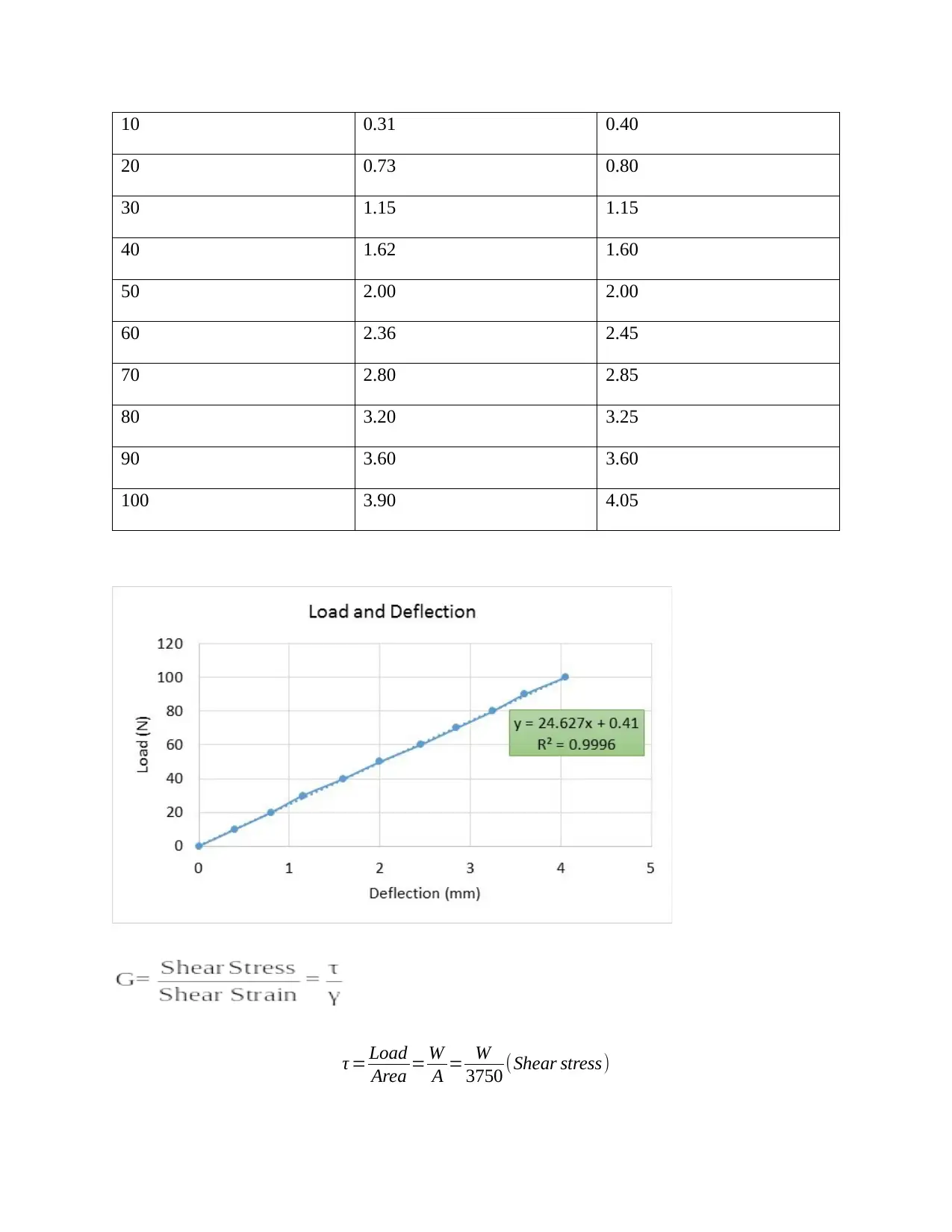
10 0.31 0.40
20 0.73 0.80
30 1.15 1.15
40 1.62 1.60
50 2.00 2.00
60 2.36 2.45
70 2.80 2.85
80 3.20 3.25
90 3.60 3.60
100 3.90 4.05
τ = Load
Area = W
A = W
3750 (Shear stress)

γ= δ
b = δ
75 (Strain angle)
G=
W
3750∗75
8 =
75
3750∗1
graph gradient ¿
Slope = Graph Gradient = 24.627, W
True Value = 0 .46 MPA
G= slope∗W
A = 24.627∗75
3750 =0.49254
Error= |0.46−0.49254|
0.46 ∗100 %=7.07 %
Errors founded and may be affected on a results in the experiment due to many reasons listed
below:
 Zero error: If the dial gauge’s reading isn’t zero at zero load.
 Human error: if the experimenter red the dial gauge and calculate incorrectly.
Q3:
Below is a velocity-time graph for a car
a) Without doing any calculations, how can you tell when the car had its greatest
acceleration?
Solution
One can tell by looking at the shape of the graph. The car had its greatest acceleration
where the graph is very steep.

b) Calculate the acceleration during the first 100s
Solution
Acceleration=Change∈ velocity
Change∈time = 22
100 =0.22 m/ s2
c) Calculate how far the car travels while decelerating
Solution
d= v2
2 a
v=initial velocity=30 m/ s
a= Change∈velocity
Change∈time = 30
300 =0.1 m/s2
d= v2
2 a = 302
2∗0.1= 900
0.2 =4500 m
d) Calculate the total displacement of the car at the end of the journey
Solution
Total displacement= Area under the curve
Total displacement= ( 1
2∗22∗100 )+ ( 22∗200 )+ ( 1
2 ( 22+30 )∗100 )+ ( 1
2∗30∗300 )=1100+4400+2600+ 4500
Q4:
a) The graph below shows a different car journey. What do the negative y-values
indicate?
Solution
The negative y-values indicate negative velocity which implies that the car is moving
in a negative direction
b) Calculate the total distance travelled.
Solution

Total distance travelled=Area of the graph
Total distance travelled=( 1
2∗30∗200 )+ ( 1
2∗10∗100 )=3000+500=3500 m
c) Calculate the displacement at the end of the journey
Solution
Displacement at the end of the journey= ( 1
2∗30∗200 ) −( 1
2∗10∗100 ) =3000−500=2500 m