Physics 201 Lab 1 - Working with Numbers

Learn how to determine the acceleration of gravity on an unknown planet by making a plot of position vs time using LoggerPro software. Fit a quadratic equation and calculate the acceleration due to gravity.

Physics 201
Lab 1 – Working with Numbers Name Christian Fay
Anything that you type must be highlighted in order to distinguish your writing from the original text. Do not edit
any of the text in this document. Just type your answers under the appropriate question. You must submit all Logger
Pro (.cmbl) files with your report. Please delete any videos within the .cmbl file before saving it and submitting it.
This is a word document and you can type your answer directly into the lab for submission. You will need to
download and install LoggerPro to do this lab. Instructions for doing this are available in Blackboard. Please follow
the directions for doing this carefully. All students are required to have access to a computer which can access and
open all course material.
Read the articles on Measurements and Graphing and Fitting Data. Also read, print out and keep handy the
papers on Principle Formulas and Some Useful Information. Please make sure you follow the directions for each
problem carefully.
1. After completing this lab, be sure to take the online quiz on Blackboard under Lab 01. Do not take this quiz
until you have read the material above. You will have only one chance to complete it.
2. You will submit this completed in lab in Blackboard at the same location that you downloaded it from.
3. Use the Logger Pro software to make a plot of the position vs time given in the following table. You are an
astronaut on an unknown planet. You want to determine the acceleration of gravity on this planet so you go
to top of a high cliff and drop a rock over the edge. The dependent variable is the position and the
independent variable is the time. The table below is the measured position of a rock as it falls from the top
of the cliff. The rock obeys the kinematic equation y = vot + ½ gt2 where g represents the acceleration due to
gravity. Make a plot of the data in LoggerPro and making sure you label the plot properly.
Measurement Position (m) Time (s)
1 0 0.0
2 26.8 1.00
3 60.3 2.00
4 107. 3.00
5 168. 4.00
6 241. 5.00
7 328. 6.00
8 429. 7.00
9 543. 8.00
10 670. 9.00
2024-08-30

Physics 201
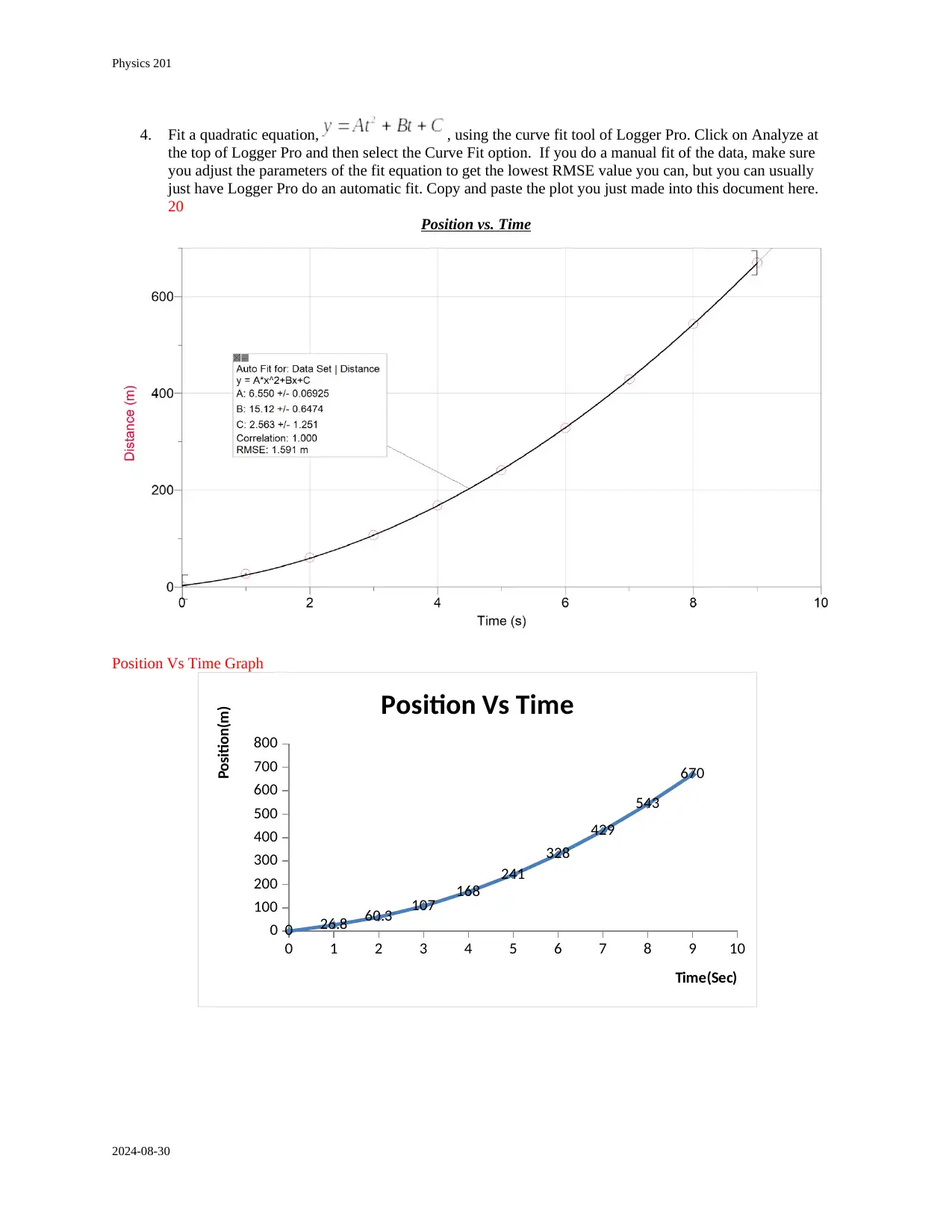
4. Fit a quadratic equation, , using the curve fit tool of Logger Pro. Click on Analyze at
the top of Logger Pro and then select the Curve Fit option. If you do a manual fit of the data, make sure
you adjust the parameters of the fit equation to get the lowest RMSE value you can, but you can usually
just have Logger Pro do an automatic fit. Copy and paste the plot you just made into this document here.
20
Position vs. Time
Position Vs Time Graph
0 1 2 3 4 5 6 7 8 9 10
0
100
200
300
400
500
600
700
800
0 26.8 60.3 107 168
241
328
429
543
670
Position Vs Time
Time(Sec)
Position(m)
2024-08-30

Physics 201
5. Compare the kinematics equation governing the motion and the format of the fit equation that you just
made to explain how you can use the coefficients (either A, B, or C) to calculate the acceleration due to
gravity. 13 pts
The theory, the kinematic equation y = vot + ½ gt2, predicates the object’s position as a function of time and
can be calculated. The theoretical curve is parabolic. The measured values and plotted graph also produce
a parabolic curve.
Both the “theory equation” and the “fit equation” are quadratic equations and share the same form of Y =
A*t^2+B*t+ C.
Both describe a falling object under gravity’s constant acceleration. The coefficient used in theory to
describe acceleration, initial velocity, and initial position would be the same coefficients used in the “fit
equation.” Coefficient “A” = ½*g and describes the acceleration of gravity. “B” would become the
object’s initial velocity, and “C” describes the initial position
By comparing kinematic equation with quadratic equation “A” is half of acceleration due to gravity “g”.
To find acceleration due to gravity “g” finds coefficient “A” “B” and “C” by using position and time
values.
6. Identify the coefficients of your fit equation. 5 pts
A = 6.550
B =15.12
C = 2.563
7. Calculate “g” for the unknown planet using the method described in question 5. 12 pts
Quadric equation
Y =6.550t2 +15.12t +2.56 3
Kinematic Equation
Y =V 0 t + 1
2 g t 2
Now comparing both equation 1
2 g=6.550∧V 0=15.12 so acceleration due to gravity
g=2× 6.55=13.1 m/ s2
Acceleration due to gravity of unknown planet is 13.1 m/s2
2024-08-30