S217 Physics: Classical to Quantum Mechanics - TMA 01 Solved Paper
VerifiedAdded on 2023/06/12
|5
|960
|123
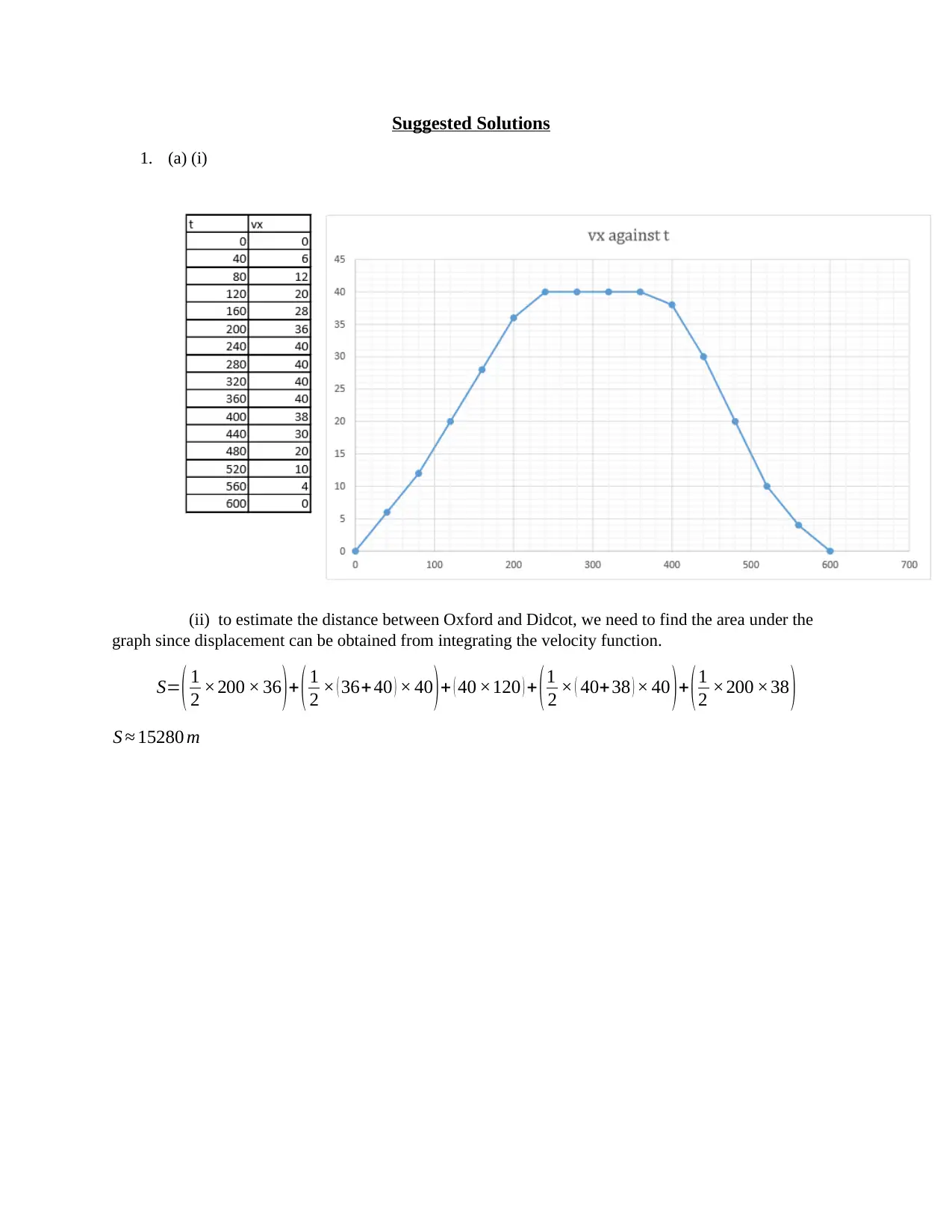
Homework Assignment
AI Summary
This document presents solutions to a Physics assignment focusing on concepts from classical to quantum mechanics. The assignment covers topics such as estimating distance using velocity functions, projectile motion including calculations of time of flight and maximum height, Kepler's laws of planetary motion, simple harmonic motion including calculations of maximum velocity and acceleration, and resultant forces. Detailed calculations and explanations are provided for each question, demonstrating the application of physics principles. Desklib is a valuable resource for students, offering a wide range of solved assignments and past papers to support their learning.
1 out of 5






![[object Object]](/_next/static/media/star-bottom.7253800d.svg)