Physics Solution
VerifiedAdded on 2023/04/08
|13
|1775
|424
AI Summary
This document provides detailed solutions for various physics problems and equations. It covers topics such as Newton's laws of motion, momentum, collisions, forces, equations of motion, and more. The solutions are explained step-by-step, making it easier for students to understand and apply the concepts. Whether you need help with homework or want to improve your understanding of physics, this document is a valuable resource.
Contribute Materials
Your contribution can guide someone’s learning journey. Share your
documents today.

PHYSICS SOLUTION
Student Name
Institution Affiliation
Instructor’s Name
Course Name
Date
Student Name
Institution Affiliation
Instructor’s Name
Course Name
Date
Secure Best Marks with AI Grader
Need help grading? Try our AI Grader for instant feedback on your assignments.

1. a) State Isaac Newton’s three laws of motion
Law 1
It states that a body is in its state of rest or uniform motion unless an unbalanced force acts on it.
Law 2
It states that the rate of change of momentum of a body is proportional to the applied force and
takes place in the direction in which the force acts.
Law 3
It states that for every action or force, there is an equal and opposite force or reaction.
2. a) What is the formula for momentum and what are the units for momentum?
Momentum= velocity*mass.
Momentum=vm ; where v is the velocity and m is the mass
The SI units for momentum is kgm/s
b) What is meant by conservation of momentum?
Conservation of linear momentum refers to a situation when the total momentum of the
system stays constant when no outside forces act on a system of moving objects.
c) A gas molecule of mass 5*10- 2 6 kg travelling at 320m/s strikes the side of a
container perpendicularly. The collision is elastic. What is meant by elastic
collision?
Elastic collision occurs when bodies collide and bounce off each other after
collision. In elastic collision, both momentum and kinetic energy are conserved.
d) Use the information in part c to calculate the change in momentum of the
molecule during its collision with the side of the container.
Change in momentum= mv-mu
= (0)-(5*10 - 2 6 kg*320m/s) kgm/s
=-1.6*10 - 2 3 kgm/s
3. A racing car moving at 25m/s collides with a wall . The driver of mass 65kg is
brought to rest by its seatbelt in 0.2s. Find:
a) The driver’s change in momentum
Change in momentum=mv-mu; where v is the final velocity, u is initial velocity
=Since the driver is brought to rest,
v=0m/s and u=25m/s
= (0m/s*65kg)-(25m/s*65kg)
= (0-1625)kgm/s
=-1625kgm/s
Law 1
It states that a body is in its state of rest or uniform motion unless an unbalanced force acts on it.
Law 2
It states that the rate of change of momentum of a body is proportional to the applied force and
takes place in the direction in which the force acts.
Law 3
It states that for every action or force, there is an equal and opposite force or reaction.
2. a) What is the formula for momentum and what are the units for momentum?
Momentum= velocity*mass.
Momentum=vm ; where v is the velocity and m is the mass
The SI units for momentum is kgm/s
b) What is meant by conservation of momentum?
Conservation of linear momentum refers to a situation when the total momentum of the
system stays constant when no outside forces act on a system of moving objects.
c) A gas molecule of mass 5*10- 2 6 kg travelling at 320m/s strikes the side of a
container perpendicularly. The collision is elastic. What is meant by elastic
collision?
Elastic collision occurs when bodies collide and bounce off each other after
collision. In elastic collision, both momentum and kinetic energy are conserved.
d) Use the information in part c to calculate the change in momentum of the
molecule during its collision with the side of the container.
Change in momentum= mv-mu
= (0)-(5*10 - 2 6 kg*320m/s) kgm/s
=-1.6*10 - 2 3 kgm/s
3. A racing car moving at 25m/s collides with a wall . The driver of mass 65kg is
brought to rest by its seatbelt in 0.2s. Find:
a) The driver’s change in momentum
Change in momentum=mv-mu; where v is the final velocity, u is initial velocity
=Since the driver is brought to rest,
v=0m/s and u=25m/s
= (0m/s*65kg)-(25m/s*65kg)
= (0-1625)kgm/s
=-1625kgm/s

b) The average force exerted by the seatbelt on the driver?
F=ma
a = v
t
= 25 m/s
0.2 s
=125ms- 2
Since it was a deceleration, a=-125ms - 2
F=ma
=-125ms- 2 * 65Kg
=-8125N. The negative sign illustrates it was a retardation.
c) How many times is this force greater than the driver’s weight?
Weight=mg
g=10N/kg
Driver’s weight= 65kg *10N/kg
=650N
Comparing with retardation force
= 8125
650
=12.5 times greater
4. a) i. What is happening to the speed of the ball bearing between points A and B?
The speed is increasing uniformly from point A to B.
ii. Explain in terms of forces X and Y why this happens.
Here, force X acts on the ball bearing uniformly i.e. the magnitude of force X is
higher than that of Y between these points and thus X acts on the ball bearing uniformly
pulling it down at an increasing speed.
iii. What is happening to the speed of the ball between C and D?
Between point C and D, the speed of the ball is constant.
iv) Explain in terms of forces X and Y why this happens.
The speed between C and D is constant because the magnitude of both forces X and Y are
constant.
F=ma
a = v
t
= 25 m/s
0.2 s
=125ms- 2
Since it was a deceleration, a=-125ms - 2
F=ma
=-125ms- 2 * 65Kg
=-8125N. The negative sign illustrates it was a retardation.
c) How many times is this force greater than the driver’s weight?
Weight=mg
g=10N/kg
Driver’s weight= 65kg *10N/kg
=650N
Comparing with retardation force
= 8125
650
=12.5 times greater
4. a) i. What is happening to the speed of the ball bearing between points A and B?
The speed is increasing uniformly from point A to B.
ii. Explain in terms of forces X and Y why this happens.
Here, force X acts on the ball bearing uniformly i.e. the magnitude of force X is
higher than that of Y between these points and thus X acts on the ball bearing uniformly
pulling it down at an increasing speed.
iii. What is happening to the speed of the ball between C and D?
Between point C and D, the speed of the ball is constant.
iv) Explain in terms of forces X and Y why this happens.
The speed between C and D is constant because the magnitude of both forces X and Y are
constant.

b) Use the graph to help you calculate the distance travelled by the ball bearing between
points C and D.
There was no change in velocity between the two points and thus V is constant
V= 2.4cm/s
Time taken, t= (4-2) s
=2s
Distance=V * t
=2.4cm/s*2s
=4.8cm
5. a) Define the term resultant force?
A resultant force is a force obtained by combining all the magnitudes of the forces acting on a
body taking into consideration their directions to obtain a single force.
b) Two force vectors each have magnitude of 12 newton. When they are added together
which of the following magnitudes of the resultant vector could not be produced? Circle
your answer
The answer is 30N
c) Sketch 3 vector diagrams below to show how the other three resultant vectors could
be produced.
0N
12N 24N
d) Find the resultant magnitude and angle from the horizontal of a Force 7 N East
followed by a force of 9 N North
Magnitude=√ (F12 + F22)
=√ (92 + 72)
=√ (81+49)
=√130
=11.4 N
Angle =tan-1 Fy
Fx
=tan-1( 9
7 )
=tan-1 1.286
=52.13o
points C and D.
There was no change in velocity between the two points and thus V is constant
V= 2.4cm/s
Time taken, t= (4-2) s
=2s
Distance=V * t
=2.4cm/s*2s
=4.8cm
5. a) Define the term resultant force?
A resultant force is a force obtained by combining all the magnitudes of the forces acting on a
body taking into consideration their directions to obtain a single force.
b) Two force vectors each have magnitude of 12 newton. When they are added together
which of the following magnitudes of the resultant vector could not be produced? Circle
your answer
The answer is 30N
c) Sketch 3 vector diagrams below to show how the other three resultant vectors could
be produced.
0N
12N 24N
d) Find the resultant magnitude and angle from the horizontal of a Force 7 N East
followed by a force of 9 N North
Magnitude=√ (F12 + F22)
=√ (92 + 72)
=√ (81+49)
=√130
=11.4 N
Angle =tan-1 Fy
Fx
=tan-1( 9
7 )
=tan-1 1.286
=52.13o
Secure Best Marks with AI Grader
Need help grading? Try our AI Grader for instant feedback on your assignments.

6. a) There are several equations of motions which can be used to study the dynamics of
objects. One is given below.
V= u +at
Name each of the terms in the formula and give their correct units.
v is the final velocity. Its units is ms-1
u is the initial velocity. Its units is ms-1
a is the acceleration. Its units is given by ms-2
t is the time taken. Its units is s.
b) A ball is dropped from a height of 6m and falls vertically to the ground. Find its velocity
just before hitting the ground. Neglect air resistance.
=v2=u +gs
s=6m
u =0 m/s
g= 10m/s2
v2=0+10ms-2*6m
v2=60m2s-2
v=√(60m2s-2)
v=7.75m/s
c).A Newcastle United footballer kicks a ball so that it leaves his boot at an angle of 35
degrees from horizontal with a velocity of 18m/s. Determine whether it will reach a
defender 30 m away without bouncing. Neglect air resistance.
Time taken to reach maximum height is given as, t=u/g
Where u is the initial velocity while g=10m/s2
t= u
g = 18 m/ s
10 m/ s 2
t=1.8s
Maximum height reached=u2 /2g
=324/20
=16.2m
Time of flight =2t
=2*1.8s
=3.6s
Distance taken to reach maximum height =ut
objects. One is given below.
V= u +at
Name each of the terms in the formula and give their correct units.
v is the final velocity. Its units is ms-1
u is the initial velocity. Its units is ms-1
a is the acceleration. Its units is given by ms-2
t is the time taken. Its units is s.
b) A ball is dropped from a height of 6m and falls vertically to the ground. Find its velocity
just before hitting the ground. Neglect air resistance.
=v2=u +gs
s=6m
u =0 m/s
g= 10m/s2
v2=0+10ms-2*6m
v2=60m2s-2
v=√(60m2s-2)
v=7.75m/s
c).A Newcastle United footballer kicks a ball so that it leaves his boot at an angle of 35
degrees from horizontal with a velocity of 18m/s. Determine whether it will reach a
defender 30 m away without bouncing. Neglect air resistance.
Time taken to reach maximum height is given as, t=u/g
Where u is the initial velocity while g=10m/s2
t= u
g = 18 m/ s
10 m/ s 2
t=1.8s
Maximum height reached=u2 /2g
=324/20
=16.2m
Time of flight =2t
=2*1.8s
=3.6s
Distance taken to reach maximum height =ut

=18m/s*1.8s
=32.4
From Pythagoras theorem, a2=b2+c2
32.42 =16.22 +c2
c2=32.42-16.22
c2 =787.32
c=28.06m
The distance taken before bouncing is 2c=2*28.06
=56.12 m
7. a) State the principle of moments
It states that when a body is in balance or in equilibrium, the sum of the clockwise
moments equals the sum of anti-clockwise moments.
b) If the mass of the beam is 20kg, calculate the magnitude of force W.
Anticlockwise moments = clockwise moments
20kg *10N/kg=200N
Anticlockwise moments=weight *Distance
=200N*1m
=200Nm
200Nm=w*1m
w=200N
c).Calculate the magnitude of forces A and B
The magnitude of A is 200N since it is equal to w
Magnitude of B= sum of downward forces is equal to sum of upward force
=200N +200N
=400N
d).What name is given to force B?
Pivot
8. a) On graph paper, plot a graph of distance against time using the data given
below.
Time(s) Distance(m)
0 0
=32.4
From Pythagoras theorem, a2=b2+c2
32.42 =16.22 +c2
c2=32.42-16.22
c2 =787.32
c=28.06m
The distance taken before bouncing is 2c=2*28.06
=56.12 m
7. a) State the principle of moments
It states that when a body is in balance or in equilibrium, the sum of the clockwise
moments equals the sum of anti-clockwise moments.
b) If the mass of the beam is 20kg, calculate the magnitude of force W.
Anticlockwise moments = clockwise moments
20kg *10N/kg=200N
Anticlockwise moments=weight *Distance
=200N*1m
=200Nm
200Nm=w*1m
w=200N
c).Calculate the magnitude of forces A and B
The magnitude of A is 200N since it is equal to w
Magnitude of B= sum of downward forces is equal to sum of upward force
=200N +200N
=400N
d).What name is given to force B?
Pivot
8. a) On graph paper, plot a graph of distance against time using the data given
below.
Time(s) Distance(m)
0 0
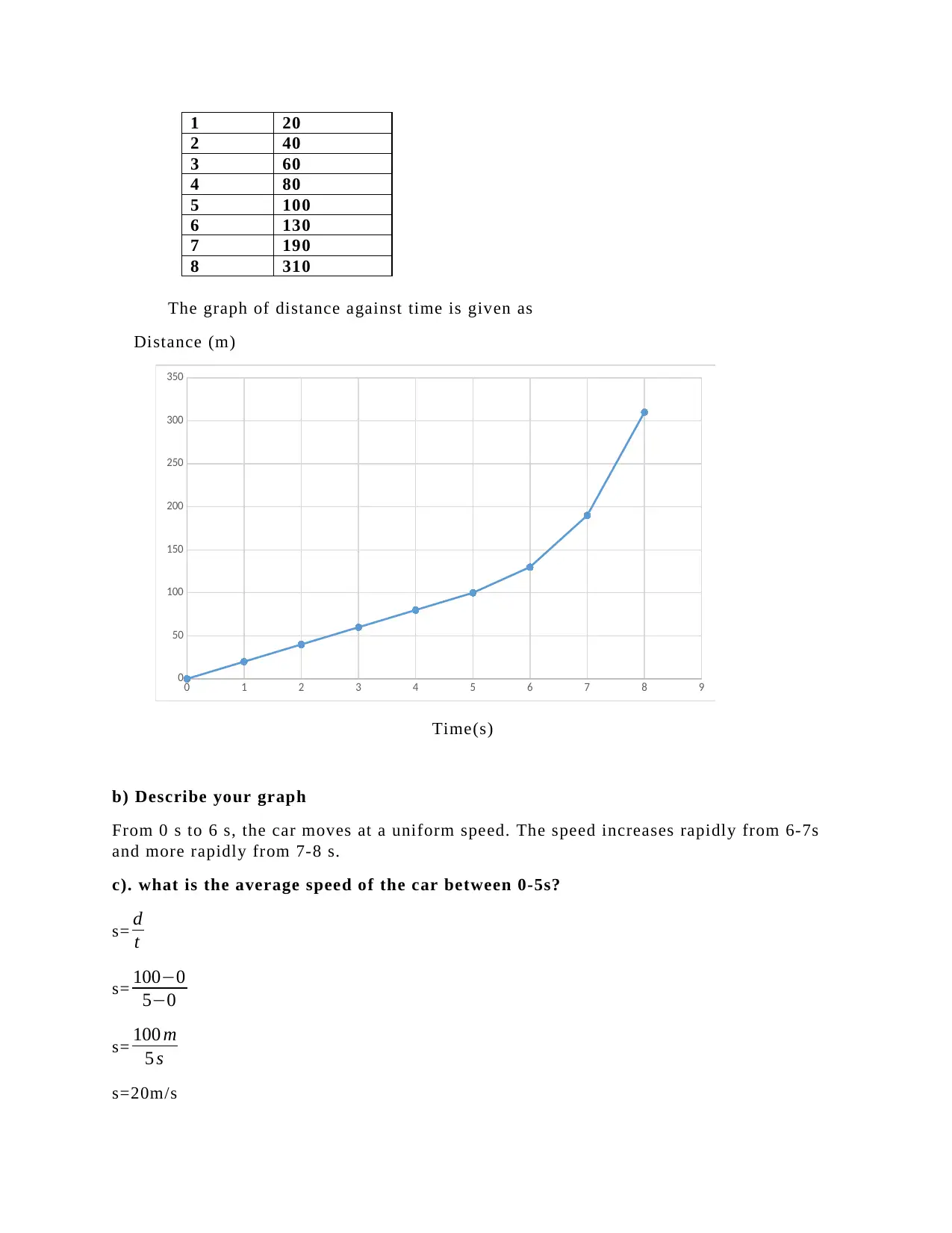
1 20
2 40
3 60
4 80
5 100
6 130
7 190
8 310
The graph of distance against time is given as
Distance (m)
0 1 2 3 4 5 6 7 8 9
0
50
100
150
200
250
300
350
Time(s)
b) Describe your graph
From 0 s to 6 s, the car moves at a uniform speed. The speed increases rapidly from 6-7s
and more rapidly from 7-8 s.
c). what is the average speed of the car between 0-5s?
s= d
t
s= 100−0
5−0
s= 100 m
5 s
s=20m/s
2 40
3 60
4 80
5 100
6 130
7 190
8 310
The graph of distance against time is given as
Distance (m)
0 1 2 3 4 5 6 7 8 9
0
50
100
150
200
250
300
350
Time(s)
b) Describe your graph
From 0 s to 6 s, the car moves at a uniform speed. The speed increases rapidly from 6-7s
and more rapidly from 7-8 s.
c). what is the average speed of the car between 0-5s?
s= d
t
s= 100−0
5−0
s= 100 m
5 s
s=20m/s
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

d).What is the average speed of the car for the whole journey?
s= d
t
s= 310−0
8−0
s= 310 m
8 s
s= 38.75m/s
e). Use your graph to calculate how long it took a car to cover a distance of 240m.
From the graph, time taken to cover 240 m is 7.5 s
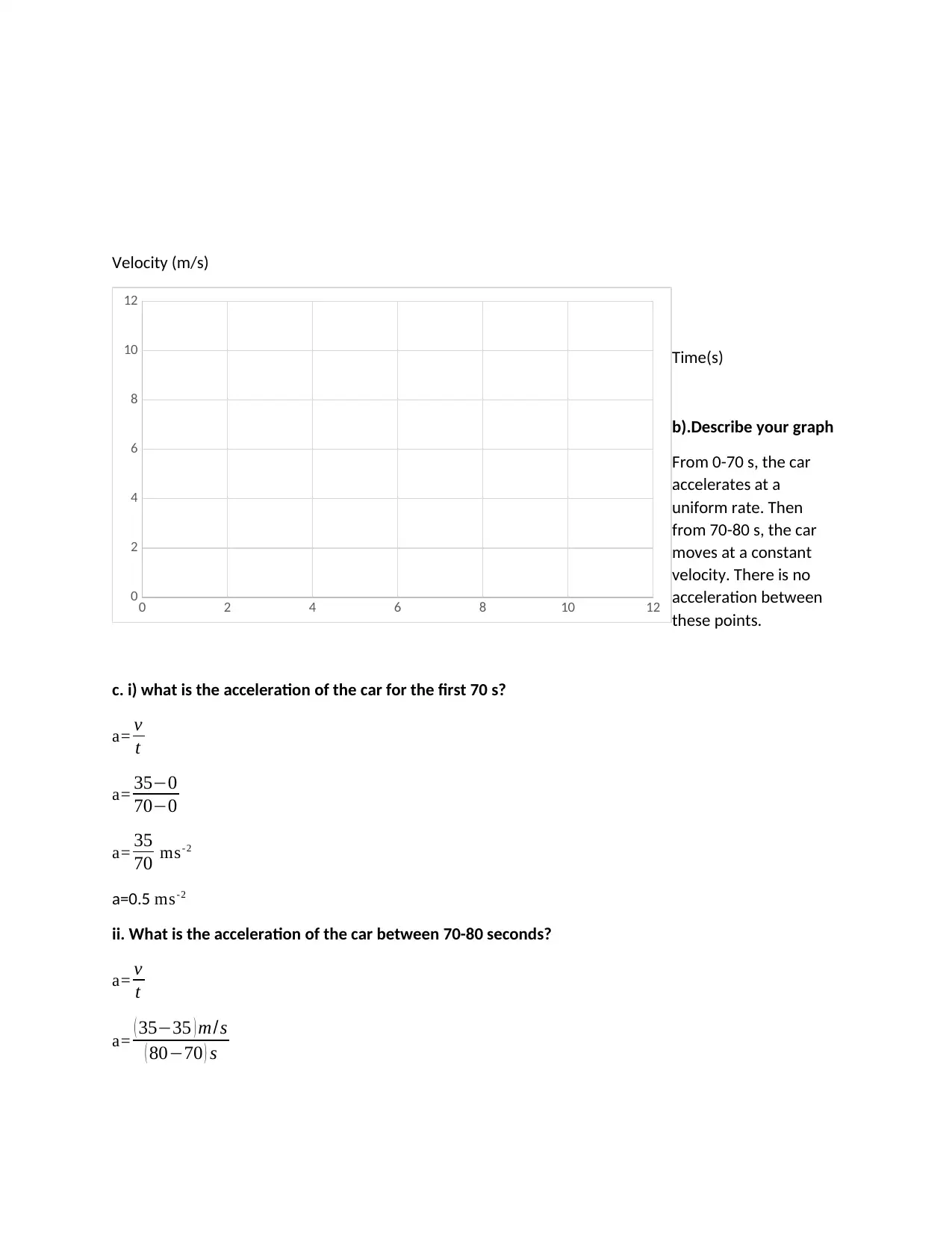
9. a). Use the graph paper to plot a graph of velocity against time using the date shown for the
car journey.
Time(s) Velocity(m/s)
0 0
10 5
20 10
30 15
40 20
50 25
60 30
70 35
80 35
The graph of velocity against time will be given as
s= d
t
s= 310−0
8−0
s= 310 m
8 s
s= 38.75m/s
e). Use your graph to calculate how long it took a car to cover a distance of 240m.
From the graph, time taken to cover 240 m is 7.5 s
9. a). Use the graph paper to plot a graph of velocity against time using the date shown for the
car journey.
Time(s) Velocity(m/s)
0 0
10 5
20 10
30 15
40 20
50 25
60 30
70 35
80 35
The graph of velocity against time will be given as
Velocity (m/s)
Time(s)
b).Describe your graph
From 0-70 s, the car
accelerates at a
uniform rate. Then
from 70-80 s, the car
moves at a constant
velocity. There is no
acceleration between
these points.
c. i) what is the acceleration of the car for the first 70 s?
a= v
t
a= 35−0
70−0
a= 35
70 ms- 2
a=0.5 ms- 2
ii. What is the acceleration of the car between 70-80 seconds?
a= v
t
a= ( 35−35 ) m/s
( 80−70 ) s
0 2 4 6 8 10 12
0
2
4
6
8
10
12
Time(s)
b).Describe your graph
From 0-70 s, the car
accelerates at a
uniform rate. Then
from 70-80 s, the car
moves at a constant
velocity. There is no
acceleration between
these points.
c. i) what is the acceleration of the car for the first 70 s?
a= v
t
a= 35−0
70−0
a= 35
70 ms- 2
a=0.5 ms- 2
ii. What is the acceleration of the car between 70-80 seconds?
a= v
t
a= ( 35−35 ) m/s
( 80−70 ) s
0 2 4 6 8 10 12
0
2
4
6
8
10
12

a= 0
10 ms- 2
a=0 ms- 2
iii. Use your graph to calculate how far the car travelled in 80 s
Distance covered is equivalent to the area under the curve
The area under the curve forms a triangle for the first 70 s and a rectangle between 70 and
80s
Area of triangle = 1
2b*h
=¿*70*35) m
=1225m
Area of rectangle=l*w
= (10*35) m
=350m
Total distance travelled =1225m +350m
=1575 m
10. A car is travelling towards some traffic lights at 15m/s when the driver sees the
light change to red. It takes the driver 2.0 s to react, and the car decelerates on
braking at a rate of -7.5 ms- 2 .
a).Calculate:
i).The distance the car travels before the driver reacts.
Distance, s=v*t
=15m/s*2s
=30m
ii).The distance travelled whilst the brakes are applied.
a= -7.5ms- 2
v= 15m/s
Time taken to bring the car to rest =t = v
a
t= 15 m/ s
7.5 ms−2
10 ms- 2
a=0 ms- 2
iii. Use your graph to calculate how far the car travelled in 80 s
Distance covered is equivalent to the area under the curve
The area under the curve forms a triangle for the first 70 s and a rectangle between 70 and
80s
Area of triangle = 1
2b*h
=¿*70*35) m
=1225m
Area of rectangle=l*w
= (10*35) m
=350m
Total distance travelled =1225m +350m
=1575 m
10. A car is travelling towards some traffic lights at 15m/s when the driver sees the
light change to red. It takes the driver 2.0 s to react, and the car decelerates on
braking at a rate of -7.5 ms- 2 .
a).Calculate:
i).The distance the car travels before the driver reacts.
Distance, s=v*t
=15m/s*2s
=30m
ii).The distance travelled whilst the brakes are applied.
a= -7.5ms- 2
v= 15m/s
Time taken to bring the car to rest =t = v
a
t= 15 m/ s
7.5 ms−2
Secure Best Marks with AI Grader
Need help grading? Try our AI Grader for instant feedback on your assignments.

t=2s
Distance travelled= 1
2v*t
= 1
2*15m/s*2s
=15m
iii).The total stopping distance.
The total distance =Distance before the driver reacts + Distance whilst the brakes are
applied
The total distance =30m + 15m
=45m
iv).The time taken to stop once the driver has started to brake.
t= v
a
t= 15 m/ s
7.5 ms−2
t=2s
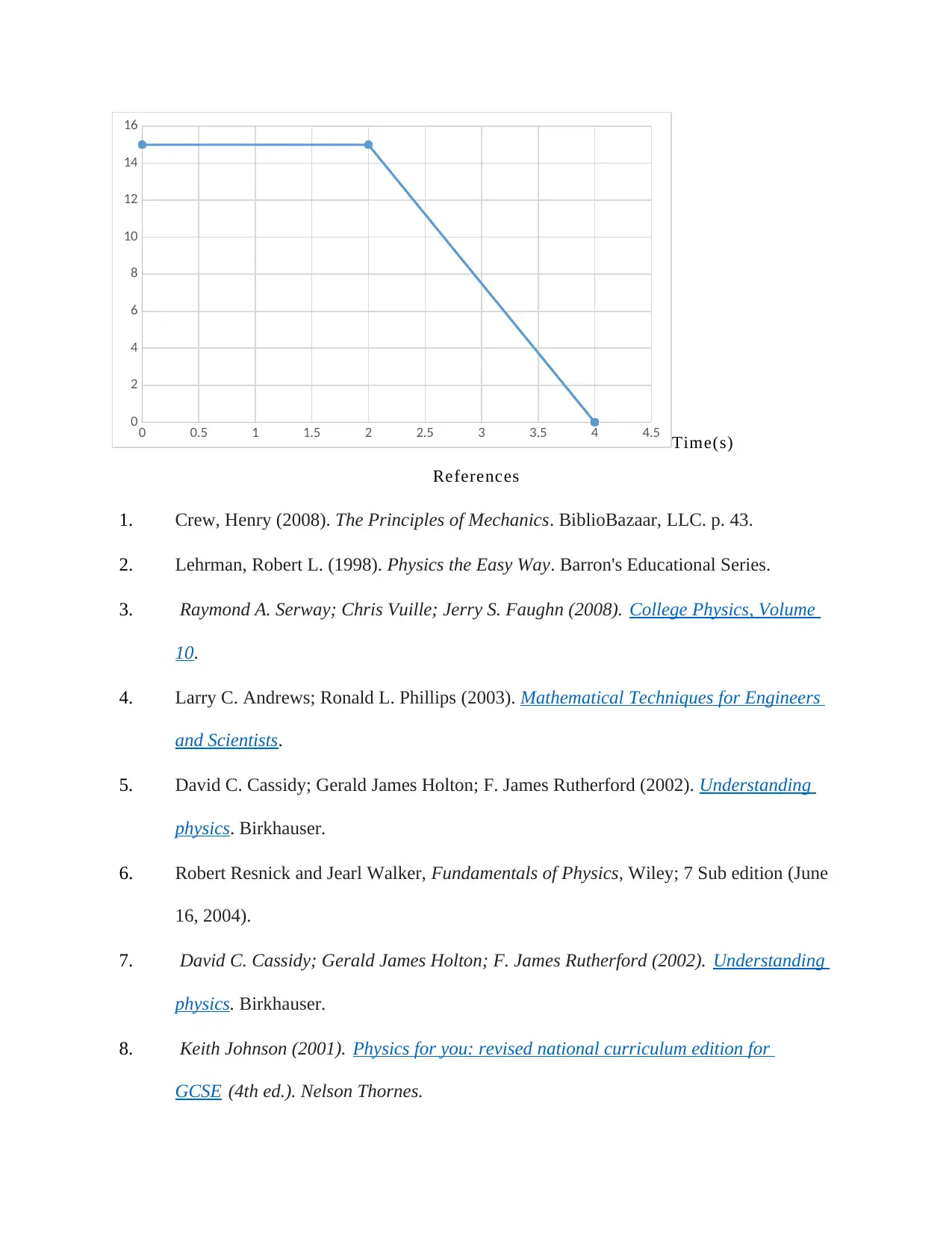
b). In the space below, sketch a velocity-time graph to represent this event.
The following are the data obtained
Time(s) Velocity(m/s)
0 15
2 15
4 0
The graph is given as:
Velocity (m/s)
Distance travelled= 1
2v*t
= 1
2*15m/s*2s
=15m
iii).The total stopping distance.
The total distance =Distance before the driver reacts + Distance whilst the brakes are
applied
The total distance =30m + 15m
=45m
iv).The time taken to stop once the driver has started to brake.
t= v
a
t= 15 m/ s
7.5 ms−2
t=2s
b). In the space below, sketch a velocity-time graph to represent this event.
The following are the data obtained
Time(s) Velocity(m/s)
0 15
2 15
4 0
The graph is given as:
Velocity (m/s)
0 0.5 1 1.5 2 2.5 3 3.5 4 4.5
0
2
4
6
8
10
12
14
16
Time(s)
References
1. Crew, Henry (2008). The Principles of Mechanics. BiblioBazaar, LLC. p. 43.
2. Lehrman, Robert L. (1998). Physics the Easy Way. Barron's Educational Series.
3. Raymond A. Serway; Chris Vuille; Jerry S. Faughn (2008). College Physics, Volume
10.
4. Larry C. Andrews; Ronald L. Phillips (2003). Mathematical Techniques for Engineers
and Scientists.
5. David C. Cassidy; Gerald James Holton; F. James Rutherford (2002). Understanding
physics. Birkhauser.
6. Robert Resnick and Jearl Walker, Fundamentals of Physics, Wiley; 7 Sub edition (June
16, 2004).
7. David C. Cassidy; Gerald James Holton; F. James Rutherford (2002). Understanding
physics. Birkhauser.
8. Keith Johnson (2001). Physics for you: revised national curriculum edition for
GCSE (4th ed.). Nelson Thornes.
0
2
4
6
8
10
12
14
16
Time(s)
References
1. Crew, Henry (2008). The Principles of Mechanics. BiblioBazaar, LLC. p. 43.
2. Lehrman, Robert L. (1998). Physics the Easy Way. Barron's Educational Series.
3. Raymond A. Serway; Chris Vuille; Jerry S. Faughn (2008). College Physics, Volume
10.
4. Larry C. Andrews; Ronald L. Phillips (2003). Mathematical Techniques for Engineers
and Scientists.
5. David C. Cassidy; Gerald James Holton; F. James Rutherford (2002). Understanding
physics. Birkhauser.
6. Robert Resnick and Jearl Walker, Fundamentals of Physics, Wiley; 7 Sub edition (June
16, 2004).
7. David C. Cassidy; Gerald James Holton; F. James Rutherford (2002). Understanding
physics. Birkhauser.
8. Keith Johnson (2001). Physics for you: revised national curriculum edition for
GCSE (4th ed.). Nelson Thornes.

1 out of 13
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
© 2024 | Zucol Services PVT LTD | All rights reserved.

