Pipe Network System | Assignment

Table of Contents
Notes on the exercise.................................................................................................................................2
Appendices.................................................................................................................................................5
Appendix 1: piping_network.m code................................................................................................5
Appendix 2: run_piping.m code........................................................................................................7
References..................................................................................................................................................8
List of Figures
Figure 1 : Validation file results....................................................................................................................3
Figure 2 : Test results from actual data..........................................................................................................3

1
Notes on the exercise
This exercise involves solving a pipe network system. We are concerned with the
flow rates at various nodes and the average velocity of the flow. These parameters are
governed by the given set of equations and constraints. The parameters and
constraints are given in matrix and vector forms. This makes it appropriate to solve
using linear algebra.
The task is recurrent since it might be desired to solve various systems at any given
time. However, all the system are of the same form, in that the following parameters
are given:
1. Flow rate matrix N which represents the nodes and constraints of the system
2. Vector C which represents flow and geometric properties for each edge
3. Matrix Q which represents the equilibrium flow conditions
4. Two pressure values: one at the inlet and another at the outlet of the system
Given the scenario, it is appropriate to develop a CAD solution which can be used to
solve recurrent problems of such kind, based on the parameters given.
MATLAB software is used to develop a solution. To make it reusable and easy for
testing, a function is used instead of a flat (procedural) MATLAB file. The function is
developed in a dedicated .m file which bears the same name with the function. This
means that the function can only be called from external file and running the unction
directly from MATLAB ‘run’ button will result to an error (Folkmar Bornemann,
2018). This choice was informed by the need to validate that the function actually
works as expected, from the validation file given by the course instructor. In coputer
programming, validation is a process of evaluating software program so as to ensure
that the software meets the pre-defined and specified requirements as well as the end
users’ expectations (Kanti Bhushan Datta, 2017). The validation calls the function by
name and the convention to have this working is to have the function in a file which
bears the same name as the function itself.
The results of the validation function as shown in Figure 1(MATLAB screen shot)

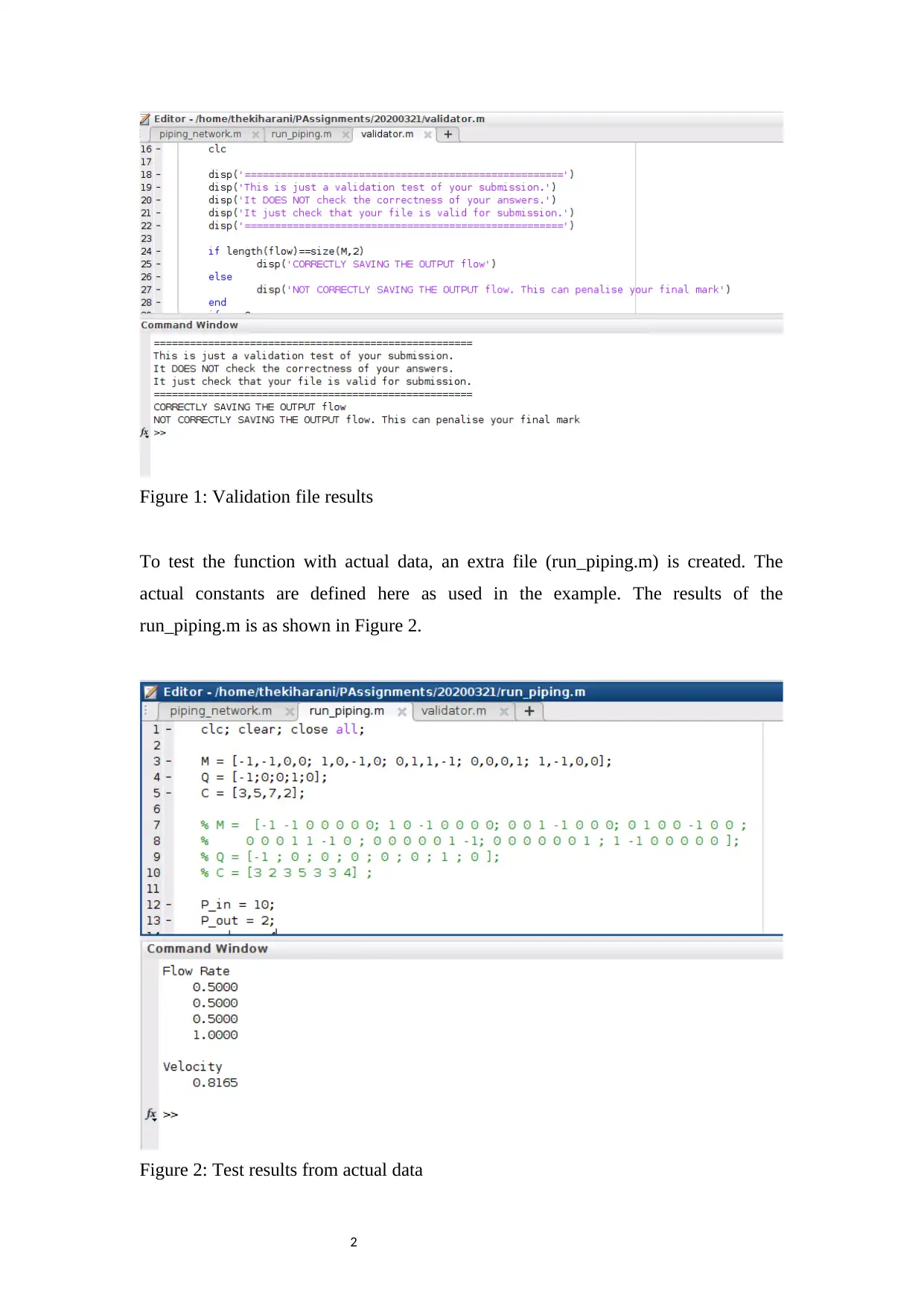
2
Figure 1: Validation file results
To test the function with actual data, an extra file (run_piping.m) is created. The
actual constants are defined here as used in the example. The results of the
run_piping.m is as shown in Figure 2.
Figure 2: Test results from actual data

3
The MATLAB files are well annotated with comments. This is preferred since the it
makes it easier for the reader to read through the code as compared to giving the
explanation in a word document. The two files (piping_network.m and run_piping.m)
are attached in the appendices.

4
Appendices
Appendix 1: piping_network.m code
% % DEFINE THE FUNCT
%{
Note: In MATLAB, the function is defines after the logic using the function
if it
has to be defined in the same m-file
%}
function[flow, v] = piping_network(nnodes, M, Q, C, P_in, P_out)
% % VALIDATING THE INPUT PARAMETERS
% define default values of flow and v
d_flow = zeros(size(M,2),1);
d_v = 0;
% verify nnodes is a positive number
if nnodes < 0
uiwait(msgbox('Error! The nnodes value must be zero or a positive
integer.'));
flow = d_flow;
v = d_v;
return;
end
% verify the length of Q == rows in M
if length(Q) ~= size(M,1)
uiwait(msgbox('Error! The length of Q must be equal to the rows in
M.'));
flow = d_flow;
v = d_v;
return;
end
% verify all elements in C are positive
if ~all(C >= 0)
uiwait(msgbox('Error! All elements in C must be posivite.'));
flow = d_flow;
v = d_v;
return;
end
% verify the length of C == columns in M
if length(C) ~= size(M,2)
uiwait(msgbox('Error! The length of C must be equal to the columns in
M.'));
flow = d_flow;
v = d_v;
return;

5
end
% verify that P_out =< P_in
if P_out > P_in
uiwait(msgbox('Error! The pressure at the inlet must be higher that at
the outlet.'));
flow = d_flow;
v = d_v;
return;
end
% % COMPUTING THE FLOW MATRIX
% calculate P as: P = -P_in + P_out
P = -P_in + P_out;
% extract the matrix of linear indpendent rows from M and assign to A
% mathch the dimentions of Q to multiply; assign to B to be nultiplied by A
% initialise variable I with indexes of linearly independent rows of M
[~,I] = rref(M');
% initialise variable A with only rows of index I of M
A = M(I, :);
% initialise variable B with only rows of index I of Q
B = Q(I, :);
% find flow values by solving the linear system
flow = linsolve(A,B);
% % SOLVING FOR VELOCITY
% find path (D) connecting first and last node and sum corresponding
constant values
D = 0;
id_node = 1;
k = size(M,2);
while id_node < nnodes
for j = 1:size(M,2)
elem = M(id_node, j);
if elem == -1
D = D + C(j);
id_node = id_node + 1;
break;
end
end
end
% velocity equation: (Dv^2 + P = 0, where P = (-P_in + P_out))
V2 = [D 0 P];
% solve for average velocity and take only the positive value
V = roots(V2);
v = V(V > 0);

6
end
Appendix 2: run_piping.m code
clc; clear; close all;
M = [-1,-1,0,0; 1,0,-1,0; 0,1,1,-1; 0,0,0,1; 1,-1,0,0];
Q = [-1;0;0;1;0];
C = [3,5,7,2];
% M = [-1 -1 0 0 0 0 0; 1 0 -1 0 0 0 0; 0 0 1 -1 0 0 0; 0 1 0 0 -1 0 0 ;
% 0 0 0 1 1 -1 0 ; 0 0 0 0 0 1 -1; 0 0 0 0 0 0 1 ; 1 -1 0 0 0 0 0 ];
% Q = [-1 ; 0 ; 0 ; 0 ; 0 ; 0 ; 1 ; 0 ];
% C = [3 2 3 5 3 3 4] ;
P_in = 10;
P_out = 2;
nnodes = 4;
[flow, v] = piping_network(nnodes, M, Q, C, P_in, P_out);
disp('Flow Rate')
disp(flow);
disp('Velocity')
disp(v);

7
References
Folkmar Bornemann. (2018). Numerical linear algebra : a concise introduction with
MATLAB and Julia. New York: Springer.
Kanti Bhushan Datta. (2017). Matrix And linear algebra aided with MATLAB. Delhi
Phi Learning Private Limited.