Power System Analysis Part 2 .

This article discusses HVDC transmissions, line parameters, compensation, ABCD parameters, surge impedance loading, and more in Power System Analysis Part 2. It also includes calculations for interrupting capacity, pu impedance, fault MVA, and fault current. Subject: Power System Analysis, Course Code: N/A, Course Name: N/A, College/University: N/A

ASSIGNMENT: Power system Analysis Part 2

ASSIGNMENT: Power system Analysis Part 2
Ans:
HVDC transmissions can be used for over long distance.In transmission line there is many parameters
are Important to calculate which voltage (KV) line we should use in transmission. Such Parameters are
distance (in km),line voltage (KV), resistance (ohm),series inductance, shunt capacitance, surge
impedance loading , Input and output power, active and reactive power, transmission parameters
(ABCD),efficiency, susceptance and compensators.
From given data overhead line is 280 km away from hydroelectric stations.
So,
Distance between lines: 280 Km
Full load: 1500 MW
Power factor cos (φ)=0.95 (lagging)
Φ=18.1949o
Line representation=π equivalent circuit with half the capacitance at either end.
Line compensation=40%
Synchronous compensation=300 MVAr
Maximum permissible voltage drop =10%
Transmission angle=30 o
From the table-1 we observed that , when overhead line voltages has increases from 132 Kv,275 Kv and
400 Kv, than the resistance is decreases, reactance is increases, susceptance is increases and surge
impedance is decreases.
All the parameters are in per phase per km.
Consider nominal π method:

ASSIGNMENT: Power system Analysis Part 2
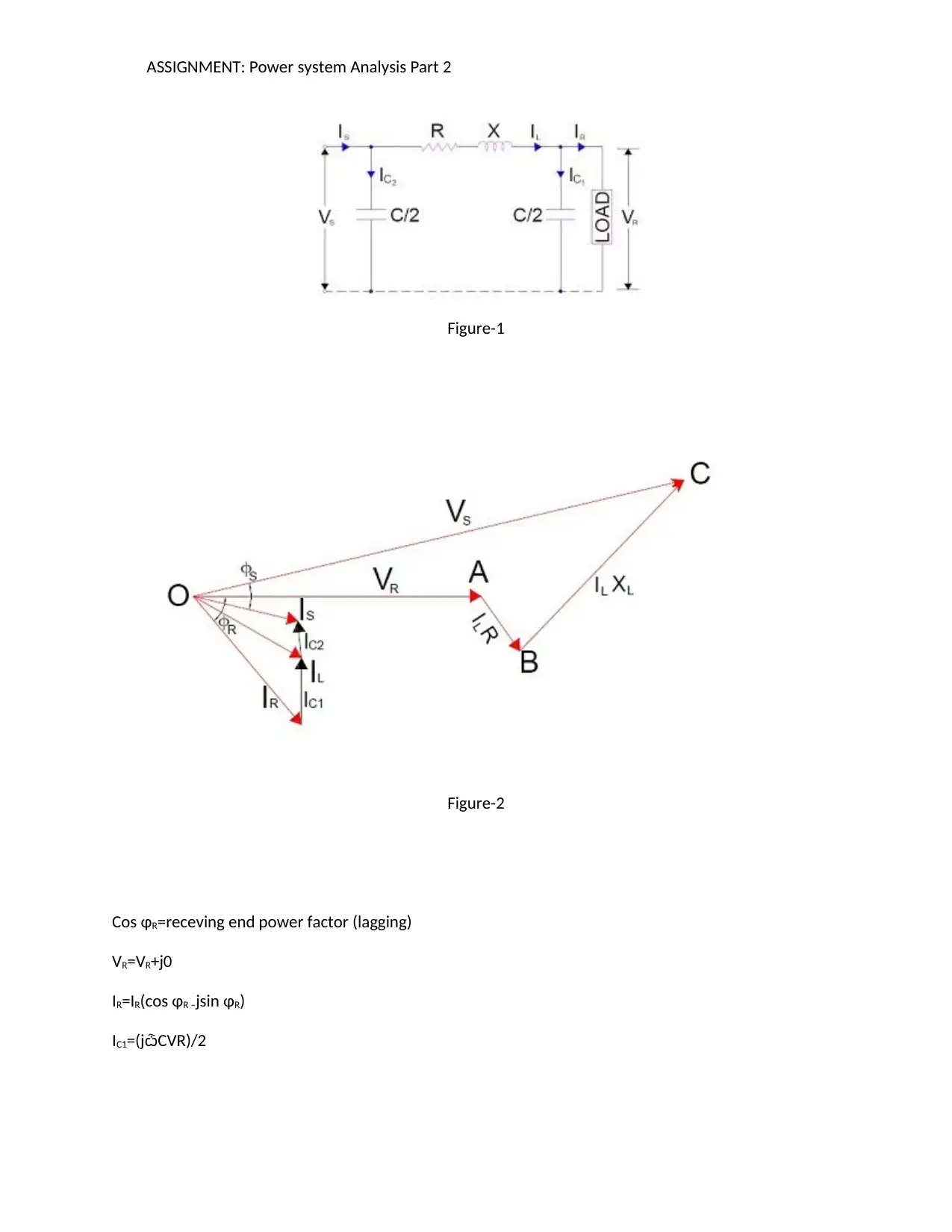
Figure-1
Figure-2
Cos φR=receving end power factor (lagging)
VR=VR+j0
IR=IR(cos φR –jsin φR)
IC1=(jѽCVR)/2

ASSIGNMENT: Power system Analysis Part 2
IL=IR+IC1
VS=VR+IL(R+jX)
IC2= (jѽCVs)/2
Is=IL+IC2
Relation between distance and voltage in transmission line(V)=5.5 √0.62 L+(3 P/150)
From the table-1
L=280 Km
Line voltage= 5.5 √0.62∗( 280 )+ ( 3∗1500000
150 )
=955 KV
So at 280 Km distance line voltage of overhead line can be 400 KV
Series compensation:
It improve system voltage. In this reactive power is inserted in series with the line for improving the
impedance of the system. It also improve power transfer capacity and stability.
If XC is connected in series with the line than the reactance of the line is reduces from XL to (XL-XC). The
power transfer to receiving end is given by:
P2= Vs VR sinα/(XL-XC) where α is angle between VR and VS
P2/P1= XL/( XL-XC)
=1/(1-(XC/XL))
= 1/(1-K)
Here k is degree of compensation
K=( XC/XL)*100
XL= total series inductive reactance

ASSIGNMENT: Power system Analysis Part 2
Xc= capacitive reactance of the capacitor bank
K should be lie between 0.4 to 0.7
If K =0.5
Than P2/P1= 2
It means power transfer is double by 50 % compensation
If K=0.4
Than P2/P1= 1.67
It means power transfer is 1.67 time by 40 % compensation
Improving system stability: In compensated lines α is less. If we decreases the value of α than its
gives high stability.
Synchronous compensator: it is used to improve power factor and regulate the voltage in power lines.
If the load is high and inductive synchronous compensator is operating in the over excited mode than it
is equivalent to the capacitive load.
Active Power (P)= MW
Reactive power in inductor (Q)= MVAr
Reactive power in capacitor (Q)= MVAr
Distance of the overhead line:
As we know 1 mile= 1.60934 Km
For HVDC transmission, due to the large cost , it is necessary to convert signals from AC to Dc and back
DC to AC for long distance (greater than 400 mile = 643.738 Km) overhead power lines.
Consider given following figure of transmission lines.

ASSIGNMENT: Power system Analysis Part 2
Figure-3
Rdc= pl/A
DC resistance is proportional to the temperature. Rdc is increases with increases in temperature over the
normal range of temperature.
pT2= (M+T2)/(M+T1)*pT1
Wire manufacture usually supply cables of resistance per unit length at common frequency.
Rdc(ohm/1000ft) at 20 = 0.0644,0.0637,0.510……so on
Series Inductance:
It is defined as the number of flux leakage produced per ampere of current flowing through the lines.
Inductance of single phase transmission:
L=ƛ/I
Phase of the high voltage overhead line must be spaced further apart to ensure proper insulation. At
high voltage line will have a higher inductance than a low voltage lines.
So high voltage =high inductance
High resistance = low inductance and reduce corona losses also.

ASSIGNMENT: Power system Analysis Part 2
From Formula
GMR2=(GMRd)1/2
Shunt Capacitance:
C=q/V here q= charge V =applied voltage
€=8.85 * 10-12 F/m
Capacitance= 2π€/ln(D/r)
High Space between lines = low capacitance
High voltage = low capacitance
High Resistance = High capacitance
Bundling also increases the capacitance
Inductive Reactance:
XL= 0.1213 ln(GMD/GMR)
ABCD parameter in transmission line:
In short lines shunt admittance is not included but in medium and long distance lines it is included.
Transmission parameters are depend on ABCD parameters. Convert π network in 2 port network.

ASSIGNMENT: Power system Analysis Part 2
Figure-4
Vs= A VR + B IR
Is= C VR + D IR
From calculations A= ZY/2+1
B= Z
C= Y(ZY/4+1)
D= ZY/2+1
Surge Impedance Loading:
It is defined as power delivered by a line to a pure resistive load that is equal to its surge impedance.
It is defined as Zc= (L/C)1/2
SIL= VL2/(L/C)1/2 Mw

ASSIGNMENT: Power system Analysis Part 2
Under such loading the line consume as much reactive power as it generate and terminal voltage are
equal to each other’s.
In transmission line both absorbs and generates reactive power.
1) Under light load, the line generate more reactive power than its consume.
2) Under surge impedance loading the line generates and consumed the same amount of reactive
power.
Under heavy load, the line absorb more reactive power than it’s generate.
Input and Output efficiency:
Input power= Pin= √3 VsIscos θs
Qin=√ 3 VsIs sin θs
Sin= √3 VsIs
Output Power
Pin= √3 VrIr cos θr
Qin=√ 3 VrIr sin θr
Sin= √3 VrIr
Efficiency= (Pout/pin) * 100
Long line series and shunt compensation:
Shunt reactors are used to compensate the line shunt capacitance under light load of no load to regulate
voltage.

ASSIGNMENT: Power system Analysis Part 2
Series capacitors:
It is used to compensate the line inductive reactance in order to transfer more power.
Susceptance:
It is in form of energy is alternately stored in and released from a magnetic field or an electric field.
In magnetic field the susceptance is inductive. In electric field it is capacitive.
In inductive susceptance is assigned negative imaginary number and capacitive susceptance it is
assigned as positive imaginary number.
When
Inductance increases= S increases (smaller negatively)
Capacitance increases= S increases (larger positively)
Conclusion:
We conclude that we can use 400 KV line for 280 km transmission line at 1500 MWatt full load at 0.95
power factor. In this it decreases resistance so that energy loss in the form of heat decreases. Reactance
is also decreases so more power can be transmitted and also improve stability of transmission line.
Efficiency is also better than short transmission line.

ASSIGNMENT: Power system Analysis Part 2

ASSIGNMENT: Power system Analysis Part 2
NB: The submission deadline for this assignment is 1/1/2019 at 12:00pm and the submission will only be
accepted through webcourses. Penalties for late submission will be applied as per the programme
document.

ASSIGNMENT: Power system Analysis Part 2
Given Data:
VG1=20 KV
Apparent Power of G1=100 MVA
X’G1=0.12 pu
VG2=20 KV
Apparent Power of G2=100 MVA
X’G2=0.12 pu
Apparent Power of T1=100 MVA
X’T1=0.1 pu
Apparent Power of T2=100 MVA
X’T2=0.1 pu
Feeder Length L=40 Km
Z=(0.035+j0.14) ohm/km
VG2=20 KV
VT3=11 KV
Apparent Power of T3=100 MVA
X’T3=0.1 pu
Common Base: 100 MVA

ASSIGNMENT: Power system Analysis Part 2
Interrupting Capacity in a circuit breaker is the maximum current which is rated to safely interrupt at a
specific voltage. This short circuit current rating is normally express in rms symmetrical amperes and is
specified by current magnitude only.
It is also defend as the maximum fault current that can be interrupt by a circuit breaker without failure
of the circuit breaker.
Interrupting capacity= [ √3∗Rated line voltage ( Vrms )∗Rated Line Current ( Arms ) ]∗10−6
Rated line current= V/Z
(11)/¿)
=11/(40*0.144308696)
=1.90 A
=√3∗
( 11000
√2 )∗
(1.90
√2 )∗10−6
=18.099 *10-3 MVA
=0.0180 MVA
Rated symmetrical breaking current=
=Interrupting capacity/( √3∗rated voltage)
= (18.099* 10-3)/(√3∗(11/ √ 2))
=1.3434 A
Making capacity= 2.55* Rated symmetrical breaking current
=3.4256 A

ASSIGNMENT: Power system Analysis Part 2
Pu impedance=base MVA/fault MVA
Fault MVA=Base MVA/ Equivalent Impedance
pu reactance=(% Reactance /100)*(base MVA/Actual MVA)
pu reactance of G1= (0.12)*(100/100)
=0.12
pu Impedance of G2= (0.12)*(100/100)
=0.12
pu Impedance of T1= (0.1)*(100/100)
=0.1
pu Impedance of T2= (0.1)*(100/100)
0.1
pu Impedance of T3=(0.12)*(100/100)
=0.12
Equivalent impedance={[( 0.12+0.1) * (0.12+0.1)]/[ ( 0.12+0.1) +(0.12+0.1)]]}+0.12
=0.11+0.12
=0.23
Xeq=0.23
Fault MVA= 100 MVA/0.23
=434.7827 MVA
Fault Current={(434.7827)/( √ 3∗ ( 11 )∗1000)}*106
=22.820 KA

ASSIGNMENT: Power system Analysis Part 2