Building and Evaluating Predictive Models for Desklib

This article discusses data exploration and cleaning techniques and building predictive models using real world business case with Desklib. It covers continuous and categorical variables, summary statistics, missing values, and correlation analysis.

Building and Evaluating Predictive Models
Part A: DATA EXPLORATION AND CLEANING
The first part of the research is focused on the data exploration and the cleaning of the given
data. For this part the cereals (for breakfast) data has been used. This data set contains 76 data
points and 18 different features. The results from the data exploration
1. The list of the continuous variables are shown in the table below.
## [1] "Calories" "Protein" "Fat"
## [4] "Sodium" "Fiber" "Complex.Carbos"
## [7] "Tot.Carbo" "Sugars" "Calories.fr.Fat"
## [10] "Potassium" "Enriched" "Wt.serving"
## [13] "cups.serv"
pTable 1 list of the numerical variables
Categorical variables are shown in the table below. The categorical variables are those variables
where there are more than one category. There are two types of the categorical variables. The
first one is the nominal variable where there is no particular order of the category. Secondly, the
other type of categorical variable is the ordinal variable, where the category have particular
order. In the current case among all the categorical variables, only Fibre.gr is the ordinal
variable. All other variables are the nominal variable.
# Ordinal: Fiber.Gr
# Nominal: Name, Manufacturer, Mfr, Hot.Cold
Table 2 Ordinal and the nominal variables

2. The summary statistics for the continuous variables has been calculated and for the
calculation purpose various measures of the central tendencies such as mean and median
has been included. The results are shown in the table below.
Calories Protein Fat Sodium
## C:73 Min. : 50.0 Min. :1.00 Min. :0.000 Min. : 0.0
## H: 3 1st Qu.:110.0 1st Qu.:2.00 1st Qu.:0.500 1st Qu.:147.5
## Median :120.0 Median :3.00 Median :1.000 Median :210.0
## Mean :140.5 Mean :3.25 Mean :1.447 Mean :194.9
## 3rd Qu.:192.5 3rd Qu.:5.00 3rd Qu.:2.000 3rd Qu.:262.5
## Max. :250.0 Max. :7.00 Max. :9.000 Max. :420.0
##
Fiber Complex.Carbos Tot.Carbo Sugars
## Min. : 0.000 Min. : 7.00 Min. :11.00 Min. : 0.000
## 1st Qu.: 1.000 1st Qu.:13.00 1st Qu.:24.00 1st Qu.: 4.000
## Median : 3.000 Median :17.50 Median :27.00 Median :11.000
## Mean : 3.066 Mean :19.16 Mean :31.37 Mean : 9.145
## 3rd Qu.: 5.000 3rd Qu.:26.00 3rd Qu.:41.00 3rd Qu.:14.000
## Max. :13.000 Max. :38.00 Max. :50.00 Max. :20.000
Calories.fr.Fat Potassium Enriched Wt.serving
## Min. : 0.00 Min. : 0.0 Min. : 0.00 Min. :12.00
## 1st Qu.: 5.00 1st Qu.: 35.0 1st Qu.: 25.00 1st Qu.:30.00
## Median :10.00 Median : 92.5 Median : 25.00 Median :30.00

## Mean :12.37 Mean :122.0 Mean : 28.62 Mean :36.65
## 3rd Qu.:20.00 3rd Qu.:200.0 3rd Qu.: 25.00 3rd Qu.:49.00
## Max. :50.00 Max. :390.0 Max. :100.00 Max. :60.00
## NA's :13
cups.serv Fiber.Gr
## Min. :0.3300 Low :33
## 1st Qu.:0.7500 Medium:32
## Median :1.0000 High :11
## Mean :0.8911
## 3rd Qu.:1.0000
## Max. :1.3300
Table 3 Table for the summary statistics
The summary statistics of the continuous variable is shown in the table above. On the basis of the
results, the variable which has extreme values is the potassium. In case of potassium the mean value is
194 whereas the minimum and the maxim value are 0 and 420 respectively. Similarly the range of
calories also lies between as low as 50 to as high as 250.
Count of the categorical variables
100% Bran : 1 American Home: 1 A: 1
## 100% Nat. Bran Oats & Honey : 1 General Mills:25 G:25
## 100% Nat. Low Fat Granola w raisins: 1 Kelloggs :23 K:23
## All-Bran : 1 Nabisco : 5 N: 5
## All-Bran with Extra Fiber : 1 Post :10 P:10
## Almond Crunch w Raisins : 1 Quaker Oats :12 Q:12
## (Other) :70

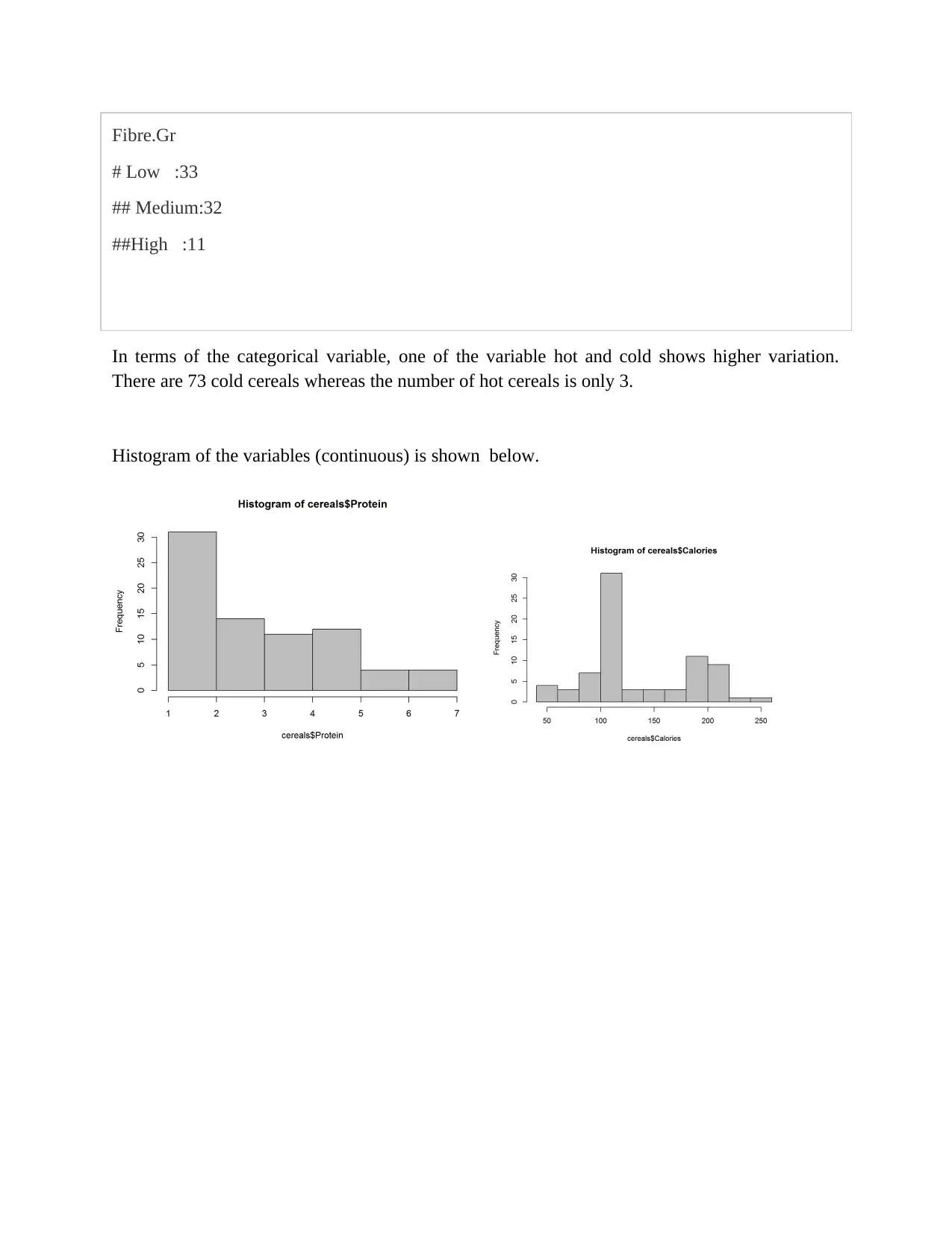
Fibre.Gr
# Low :33
## Medium:32
##High :11
In terms of the categorical variable, one of the variable hot and cold shows higher variation.
There are 73 cold cereals whereas the number of hot cereals is only 3.
Histogram of the variables (continuous) is shown below.

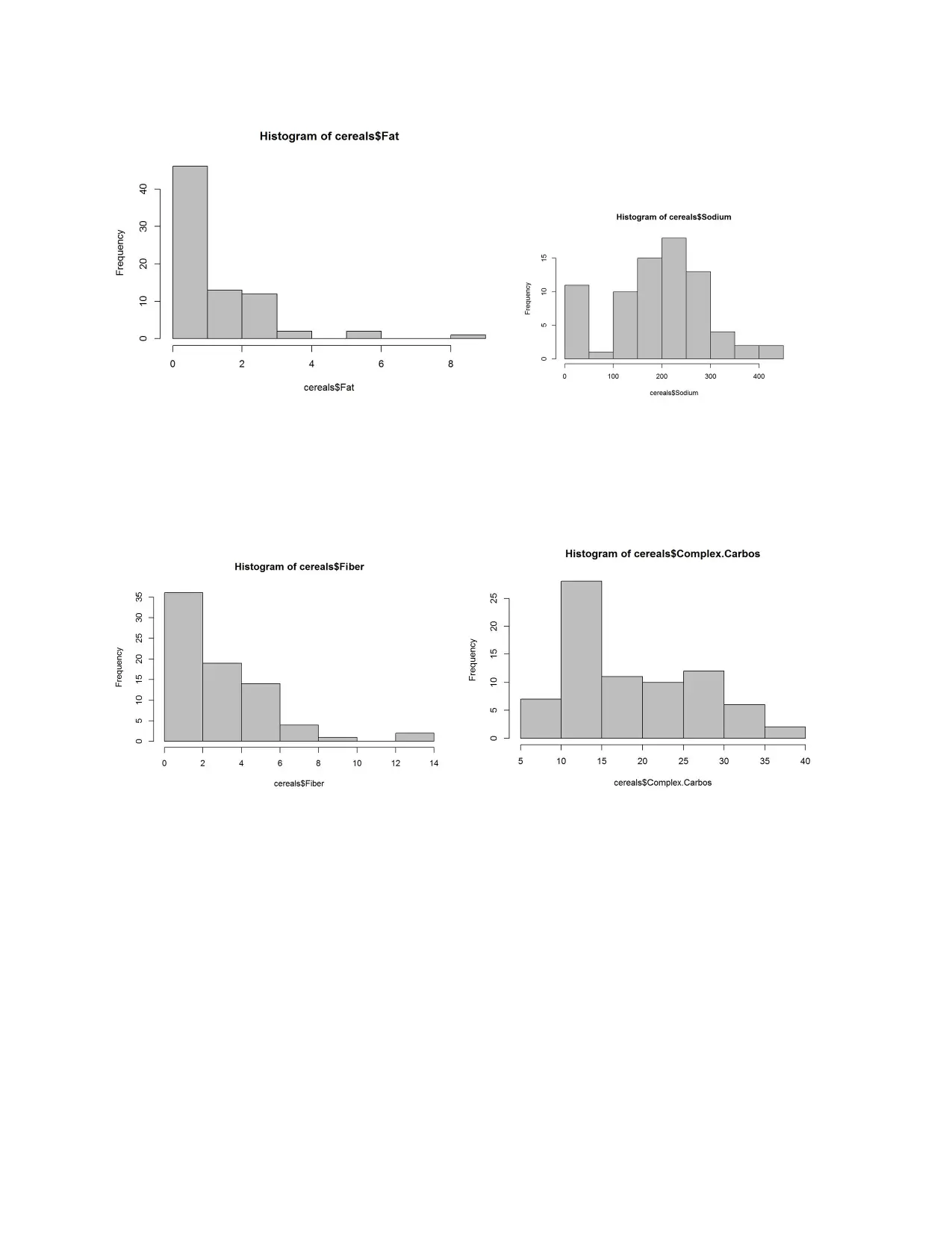
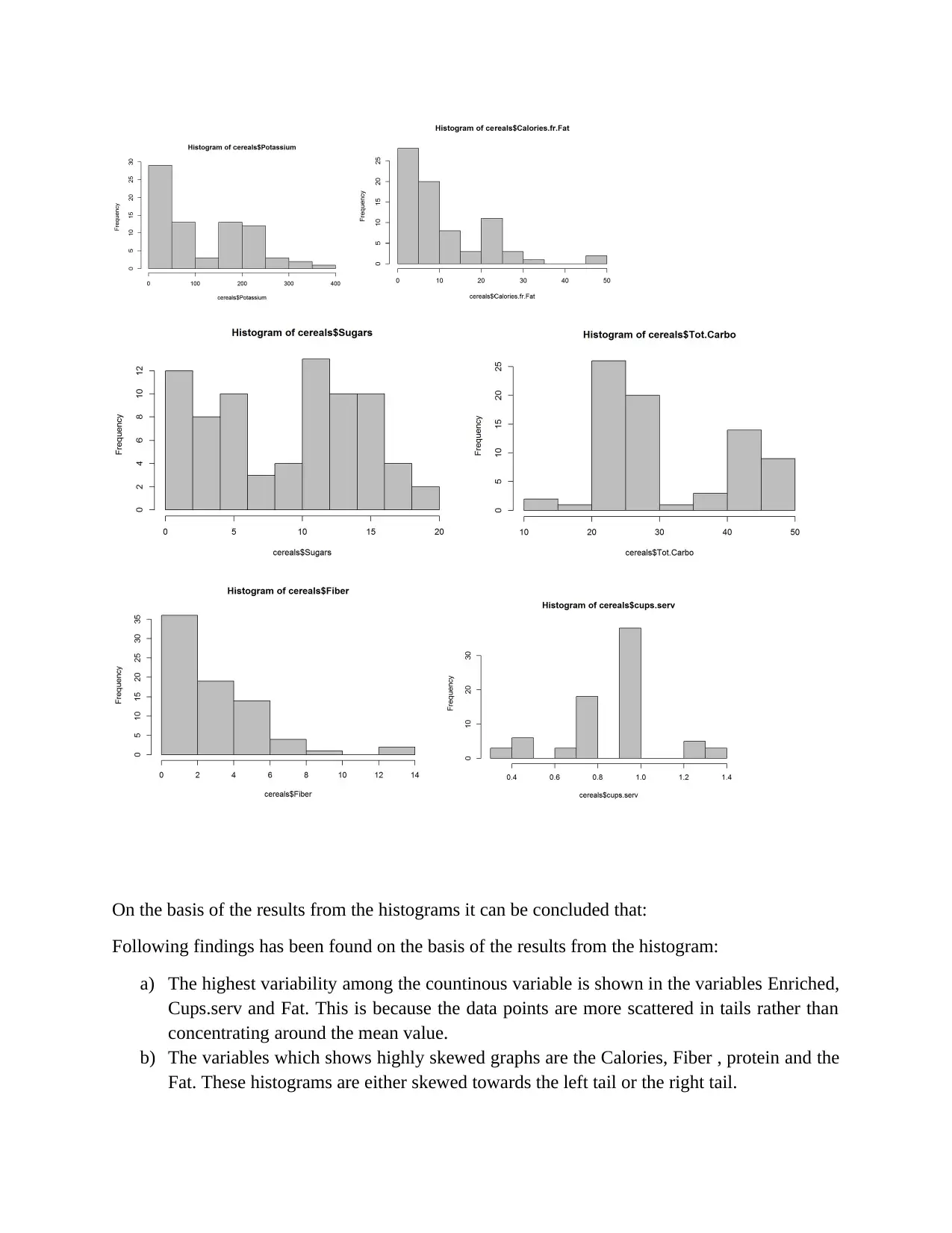
On the basis of the results from the histograms it can be concluded that:
Following findings has been found on the basis of the results from the histogram:
a) The highest variability among the countinous variable is shown in the variables Enriched,
Cups.serv and Fat. This is because the data points are more scattered in tails rather than
concentrating around the mean value.
b) The variables which shows highly skewed graphs are the Calories, Fiber , protein and the
Fat. These histograms are either skewed towards the left tail or the right tail.

c) In terms of the extreme values, Calories.fr.fate and Enriched are the variables with some
outliers.
4) Missing values
varlist nmiss complete complete_per mean median minimum
## 1 Calories 0 76 100.00000 140.5263158 120.0 50.00
## 2 Protein 0 76 100.00000 3.2500000 3.0 1.00
## 3 Fat 0 76 100.00000 1.4473684 1.0 0.00
## 4 Sodium 0 76 100.00000 194.8684211 210.0 0.00
## 5 Fiber 0 76 100.00000 3.0657895 3.0 0.00
## 6 Complex.Carbos 0 76 100.00000 19.1578947 17.5 7.00
## 7 Tot.Carbo 0 76 100.00000 31.3684211 27.0 11.00
## 8 Sugars 0 76 100.00000 9.1447368 11.0 0.00
## 9 Calories.fr.Fat 0 76 100.00000 12.3684211 10.0 0.00
## 10 Potassium 0 76 100.00000 121.9736842 92.5 0.00
## 11 Enriched 0 76 100.00000 28.6184211 25.0 0.00
## 12 Wt.serving 13 63 82.89474 36.6507937 30.0 12.00
## 13 cups.serv 0 76 100.00000 0.8910526 1.0 0.33
In the current case only Wt. serving has missing values where 13 data points are missing. To
handle the missing data 3 different methods has been used namely the mean value imputation,
median value imputation and the mode value imputation. In mean value imputation the missing
values are replaced by the mean value of the series. Similarly in the median and the mode value
imputation the median and the mode values are replaced in place of the missing values.
varlist nmiss complete complete_per mean median minimum
Wt.serving 13 63 82.89474 36.6507937 30.0 12.00

The transformation of the mean value imputation in the wt.serving is shown in the figure above.
This shows that with the mean value imputation, now more values lies around the mean.
However there are still some extreme values in the data set.

Part B : Building predictive models using real world business case
After the data exploration in the first section, the second section deals with the model building.
In this case using the car sales data of Toyota Corolla, the prediction model has been developed.
The data set contains the data for 37 different features for 1400 cars sold Australia.
1) Data Exploration and Cleaning
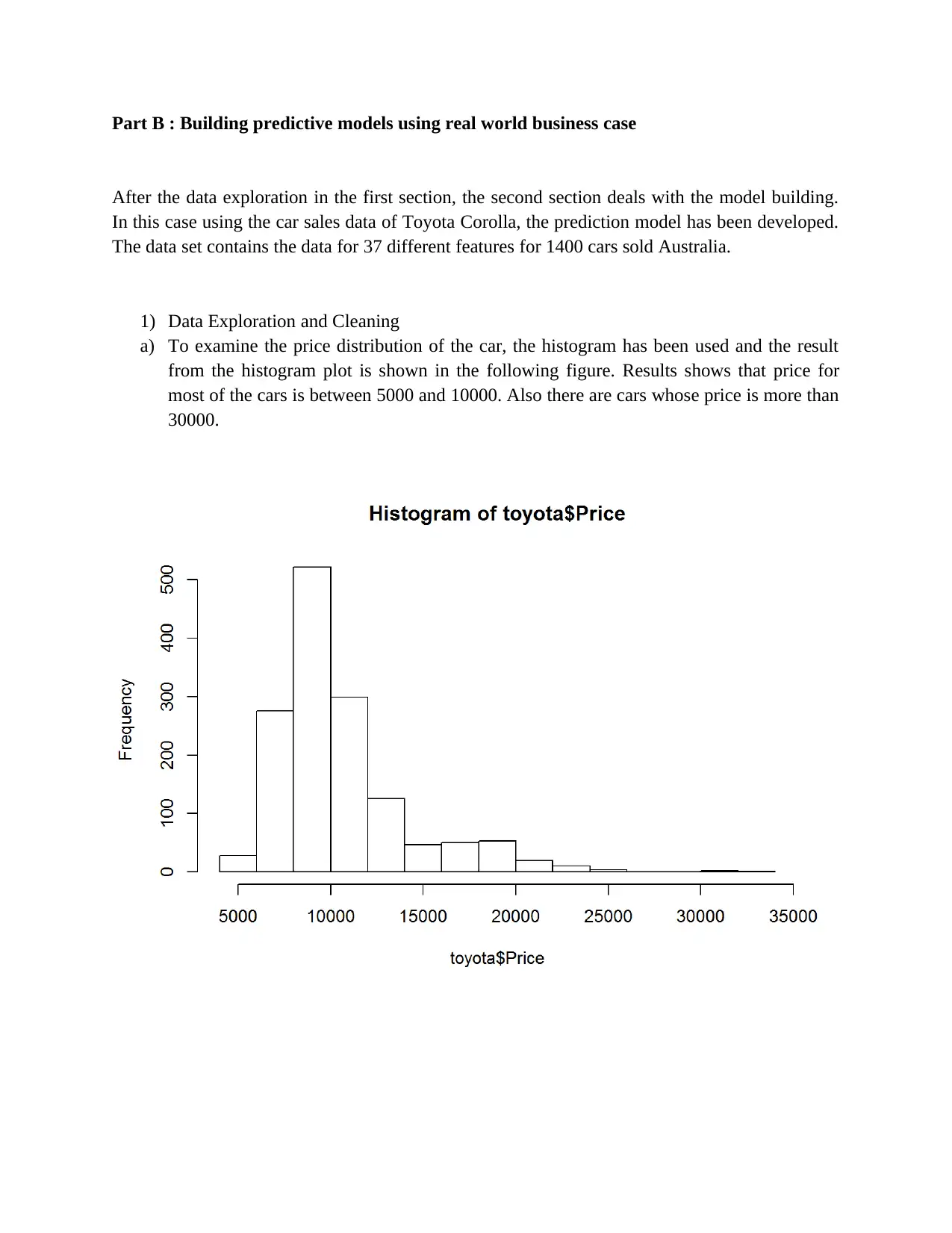
a) To examine the price distribution of the car, the histogram has been used and the result
from the histogram plot is shown in the following figure. Results shows that price for
most of the cars is between 5000 and 10000. Also there are cars whose price is more than
30000.

Min. 1st Qu. Median Mean 3rd Qu. Max.
4350 8450 9900 10731 11950 32500
Furthermore the results from the descriptive statistics indicates that the average price of the
Toyota Corolla car is 10731. As discussed the price range from as low as 4350 to as high as
32500. This also indicates that there are some outliers in the data set.
b) Checking for the missing values
Results from the analysis indicates there is no case of missing values in the current data set.
varlist nmiss complete complete_per
## 1 Id 0 1436 100
## 2 Model 0 1436 100
## 3 Price 0 1436 100
## 4 Age_08_04 0 1436 100
## 5 Mfg_Month 0 1436 100
## 6 Mfg_Year 0 1436 100
## 7 KM 0 1436 100
## 8 Fuel_Type 0 1436 100
## 9 HP 0 1436 100
## 10 Met_Color 0 1436 100
## 11 Automatic 0 1436 100
## 12 cc 0 1436 100
## 13 Doors 0 1436 100
## 14 Cylinders 0 1436 100
## 15 Gears 0 1436 100
## 16 Quarterly_Tax 0 1436 100
## 17 Weight 0 1436 100
## 18 Mfr_Guarantee 0 1436 100
## 19 BOVAG_Guarantee 0 1436 100
## 20 Guarantee_Period 0 1436 100
## 21 ABS 0 1436 100
## 22 Airbag_1 0 1436 100
## 23 Airbag_2 0 1436 100
## 24 Airco 0 1436 100

## 25 Automatic_airco 0 1436 100
## 26 Boardcomputer 0 1436 100
## 27 CD_Player 0 1436 100
## 28 Central_Lock 0 1436 100
## 29 Powered_Windows 0 1436 100
## 30 Power_Steering 0 1436 100
## 31 Radio 0 1436 100
## 32 Mistlamps 0 1436 100
## 33 Sport_Model 0 1436 100
## 34 Backseat_Divider 0 1436 100
## 35 Metallic_Rim 0 1436 100
## 36 Radio_cassette 0 1436 100
## 37 Tow_Bar 0 1436 100
c) Since the R software is being used for the analysis, there is no need to separately convert
the categorical variables into the numerical as the software itself create dummy variables
for it.
d) Correlation Analysis
Since there are 37 variables in the data set, the correlation coefficients have been included for
only those variables which have high correlation coefficient. The correlation coefficient which
are higher than 0.8 and less than 1 has been calculated. This will eliminate the correlation
coefficients which are less. This dimension reduction has shown that manufactured year and the
age of the car are highly correlated with the price of the car. So, it is better to drop one variable.
Since the coefficient of manufacturing year is higher with price, the age has been dropped.
Furthermore among the categorical variables central lock and the power windows shows high
correlation with the price. While comparing the coefficient, it has been shown that coefficient
between price and powered windows is higher as compared to the coefficient between price and
central lock, so powered windows has been selected.
2) Regression Modelling
Regression analysis is used to predict the response variables using the explanatory variables. In
the current case, the price of the cars is the response of the dependent variable and all other
features as the explanatory variables.

The first model is as follows;
Residuals:
## Min 1Q Median 3Q Max
## -7904.0 -718.8 2.5 728.3 6027.0
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 1.058e+03 9.350e+02 1.132 0.25788
## Age_08_04 -1.169e+02 3.363e+00 -34.776 < 2e-16 ***
## Boardcomputer -2.363e+02 1.050e+02 -2.251 0.02455 *
## Automatic_airco 2.611e+03 1.658e+02 15.744 < 2e-16 ***
## Weight 1.410e+01 7.735e-01 18.227 < 2e-16 ***
## KM -1.799e-02 1.103e-03 -16.311 < 2e-16 ***
## CD_Player 2.784e+02 9.307e+01 2.991 0.00283 **
## Powered_Windows 4.329e+02 7.022e+01 6.165 9.18e-10 ***
## HP 2.086e+01 2.396e+00 8.708 < 2e-16 ***
## ABS -2.111e+02 9.186e+01 -2.298 0.02168 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1222 on 1426 degrees of freedom
## Multiple R-squared: 0.8871, Adjusted R-squared: 0.8864
## F-statistic: 1245 on 9 and 1426 DF, p-value: < 2.2e-16
In this model the R squared is 0.88 which shows that 88 % of the variation is being explained by
he explanatory variables in the model. In the next model some of the variables which were not
significant in this model were removed, such as the central lock. Similarly in the second model
the variables which were not highly significant were removed. Finally the optimal model has
been found in the third time and the results are shown in the table below. In this case all the
coefficient are highly significant and the R squared is also high. So this is considered as the
optimal model(Bai & Ng, 2009).
Coefficients:

## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 1.058e+03 9.350e+02 1.132 0.25788
## Age_08_04 -1.169e+02 3.363e+00 -34.776 < 2e-16 ***
## Boardcomputer -2.363e+02 1.050e+02 -2.251 0.02455 *
## Automatic_airco 2.611e+03 1.658e+02 15.744 < 2e-16 ***
## Weight 1.410e+01 7.735e-01 18.227 < 2e-16 ***
## KM -1.799e-02 1.103e-03 -16.311 < 2e-16 ***
## CD_Player 2.784e+02 9.307e+01 2.991 0.00283 **
## Powered_Windows 4.329e+02 7.022e+01 6.165 9.18e-10 ***
## HP 2.086e+01 2.396e+00 8.708 < 2e-16 ***
## ABS -2.111e+02 9.186e+01 -2.298 0.02168 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1222 on 1426 degrees of freedom
## Multiple R-squared: 0.8871, Adjusted R-squared: 0.8864
## F-statistic: 1245 on 9 and 1426 DF, p-value: < 2.2e-16
b) Evaluating the accuracy of the regression model
The optimal regression model can be evaluated on the basis of R squared, multicollinariy and the
statistical significance of the coefficients. In the current case the R squared is decently higher at
0.88. The Vif test indicates there is no problem of multicollinerity and the regression coefficients
are also statistically significant(Armstrong, 2012; Dufour & Dagenais, 1985; Lanfranchi, Viola,
& Nascimento, 2010).
3) Decision tree

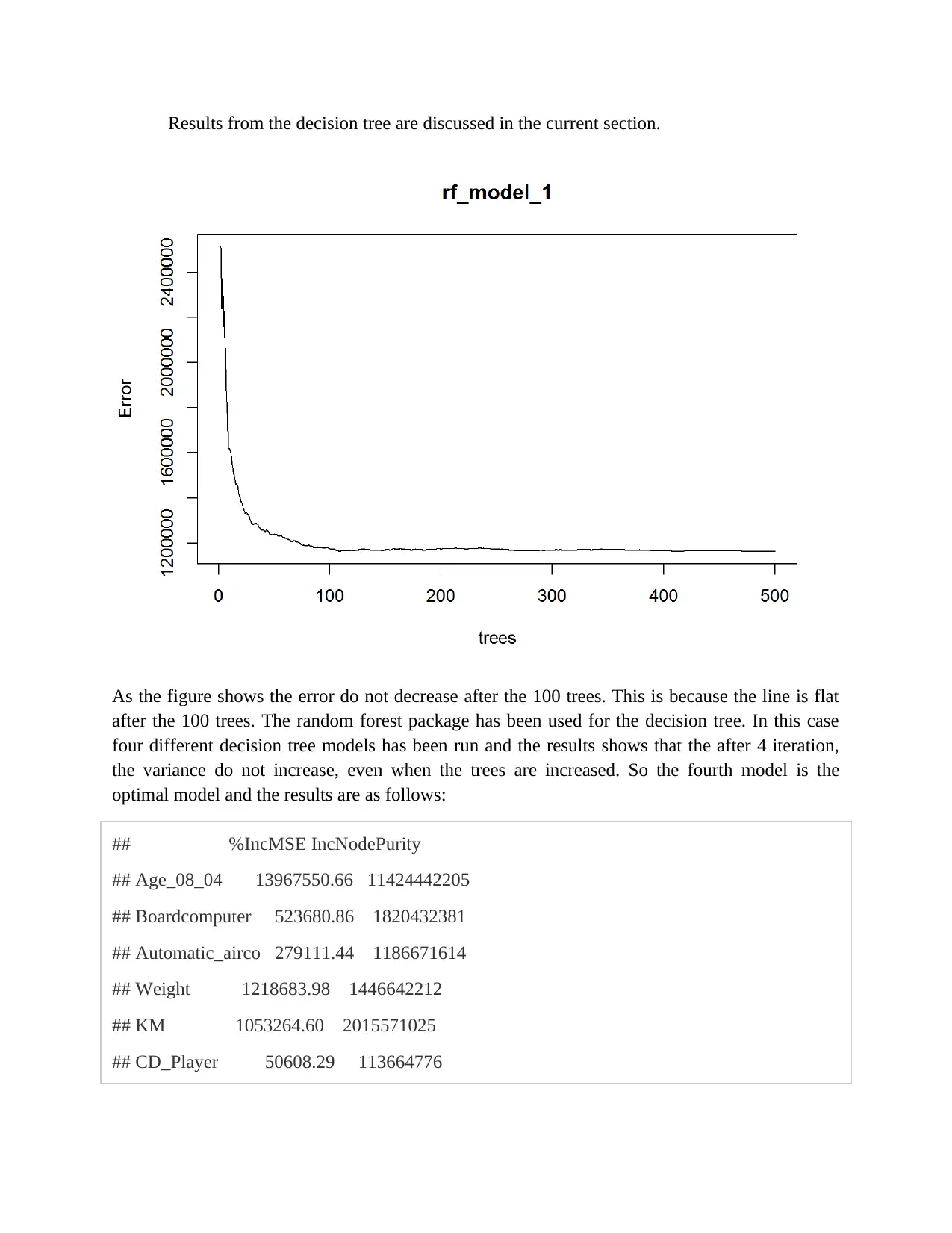
Results from the decision tree are discussed in the current section.
As the figure shows the error do not decrease after the 100 trees. This is because the line is flat
after the 100 trees. The random forest package has been used for the decision tree. In this case
four different decision tree models has been run and the results shows that the after 4 iteration,
the variance do not increase, even when the trees are increased. So the fourth model is the
optimal model and the results are as follows:
## %IncMSE IncNodePurity
## Age_08_04 13967550.66 11424442205
## Boardcomputer 523680.86 1820432381
## Automatic_airco 279111.44 1186671614
## Weight 1218683.98 1446642212
## KM 1053264.60 2015571025
## CD_Player 50608.29 113664776

## Powered_Windows 200498.28 140180060
## HP 389816.37 486749793
## ABS 11802.00 46241351
b) One of most popular method of decision tree is random forest. In some cases the decision tree
fit multiple lines in the data and predict the data. So, in some cases there is a problem of
overfittting while running the model on training data. To solve this problem the random forest
technique is used, as it builds multiple trees on the basis of the given data and give the average
prediction. This method is considered to be less biased(Fokin & Hagrot, 2016).
4) Comparison of the models
On the basis of the results from the both the regression analysis and the decision tree it can be
concluded that the decision tree is able to explain higher variance (91%) as compared to
regression ( where R squared is 0.88). However impact of each explanatory variable on the
dependent variable is missing from the random forest. So, from business point of view the
regression model is appropriate as the variables can be clearly identified.
References
Armstrong, J. S. (2012). Illusions in regression analysis. International Journal of Forecasting, 6,
689–694.
Bai, J., & Ng, S. (2009). Tests for Skewness, Kurtosis, and Normality for Time Series Data.
Journal of Business & Economic Statistics, 23(1), 49–60.
https://doi.org/10.1198/073500104000000271
Dufour, J. M., & Dagenais, M. G. (1985). Durbin-Watson tests for serial correlation in
regressions with missing observations. Journal of Econometrics, 27(3), 371–381.
https://doi.org/10.1016/0304-4076(85)90012-0
Fokin, D., & Hagrot, J. (2016). Constructing decision trees for user behavior prediction in the
online consumer market. Kth Royal Institute of technology.
Lanfranchi, L. M. M. M., Viola, G. R., & Nascimento, L. F. C. (2010). The use of Cox
regression to estimate the risk factors of neonatal death in a private NICU. Taubate.