Pricing Analytics and Revenue Management

This report analyzes the impact of price levels and other strategies on sales volume. It uses a linear regression model and log variables to explore the relationship between variables and develop new variables. The findings suggest that sales volume is not determined by the price of products but by the changes in price levels.

Pricing Analytics and
Revenue Management

Contents
INTRODUCTION...........................................................................................................................1
TASK 1............................................................................................................................................1
1. Linear regression model..........................................................................................................1
2. `Log volume' and `log price'....................................................................................................2
3 (a)..............................................................................................................................................3
3 (b)..............................................................................................................................................3
CONCLUSION................................................................................................................................4

INTRODUCTION
Price analytics is a process of analysing the prices of the goods and services which are sold
by the organisation. This concept of price analytics helps in improving profitability and market
share. The main aim of this piece of work is to analyse the sales data given in ssanner.csv. For
this purpose, in this report regression model is used to analyse the relationship between various
variables. The software application of SPSS and Microsoft Excel are used in this report to
develop new log variables and then analyse them with using linear regression model.
TASK 1
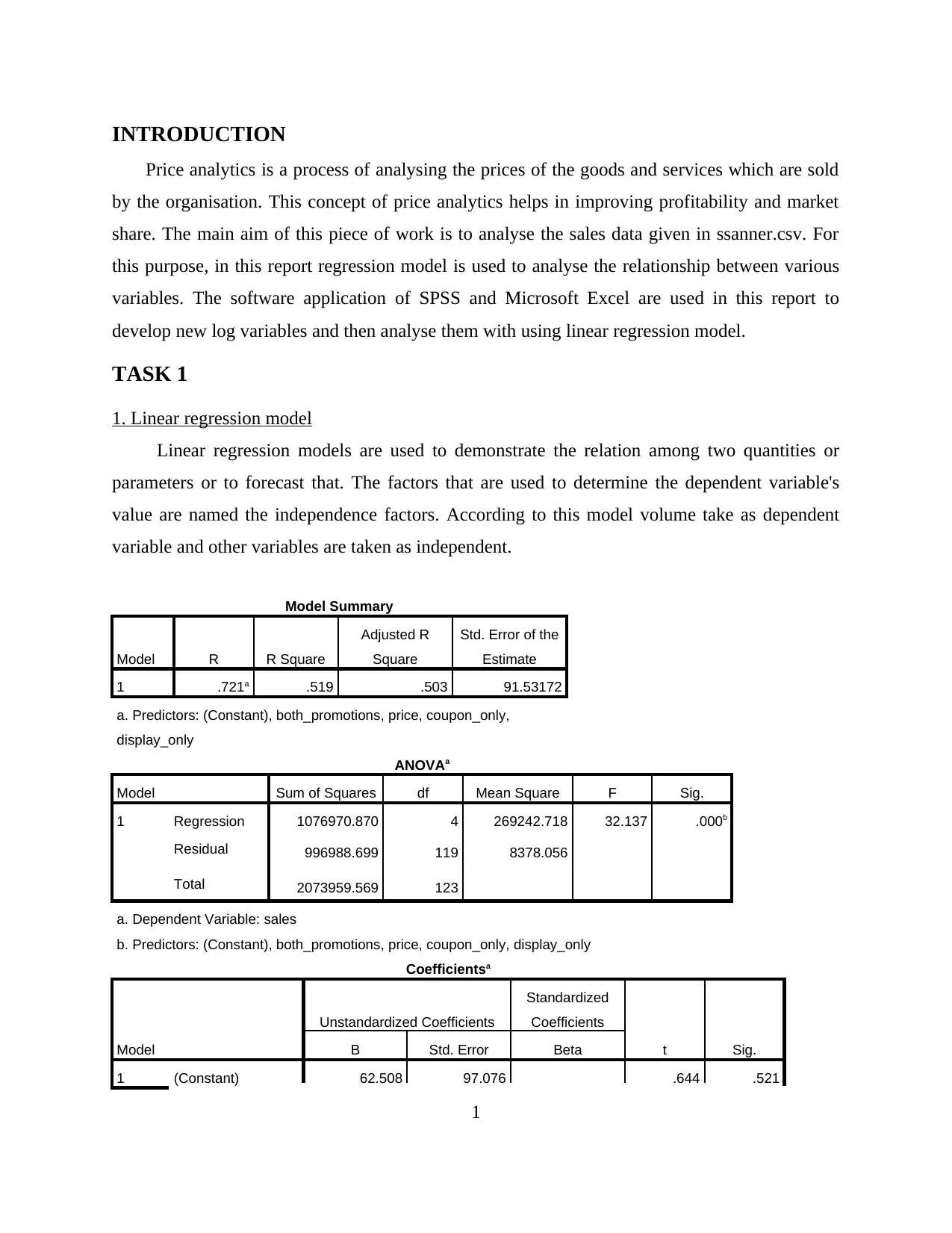
1. Linear regression model
Linear regression models are used to demonstrate the relation among two quantities or
parameters or to forecast that. The factors that are used to determine the dependent variable's
value are named the independence factors. According to this model volume take as dependent
variable and other variables are taken as independent.
Model Summary
Model R R Square
Adjusted R
Square
Std. Error of the
Estimate
1 .721a .519 .503 91.53172
a. Predictors: (Constant), both_promotions, price, coupon_only,
display_only
ANOVAa
Model Sum of Squares df Mean Square F Sig.
1 Regression 1076970.870 4 269242.718 32.137 .000b
Residual 996988.699 119 8378.056
Total 2073959.569 123
a. Dependent Variable: sales
b. Predictors: (Constant), both_promotions, price, coupon_only, display_only
Coefficientsa
Model
Unstandardized Coefficients
Standardized
Coefficients
t Sig.B Std. Error Beta
1 (Constant) 62.508 97.076 .644 .521
1

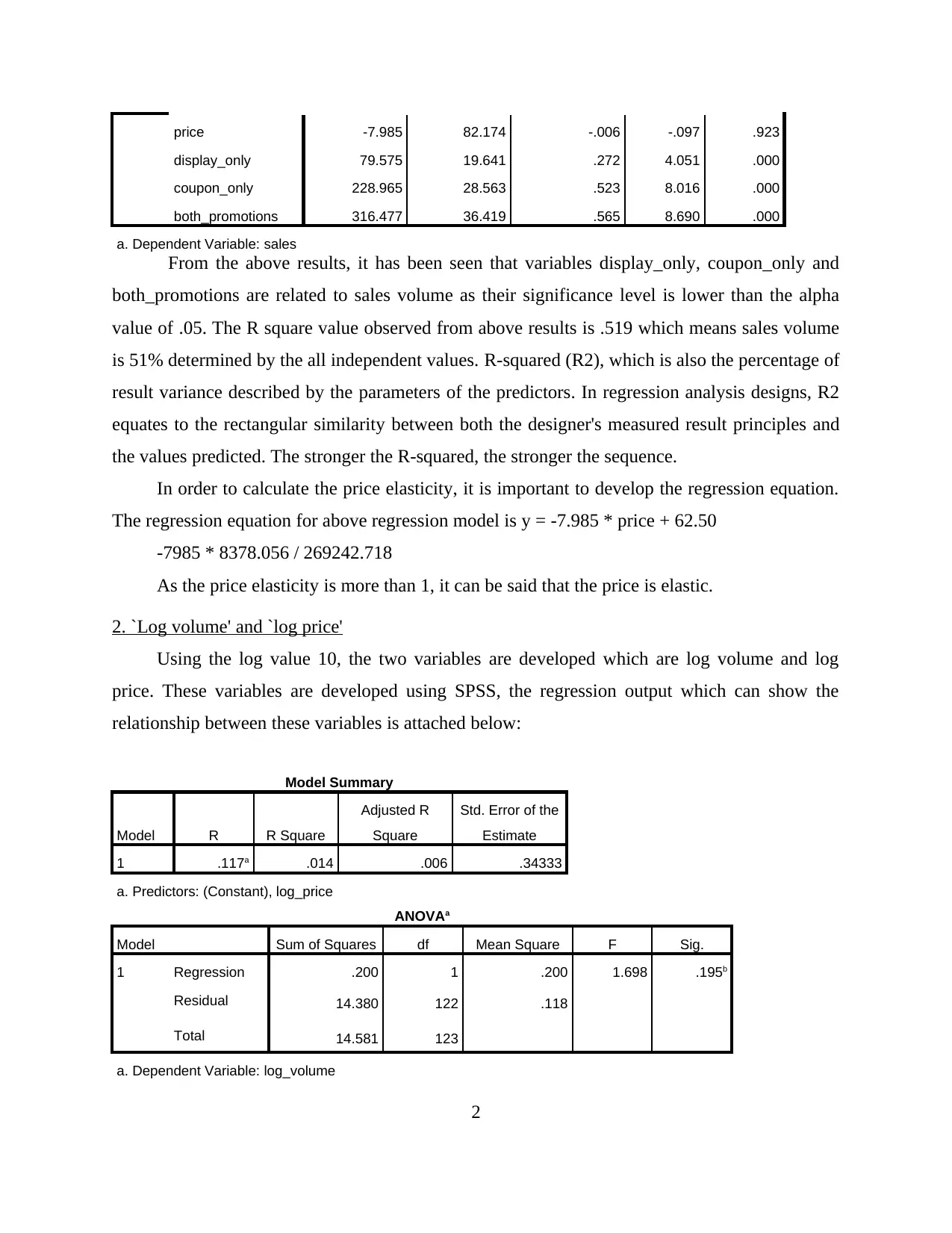
price -7.985 82.174 -.006 -.097 .923
display_only 79.575 19.641 .272 4.051 .000
coupon_only 228.965 28.563 .523 8.016 .000
both_promotions 316.477 36.419 .565 8.690 .000
a. Dependent Variable: sales
From the above results, it has been seen that variables display_only, coupon_only and
both_promotions are related to sales volume as their significance level is lower than the alpha
value of .05. The R square value observed from above results is .519 which means sales volume
is 51% determined by the all independent values. R-squared (R2), which is also the percentage of
result variance described by the parameters of the predictors. In regression analysis designs, R2
equates to the rectangular similarity between both the designer's measured result principles and
the values predicted. The stronger the R-squared, the stronger the sequence.
In order to calculate the price elasticity, it is important to develop the regression equation.
The regression equation for above regression model is y = -7.985 * price + 62.50
-7985 * 8378.056 / 269242.718
As the price elasticity is more than 1, it can be said that the price is elastic.
2. `Log volume' and `log price'
Using the log value 10, the two variables are developed which are log volume and log
price. These variables are developed using SPSS, the regression output which can show the
relationship between these variables is attached below:
Model Summary
Model R R Square
Adjusted R
Square
Std. Error of the
Estimate
1 .117a .014 .006 .34333
a. Predictors: (Constant), log_price
ANOVAa
Model Sum of Squares df Mean Square F Sig.
1 Regression .200 1 .200 1.698 .195b
Residual 14.380 122 .118
Total 14.581 123
a. Dependent Variable: log_volume
2

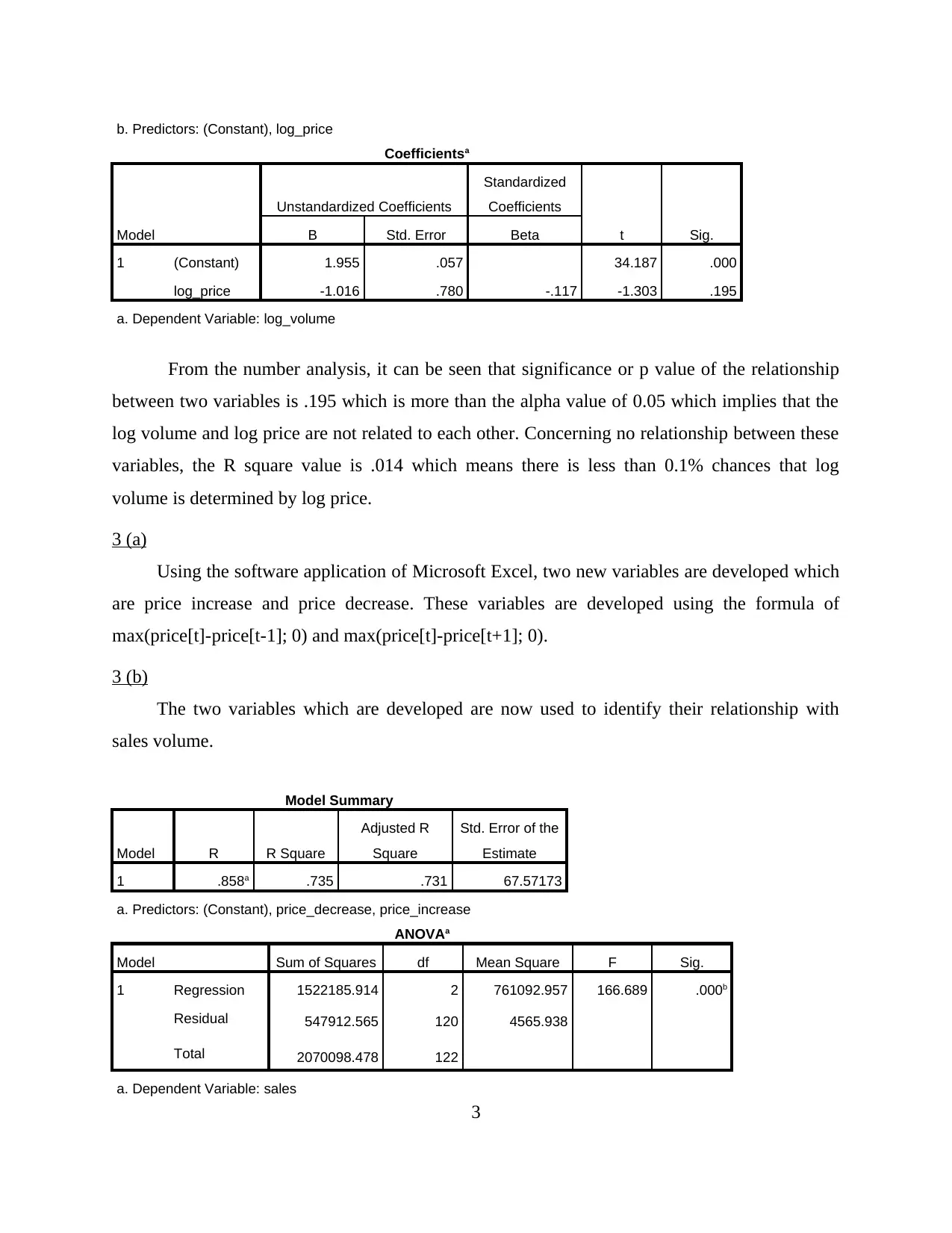
b. Predictors: (Constant), log_price
Coefficientsa
Model
Unstandardized Coefficients
Standardized
Coefficients
t Sig.B Std. Error Beta
1 (Constant) 1.955 .057 34.187 .000
log_price -1.016 .780 -.117 -1.303 .195
a. Dependent Variable: log_volume
From the number analysis, it can be seen that significance or p value of the relationship
between two variables is .195 which is more than the alpha value of 0.05 which implies that the
log volume and log price are not related to each other. Concerning no relationship between these
variables, the R square value is .014 which means there is less than 0.1% chances that log
volume is determined by log price.
3 (a)
Using the software application of Microsoft Excel, two new variables are developed which
are price increase and price decrease. These variables are developed using the formula of
max(price[t]-price[t-1]; 0) and max(price[t]-price[t+1]; 0).
3 (b)
The two variables which are developed are now used to identify their relationship with
sales volume.
Model Summary
Model R R Square
Adjusted R
Square
Std. Error of the
Estimate
1 .858a .735 .731 67.57173
a. Predictors: (Constant), price_decrease, price_increase
ANOVAa
Model Sum of Squares df Mean Square F Sig.
1 Regression 1522185.914 2 761092.957 166.689 .000b
Residual 547912.565 120 4565.938
Total 2070098.478 122
a. Dependent Variable: sales
3

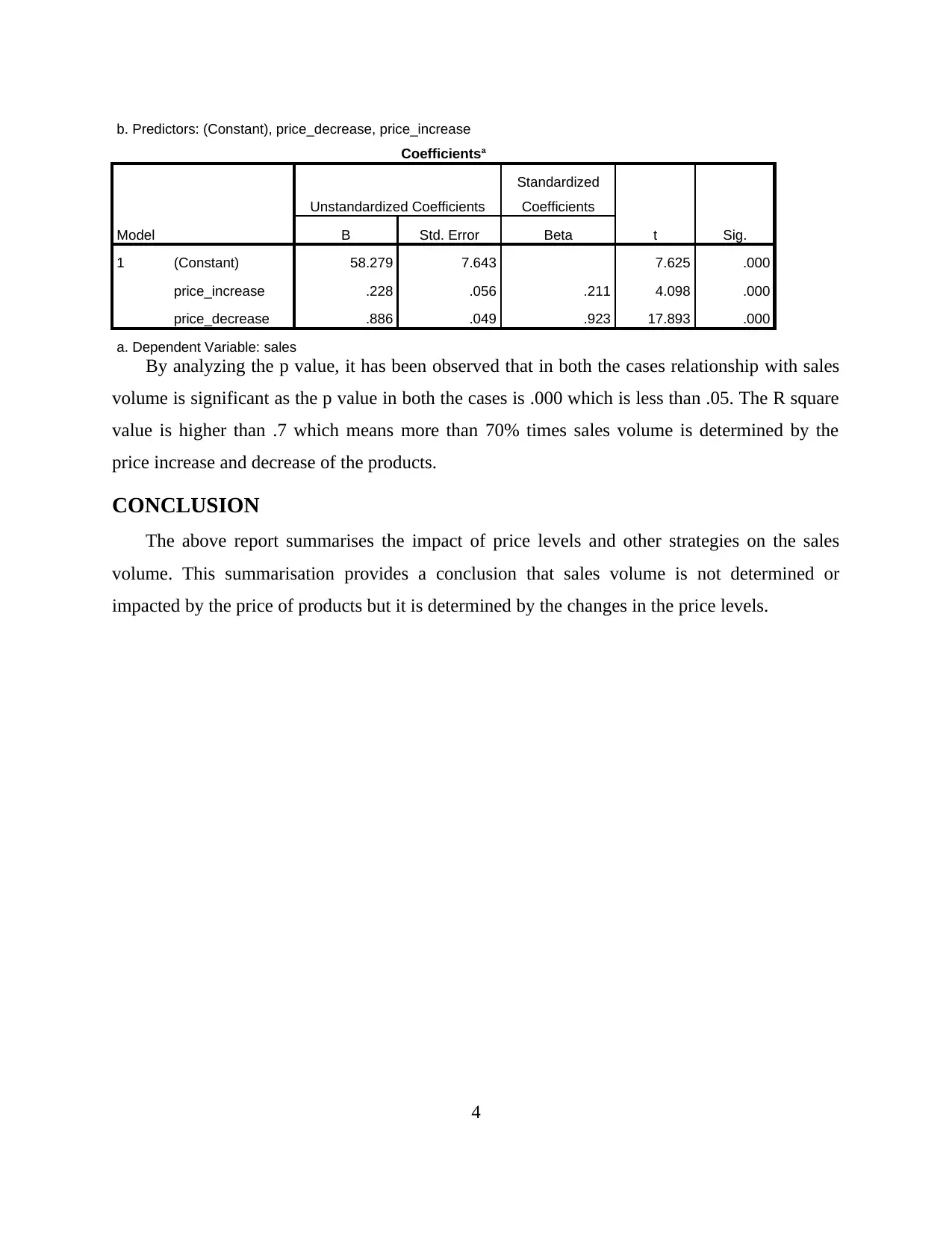
b. Predictors: (Constant), price_decrease, price_increase
Coefficientsa
Model
Unstandardized Coefficients
Standardized
Coefficients
t Sig.B Std. Error Beta
1 (Constant) 58.279 7.643 7.625 .000
price_increase .228 .056 .211 4.098 .000
price_decrease .886 .049 .923 17.893 .000
a. Dependent Variable: sales
By analyzing the p value, it has been observed that in both the cases relationship with sales
volume is significant as the p value in both the cases is .000 which is less than .05. The R square
value is higher than .7 which means more than 70% times sales volume is determined by the
price increase and decrease of the products.
CONCLUSION
The above report summarises the impact of price levels and other strategies on the sales
volume. This summarisation provides a conclusion that sales volume is not determined or
impacted by the price of products but it is determined by the changes in the price levels.
4