Chemical Engineering Assignment: Degree of Freedom and Combustion

This assignment provides detailed solutions to three chemical engineering problems. The first problem involves degree of freedom analysis of a grain drying process, including humidity calculations, mass balance, and heat input determination. The second problem focuses on the combustion of ethane and hydrogen, including calculating oxygen requirements, exhaust gas composition, and dew point. The third problem analyzes the combustion of hydrazine with excess air, determining product composition, enthalpy changes, and heat transfer requirements. Each problem includes a degree of freedom analysis to ensure the system is properly defined and solvable. Desklib offers a variety of study tools, including past papers and solved assignments, to support students in mastering these concepts.

1(a)
Degree of freedom analysis
Total number of variables = 4 streams + Q = 4(2) +1 = 9
-3 independent mass balances (air, grain, water)
-2 specifications (10 ton/day, 70 °F)
-1 pressure balance
D.O.F = 9-(3+2+1)
D.O.F =3
The humidity of the entering air at 225 °F of Dry bulb and 110 °F of Wet bulb is obtained
from the humidity chart as:
Humidity = 0.031lb H2O/ Ib dry air.
Exit air (saturated at 125°F) so,
Humidity = 0.0955 Ib H2O/ Ib dry air
Humidity of air in and air out are 0.0311b H2O/ Ib dry air and 0.0955 Ib H2O/ Ib dry air
(b) Basis: 1 hr.
Amount of wet grain =( 10 tons
day )( 1 day
24 hr )( 2000 lb
1 ton )
Water in = (0.1) (835) = 83.5 Ib/hr

Water out = (0.9)(835 lb dry grain)
1 hr * 1 lb H2 0
99 lbdry grain = 7.59 lb/hr
Amount of water removed in 1 hour = 83.5 Ib/hr - 7.59 lb/hr
= 75.9 Ib H2O/hr
(c) Product output
= (0.9)(835 lb dry grain)
1 hr + 7.59 1 lb H2 0
hr ( 24 hr
1 day ) = 7.59 lb/hr
Total product output per day = 18, 200 lb/day
(d) Begin by converting 7.59 lb/hr into lb BDA/Hr
=
7.59 Ib H 2O/hr
( 0.0955−0.0310 ) Ib H 2O
lb BDA
= 1175 lb BDA/Hr
Heat input into the drier is determined as shown below
Q = ΔH
= ΔHout – ΔHin
= (ΔHair + ΔHdrygrain + ΔHwater) – ΔHin
Enthalpy change of dry air is obtained as follows:
ΔHair = 1175lb BDA
hr [ 136.5 Btu
lb BDA − 90 Btu
lb BDA ]
= 5.46*104 Btu/hr
Enthalpy change of dry grain is obtained as follows:
ΔHdrygrain = [ ( 0.9 ) ( 835 lb dry grain )
1hr ] [ 0.18 Btu
lb ° F ]¿- 70 ° F ¿
= 0.54*104 Btu/hr
Enthalpy change of water is obtained as follows:

ΔHwater = [ 7.59 Ib H 2O
1 hr ][ 1 Btu
lb° F ] ¿- 32 ° F ¿
= 0.059*104 Btu/hr
Thus,
ΔHin = [ 83.5 Ib H 2 O
1 hr ][ 1 Btu
lb ° F ] ¿- 32 ° F ¿
= 0.32*104 Btu/hr
Substituting the above enthalpies in the equation for Q (Heat input) yields
Q = 0.32*104 Btu/hr
2)
Degree of freedom analysis
7 unknown variables (n0, n1, n2, n3, n4, n5, n6)
- 3 independent atomic species (C, H, O)
- 1 N2 balance
- 1 excess air specification (n0) as related to the fuel feed
- 1 ethane conversion specification
- 1 CO/CO2 ratio specification
D.O.F = 7 – (3+1+1+1+1)

D.O.F = 0
Let us assume the total volume of the fuel gas (C2H6 + H2) to be 1 mole.
Where, C2H6 = 0.8 mol & H2 = 0.2 mol.
O2 required for complete combustion is converted to H2O and CO2 respectively as shown
below:
0.8 C2H6 + 2.9 O2 + 0.2 H2 = 2.6 H2O + 1.6 CO2
Thus total number of moles of O2 required for total combustion is 2.9 moles.
O2 is provided in excess at 170%.
O2 present in the air = 2.9*2.7 =7.83 M
N2 present in air = 7.83*79/21 = 29.46 M
Exiting gas contains 15% CO = 0.12 moles and 80% CO2 = 0.64 moles and 5% unburnt C2H6
Balanced combustion reaction looks like
0.8 C2H6 + 4.93 O2 + 0.2 H2 + 29.46 N2 = 0.12 CO + 0.64 CO2 + 0.04 C2H6 + 6.97 O2 + 0.32
H2O + 29.46 N2
Exhaust gas composition is
Component CO CO2 C2H6 O2 H2O N2
No. of moles 0.12 0.64 0.04 6.97 0.32 29.46
Assuming only water condenses at Dew point of exhaust gas, we ignore SOx in flue gases.
Applying Borhmann / Hasse equation for flue gases
tD = [255 + 27.6 lg(pH20) + 18.7 lg(C pSO2)]
pH20 = P * XH2O = 0.32/37.55*800 = 6.81 mmHg = 8.97*10-3 atm
Since only water is able to condense,
tD = [255 + 27.6 lg(pH20)]

tD = 198.5 0C
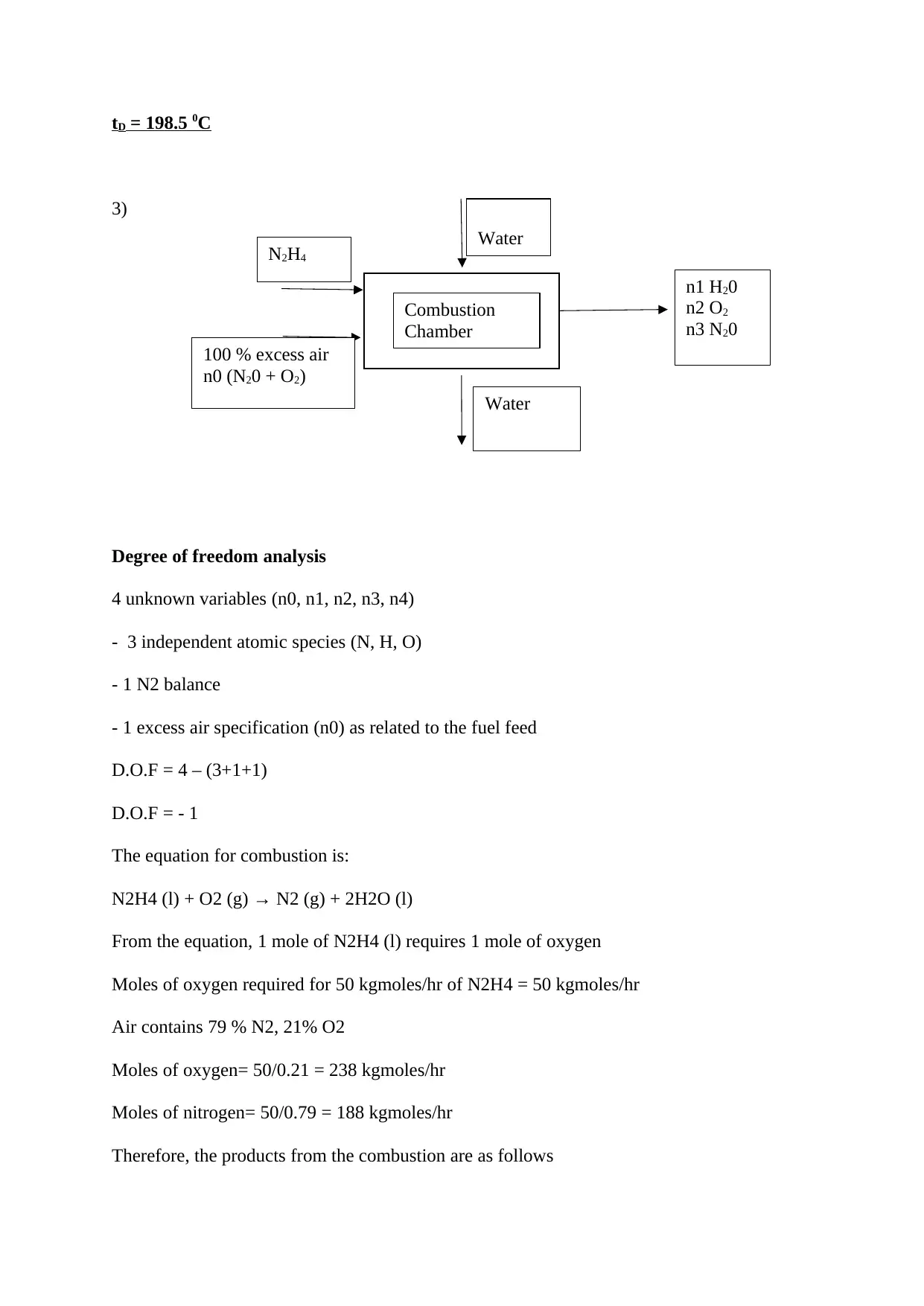
3)
Degree of freedom analysis
4 unknown variables (n0, n1, n2, n3, n4)
- 3 independent atomic species (N, H, O)
- 1 N2 balance
- 1 excess air specification (n0) as related to the fuel feed
D.O.F = 4 – (3+1+1)
D.O.F = - 1
The equation for combustion is:
N2H4 (l) + O2 (g) → N2 (g) + 2H2O (l)
From the equation, 1 mole of N2H4 (l) requires 1 mole of oxygen
Moles of oxygen required for 50 kgmoles/hr of N2H4 = 50 kgmoles/hr
Air contains 79 % N2, 21% O2
Moles of oxygen= 50/0.21 = 238 kgmoles/hr
Moles of nitrogen= 50/0.79 = 188 kgmoles/hr
Therefore, the products from the combustion are as follows
Combustion
Chamber
n1 H20
n2 O2
n3 N20
100 % excess air
n0 (N20 + O2)
Water
N2H4
Water

N2 =188 kgmoles/hr, O2 = 50 kgmoles/hr & H2O = 100 kgmoles/hr
Enthalpy of reactants:
For air CP/R = 3.355 + 0.575 * 10-3T
Change in enthalpy of air from 700K to 298K
= moles of air * ∫
298
700
CpdT
= 238 * 1000* 8.314* [(3.55*(298-700) +0.575*10-3*(2982 – 7002)/2]
= - 3.05 * 109J = - 3.05 * 109Kj/hr
Change in enthalpy of hydrazine
= mass * specific heat * (298-400)
= 50 * 44.77 * (298 – 400) Kj
= - 228,327 kJ/hr
Enthalpy of products
CP/R data
N2 = 3.280 + 0.593 * 103T
O2 = 3.639 + 0.506 * 103T
H2O = 3.470 + 1.450 * 103T
Enthalpy of N2 = 188*8.314*[3.280*(900-298) +0.593*10-3*(9002-2982)/2 =3450231 kJ/hr
Enthalpy of O2 = 50*8.314*[3.470*(900-298) +0.506*10-3*(9002-2982)/2 =944222 kJ/hr
Enthalpy of H2O =1000*8.314*[3.639*(900-298) +1.45*10-3*(9002-2982)/2 =2.25*107 kJ/hr
Total enthalpy of products = 3450231 + 944222 + 2.25*107
= 2.689 * 107 kJ/hr
Standard heat of formation: 44.77 kJ/mole
Standard heat = 44.77 *50 kJ = 2238.5 kJ/hr
Q = Enthalpy of products + enthalpy of reactants + heat of reaction
Q = 2.689* 107 +2238.5 – 223827 – 3.05* 106

Heat needed to be transferred to cooling water = 2.4 * 107 kJ/hr