Presenting Data in Table Form

This document discusses the techniques and importance of presenting data in table form. It provides examples and tips for effective data presentation. The document also includes a section on determining descriptive statistics and using the linear forecasting model for predicting values. It is a valuable resource for students studying statistics and data analysis.

PROJECT

1. Presenting data in table form..............................................................................................3
2. graphical presentation of data............................................................................................3
3. Determining descriptive statistics......................................................................................4
4. Using the linear forecasting model for predicting the value for 15 and 20 day.................8
REFERENCES.........................................................................................................................12

1. Presenting data in table form
Days Date
Sleeping Hours
per day
1 1st May 2020 5
2 2nd May 2020 8
3 3rd May 2020 6
4 4th May 2020 3
5 5th May 2020 7
6 6th May 2020 9
7 7th May 2020 4
8 8th May 2020 8
9 9th May 2020 11
10
10th May
2020 12
2. graphical presentation of data
Line graph

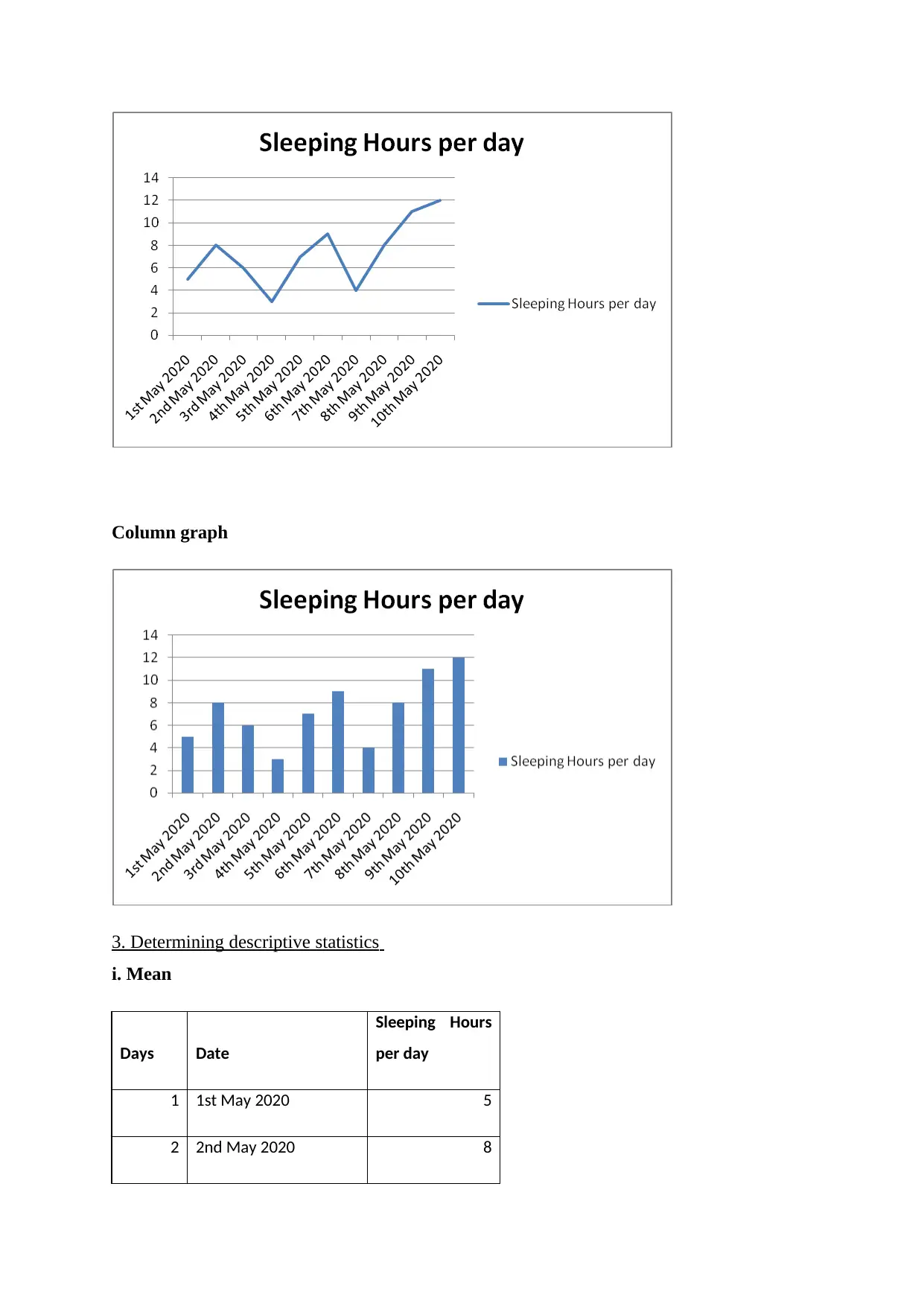
Column graph
3. Determining descriptive statistics
i. Mean
Days Date
Sleeping Hours
per day
1 1st May 2020 5
2 2nd May 2020 8

3 3rd May 2020 6
4 4th May 2020 3
5 5th May 2020 7
6 6th May 2020 9
7 7th May 2020 4
8 8th May 2020 8
9 9th May 2020 11
10 10th May 2020 12
Sum total of sleeping
hours 73
No. of observation 10
Mean 7.3
Interpretation- The above analysis reflects that the mean value resulted as 7.3 which
indicate an average sleeping hours per day (George and Mallery, 2016). It is been computed
by dividing the total of the sleeping hours with that of the total no. of an observation.
ii. Median
Step 1: Presenting data in ascending order
Days Date
Sleeping Hours
per day
1 4th May 2020 3
2 7th May 2020 4
3 1st May 2020 5
4 3rd May 2020 6

5 5th May 2020 7
6 2nd May 2020 8
7 8th May 2020 8
8 6th May 2020 9
9 9th May 2020 11
10
10th May
2020 12
No. of
observation 10
M= (10+1)/2 5.5
M= (7+8)/2 7.5
Interpretation- The result shows that the median value accounted as 7.5 hours for the
last 10 consecutive days which depicts the middle value of the sleeping hours (Mooi, Sarstedt
and Mooi-Reci, 2018). It is determined by applying the formula that is stated as (n+1)/2
which attained as 5.5 and thereafter by computing average of the 5th and 6th observation, value
of median is attained as 7.5 hours.
iii. Mode
Date
Sleeping
Hours
per day
1st May 2020 5
2nd May 2020 8
3rd May 2020 6

4th May 2020 3
5th May 2020 7
6th May 2020 9
7th May 2020 4
8th May 2020 8
9th May 2020 11
10th May
2020 12
Mode = 8
Interpretation- Mode is represented as the number of time the sleeping hours is
repeated within past 10 consecutive days. As per the analysis, the value of mode is identified
as 8 which means that 2 times in the 10 days an individual has slept for 8 hours.
iv. Range
Particulars Formula Amount
Maximum 12
Minimum 3
Range
Largest value-Smallest
value 9
Interpretation- In accordance to the assessment, the range value evaluated as 9 by
subtracting the smallest number of sleeping hours from largest sleeping hours (Mishra and
et.al., 2019). In other words it shows the difference between maximum and the minimum
hours for which an individual slept in last 10 days.
v. Standard deviation
Date Sleeping X^2

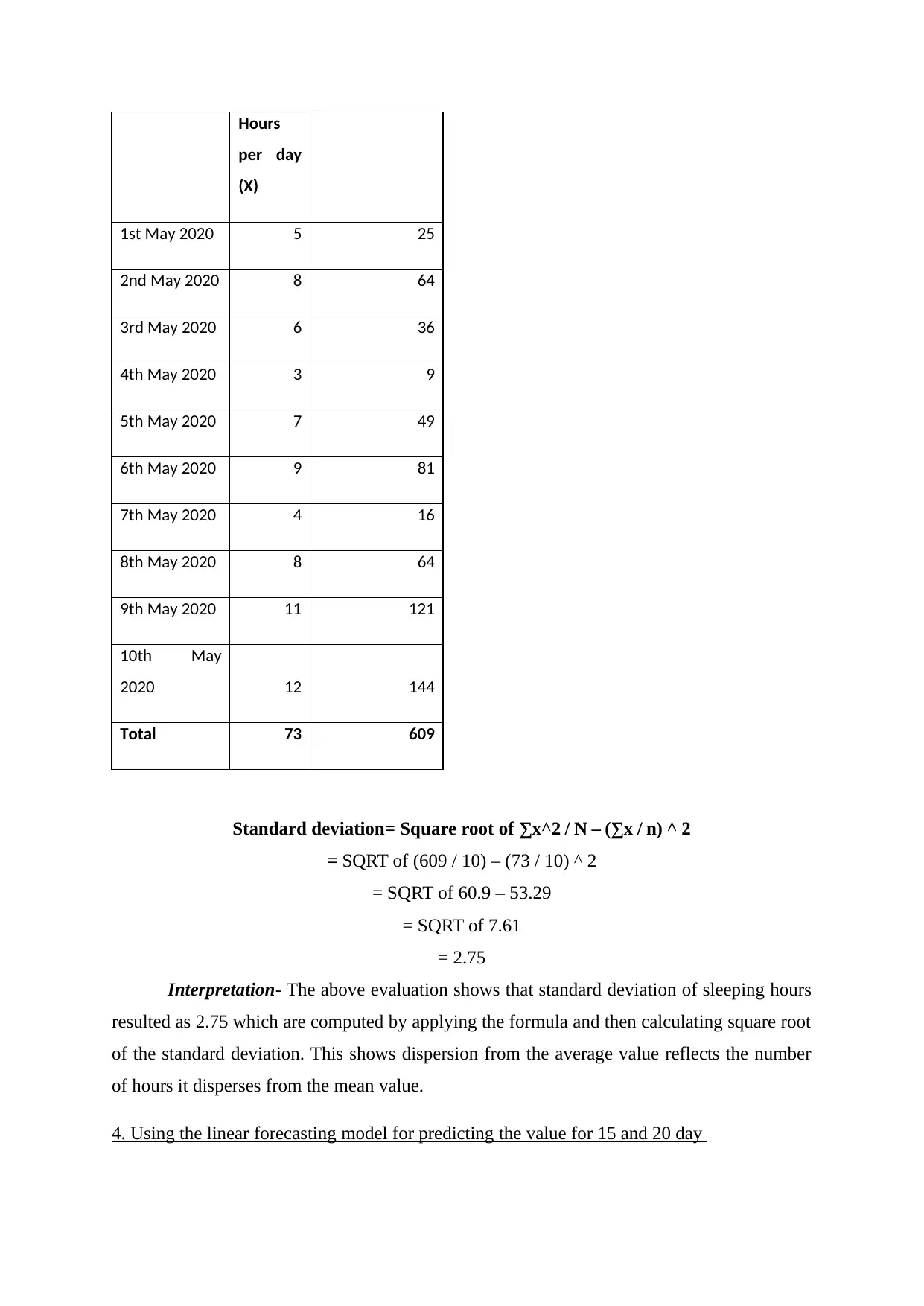
Hours
per day
(X)
1st May 2020 5 25
2nd May 2020 8 64
3rd May 2020 6 36
4th May 2020 3 9
5th May 2020 7 49
6th May 2020 9 81
7th May 2020 4 16
8th May 2020 8 64
9th May 2020 11 121
10th May
2020 12 144
Total 73 609
Standard deviation= Square root of ∑x^2 / N – (∑x / n) ^ 2
= SQRT of (609 / 10) – (73 / 10) ^ 2
= SQRT of 60.9 – 53.29
= SQRT of 7.61
= 2.75
Interpretation- The above evaluation shows that standard deviation of sleeping hours
resulted as 2.75 which are computed by applying the formula and then calculating square root
of the standard deviation. This shows dispersion from the average value reflects the number
of hours it disperses from the mean value.
4. Using the linear forecasting model for predicting the value for 15 and 20 day

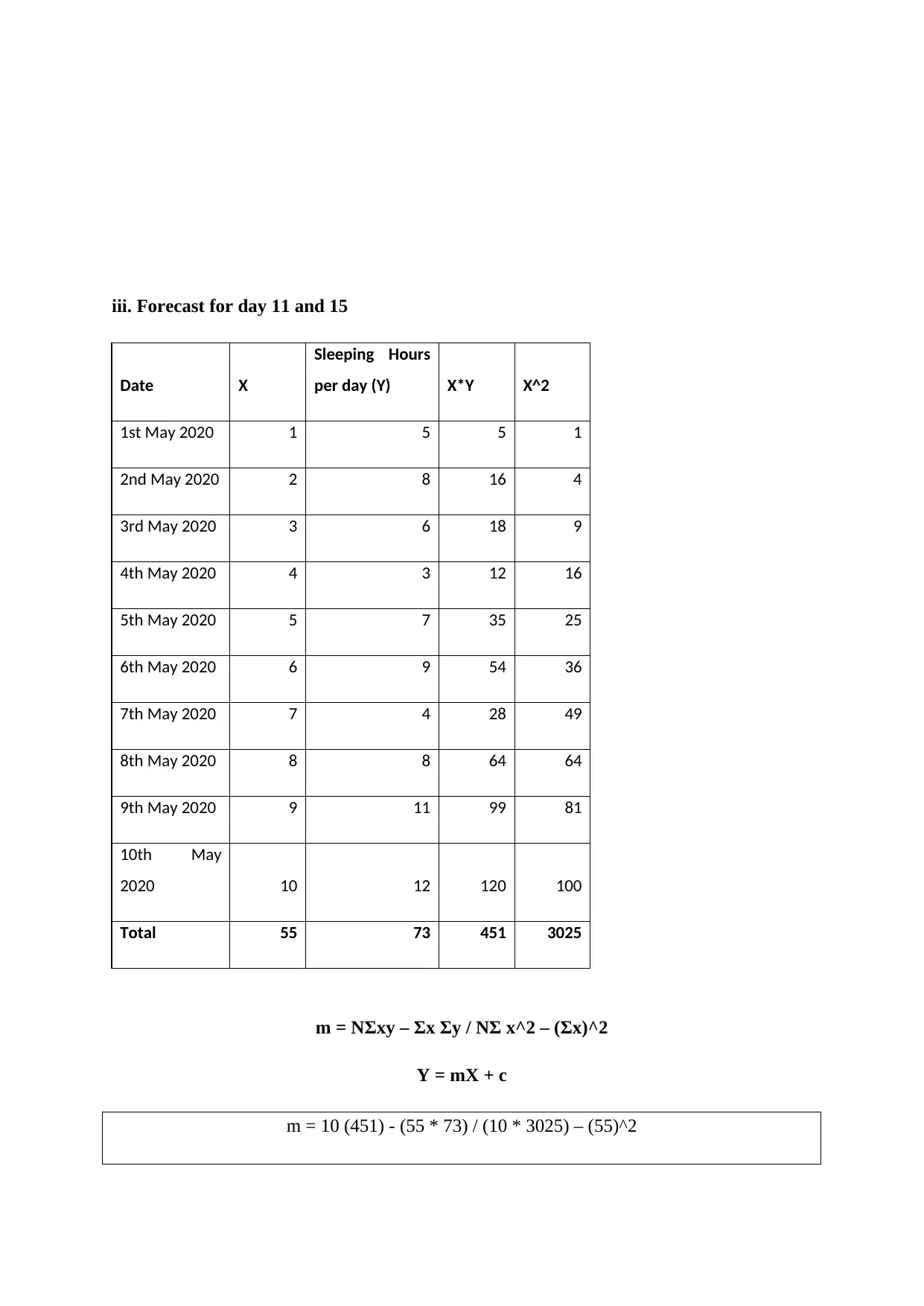
iii. Forecast for day 11 and 15
Date X
Sleeping Hours
per day (Y) X*Y X^2
1st May 2020 1 5 5 1
2nd May 2020 2 8 16 4
3rd May 2020 3 6 18 9
4th May 2020 4 3 12 16
5th May 2020 5 7 35 25
6th May 2020 6 9 54 36
7th May 2020 7 4 28 49
8th May 2020 8 8 64 64
9th May 2020 9 11 99 81
10th May
2020 10 12 120 100
Total 55 73 451 3025
m = NΣxy – Σx Σy / NΣ x^2 – (Σx)^2
Y = mX + c
m = 10 (451) - (55 * 73) / (10 * 3025) – (55)^2

m = (4510 – 4015) / (30250 – 3025)
m = 495 / 27225
m = 0.018
c = Σy – m Σx / N
c = 73 – (0.018 * 55) / 10
c = (73 – 0.99) / 10
c = 72.01 / 10
c = 7.201
Computing value of Y by making use of m and c value
For 11 days-
Y = mX + c
= 0.018(11) + (7.201)
= 0.198 + 7.201
= 7.399
For 15 days -
Y = mX + c
= 0.018(15) + (7.201)
= 0.27 + 7.201
= 7.471
Interpretation- The results shows that the value of m resulted as 0.018 and c as 7.201
by an application of the equation in an adequate manner. Moreover, by making a forecast for
11th day it has been seen that an individual will sleep for 7.399 hours and for 15th day he or
she will be sleeping for 7.47 hours (Simms and et.al., 2018). This is indicate by putting the
figures in the equation that is Y= mX + c, where x is the day for which forecast has been
made and m& c are the value that is been evaluated for solving the equation and predicting
the sleeping hours for future periods.

REFERENCES
Books and journals
George, D. and Mallery, P., 2016. Descriptive statistics. In IBM SPSS Statistics 23 Step by
Step (pp. 126-134). Routledge.
Mishra, P. and et.al., 2019. Descriptive statistics and normality tests for statistical
data. Annals of cardiac anaesthesia. 22(1). p.67.
Mooi, E., Sarstedt, M. and Mooi-Reci, I., 2018. Descriptive Statistics. In Market
Research (pp. 95-152). Springer, Singapore.
Simms, V. and et.al., 2018. Does early home environment influence basic numeracy skills?
The Preparing for Life Study. In Extending the learning from the Prevention and Early
Intervention Initiative (pp. 69-72).