Data Analysis Tools: Tables, Graphs, and Forecasting

This report explores data analysis tools such as tables, graphs, and forecasting equations. It analyzes humidity data for Cambridge, UK using these techniques. The report discusses mean, median, mode, range, and standard deviation. It also uses linear forecasting to predict future values.

PROJECT

Contents
INTRODUCTION...........................................................................................................................1
MAIN BODY..................................................................................................................................1
Arranging the data in a table format............................................................................................1
Presenting the data using charts...................................................................................................1
Calculation and discussion on the following...............................................................................2
Using the linear forecasting model to calculate the following....................................................4
CONCLUSION................................................................................................................................6
REFERENCES................................................................................................................................7

INTRODUCTION
Data analysis is a procedure of segregating, analysing, cleansing and then transforming a
data in order to get desired results (Mihas, 2019). There are various data analysis techniques
which helps an investigator to analyse its primary or secondary data which ultimately assist them
in decision making. The main aim of this report is to develop understanding about data analysis
tools. In this report, humidity data for ten consecutive for the city of Cambridge, United
Kingdom is taken in order to analyse it with the help of tables, graphs, descriptive statistical tools
and forecasting equation.
MAIN BODY
Arranging the data in a table format
Humidity data for ten days (1 December, 2019 to 10 December 2019) is taken for the city
of Cambridge, United Kingdom. The humidity data which is presented below in a table is taken
at the first hour of the day which is 06:00.
Date Humidity data (%)
01-12-19 84%
02-12-19 88%
03-12-19 90%
04-12-19 93%
05-12-19 93%
06-12-19 90%
07-12-19 92%
08-12-19 71%
09-12-19 85%
10-12-19 83%
(Source: Humidity level in Cambridge, United Kingdom, 2019)
Presenting the data using charts
The humidity data which is presented above in a table is represent below using two graphs
which are column chart and line chart.
1

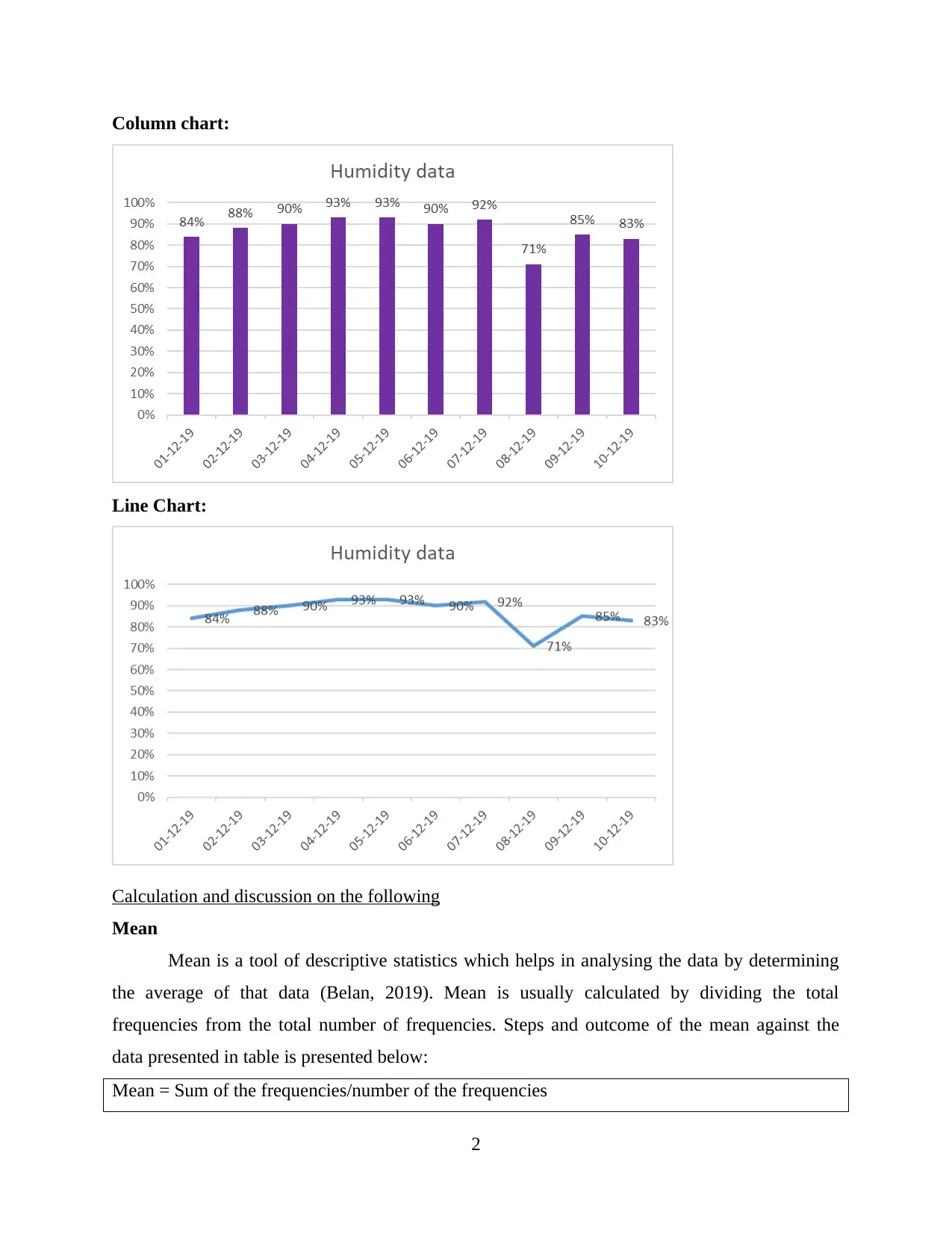
Column chart:
Line Chart:
Calculation and discussion on the following
Mean
Mean is a tool of descriptive statistics which helps in analysing the data by determining
the average of that data (Belan, 2019). Mean is usually calculated by dividing the total
frequencies from the total number of frequencies. Steps and outcome of the mean against the
data presented in table is presented below:
Mean = Sum of the frequencies/number of the frequencies
2

M = Σx/n
M = 869% /10
Mean = 87%
From the above calculation steps of mean, it is observed that Cambridge region of United
Kingdom has average humidity level of 87%.
Median
Median is the middle frequency of the data. This is a technique which helps in gaining
the middle value of the dataset. This measure is generally used to ascertain the average value
when the data include exceptionally high or low values. The steps of the calculation of median
are presented below:
Median = (n + 1)/2
= 10+1/2
= 5.5 position
Median = 91.5%
Mode
Mode is the statistical measure which shows the most recurring value from the data set. It
helps in analysing the frequency or value which is highly repeated value. In the case of small
data, it is usually calculated by simply observing the recurring value.
In the given data, there are two modes which are 90% and 93% as both of these values are
recurring two times. 90% is recurring at 3rd and 6th position. And 93% is recurring at 4th and 5th
position.
Mode = 90%, 93%
Range
Range is the area of variation between upper and lower limit from a particular data set.
This statistical measure helps in ascertaining the scope at which frequencies of the data set
varies. Range is usually calculated by comparing the maximum value of the data set from
minimum value of the data set. For the data set of humidity level for ten days, range is calculated
below:
Range = Maximum band value – Minimum band value
3

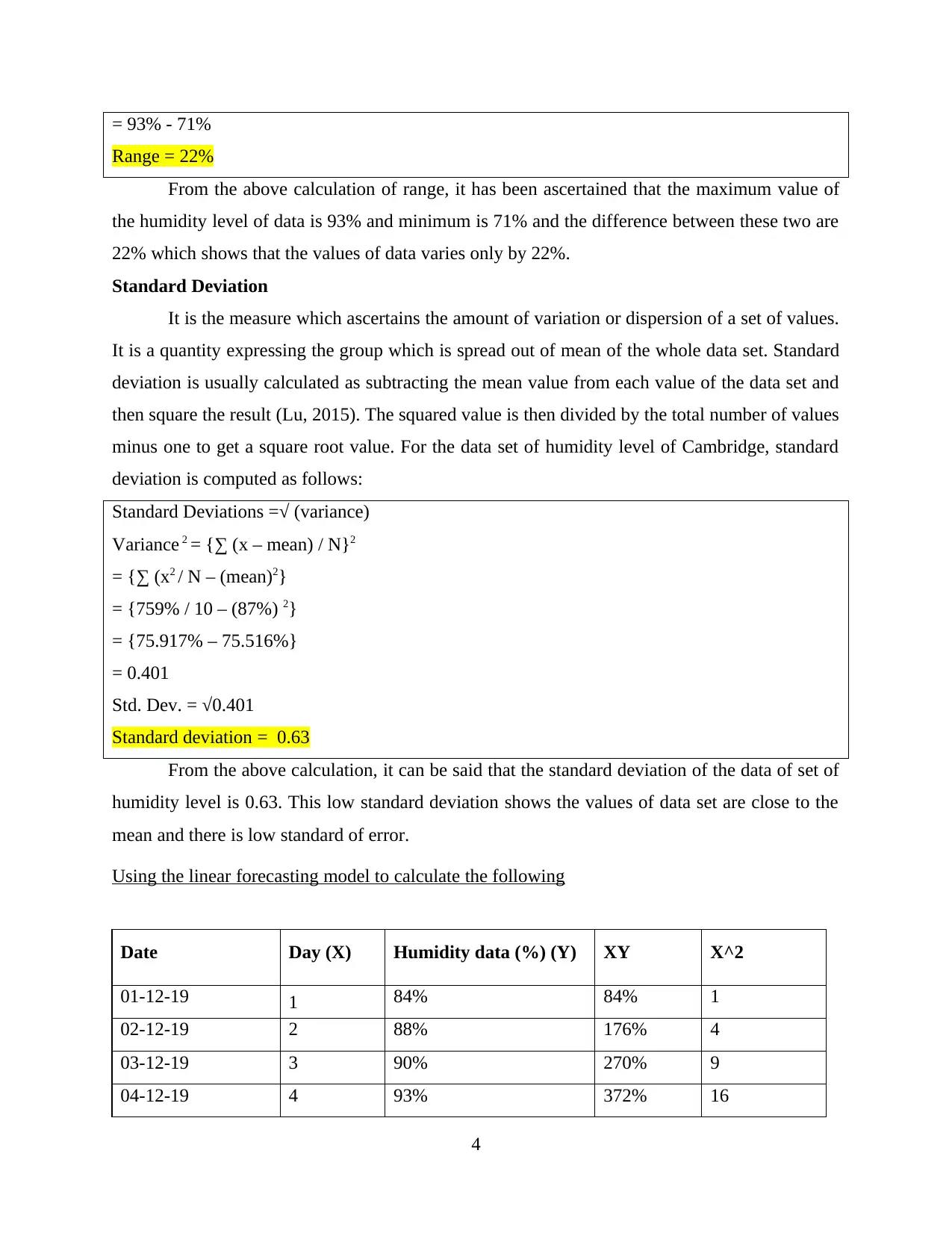
= 93% - 71%
Range = 22%
From the above calculation of range, it has been ascertained that the maximum value of
the humidity level of data is 93% and minimum is 71% and the difference between these two are
22% which shows that the values of data varies only by 22%.
Standard Deviation
It is the measure which ascertains the amount of variation or dispersion of a set of values.
It is a quantity expressing the group which is spread out of mean of the whole data set. Standard
deviation is usually calculated as subtracting the mean value from each value of the data set and
then square the result (Lu, 2015). The squared value is then divided by the total number of values
minus one to get a square root value. For the data set of humidity level of Cambridge, standard
deviation is computed as follows:
Standard Deviations =√ (variance)
Variance 2 = {∑ (x – mean) / N}2
= {∑ (x2 / N – (mean)2}
= {759% / 10 – (87%) 2}
= {75.917% – 75.516%}
= 0.401
Std. Dev. = √0.401
Standard deviation = 0.63
From the above calculation, it can be said that the standard deviation of the data of set of
humidity level is 0.63. This low standard deviation shows the values of data set are close to the
mean and there is low standard of error.
Using the linear forecasting model to calculate the following
Date Day (X) Humidity data (%) (Y) XY X^2
01-12-19 1 84% 84% 1
02-12-19 2 88% 176% 4
03-12-19 3 90% 270% 9
04-12-19 4 93% 372% 16
4

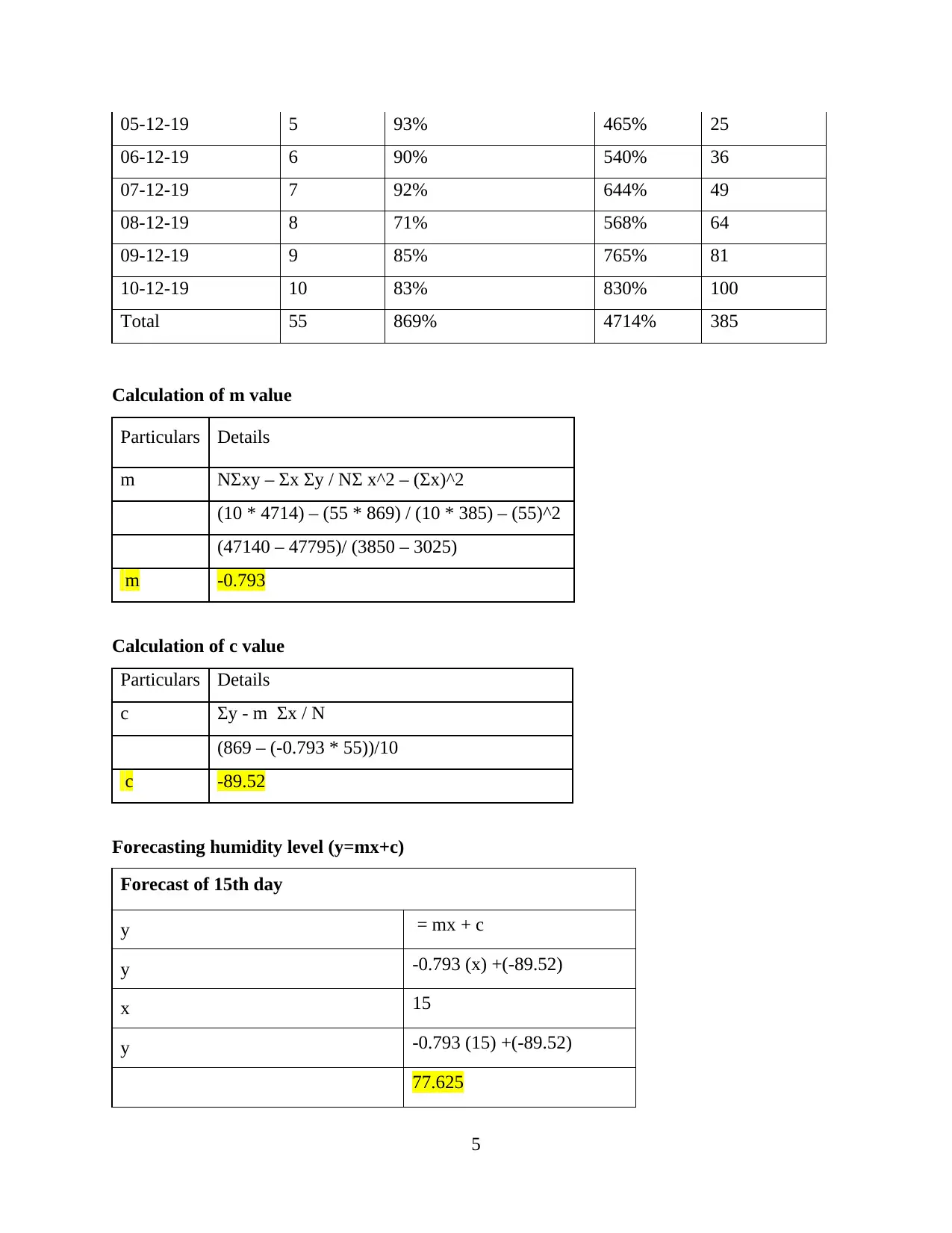
05-12-19 5 93% 465% 25
06-12-19 6 90% 540% 36
07-12-19 7 92% 644% 49
08-12-19 8 71% 568% 64
09-12-19 9 85% 765% 81
10-12-19 10 83% 830% 100
Total 55 869% 4714% 385
Calculation of m value
Particulars Details
m NΣxy – Σx Σy / NΣ x^2 – (Σx)^2
(10 * 4714) – (55 * 869) / (10 * 385) – (55)^2
(47140 – 47795)/ (3850 – 3025)
m -0.793
Calculation of c value
Particulars Details
c Σy - m Σx / N
(869 – (-0.793 * 55))/10
c -89.52
Forecasting humidity level (y=mx+c)
Forecast of 15th day
y = mx + c
y -0.793 (x) +(-89.52)
x 15
y -0.793 (15) +(-89.52)
77.625
5

Forecast of 20th day
y = mx + c
y -0.793 (x) +89.52
x 20
y 0.793 (20) +89.52
73.66
The linear equation of y=mx+c is used to forecast future values by using a linear data set
(Dong, Sun and Li, 2017). In this case, data set of humidity level is used in which humidity level
of 10 days is used, from which humidity level of day 15th and 20th is calculated. Humidity level
in Cambridge, UK for the 15 day or 15 December, 2019 is 77.625% and 73.66% for 20th day.
CONCLUSION
From the above report, it has been concluded that data analysis can be used to analyse the
data by using statistical tools. It has been observed that tools of forecasting, mean, mode, median
standard deviation etc. can help an investigator to get desired result from the data.
6

REFERENCES
Books and Journals
Belan, S., 2019. Median and Mode in First Passage under Restart. arXiv preprint
arXiv:1906.05619.
Dong, Q., Sun, Y. and Li, P., 2017. A novel forecasting model based on a hybrid processing
strategy and an optimized local linear fuzzy neural network to make wind power
forecasting: A case study of wind farms in China. Renewable Energy. 102. pp.241-257.
Lu, J., Microsoft Technology Licensing LLC, 2015. Iteratively calculating standard deviation for
streamed data. U.S. Patent 9,069,726.
Mihas, P., 2019. Qualitative data analysis. In Oxford Research Encyclopedia of Education.
Online
Humidity level in Cambridge, United Kingdom. 2019. [Online]. Available through:
<https://www.worldweatheronline.com/cambridge-weather-history/cambridgeshire/
gb.aspx>
7