Numeracy and Data Analysis

This study report explores the key elements of data analysis using the selected data of money spent on transport. It covers the arrangement of expenses data in a tabular format, presenting the data using two different types of charts, calculations and discussions on mean, median, mode, range, and standard deviation, and the use of a linear forecasting model to predict future spending.

Numeracy and Data Analysis

Contents
INTRODUCTION...........................................................................................................................3
MAIN BODY...................................................................................................................................3
1. Arrangement of expenses data in tabular format:.............................................................3
2. Presenting the above data using two different types of charts:........................................3
3. Calculations and discussion of following:..........................................................................4
4. Linear forecasting model that is “y = mx + c” to calculate and discuss the followings:....6
CONCLUSION................................................................................................................................7
REFERENCES................................................................................................................................9

INTRODUCTION
Data analysis relates to processes or mechanism of organizing, transforming, and
evaluating raw data/facts in order to obtain actionable, useful information that can assist
companies in making informed decisions. Through offering valuable observations and facts,
which are also provided in maps, photographs, tables, and diagrams, the technique helps to
decrease the risks associated with decision-making (Fagerland, Lydersen and Laake, 2017). The
study-report explores different key element is data analysis using the selected data of money
spend on transport during ten consecutive months. The study analyse data using mean approach,
median and mode, Standard deviation formula as well as linear forecasting model.
MAIN BODY
1. Arrangement of expenses data in tabular format:
Month Amount of money spent on transport
(in GBP)
Jan. 120
Feb. 170
Mar. 140
Apr. 170
May 210
June 120
July 190
Aug. 180
Sep. 220
Oct. 100
2. Presenting the above data using two different types of charts:
Line Chart: This is chart wherein broken line connects points describing variable values to
appropriate values of independent variable (Xia and Sun, 2017).

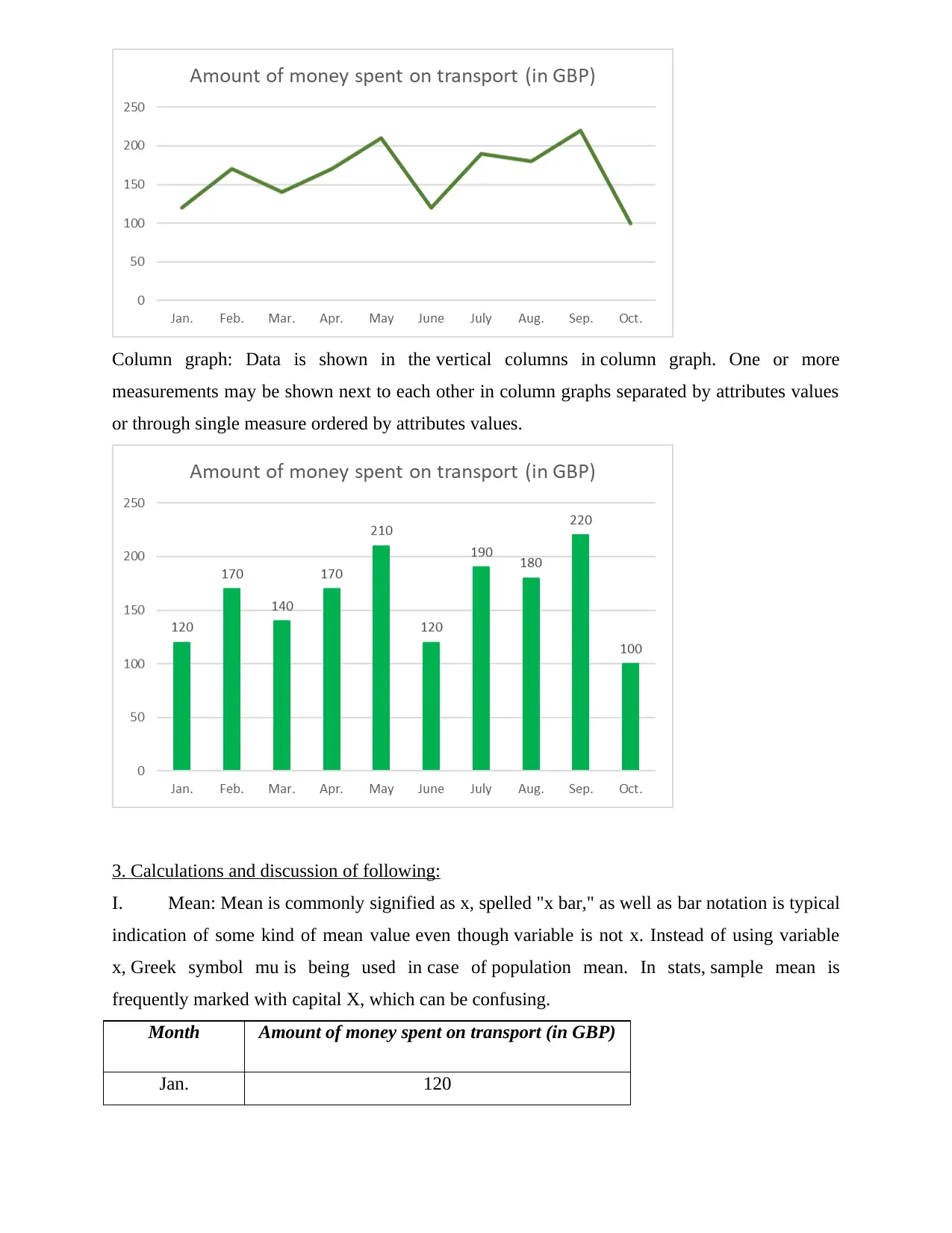
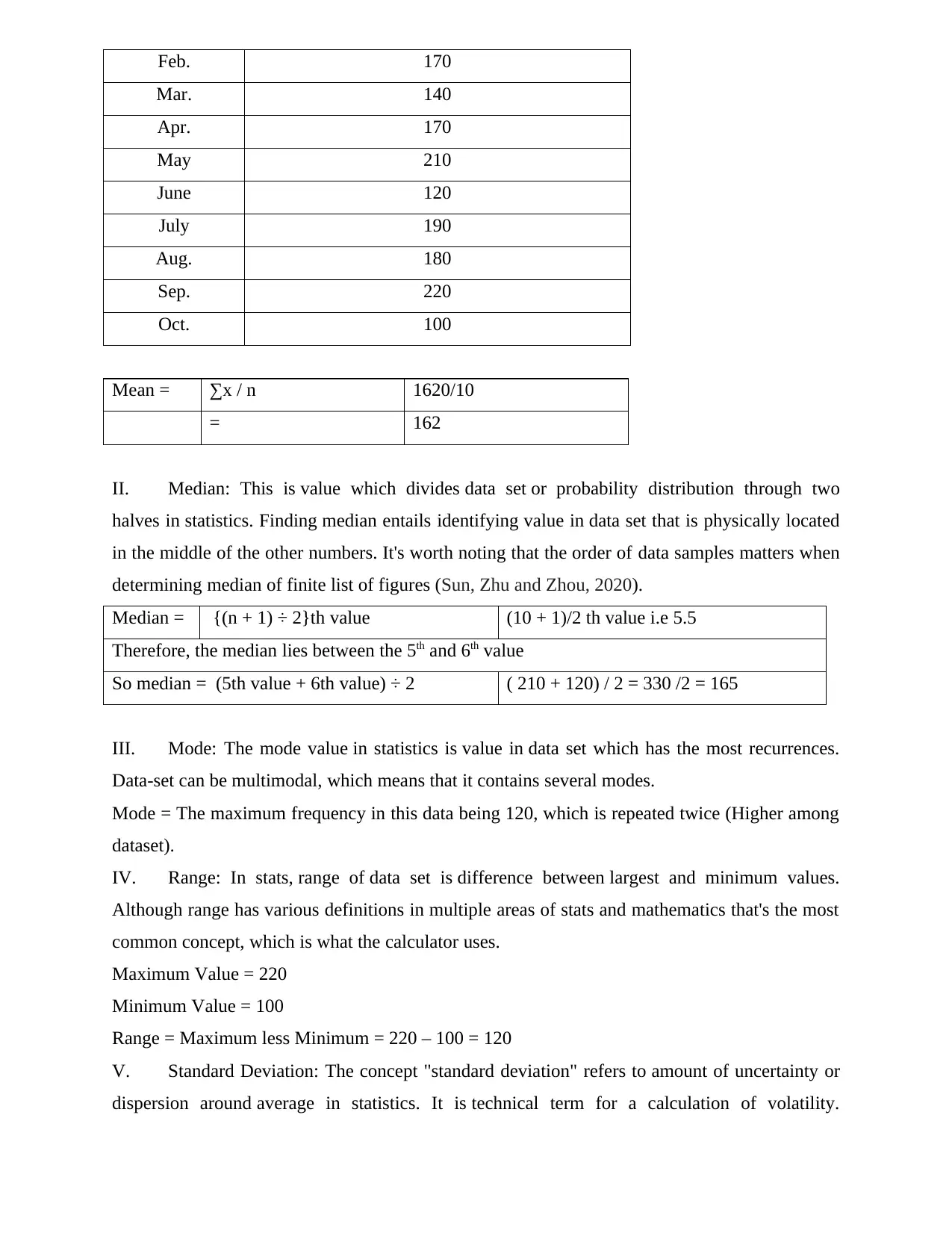
Column graph: Data is shown in the vertical columns in column graph. One or more
measurements may be shown next to each other in column graphs separated by attributes values
or through single measure ordered by attributes values.
3. Calculations and discussion of following:
I. Mean: Mean is commonly signified as x, spelled "x bar," as well as bar notation is typical
indication of some kind of mean value even though variable is not x. Instead of using variable
x, Greek symbol mu is being used in case of population mean. In stats, sample mean is
frequently marked with capital X, which can be confusing.
Month Amount of money spent on transport (in GBP)
Jan. 120

Feb. 170
Mar. 140
Apr. 170
May 210
June 120
July 190
Aug. 180
Sep. 220
Oct. 100
Mean = ∑x / n 1620/10
= 162
II. Median: This is value which divides data set or probability distribution through two
halves in statistics. Finding median entails identifying value in data set that is physically located
in the middle of the other numbers. It's worth noting that the order of data samples matters when
determining median of finite list of figures (Sun, Zhu and Zhou, 2020).
Median = {(n + 1) ÷ 2}th value (10 + 1)/2 th value i.e 5.5
Therefore, the median lies between the 5th and 6th value
So median = (5th value + 6th value) ÷ 2 ( 210 + 120) / 2 = 330 /2 = 165
III. Mode: The mode value in statistics is value in data set which has the most recurrences.
Data-set can be multimodal, which means that it contains several modes.
Mode = The maximum frequency in this data being 120, which is repeated twice (Higher among
dataset).
IV. Range: In stats, range of data set is difference between largest and minimum values.
Although range has various definitions in multiple areas of stats and mathematics that's the most
common concept, which is what the calculator uses.
Maximum Value = 220
Minimum Value = 100
Range = Maximum less Minimum = 220 – 100 = 120
V. Standard Deviation: The concept "standard deviation" refers to amount of uncertainty or
dispersion around average in statistics. It is technical term for a calculation of volatility.

Disparity between actual versus average figure is known as dispersion. Standard deviation
increases as dispersion or uncertainty increases (Little and Rubin, 2019).
Months Amount of money you spend on
transport (in GBP)
x- x̄ (x- x̄)^2
January 120 -42 1764
February 170 8 64
March 140 -22 484
April 170 8 64
May 210 48 2304
June 120 -42 1764
July 190 28 784
August 180 18 324
September 220 58 3364
October 100 -62 3844
x̄ = ∑x / n = 162 ∑(x- x̄)^2 = 14760
Standard Deviation = √[∑(x- x̄)^2]/n = 14760 /10 = 1476 38.41875
4. Linear forecasting model that is “y = mx + c” to calculate and discuss the followings:
Day (x) Amount of money you spend on
transport (y) xy x^2
1 120 120 1
2 170 340 4
3 140 420 9
4 170 680 16
5 210 1050 25
6 120 720 36
7 190 1330 49
8 180 1440 64
9 220 1980 81
10 100 1000 100

∑x = 55 ∑y = 1620 ∑xy = 9080
∑x^2 =
385
Steps to calculate m value:
m= n (∑xy) - (∑x) (∑y)/ n(∑x2) - (∑x)2
m = 10 * 9080 - 55 * 1620 / 10 * 385 - 55*55
m = 90800 - 89100/ 3850 - 3025
m = 1700 / 825
m = 2.06
Steps to calculate c value:
C= [(∑y) / n]-m(∑x/n)
c = (1620 / 10) - (2.06 * 55/10)
c = 162 + 11.33
c = 172.33
Forecasting the spending towards transport for month 14 and month 16:
Forecasting for month 14:
y= mx + c
y = 2.06 * 14 + 173.33
y = 202.17
Forecasting for month 16:
y = mx + c
y = 2.06 * 16 + 172.33
y = 205.29
CONCLUSION
Form above study this has been ascertained that Data analysis findings must be presented
in a way that the users need in order to support decisions and actions. Additional analysis could
be required as a result of user’s feedback. Data analysts may use data analysis tools including
tables and graphs to support users understand the message more easily and effectively. The

research tools allow to highlight important details in figures and charts using color coding and
formatting. The data would've been ready for review after it had been processed, arranged,
including cleaned. To recognize, analyze, and draw conclusions cantered on requirements a
variety of data analysis approaches are accessible Data visualization can also be applied to
evaluate data in graphical context in order to gain more insight into the data's communications.

REFERENCES
Books and Journals:
Fagerland, M., Lydersen, S. and Laake, P., 2017. Statistical analysis of contingency tables. CRC
press.
Xia, Y. and Sun, J., 2017. Hypothesis testing and statistical analysis of microbiome. Genes &
diseases, 4(3), pp.138-148.
Sun, S., Zhu, J. and Zhou, X., 2020. Statistical analysis of spatial expression patterns for spatially
resolved transcriptomic studies. Nature methods, 17(2), pp.193-200.
Little, R.J. and Rubin, D.B., 2019. Statistical analysis with missing data (Vol. 793). John Wiley
& Sons.