Risk Management Model for Desklib - Analysis of CAPM, Systematic Risk, Alpha, Validity of Model, Sharpe Measure and Treynor Measure
VerifiedAdded on 2022/11/14
|12
|2237
|330
AI Summary
The Risk Management Model for Desklib includes analysis of CAPM, Systematic Risk, Alpha, Validity of Model, Sharpe Measure and Treynor Measure. It covers portfolio return, required rate of return, and risk adjusted performance of assets. The report also provides insights on the interpretation of R2 and the comparison among the results.
Contribute Materials
Your contribution can guide someone’s learning journey. Share your
documents today.

Running Head: Risk Management Model
1
Project Report: Risk Management Model
1
Project Report: Risk Management Model
Secure Best Marks with AI Grader
Need help grading? Try our AI Grader for instant feedback on your assignments.

Risk Management Model
2
Contents
Task 1................................................................................................................................3
a) CAPM.......................................................................................................................3
b) Portfolio Return........................................................................................................3
Task 2................................................................................................................................3
Systematic risk..............................................................................................................3
Alpha.............................................................................................................................4
Validity of model..........................................................................................................4
Interpretation of R2.......................................................................................................6
Required rate of return..................................................................................................6
Task 3................................................................................................................................7
Sharpe measure and Treynor Measure of single asset..................................................7
Sharpe measure and Treynor Measure of portfolio asset.............................................8
Comparison among the results......................................................................................9
References:.....................................................................................................................10
Appendix.........................................................................................................................11
2
Contents
Task 1................................................................................................................................3
a) CAPM.......................................................................................................................3
b) Portfolio Return........................................................................................................3
Task 2................................................................................................................................3
Systematic risk..............................................................................................................3
Alpha.............................................................................................................................4
Validity of model..........................................................................................................4
Interpretation of R2.......................................................................................................6
Required rate of return..................................................................................................6
Task 3................................................................................................................................7
Sharpe measure and Treynor Measure of single asset..................................................7
Sharpe measure and Treynor Measure of portfolio asset.............................................8
Comparison among the results......................................................................................9
References:.....................................................................................................................10
Appendix.........................................................................................................................11
Risk Management Model
3
Task 1:
a) CAPM:
Below are the returns from all the three assets:
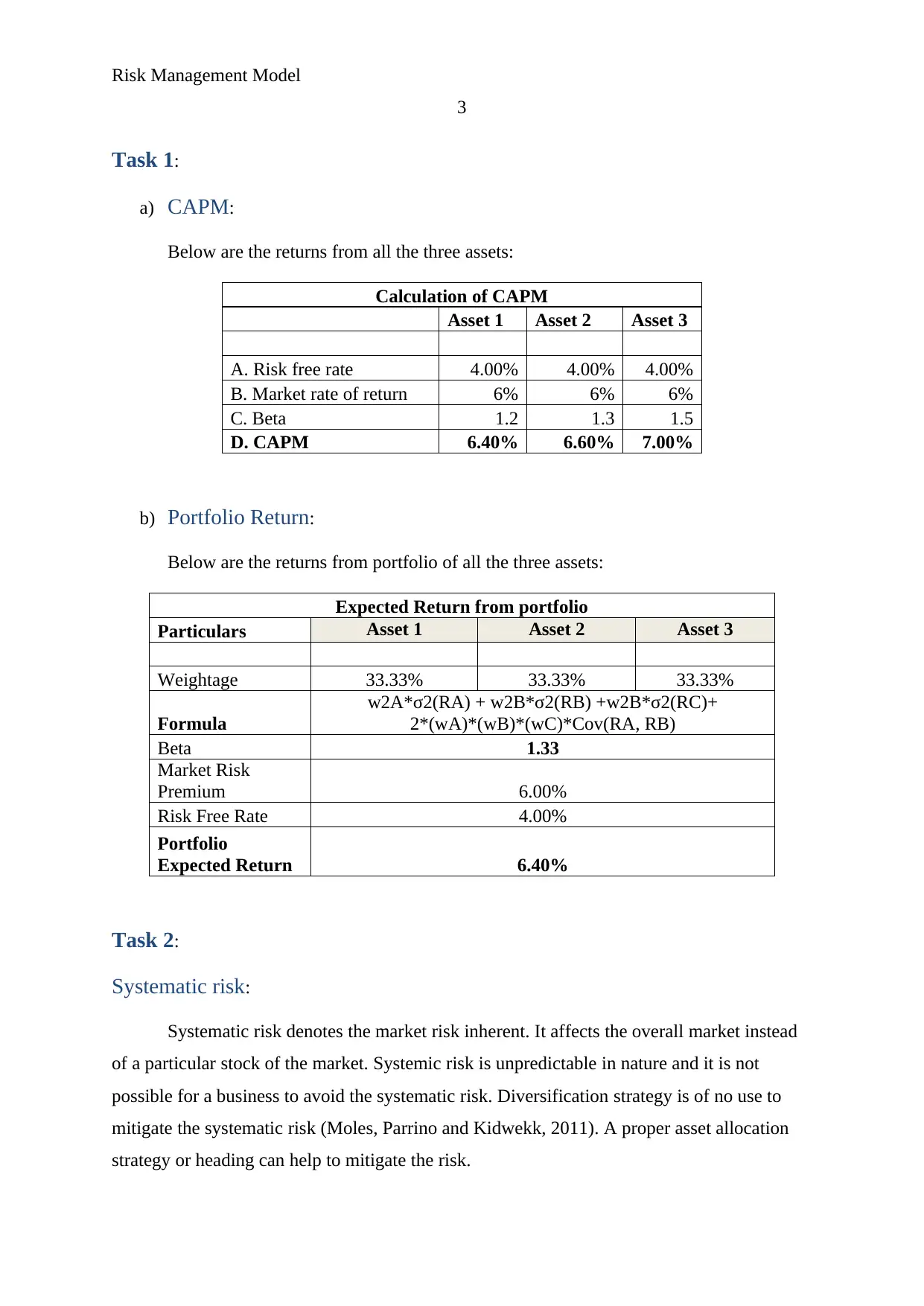
Calculation of CAPM
Asset 1 Asset 2 Asset 3
A. Risk free rate 4.00% 4.00% 4.00%
B. Market rate of return 6% 6% 6%
C. Beta 1.2 1.3 1.5
D. CAPM 6.40% 6.60% 7.00%
b) Portfolio Return:
Below are the returns from portfolio of all the three assets:
Expected Return from portfolio
Particulars Asset 1 Asset 2 Asset 3
Weightage 33.33% 33.33% 33.33%
Formula
w2A*σ2(RA) + w2B*σ2(RB) +w2B*σ2(RC)+
2*(wA)*(wB)*(wC)*Cov(RA, RB)
Beta 1.33
Market Risk
Premium 6.00%
Risk Free Rate 4.00%
Portfolio
Expected Return 6.40%
Task 2:
Systematic risk:
Systematic risk denotes the market risk inherent. It affects the overall market instead
of a particular stock of the market. Systemic risk is unpredictable in nature and it is not
possible for a business to avoid the systematic risk. Diversification strategy is of no use to
mitigate the systematic risk (Moles, Parrino and Kidwekk, 2011). A proper asset allocation
strategy or heading can help to mitigate the risk.
3
Task 1:
a) CAPM:
Below are the returns from all the three assets:
Calculation of CAPM
Asset 1 Asset 2 Asset 3
A. Risk free rate 4.00% 4.00% 4.00%
B. Market rate of return 6% 6% 6%
C. Beta 1.2 1.3 1.5
D. CAPM 6.40% 6.60% 7.00%
b) Portfolio Return:
Below are the returns from portfolio of all the three assets:
Expected Return from portfolio
Particulars Asset 1 Asset 2 Asset 3
Weightage 33.33% 33.33% 33.33%
Formula
w2A*σ2(RA) + w2B*σ2(RB) +w2B*σ2(RC)+
2*(wA)*(wB)*(wC)*Cov(RA, RB)
Beta 1.33
Market Risk
Premium 6.00%
Risk Free Rate 4.00%
Portfolio
Expected Return 6.40%
Task 2:
Systematic risk:
Systematic risk denotes the market risk inherent. It affects the overall market instead
of a particular stock of the market. Systemic risk is unpredictable in nature and it is not
possible for a business to avoid the systematic risk. Diversification strategy is of no use to
mitigate the systematic risk (Moles, Parrino and Kidwekk, 2011). A proper asset allocation
strategy or heading can help to mitigate the risk.
Risk Management Model
4
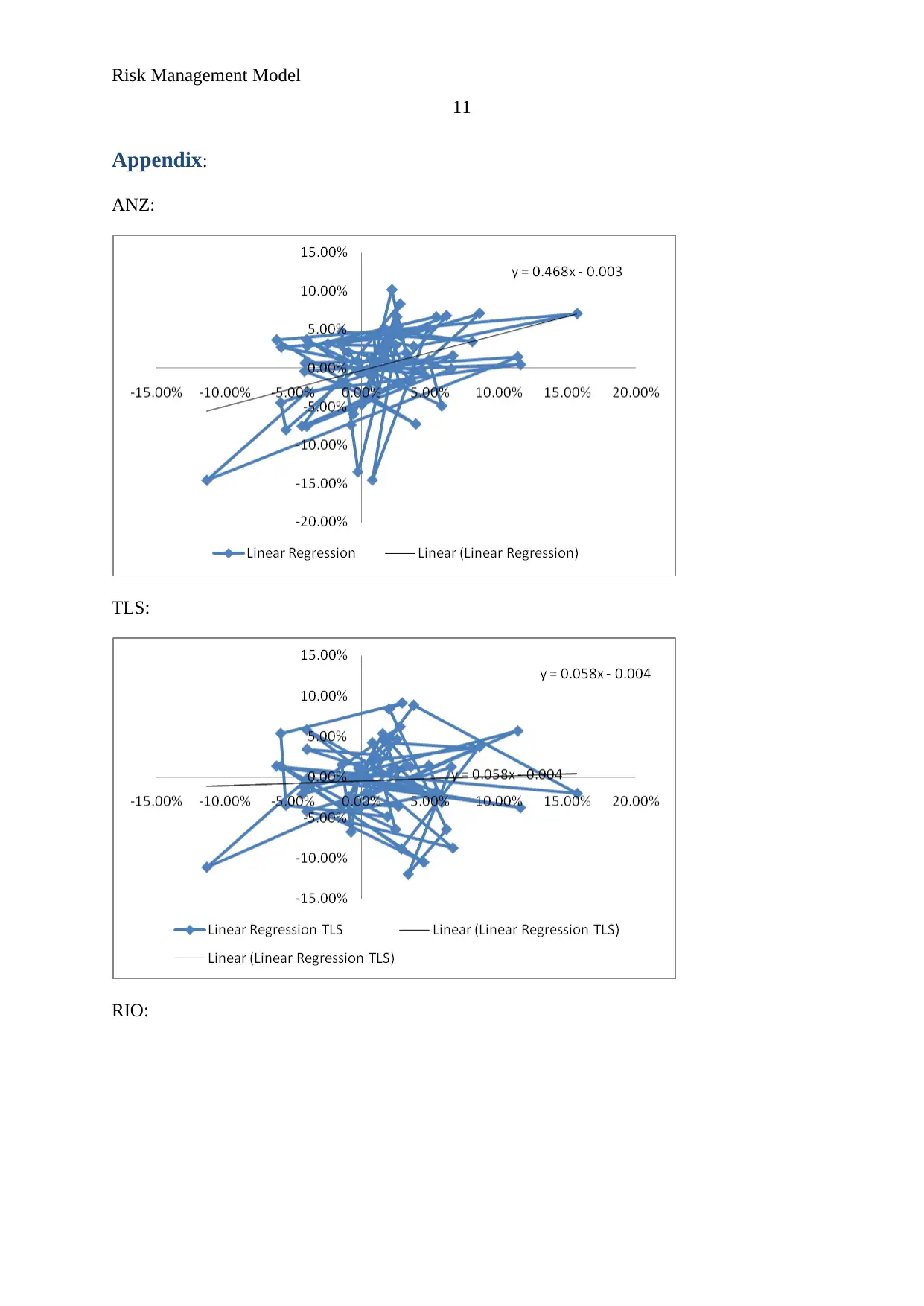
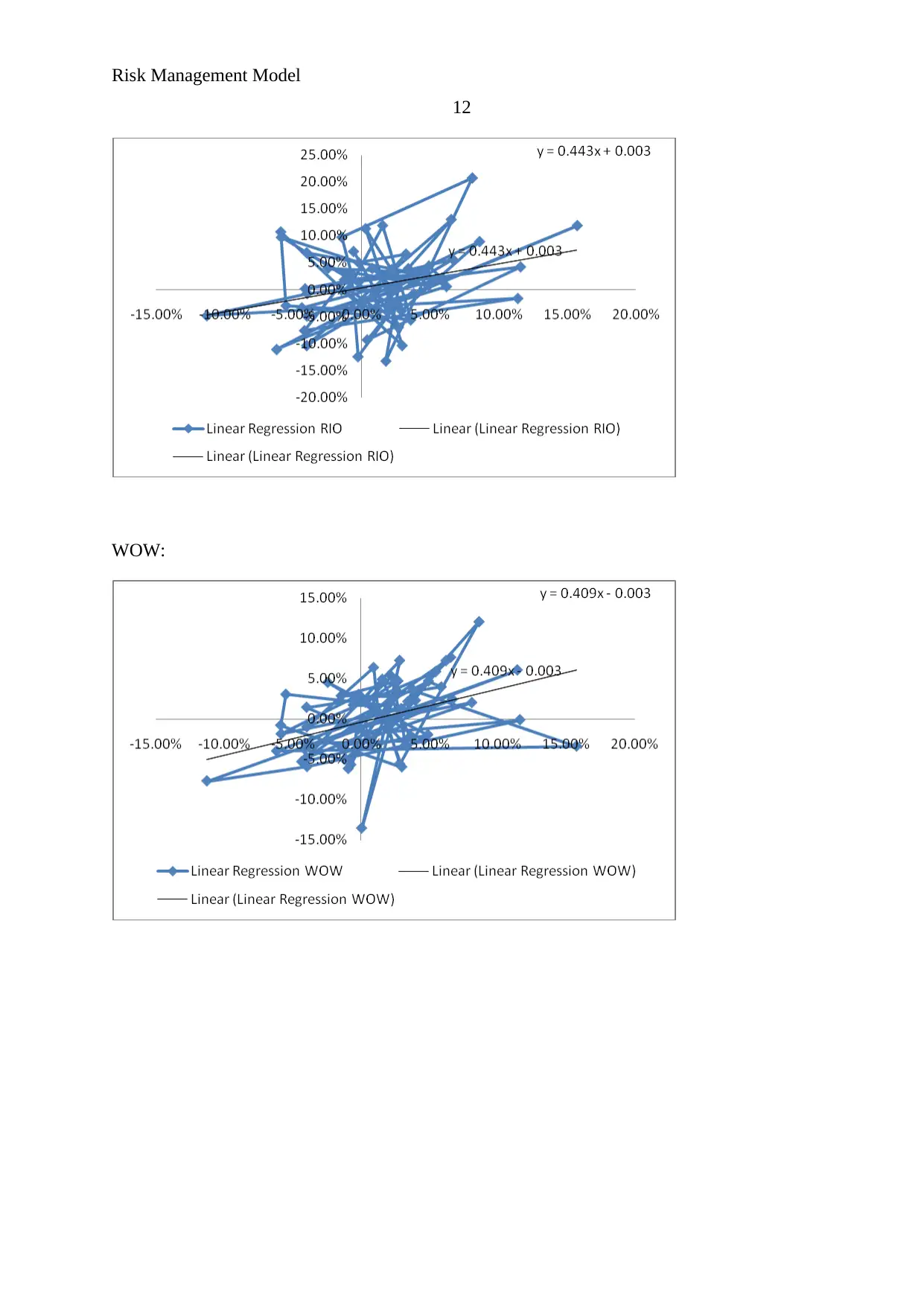
In the case of ANZ, TLS, RIO and WOW, it has been measured that the systematic
risk of all the four assets are different. Below is the information of Beta:
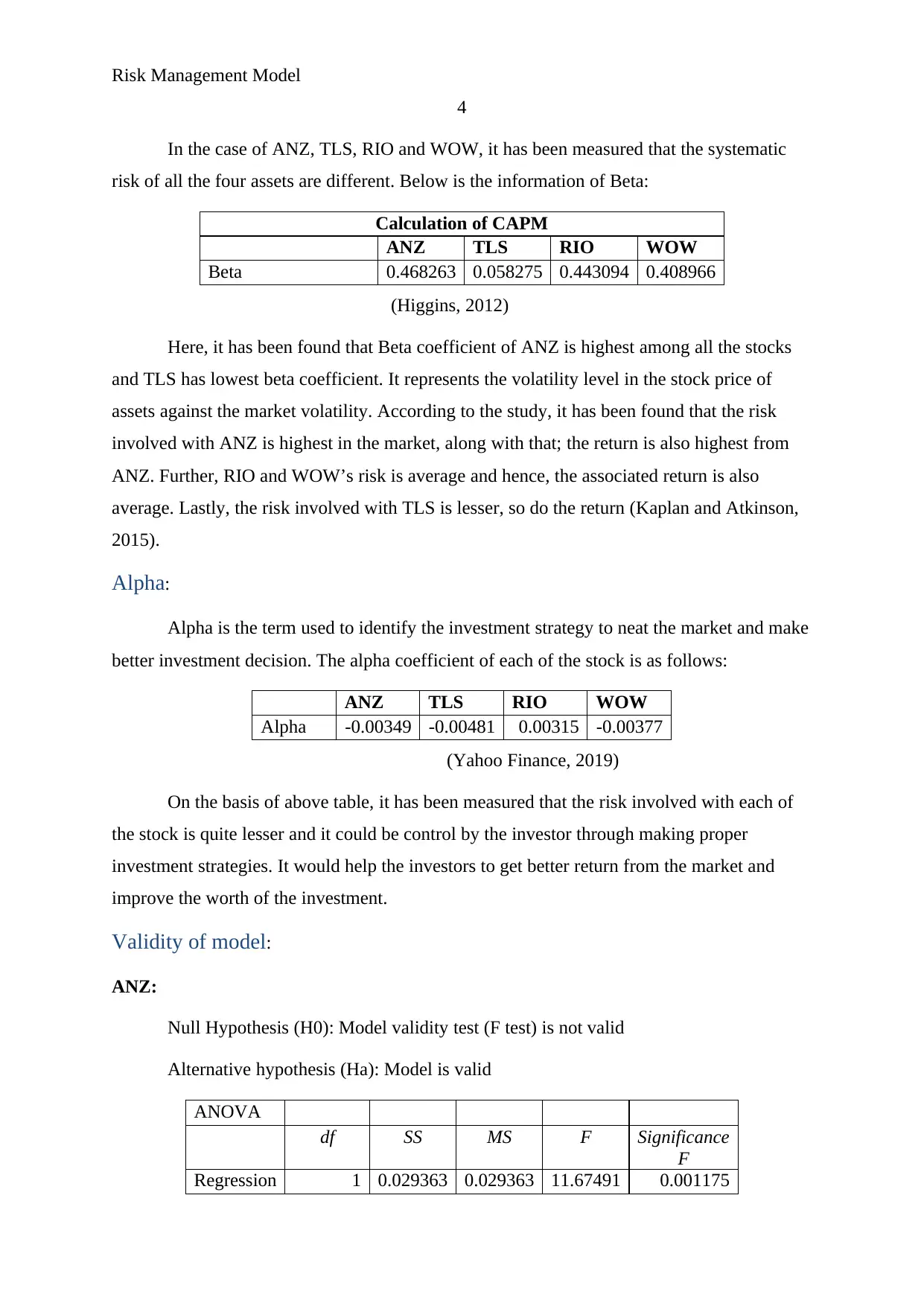
Calculation of CAPM
ANZ TLS RIO WOW
Beta 0.468263 0.058275 0.443094 0.408966
(Higgins, 2012)
Here, it has been found that Beta coefficient of ANZ is highest among all the stocks
and TLS has lowest beta coefficient. It represents the volatility level in the stock price of
assets against the market volatility. According to the study, it has been found that the risk
involved with ANZ is highest in the market, along with that; the return is also highest from
ANZ. Further, RIO and WOW’s risk is average and hence, the associated return is also
average. Lastly, the risk involved with TLS is lesser, so do the return (Kaplan and Atkinson,
2015).
Alpha:
Alpha is the term used to identify the investment strategy to neat the market and make
better investment decision. The alpha coefficient of each of the stock is as follows:
ANZ TLS RIO WOW
Alpha -0.00349 -0.00481 0.00315 -0.00377
(Yahoo Finance, 2019)
On the basis of above table, it has been measured that the risk involved with each of
the stock is quite lesser and it could be control by the investor through making proper
investment strategies. It would help the investors to get better return from the market and
improve the worth of the investment.
Validity of model:
ANZ:
Null Hypothesis (H0): Model validity test (F test) is not valid
Alternative hypothesis (Ha): Model is valid
ANOVA
df SS MS F Significance
F
Regression 1 0.029363 0.029363 11.67491 0.001175
4
In the case of ANZ, TLS, RIO and WOW, it has been measured that the systematic
risk of all the four assets are different. Below is the information of Beta:
Calculation of CAPM
ANZ TLS RIO WOW
Beta 0.468263 0.058275 0.443094 0.408966
(Higgins, 2012)
Here, it has been found that Beta coefficient of ANZ is highest among all the stocks
and TLS has lowest beta coefficient. It represents the volatility level in the stock price of
assets against the market volatility. According to the study, it has been found that the risk
involved with ANZ is highest in the market, along with that; the return is also highest from
ANZ. Further, RIO and WOW’s risk is average and hence, the associated return is also
average. Lastly, the risk involved with TLS is lesser, so do the return (Kaplan and Atkinson,
2015).
Alpha:
Alpha is the term used to identify the investment strategy to neat the market and make
better investment decision. The alpha coefficient of each of the stock is as follows:
ANZ TLS RIO WOW
Alpha -0.00349 -0.00481 0.00315 -0.00377
(Yahoo Finance, 2019)
On the basis of above table, it has been measured that the risk involved with each of
the stock is quite lesser and it could be control by the investor through making proper
investment strategies. It would help the investors to get better return from the market and
improve the worth of the investment.
Validity of model:
ANZ:
Null Hypothesis (H0): Model validity test (F test) is not valid
Alternative hypothesis (Ha): Model is valid
ANOVA
df SS MS F Significance
F
Regression 1 0.029363 0.029363 11.67491 0.001175
Secure Best Marks with AI Grader
Need help grading? Try our AI Grader for instant feedback on your assignments.

Risk Management Model
5
Residual 57 0.143358 0.002515
Total 58 0.172721
Significance Value <0.05
Calculated significance = 0.001175<0.05
It defines that model test is valid (Fulin, 2011)
TLS:
Null Hypothesis (H0): Model validity test (F test) is not valid
Alternative hypothesis (Ha): Model is valid
ANOVA
df SS MS F Significance
F
Regression 1 0.000455 0.000455 0.189423 0.665041
Residual 57 0.136844 0.002401
Total 58 0.137299
Significance Value <0.05
Calculated significance = 0.665041>0.05
It defines that model test is not valid
RIO:
Null Hypothesis (H0): Model validity test (F test) is not valid
Alternative hypothesis (Ha): Model is valid
ANOVA
df SS MS F Significance
F
Regression 1 0.026292 0.026292 6.079539 0.016709
Residual 57 0.246502 0.004325
Total 58 0.272793
Significance Value <0.05
5
Residual 57 0.143358 0.002515
Total 58 0.172721
Significance Value <0.05
Calculated significance = 0.001175<0.05
It defines that model test is valid (Fulin, 2011)
TLS:
Null Hypothesis (H0): Model validity test (F test) is not valid
Alternative hypothesis (Ha): Model is valid
ANOVA
df SS MS F Significance
F
Regression 1 0.000455 0.000455 0.189423 0.665041
Residual 57 0.136844 0.002401
Total 58 0.137299
Significance Value <0.05
Calculated significance = 0.665041>0.05
It defines that model test is not valid
RIO:
Null Hypothesis (H0): Model validity test (F test) is not valid
Alternative hypothesis (Ha): Model is valid
ANOVA
df SS MS F Significance
F
Regression 1 0.026292 0.026292 6.079539 0.016709
Residual 57 0.246502 0.004325
Total 58 0.272793
Significance Value <0.05

Risk Management Model
6
Calculated significance = 0.016709<0.05
It defines that model test is valid
WOW:
Null Hypothesis (H0): Model validity test (F test) is not valid
Alternative hypothesis (Ha): Model is valid
ANOVA
df SS MS F Significance
F
Regression 1 0.022397 0.022397 12.4515 0.000833
Residual 57 0.10253 0.001799
Total 58 0.124927
Significance Value <0.05
Calculated significance = 0.000833<0.05
It defines that model test is valid (Higgins, 2012)
Interpretation of R2:
R square is a statistical measure which is used to identify that how close the data has
been fitted into the regression line. It measures the strength of relationship between the model
and the dependent values.
ANZ TLS RIO WOW
R square 0.170003 0.003312 0.096379 0.179283
In case of ANZ, it has been found that there is 17% variation in the Y data because of
the variation in X data which defines that ASX data is not affecting much to ANZ stock price.
Further, the lowest affect of ASX is on TLS stock prices. RIO and WOW have been affected
average by ASX stock prices (Gapenski, 2008).
Required rate of return:
6
Calculated significance = 0.016709<0.05
It defines that model test is valid
WOW:
Null Hypothesis (H0): Model validity test (F test) is not valid
Alternative hypothesis (Ha): Model is valid
ANOVA
df SS MS F Significance
F
Regression 1 0.022397 0.022397 12.4515 0.000833
Residual 57 0.10253 0.001799
Total 58 0.124927
Significance Value <0.05
Calculated significance = 0.000833<0.05
It defines that model test is valid (Higgins, 2012)
Interpretation of R2:
R square is a statistical measure which is used to identify that how close the data has
been fitted into the regression line. It measures the strength of relationship between the model
and the dependent values.
ANZ TLS RIO WOW
R square 0.170003 0.003312 0.096379 0.179283
In case of ANZ, it has been found that there is 17% variation in the Y data because of
the variation in X data which defines that ASX data is not affecting much to ANZ stock price.
Further, the lowest affect of ASX is on TLS stock prices. RIO and WOW have been affected
average by ASX stock prices (Gapenski, 2008).
Required rate of return:
Risk Management Model
7
Required rate of return of all the 4 stocks are as follows:
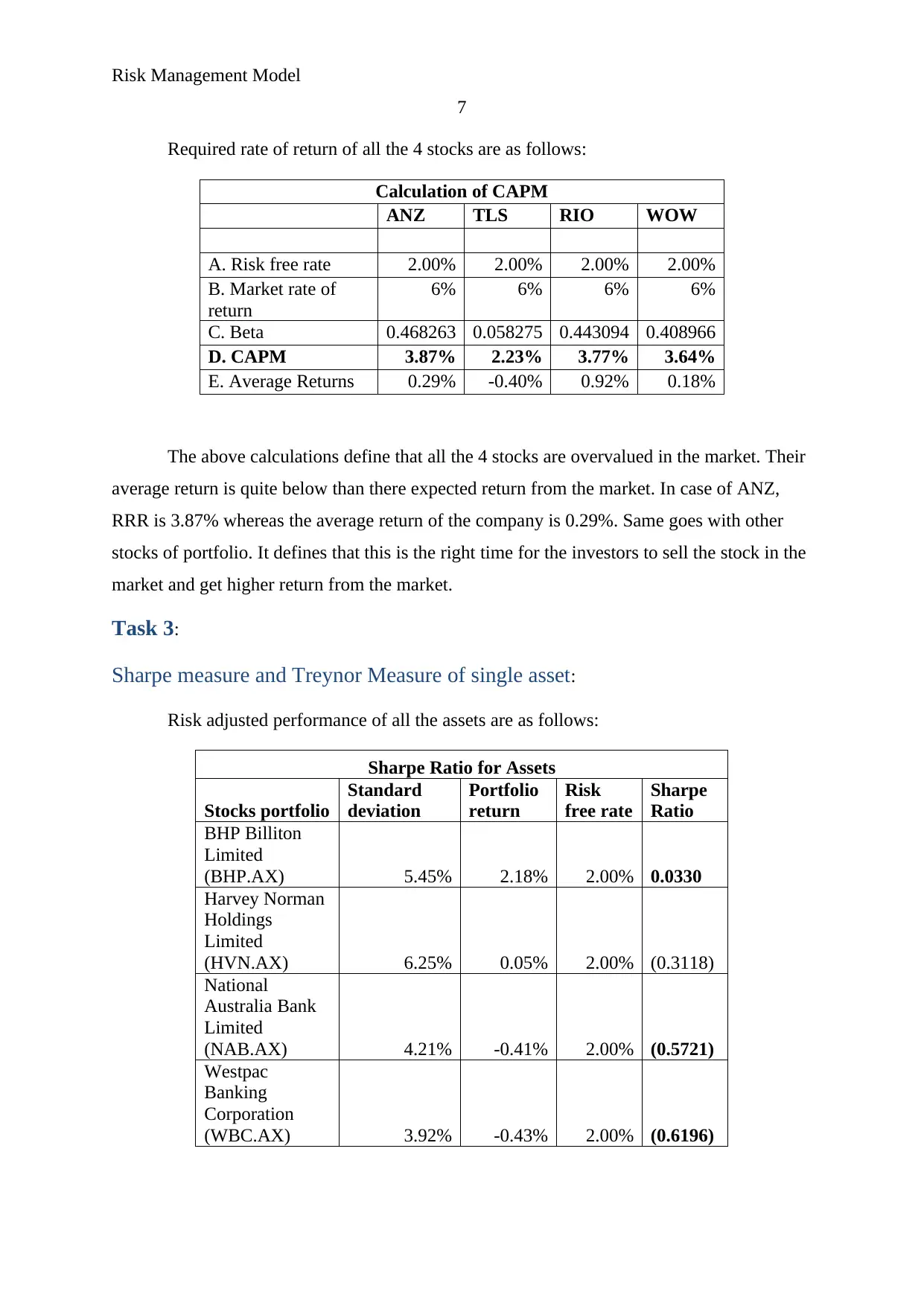
Calculation of CAPM
ANZ TLS RIO WOW
A. Risk free rate 2.00% 2.00% 2.00% 2.00%
B. Market rate of
return
6% 6% 6% 6%
C. Beta 0.468263 0.058275 0.443094 0.408966
D. CAPM 3.87% 2.23% 3.77% 3.64%
E. Average Returns 0.29% -0.40% 0.92% 0.18%
The above calculations define that all the 4 stocks are overvalued in the market. Their
average return is quite below than there expected return from the market. In case of ANZ,
RRR is 3.87% whereas the average return of the company is 0.29%. Same goes with other
stocks of portfolio. It defines that this is the right time for the investors to sell the stock in the
market and get higher return from the market.
Task 3:
Sharpe measure and Treynor Measure of single asset:
Risk adjusted performance of all the assets are as follows:
Sharpe Ratio for Assets
Stocks portfolio
Standard
deviation
Portfolio
return
Risk
free rate
Sharpe
Ratio
BHP Billiton
Limited
(BHP.AX) 5.45% 2.18% 2.00% 0.0330
Harvey Norman
Holdings
Limited
(HVN.AX) 6.25% 0.05% 2.00% (0.3118)
National
Australia Bank
Limited
(NAB.AX) 4.21% -0.41% 2.00% (0.5721)
Westpac
Banking
Corporation
(WBC.AX) 3.92% -0.43% 2.00% (0.6196)
7
Required rate of return of all the 4 stocks are as follows:
Calculation of CAPM
ANZ TLS RIO WOW
A. Risk free rate 2.00% 2.00% 2.00% 2.00%
B. Market rate of
return
6% 6% 6% 6%
C. Beta 0.468263 0.058275 0.443094 0.408966
D. CAPM 3.87% 2.23% 3.77% 3.64%
E. Average Returns 0.29% -0.40% 0.92% 0.18%
The above calculations define that all the 4 stocks are overvalued in the market. Their
average return is quite below than there expected return from the market. In case of ANZ,
RRR is 3.87% whereas the average return of the company is 0.29%. Same goes with other
stocks of portfolio. It defines that this is the right time for the investors to sell the stock in the
market and get higher return from the market.
Task 3:
Sharpe measure and Treynor Measure of single asset:
Risk adjusted performance of all the assets are as follows:
Sharpe Ratio for Assets
Stocks portfolio
Standard
deviation
Portfolio
return
Risk
free rate
Sharpe
Ratio
BHP Billiton
Limited
(BHP.AX) 5.45% 2.18% 2.00% 0.0330
Harvey Norman
Holdings
Limited
(HVN.AX) 6.25% 0.05% 2.00% (0.3118)
National
Australia Bank
Limited
(NAB.AX) 4.21% -0.41% 2.00% (0.5721)
Westpac
Banking
Corporation
(WBC.AX) 3.92% -0.43% 2.00% (0.6196)
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
Risk Management Model
8
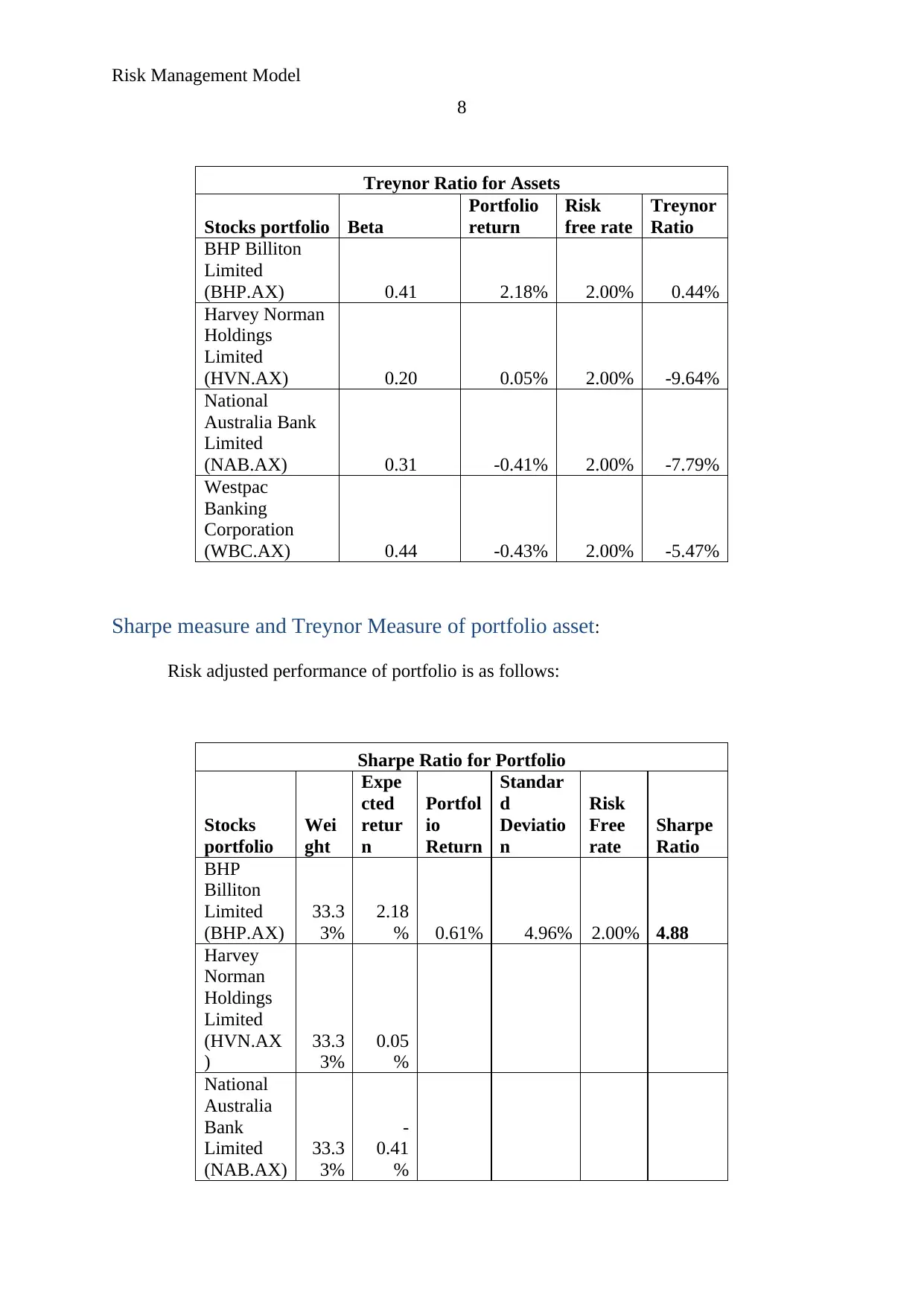
Treynor Ratio for Assets
Stocks portfolio Beta
Portfolio
return
Risk
free rate
Treynor
Ratio
BHP Billiton
Limited
(BHP.AX) 0.41 2.18% 2.00% 0.44%
Harvey Norman
Holdings
Limited
(HVN.AX) 0.20 0.05% 2.00% -9.64%
National
Australia Bank
Limited
(NAB.AX) 0.31 -0.41% 2.00% -7.79%
Westpac
Banking
Corporation
(WBC.AX) 0.44 -0.43% 2.00% -5.47%
Sharpe measure and Treynor Measure of portfolio asset:
Risk adjusted performance of portfolio is as follows:
Sharpe Ratio for Portfolio
Stocks
portfolio
Wei
ght
Expe
cted
retur
n
Portfol
io
Return
Standar
d
Deviatio
n
Risk
Free
rate
Sharpe
Ratio
BHP
Billiton
Limited
(BHP.AX)
33.3
3%
2.18
% 0.61% 4.96% 2.00% 4.88
Harvey
Norman
Holdings
Limited
(HVN.AX
)
33.3
3%
0.05
%
National
Australia
Bank
Limited
(NAB.AX)
33.3
3%
-
0.41
%
8
Treynor Ratio for Assets
Stocks portfolio Beta
Portfolio
return
Risk
free rate
Treynor
Ratio
BHP Billiton
Limited
(BHP.AX) 0.41 2.18% 2.00% 0.44%
Harvey Norman
Holdings
Limited
(HVN.AX) 0.20 0.05% 2.00% -9.64%
National
Australia Bank
Limited
(NAB.AX) 0.31 -0.41% 2.00% -7.79%
Westpac
Banking
Corporation
(WBC.AX) 0.44 -0.43% 2.00% -5.47%
Sharpe measure and Treynor Measure of portfolio asset:
Risk adjusted performance of portfolio is as follows:
Sharpe Ratio for Portfolio
Stocks
portfolio
Wei
ght
Expe
cted
retur
n
Portfol
io
Return
Standar
d
Deviatio
n
Risk
Free
rate
Sharpe
Ratio
BHP
Billiton
Limited
(BHP.AX)
33.3
3%
2.18
% 0.61% 4.96% 2.00% 4.88
Harvey
Norman
Holdings
Limited
(HVN.AX
)
33.3
3%
0.05
%
National
Australia
Bank
Limited
(NAB.AX)
33.3
3%
-
0.41
%
Risk Management Model
9
Treynor Ratio for Portfolio
Stocks
portfolio
Wei
ght
Expe
cted
retur
n
Portfol
io
Return
Standar
d
Deviatio
n
Risk
Free
rate
Treyno
r Ratio
BHP
Billiton
Limited
(BHP.AX)
33.3
3%
2.18
% 0.61% 3.40% 2.00% 2.31
Harvey
Norman
Holdings
Limited
(HVN.AX
)
33.3
3%
0.05
%
National
Australia
Bank
Limited
(NAB.AX)
33.3
3%
-
0.41
%
Comparison among the results:
Sharpe ration defines about the performance of an investment. It compares the
investment risk with risk free assets after adjusting all the risk. Further treynor ratio defines
about the investment performance of a security on the basis of systematic risk.
On the basis of above results, it has been found that the Sharpe ratio of individual
assets is lower than the portfolio Sharpe ratio. Further, Treynor ratio of individual assets is
lower than the portfolio Treynor ratio (Elton, Gruber, Brown and Goetzmann, 2009). It
defines that it is better option for the investors to make investment in portfolio instead of an
individual asset.
9
Treynor Ratio for Portfolio
Stocks
portfolio
Wei
ght
Expe
cted
retur
n
Portfol
io
Return
Standar
d
Deviatio
n
Risk
Free
rate
Treyno
r Ratio
BHP
Billiton
Limited
(BHP.AX)
33.3
3%
2.18
% 0.61% 3.40% 2.00% 2.31
Harvey
Norman
Holdings
Limited
(HVN.AX
)
33.3
3%
0.05
%
National
Australia
Bank
Limited
(NAB.AX)
33.3
3%
-
0.41
%
Comparison among the results:
Sharpe ration defines about the performance of an investment. It compares the
investment risk with risk free assets after adjusting all the risk. Further treynor ratio defines
about the investment performance of a security on the basis of systematic risk.
On the basis of above results, it has been found that the Sharpe ratio of individual
assets is lower than the portfolio Sharpe ratio. Further, Treynor ratio of individual assets is
lower than the portfolio Treynor ratio (Elton, Gruber, Brown and Goetzmann, 2009). It
defines that it is better option for the investors to make investment in portfolio instead of an
individual asset.

Risk Management Model
10
References:
Elton, E.J., Gruber, M.J., Brown, S.J., and Goetzmann, W.N. 2009. Modern Portfolio Theory
and Investment Analysis. John Wiley and Sons, United Kingdom.
Fulin, S. 2011. Preface by SHANG Fulin. Corporate Governance of Listed Companies in
China. OECD, 5, p.003.
Gapenski, L.C., 2008. Healthcare finance: an introduction to accounting and financial
management. Health Administration Press.
Higgins, R. C., 2012. Analysis for financial management. McGraw-Hill/Irwin.
Kaplan, R.S. and Atkinson, A.A., 2015. Advanced management accounting. PHI Learning.
Moles, P. Parrino, R and Kidwekk, D,.2011. Corporate finance, European edition, John
Wiley andsons, United Kingdom.
10
References:
Elton, E.J., Gruber, M.J., Brown, S.J., and Goetzmann, W.N. 2009. Modern Portfolio Theory
and Investment Analysis. John Wiley and Sons, United Kingdom.
Fulin, S. 2011. Preface by SHANG Fulin. Corporate Governance of Listed Companies in
China. OECD, 5, p.003.
Gapenski, L.C., 2008. Healthcare finance: an introduction to accounting and financial
management. Health Administration Press.
Higgins, R. C., 2012. Analysis for financial management. McGraw-Hill/Irwin.
Kaplan, R.S. and Atkinson, A.A., 2015. Advanced management accounting. PHI Learning.
Moles, P. Parrino, R and Kidwekk, D,.2011. Corporate finance, European edition, John
Wiley andsons, United Kingdom.
Secure Best Marks with AI Grader
Need help grading? Try our AI Grader for instant feedback on your assignments.
Risk Management Model
11
Appendix:
ANZ:
TLS:
RIO:
11
Appendix:
ANZ:
TLS:
RIO:
Risk Management Model
12
WOW:
12
WOW:
1 out of 12
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
© 2024 | Zucol Services PVT LTD | All rights reserved.

