Average Value of a Function over a Region

Learn how to calculate the average value of a function over a given region using integration techniques. Understand the concept of average value and its application in various scenarios. Get step-by-step solutions and examples.

Proof
Let f (x, y) be a continuous realvalued function D be a closed,connected
region, that has area A(D).
We first state the Extreme Value Theorem for function in two variables:
According to B,Hass,Heil and Weir (2018),“Let f (x, y) be a continuous
function.If D is a closed and bounded region then there exists (x1, y1),(x2, y2)
∈ D such that f (x1, y1) is an absolute maximum of f and f (x2, y2) is an ab-
solute minimum of f .”
Thus, by Extreme Value Theorem
f (x1, y1) ≤ f (x, y) ≤ f (x2, y2) (1)
Integrating (1) over D
ZZ
D
f (x1, y1) dA ≤
ZZ
D
f (x, y) dA ≤
ZZ
D
f (x2, y2) dA
[
ZZ
D
dA = A(D)]
∴ A(D)f(x 1, y1) ≤
ZZ
D
f (x, y) dA ≤ A(D)f (x2, y2)
[Divide throughout by A(D)]
1

f (x1, y1) ≤ 1
A(D)
ZZ
D
f (x, y) dA ≤ f (x2, y2)
According to B,Hass,Heil and Weir (2018),“By Intermediate Value The-
orem,a continuous function f (x, y) on D,takes every value between it’s
maximum and minimum,therefore,there must a point (x0, y0) ∈ D, such
that”
f (x0, y0) = 1
A(D)
ZZ
D
f (x, y) dA
Multiplying throughout by A(D)
ZZ
D
f (x, y) dA = f (x0, y0) A(D)
which is the Mean Value Theorem in two variables.Hence proved.
Answer
A disk D centered at origin with radius a is shown in figure-1 below.
Figure 1:Disk at origin with radius=a
2

Consider any point P (x, y) which lies inside D.Its distance from the origin
O is given by
d(x, y) =
p x2 + y2
Average value of a function f (x, y) over a bounded region R in the xy- plane
is calculated using formula
f ave = 1
A(R)
ZZ
R
f (x, y) dA (1)
where, A(R) is the area of R.
Area of disk D is:A(D) = πr2 = πa2.
Therefore, by (1), average distance of points in D from origin O is
dave = 1
A(D)
ZZ
D
d(x, y) dA
= 1
π a2
ZZ
D
p x2 + y2 dA
For convenience, switch to polar coordinates (r, θ).
x = r cos θ,y = r sin θ
Area element of a disk is given by:dA = rdrdθ.
In the region D, r varies from 0 to a while θ varies from 0 to 2π.Therefore,
dave = 1
π a2
ZZ
D
√ r2 rdrdθ
[Applying limits to the integral]
= 1
π a2
Z 2π
0
Z a
0
r2 drdθ
= 1
π a2
Z 2π
0
r3
3
a
0
dθ
3

= 1
π a2
Z 2π
0
a3
3 dθ
= a
3π
Z 2π
0
dθ
= a
3π 2π
∴ dave = 2a
3
Thus, the average value of distance of points from origin, in a disk centered
at origin with radius a is
2a
3 .
4

Answer
a)
5

ZZ
R2
f (x, y) dA = lim
a→∞
ZZ
aD
f (x, y) dA
where, aD is a disk centered at origin with radius = a.
Let,
f (x, y) = e−(x2+y2)
Implies,
ZZ
R2
e−(x2+y2) dA = lim
a→∞
ZZ
aD
e−(x2+y2) dA (1)
In order to evaluate the right side of (1), we switch to polar coordinates
(r, θ) in aD and then take the limit of the evaluated integral.
x = r cos θ,y = r sin θ [0 ≤ r ≤ a,0 ≤ θ ≤ 2π]
Area element of the disk is given by:dA = rdrdθ.Therefore,
ZZ
aD
e−(x2+y2) dA =
ZZ
D
e−r 2
· rdrdθ
[Applying Limits]
=
Z 2π
0
Z a
0
re−r2
drdθ
[Substitute:− r2 = t]
=
Z 2π
0
dθ
Z a
0
−1
2et dt
= −1
2
Z 2π
0
dθ
h
e−r2 i a
0
6

= −1
2(e−a2
− 1)
Z 2π
0
dθ
∴
ZZ
aD
e−(x2+y2) dA = −π(e−a2
− 1)
Taking the limit to evaluate the improper integral
ZZ
R2
e−(x2+y2) dA = lim
a→∞ −π(e−a2
− 1)
= lim
a→∞ π − lim
a→∞ πe−a2
= π − 0
∴
ZZ
R2
e−(x2+y2) dA = π
b)
An equivalent definition is given by
ZZ
R2
e−(x2+y2) dA = lim
a→∞
ZZ
aS
e−(x2+y2) dA (2)
where, aS is a square with vertices (±a, ±a).
Within aS,x varies from −a to +a and y also varies from −a to +a.Area
element of square is given by:dA = dxdy.Therefore, applying limits
lim
a→∞
ZZ
aS
e−(x2+y2) dA = lim
a→∞
Z +a
−a
Z +a
−a
e−x2
e−y2
dxdy
[Integral in (2) is equal to π]
[Using Fubini’s Theorem Corollary (B, Hass, Heil and Weir, 2018)]
7

∴ π = lim
a→∞
Z +a
−a
e−x2
dx
Z +a
−a
e−y2
dy
[Taking limit to each integral]
π = lim
a→∞
Z +a
−a
e−x2
dx lim
a→∞
Z +a
−a
e−y2
dy
[As both terms on the right together converge to π,
limit of each term exists and is finite ]
[Applying limit to each integral]
π =
Z +∞
−∞
e−x2
dx
Z +∞
−∞
e−y2
dy
c)
From (b) we have
Z +∞
−∞
e−x2
dx
Z +∞
−∞
e−y2
dy = π (3)
The two integrals on the left in (3) are the same except being expressed in
different variables.Therefore they must be equal.
This implies,
Z +∞
−∞
e−x2
dx
Z +∞
−∞
e−y2
dy =
Z +∞
−∞
e−x2
dx
Z +∞
−∞
e−x2
dx
8

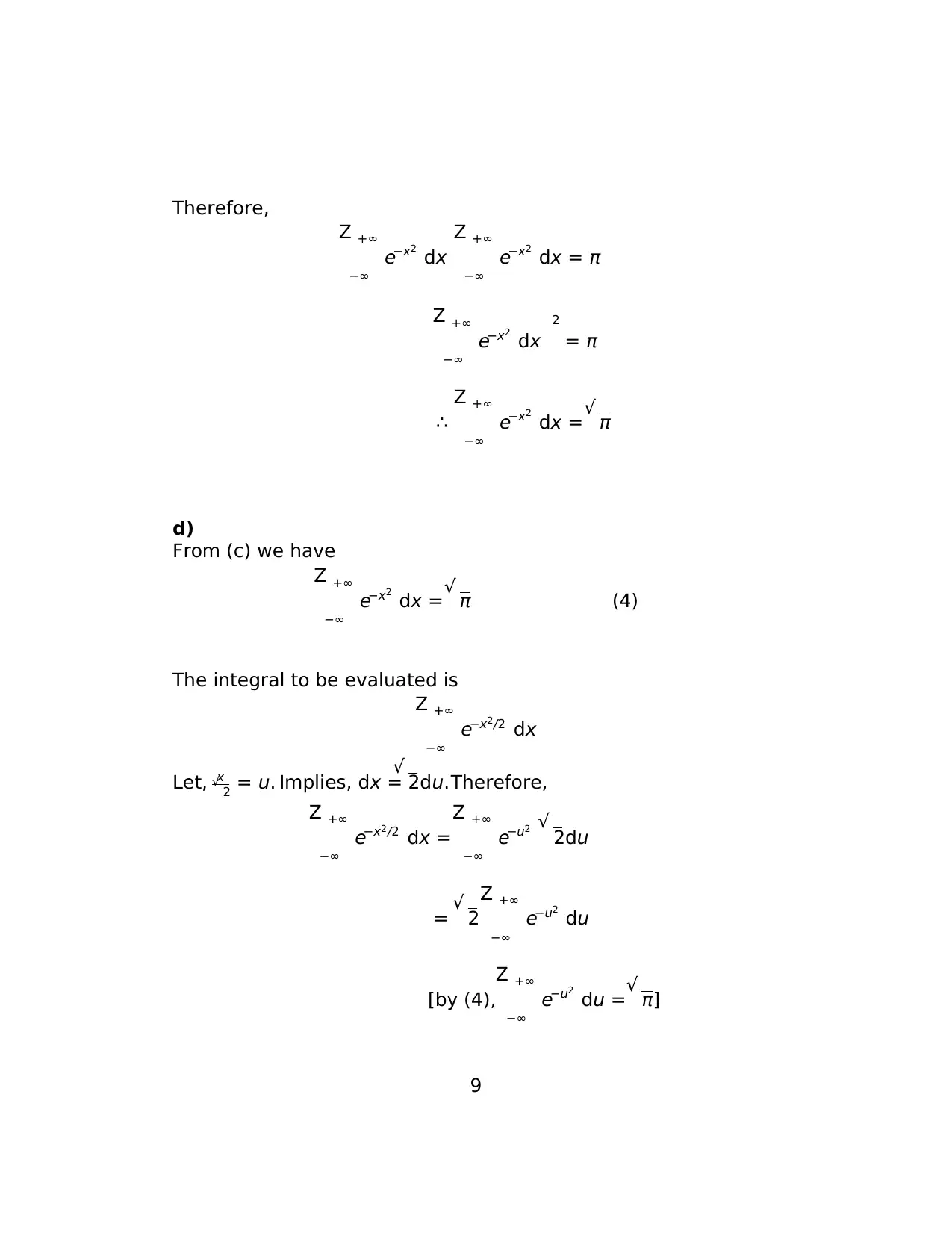
Therefore,
Z +∞
−∞
e−x2
dx
Z +∞
−∞
e−x2
dx = π
Z +∞
−∞
e−x2
dx
2
= π
∴
Z +∞
−∞
e−x2
dx =√ π
d)
From (c) we have
Z +∞
−∞
e−x2
dx =√ π (4)
The integral to be evaluated is
Z +∞
−∞
e−x2/2 dx
Let, x√ 2 = u. Implies, dx =
√ 2du.Therefore,
Z +∞
−∞
e−x2/2 dx =
Z +∞
−∞
e−u2 √ 2du
= √ 2
Z +∞
−∞
e−u2
du
[by (4),
Z +∞
−∞
e−u2
du =√ π]
9

∴
Z +∞
−∞
e−x2/2 dx =√ 2π
Answer
There are two main advantages to the function notation f :D → R com-
pared to the textbook notation f (x, y, z):
1. f : D → R, packs the information about domain of the function which
cannot be conveyed in the other notation.Functions, at times, have meaning
only within a certain set of inputs (domain).Like in this notation it is clearly
indicated that f is defined over the domain D.
2. f : D → R, also indicates the set to which the function maps the inputs.
Like for the given notation it is understood that f maps D to a set of real
numbers R.A function g may map D to a set ofcomplex numbers which
then is denoted as g :D → C. The textbook notation does not carry this
information.
10

Answer
a)
E is a cube with side length equal to L.Therefore, its volume
V (E) = L3
One ofthe vertex ofthe cube lies at the origin and the edges ofcube are
all in the first quadrant,parallelto the coordinate axes.This construction
describes a cube occupying region with limits:0 ≤ x ≤ L, 0 ≤ y ≤ L, 0 ≤
z ≤ L.
Given function is
f (x, y, z) = xyz
Average value of f over E is given by the formula
f ave = 1
V (E)
ZZZ
E
f (x, y, z) dV
Therefore,
f ave = 1
L 3
ZZZ
E
xyz dV
[Applying limits]
= 1
L 3
Z L
0
Z L
0
Z L
0
xyz dxdydz
= 1
L 3
Z L
0
x dx
Z L
0
y dy
Z L
0
z dz
[but,
Z L
0
x dx =
Z L
0
y dy =
Z L
0
z dz]
∴ = 1
L 3
Z L
0
x dx
3
11

= 1
L 3
x2
2
L
0
! 3
∴ f ave = 1
L 3 · L 6
8 = L 3
8
b)
Height of points in a solid hemisphere is given by the function
f (x, y, z) = z
Average height of points over the hemisphere is obtained using the formula
f ave = 1
V (E)
ZZZ
E
f (x, y, z) dV
E is a hemisphere defined as:x2 + y2 + z2 ≤ 1 z ≥ 0, which implies E is
centered at origin with radius = 1 and lies above the plane z = 0.
Volume of E is calculated as
V (E) = 1
2 × 4
3π r3 = 2π
3
Average height is therefore obtained as
f ave = 3
2π
ZZZ
E
z dV
For convenience, switch to spherical coordinates r, θ, φ over E:
x = r cos θ sin φ,y = r sin θ sin φ,z = r cos φ
Within E, r, θ and φ vary as:0 ≤ r ≤ 1, 0 ≤ θ ≤ 2π and 0 ≤ φ ≤ π/2.
Elemental volume of a sphere is:dV = r2 sin φ dφdrdθ.
12

Therefore,
f ave = 3
2π
ZZZ
E
r cos φ · r2 sin φ dφdrdθ
[Trig. Identity:cos x sin x =
sin 2x
2 ]
= 3
2π
ZZZ
E
r3
2 sin (2φ) dφdrdθ
[Applying Limits]
= 3
4π
Z 2π
0
Z 1
0
Z π/2
0
r3 sin (2π) dφdrdθ
= 3
4π
Z 2π
0
Z 1
0
r3 −cos (2φ)
2
π/2
0
drdθ
= 3
4π
Z 2π
0
Z 1
0
r3 drdθ
= 3
4π
Z 2π
0
r4
4
1
0
dθ
= 3
16π
Z 2π
0
dθ = 3
16π× 2π =3
8
Thus the average height of all the points in the hemisphere E is
3
8.
13

References:
B, G., Hass, J., Heil, C. R.,Weir, M. D. (2018).Thomas’ Calculus:Multi-
variable.Boston:Pearson.
Zill, D. G., Wright,W. S. (2011).Multivariable Calculus.Sudbury,Mass:
Jones and Bartlett Publishers.
14