Preliminary Results of Psychology Experiment Research Proposal

The preliminary results section of a psychology experiment research proposal includes a linear regression analysis of mean size judgment given to each of the seven body categories. It also discusses serial dependencies in body size estimation and correlation between the magnitude of serial dependence and precision thresholds of individual subjects. The chart titles and references are also provided.

PRELIMINARY RESULTS For Group Research proposal ( Genevieve )
Previous studies support the efficiency of the proposed statistical
method to measure perception of body sizes allocated to different
categories.
Using a Linear regression analysis, we will plot the mean size
judgment given to each of the seven body categories, on linear
axes. The Alexi Et al., 2018 study data showed that mean body size
judgments increase monotonically, and almost linearly with
physical body size (R2 = 0.99 for linear fit). This suggests that the
size categories were perceived as equidistant. We expect our
estimated slope to approximate that found by Cornelissen and
colleagues (Cornelissen, et. al., 2016) which was (0.72)..
Following the conventions of Cicchini, et al. 2012
we will define a regression index as the difference from unit slope,
an index ranging from zero to 1 (where 1 = total regression to the
mean).

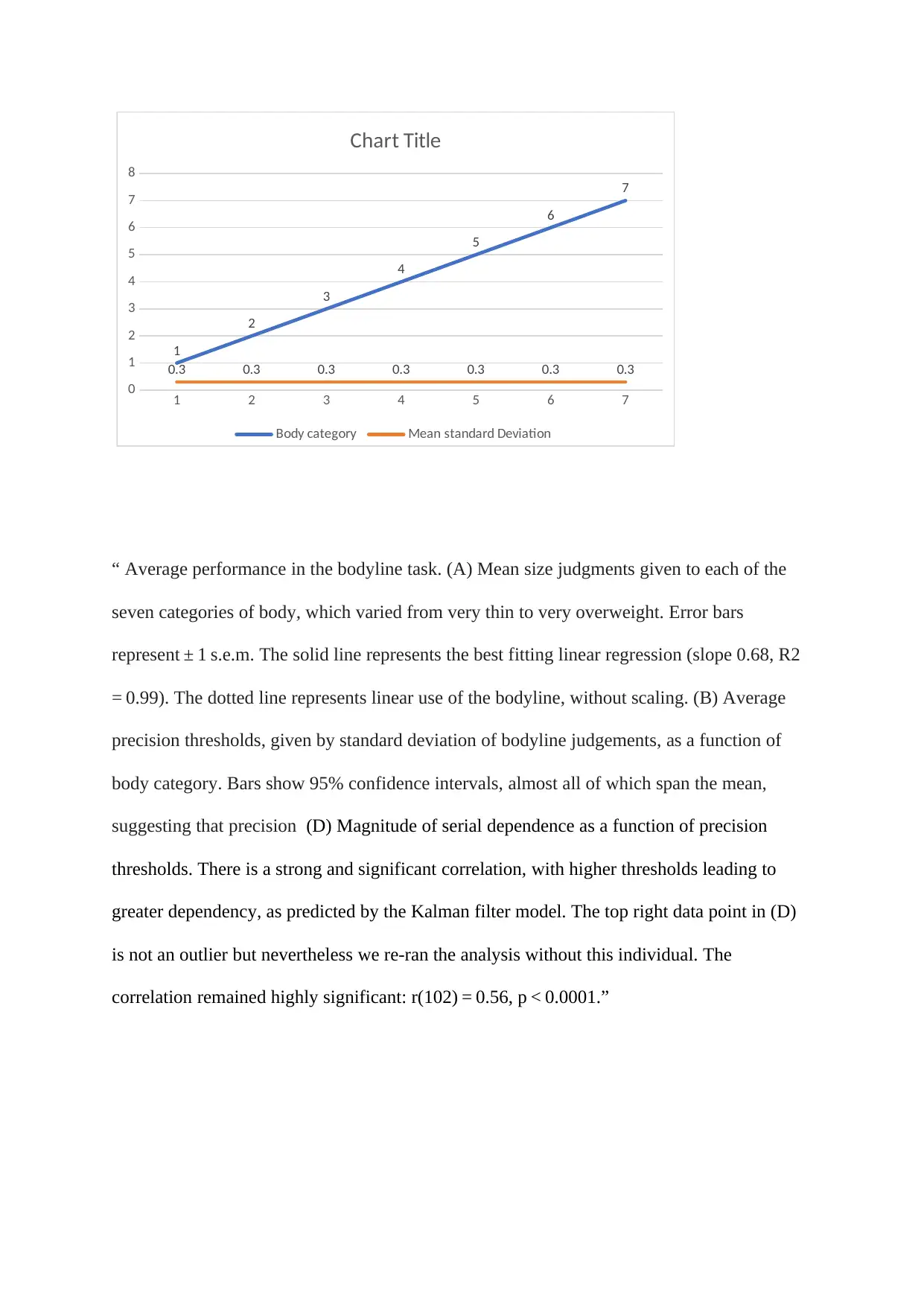
1 2 3 4 5 6 7
0
1
2
3
4
5
6
7
8
1
2
3
4
5
6
7
0.3 0.3 0.3 0.3 0.3 0.3 0.3
Chart Title
Body category Mean standard Deviation
“ Average performance in the bodyline task. (A) Mean size judgments given to each of the
seven categories of body, which varied from very thin to very overweight. Error bars
represent ± 1 s.e.m. The solid line represents the best fitting linear regression (slope 0.68, R2
= 0.99). The dotted line represents linear use of the bodyline, without scaling. (B) Average
precision thresholds, given by standard deviation of bodyline judgements, as a function of
body category. Bars show 95% confidence intervals, almost all of which span the mean,
suggesting that precision (D) Magnitude of serial dependence as a function of precision
thresholds. There is a strong and significant correlation, with higher thresholds leading to
greater dependency, as predicted by the Kalman filter model. The top right data point in (D)
is not an outlier but nevertheless we re-ran the analysis without this individual. The
correlation remained highly significant: r(102) = 0.56, p < 0.0001.”

1 2 3 4 5 6 7
-4
-3
-2
-1
0
1
2
3
4
5
6
Chart Title
Serial dependencies in body size estimation. Data show the average
biases in the perceived size (difference between perceived and
physical size), as a function of the difference in size of the body on
the preceding trial. Data are averaged over all observers and body
categories. Error bars represent ± 1 s.e.m. The continuous curve
shows the predictions of the parameter-free Kalman filter model .
The horizontal dotted line plots the average bias, which is slightly
negative.
Serial Dependence in Perceived Body Size
To test for serial dependence, i.e., influence from images in the
preceding trial, Data in the Alexi et al., 2018 study showed that
body size judgments are systematically biased towards prior
experience: bodies were perceived as smaller when preceded by a
smaller body (lower left quadrant) and perceived as larger when
preceded by a larger body (upper right quadrant).

The assimilative bias increased with the difference in size of past
and present images, up to a maximum effect for a difference of two
body size units, and then reduced in magnitude for larger size
differences. This selectivity indicates a highly sophisticated system
that assimilates across small but not large size differences.
We will test for a correlation between the magnitude of
serial dependence and precision thresholds of individual subjects.
Central Tendency - Regression to the mean has recently been
formulated in Bayesian terms, in which the mean can be considered
a priori “best guess” before any measurement is made. The prior is
statistically combined with the sensory information, termed the
likelihood, to yield the most efficient estimate of the judgment
(termed the posterior). They show that although it leads to
systematic biases towards the mean, this strategy can reduce the
overall error (which is a combination of bias and precision) by
increasing the precision.
1. Serial Dependencies
Serial dependencies will be modelled using the Kalman filter
model of Cicchini, et al. which assumes that the response R i
to the current stimulus X i is given by a weighted sum of the
current and previous stimuli:We will also calculate the overall
Magnitude of serial dependence:

REFERENCES
Alexi, J., Cleary, D., Dommisse, K. et al. Past visual experiences
weigh in on body size estimation. Sci Rep 8, 215 (2018).
https://doi.org/10.1038/s41598-017-18418-3
CAS Article Google Scholar
Cornelissen, K. K., Gledhill, L. J., Cornelissen, P. L. & Tovée, M. J.
Visual biases in judging body weight. British Journal of Health
Psychology 21, 555–569, https://doi.org/10.1111/bjhp.12185 (2016).
CAS Article Google Scholar
Cicchini, G. M. et al. Optimal encoding of interval timing in expert
percussionists. The Journal of neuroscience: the official journal of
the Society for Neuroscience 32, 1056,
https://doi.org/10.1523/JNEUROSCI.3411-11.2012 (2012).
CAS Article Google Scholar