Assignment 1: Public Key Cryptography and RSA Algorithm (BIT 112)

This assignment delves into the concept of public key cryptography, specifically focusing on the RSA algorithm. The solution begins with an introduction to public and private keys, highlighting their roles in encryption and decryption, and contrasts this with symmetric key algorithms. The assignment then guides the reader through the process of generating public and private keys using the RSA algorithm, demonstrating the process with example prime numbers. The core of the assignment involves using a student ID to generate prime numbers, encrypt the ID with a public key, and then decrypt it using the corresponding private key. The solution leverages the WolframAlpha online software for prime number calculations and demonstrates the encryption and decryption processes. The solution demonstrates the process of key generation, encryption, and decryption, providing a comprehensive understanding of public key cryptography and its practical application.

Running head: PUBLIC KEY CRYPTOGRAPHY
PUBLIC KEY CRYPTOGRAPHY
Name of the Student
Name of the University
Author Note

1PUBLIC KEY CRYPTOGRAPHY
Introduction:
In this assignment the objective is understand the process of public key cryptography and
then to generate private and public key using a certain algorithm from the given Student ID.
The ideas of public and private keys and their relationship are presented in this assignment.
Furthermore, as an example private and public keys are generated by prime number
calculation method using Wolframalpha online software. The concepts of cryptography are
presented by answering the questions in part 1 and part 2.
1. i) Public key cryptography alternatively known as asymmetric cryptography is a particular
encryption scheme that basically uses two related but not same keys known as public key and
private key. This is different from the symmetric key algorithm where the same key is used
for encryption and decryption. In public key cryptography the public key is used for
encryption and private key is used for decryption.
A private key is an extremely large number generated by using some algorithm like wallet
program or any other algorithm. The private key is not shared and only kept to the generator
itself. The public key is generated from the private key and shared to all other persons in the
network. The public key is basically the (x,y) co-ordinates in the elliptical curve after
multiplication of private key number of times. At first a publicly known point is assumed as
initial point G in the curve and then the co-ordinate of the point G is multiplied with the co-
ordinate itself by private key number of time. This reflects the point G on the elliptical curve
by x axis and this process continues until multiplication count reaches private key number of
times. This process is known as pin-ball effect. Hence, after completion of the pin-ball effect
the public key is generated.

2PUBLIC KEY CRYPTOGRAPHY
ii) Now, the RSA algorithm is used here for generation of public and private key. Here, we
have assumed that p and q number are small for ease of calculation but practically p and q are
very large prime numbers.
Let, p = 7 and q = 13.
Hence, pq = 91.
Now, a number e =5 is chosen as e is co-prime to (p-1)(q-1) = 6*12 = 72
Hence, the public key is formed by the pair of numbers (n, e) = (91, 5) an this is made
available to anyone in the network.
Now, inputting the values of p,q and e in the extended Euclidean algorithm outputs the
number d = 29.
Hence, the private key obtained from public key and the extended Euclidean algorithm is (91,
29).
iii) Now, the given student ID is 1464130.
As the bit length of the number is 7 so the number of bits that the number can be represented
with is 7.
iv) Let in the student ID the a particular number of binary bits is 30.
Hence, the number of prime numbers available in that range is found using Wolframalpha as
given below.

3PUBLIC KEY CRYPTOGRAPHY
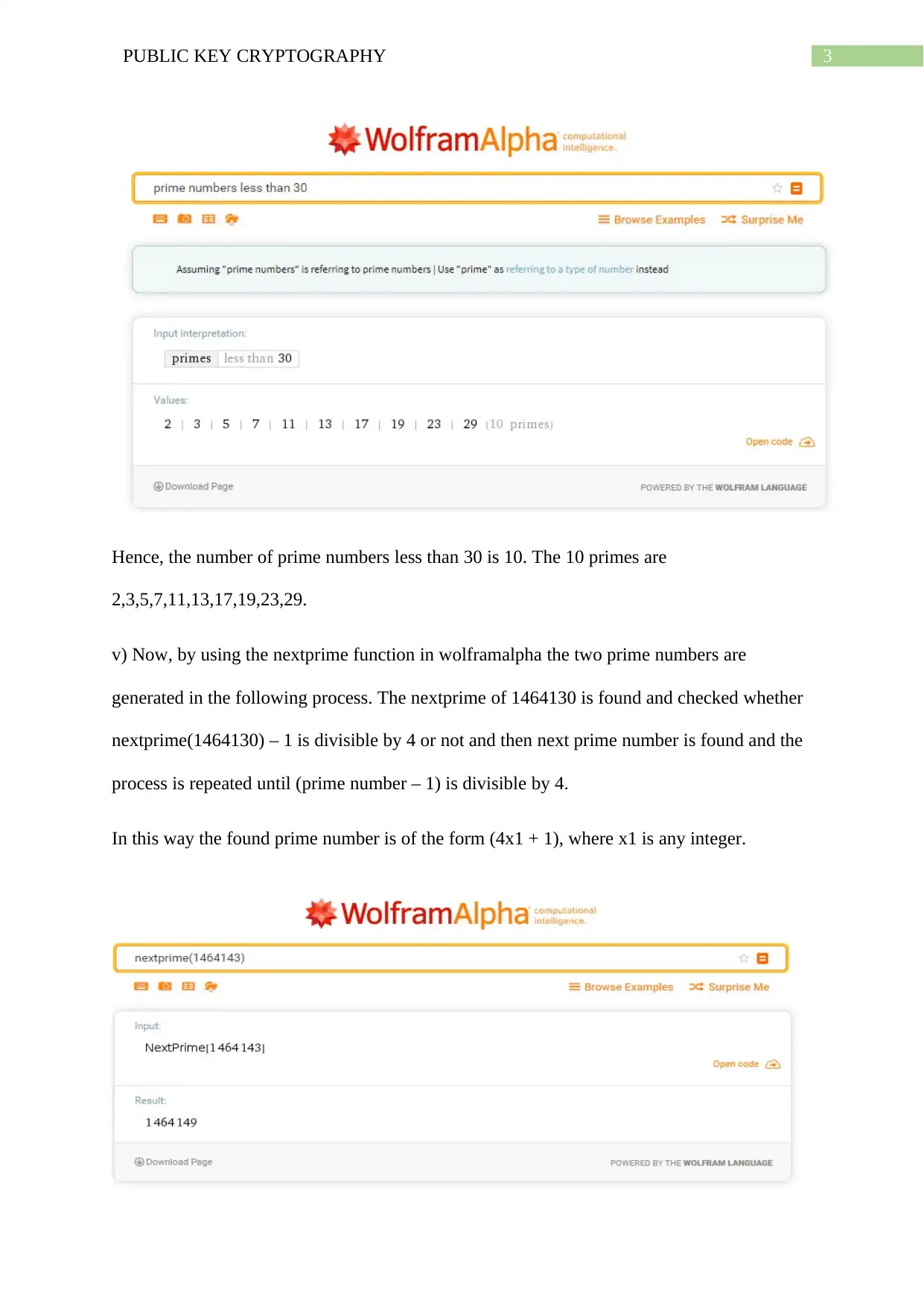
Hence, the number of prime numbers less than 30 is 10. The 10 primes are
2,3,5,7,11,13,17,19,23,29.
v) Now, by using the nextprime function in wolframalpha the two prime numbers are
generated in the following process. The nextprime of 1464130 is found and checked whether
nextprime(1464130) – 1 is divisible by 4 or not and then next prime number is found and the
process is repeated until (prime number – 1) is divisible by 4.
In this way the found prime number is of the form (4x1 + 1), where x1 is any integer.

4PUBLIC KEY CRYPTOGRAPHY
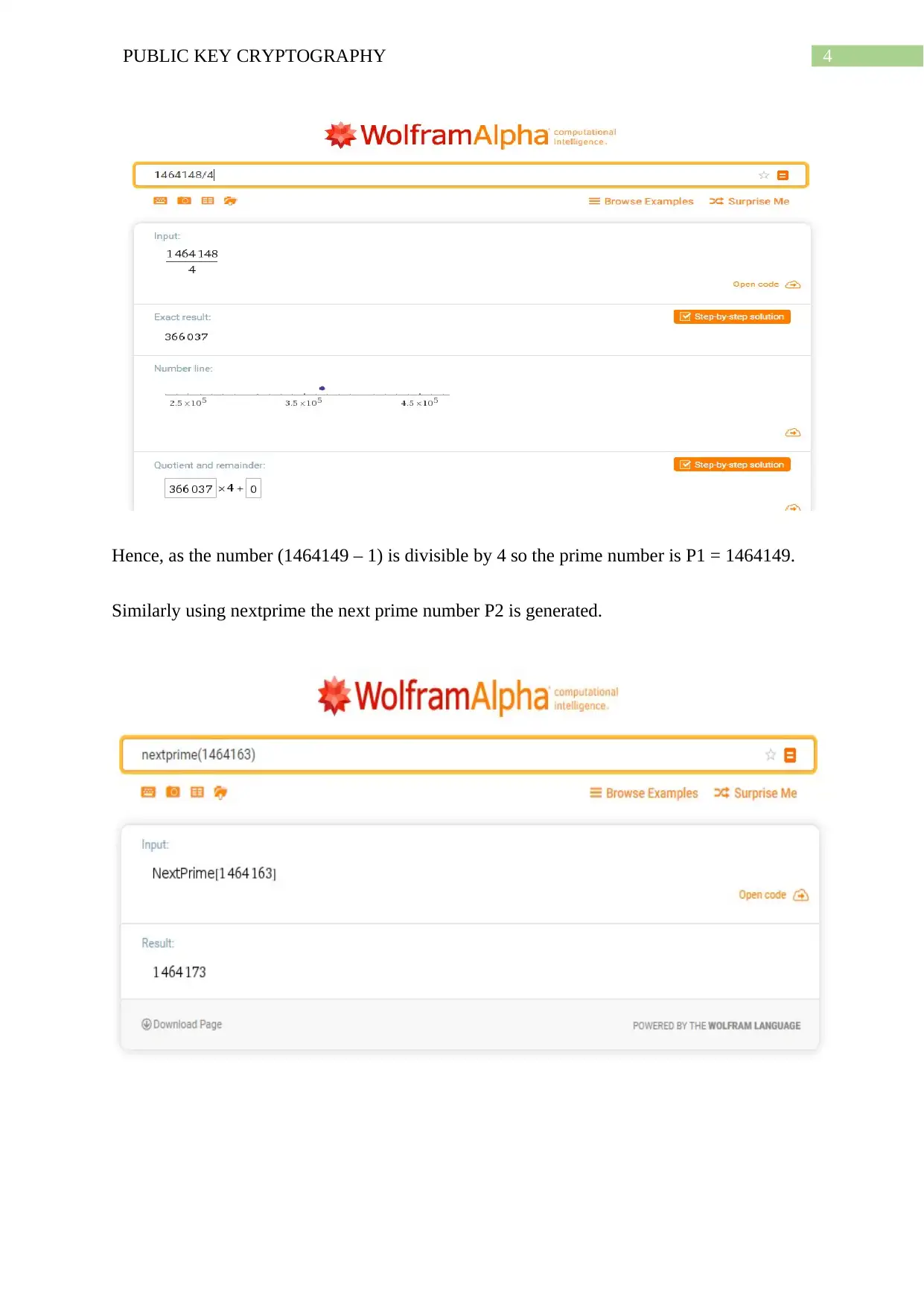
Hence, as the number (1464149 – 1) is divisible by 4 so the prime number is P1 = 1464149.
Similarly using nextprime the next prime number P2 is generated.

5PUBLIC KEY CRYPTOGRAPHY
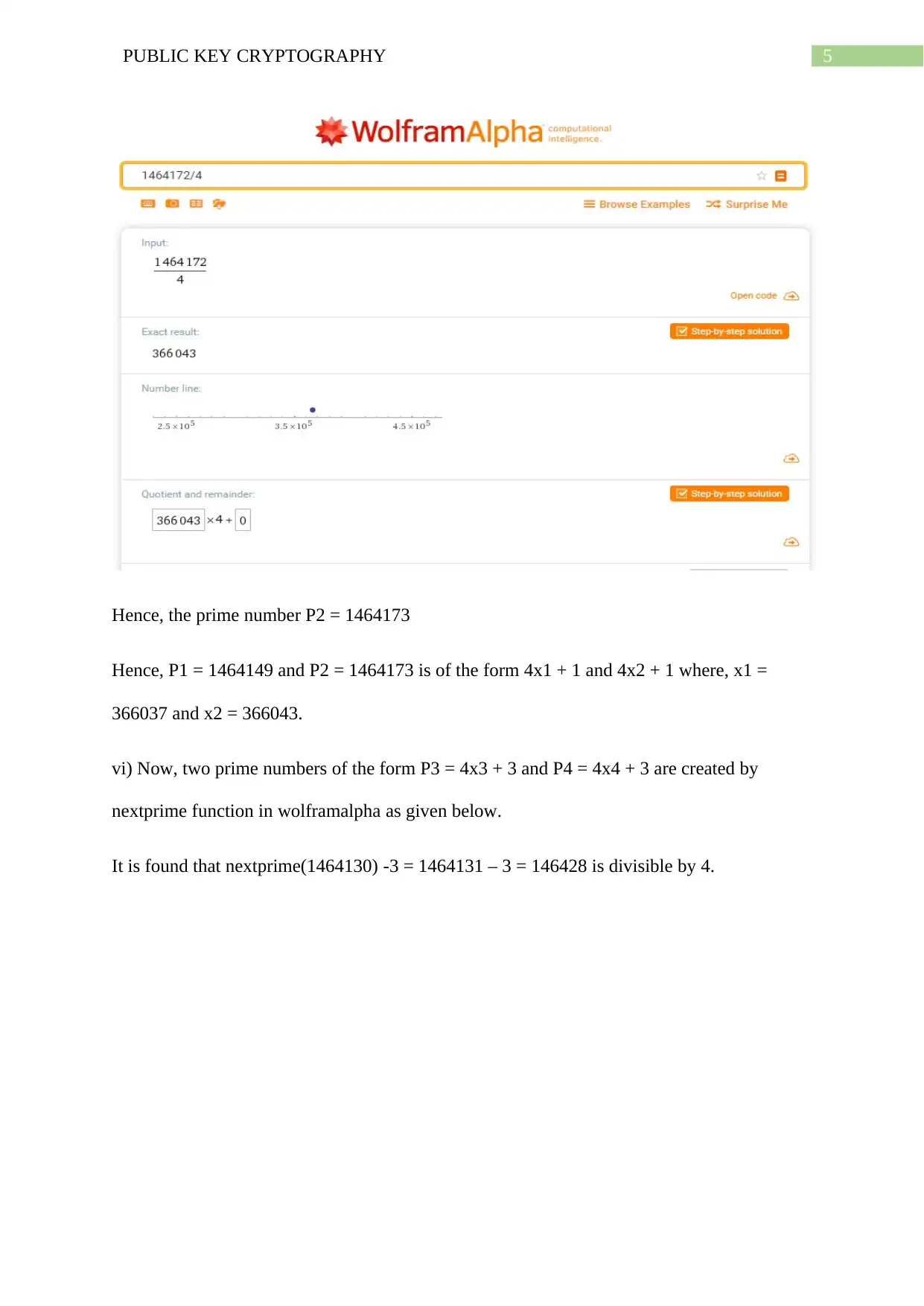
Hence, the prime number P2 = 1464173
Hence, P1 = 1464149 and P2 = 1464173 is of the form 4x1 + 1 and 4x2 + 1 where, x1 =
366037 and x2 = 366043.
vi) Now, two prime numbers of the form P3 = 4x3 + 3 and P4 = 4x4 + 3 are created by
nextprime function in wolframalpha as given below.
It is found that nextprime(1464130) -3 = 1464131 – 3 = 146428 is divisible by 4.

6PUBLIC KEY CRYPTOGRAPHY
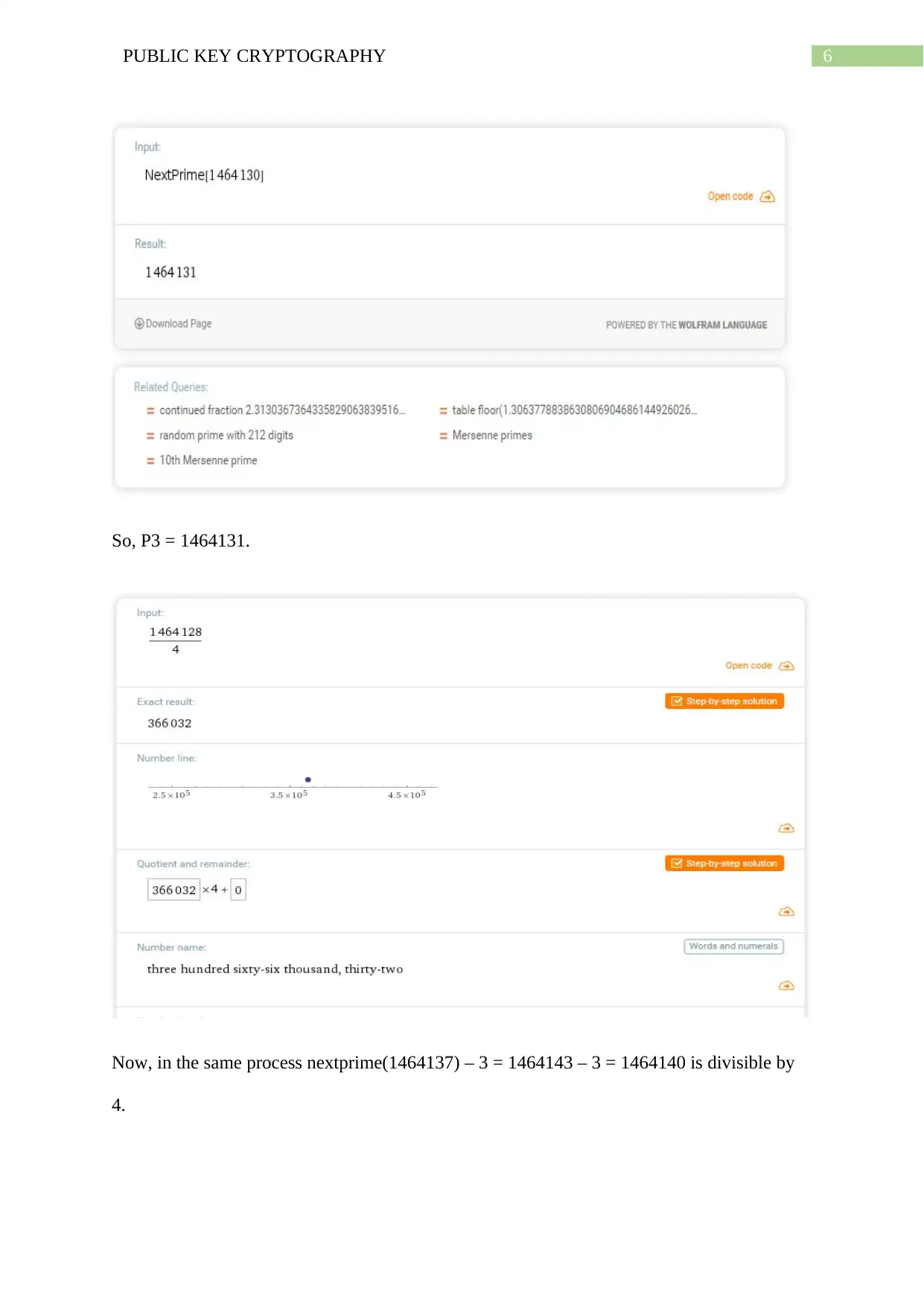
So, P3 = 1464131.
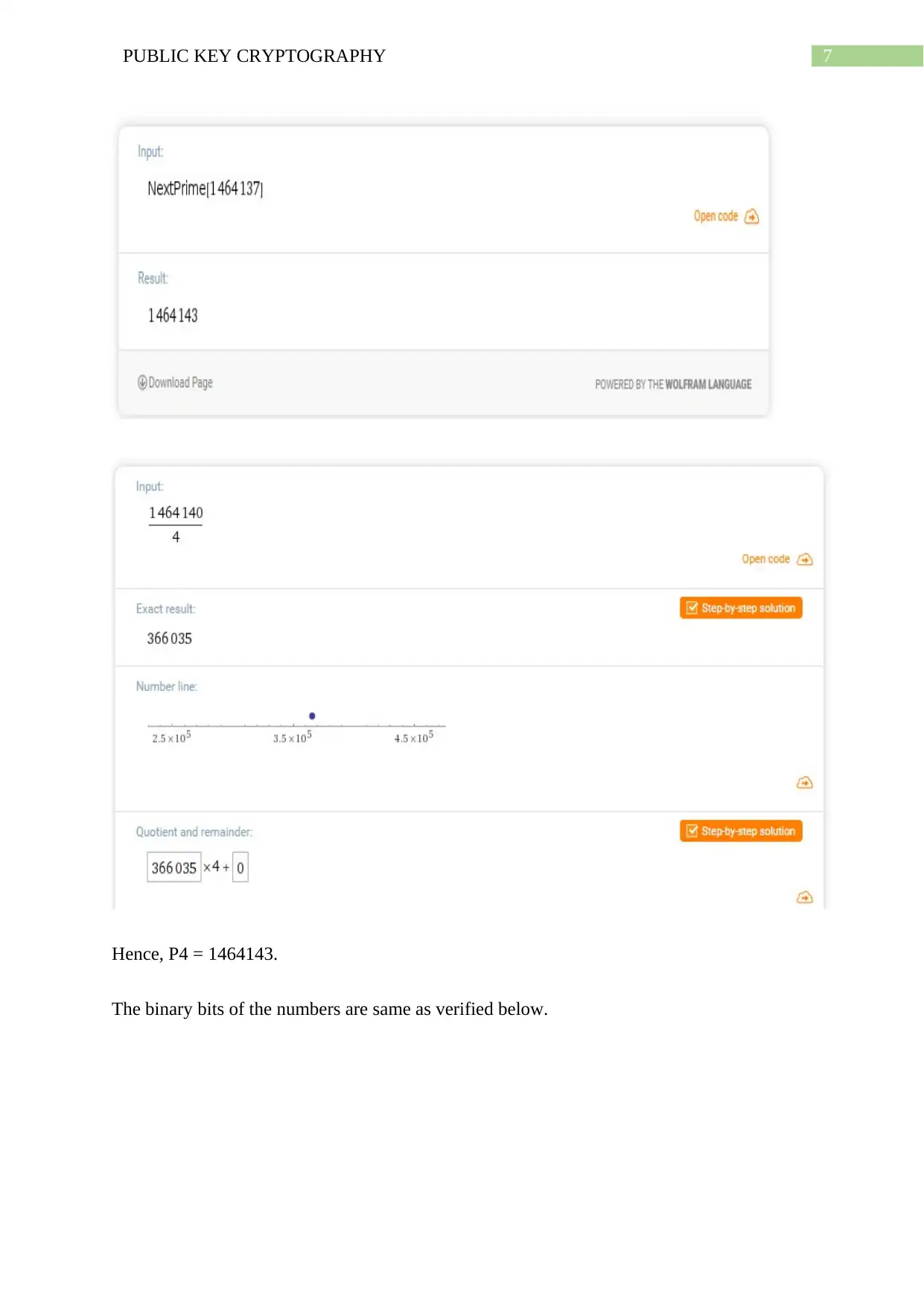
Now, in the same process nextprime(1464137) – 3 = 1464143 – 3 = 1464140 is divisible by
4.

7PUBLIC KEY CRYPTOGRAPHY
Hence, P4 = 1464143.
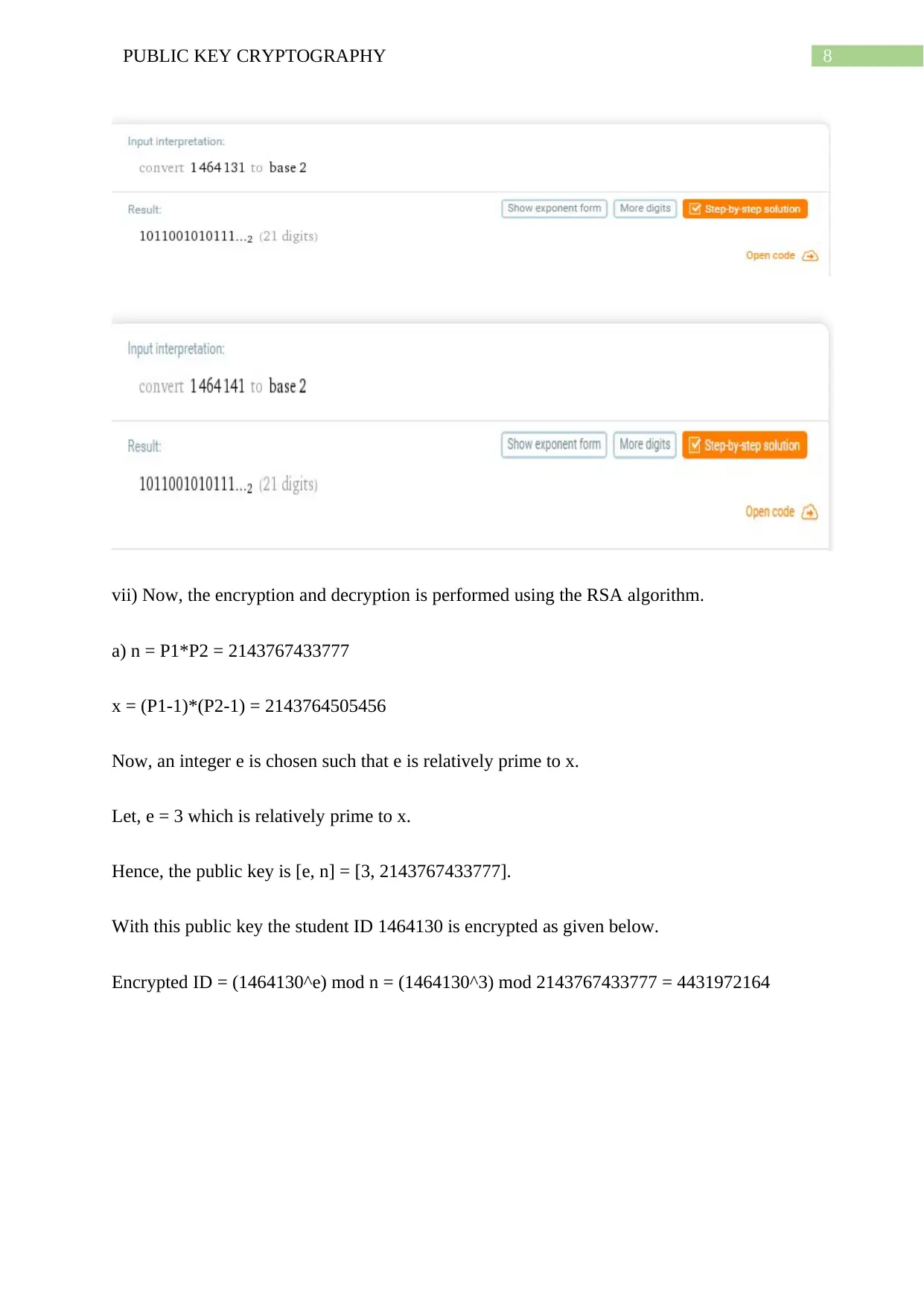
The binary bits of the numbers are same as verified below.

8PUBLIC KEY CRYPTOGRAPHY
vii) Now, the encryption and decryption is performed using the RSA algorithm.
a) n = P1*P2 = 2143767433777
x = (P1-1)*(P2-1) = 2143764505456
Now, an integer e is chosen such that e is relatively prime to x.
Let, e = 3 which is relatively prime to x.
Hence, the public key is [e, n] = [3, 2143767433777].
With this public key the student ID 1464130 is encrypted as given below.
Encrypted ID = (1464130^e) mod n = (1464130^3) mod 2143767433777 = 4431972164

9PUBLIC KEY CRYPTOGRAPHY
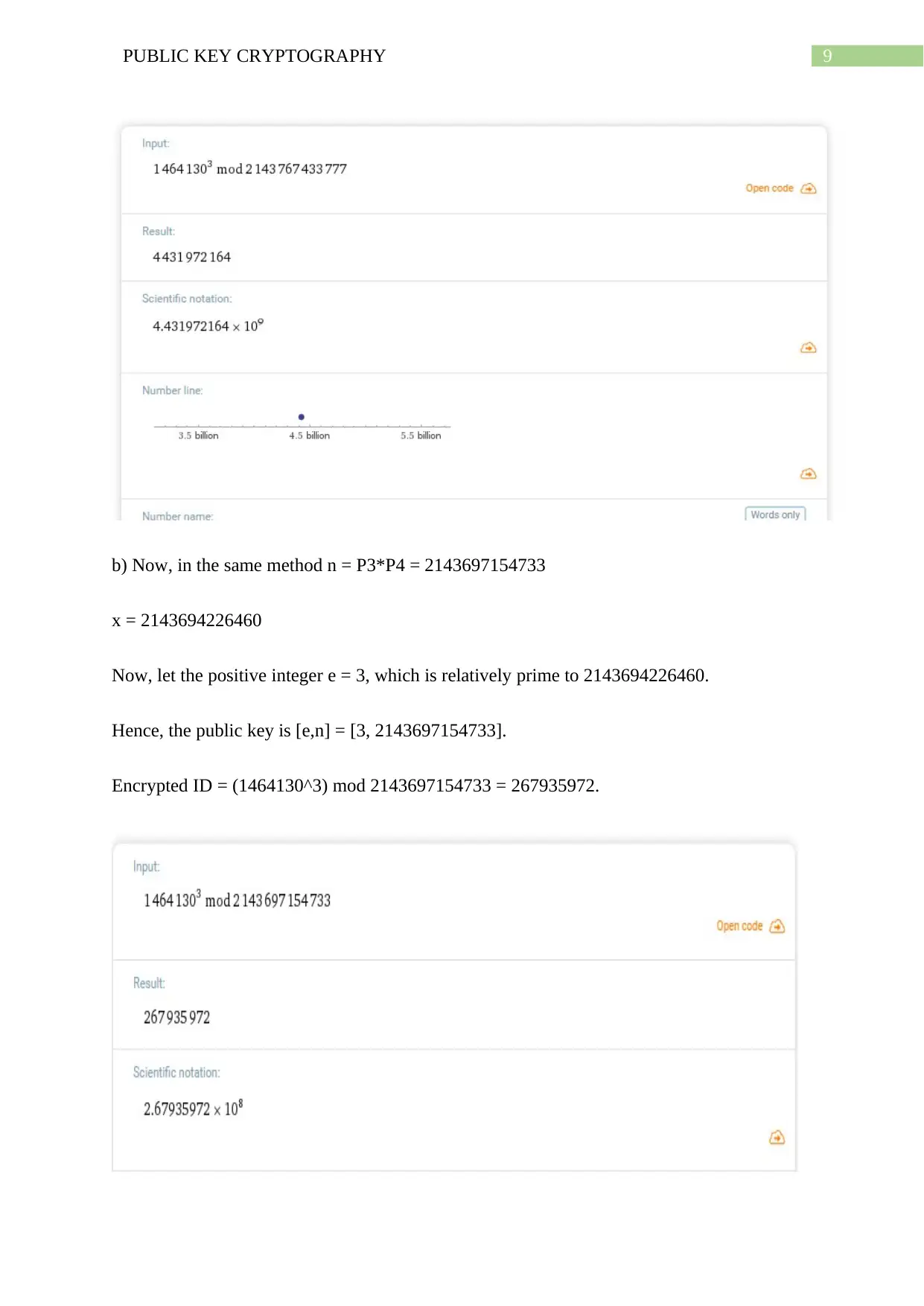
b) Now, in the same method n = P3*P4 = 2143697154733
x = 2143694226460
Now, let the positive integer e = 3, which is relatively prime to 2143694226460.
Hence, the public key is [e,n] = [3, 2143697154733].
Encrypted ID = (1464130^3) mod 2143697154733 = 267935972.

10PUBLIC KEY CRYPTOGRAPHY
viii)
Now, for decryption the private key is created for each of above two public keys.
Public key = [e, n] = [3, 2143767433777].
d is such that (d*e) mod x = 1
it is found that d = 18443.
After computation of d the private key is [d,n] = [18443, 2143767433777]
Now, using this private key the encrypted ID can be decrypted by the following method.
Original ID = ((Encrypted ID)^d) mod n = (4431972164^18443) mod 2143767433777 =
1464130.
Similarly, for public key [e,n] = [3, 2143697154733]
d is such that (d*e) mod x = 1 => d = 112826011919
private key = [d,n] = [112826011919, 2143767433777].
Using this ID also student ID 1464130 can be obtained.
Conclusion:
By, conclusion it can be said that the objectives of the assignment has been approximately
made as the private and public key generation in cryptography is successful as presented in
the example of the part 1. Furthermore, the generation process and algorithm is explained in
detail in a step by step manner as given in the part 1 solution. The public key cryptography is
a section of asymmetric cryptography which is popular cryptography method and this is
widely used modern day end to end encryption method for digital communication.

11PUBLIC KEY CRYPTOGRAPHY