Partial Fractions and Integration

This document explains the concept of partial fractions and integration. It provides step-by-step solutions for finding the partial fractions and evaluating the integral of a rational function. The domain and intercepts of the given function are also determined.

Q 1.
Answer
a)
i)
g(x, y) = D[x, y]0 = (2x, 7y)
By simple inspection, the transformation matrix A is found as
D = 2 0
0 7
This is verified as
g(x, y) = 2 0
0 7 · x
y = 2x
7y
D is a scaling matrix.
ii)
h(x, y) = B · [x, y]0 = (x, 3x + y)
By simple inspection, the transformation matrix B is found as
B = 1 0
3 1
This is verified as
h(x, y) = 1 0
3 1 · x
y = x
3x + y
B is a shearing matrix with y shearing factor of 3.
iii)
k(x, y) = C · [x, y]0 = (y, x)
By simple inspection, the transformation matrix C is found as
C = 0 1
1 0
1

This is verified as
k(x, y) = 0 1
1 0 · x
y = y
x
C is a reflection matrix through line y = x.
b)
The composition transformation required is
f = k ◦ h ◦ g
Applying the transformation to a vector x in R2. Therefore,
f (x) = (k ◦ h ◦ g)(x) = k(h(g(x)) = C(B(D · x))) = CBD(x)
Since, f (x) = A · x, we have
A = CBD
Matrix A is evaluated by matrix multiplication in the following way
A = CBD
= 0 1
1 0 × 1 0
3 1 × 2 0
0 7
= 0 1
1 0 × 2 0
6 7
= 6 7
2 0
c)
A transformation is invertible ifthe matrix oftransformation is invertible,
that is the matrix has a non zero determinant (Clark and Mccune, 2013).
A is the matrix of transformation f .It’s determinant is
det(A) = 6 7
2 0 = (6 × 0) − (2 × 14) = −14
2

Therefore, A is invertible.
Inverse of a 2d invertible matrix
M = a b
c d
is given by
M −1 = 1
det(M )
d −b
−c a
Therefore, inverse of A, which represents the transformation f−1 is
A−1 = − 1
14
0 −7
−2 6
d)
Let C0be a image in R2 to which the transformation f maps the unit circle C.
C0 = f(C)
Taking inverse on both sides
f −1(C0
) = C
Thus the inverse transformation maps the points on C0 back to the unit circle
C: x2 + y2 = 1.
Now, for a vector x in R2
f −1(x) = A−1 · x = −1
14
0 −7
−2 6 · x
y = − 1
14
−7y
−2x + 6y
This transformation maps back to the unit circle, therefore
− 1
14
(−7y)
2
+ − 1
14
(−2x + 6y)
2
= 1
Simplifying
49y2 + 36y2 − 24xy + 4x2 = 142
or
4x2 − 24xy + 85y2 = 142
3

is the required equation of the image f (C).
e)
Area of the image f (C) is obtained using a simple property of transformation
Area of f (C) = ||det(A)|| × Area of C
where, A is the matrix of transformation of f .
For the given transformation f ,determinant oftransformation matrix was
calculated (refer c) as:det(A) = −14,which implies ||det(A)|| = 14.Since
the area of unit circle C is π, therefore
Area of f(C) = 14 × π = 14π
Q 2.
Answer
a)
i)
f maps points (0,0), (1,0) and (0,1) into points (3,3), (3,4) and (4,3).
Let, x’ represent the transformed coordinates of point x.Therefore,
x’ = f(x) = A · x + a
Let A be any arbitrary matrix
A = a1 a2
b1 b2
and a be a vector [c1, c2]T .
For the transformation (0, 0) → (3, 3), we get
(3, 3)T = A · (0, 0)T + (c1, c2)T
Implies, (c1, c2)T = (3, 3)T .
For the transformation (1, 0) → (3, 4), we get
(3, 4)T = a1 a2
b1 b2
· (1, 0)T + (3, 3)T
4

Implies, a1 + 3 = 3 =⇒ a1 = 0 and b1 + 3 = 4 =⇒ b1 = 1.
For the transformation (0, 1) → (4, 3), we get
(4, 3)T = 0 a2
1 b2
· (0, 1)T + (3, 3)T
Implies, a2 + 3 = 4 =⇒ a2 = 1 and b2 + 3 = 3 =⇒ b2 = 0.
Therefore, the transformation f is completely determined as
f = 0 1
1 0 · (x, y)T + (3, 3)T
ii)
The are no fixed points visible in the transformation f .The transformation
is combination of translation,which happens 3 units along the line y = x,
as given by a and then reflection in the line y = x,as given by matrix A,
therefore, it is a case of glide-reflection.
b)
Reflection in the line y = −x + 5.
To achieve this transformation, the idea is to translate everything to the ori-
gin, reflect about the line y = −x and then move everything back.
Let us translate everything to origin using the transformation
x’ = x + h
where, h = (0, −5)T , is the translation vector.
Since we are at the origin, reflect in the line y = −x.This is achieved using
transformation matrix
A = 0 −1
−1 0
Therefore, the resulting transformation is
A(x + h) = 0 −1
−1 0 x + 0
−5 = 0 −1
−1 0 · x + 5
0
The final step is to move everything back to the originallocation which
is achieved by translating x by 5.This is achieved by the inverse vector
5

h−1 = (0, 5)T . Therefore, the final transformation k, is
k = A(x + h) + h−1 = 0 −1
−1 0 · x + 5
0 + 0
5 = 0 −1
−1 0 · x + 5
5
| {z }
Ax+b
which is the required form of the transformation k.
Q 3.
2x3 − 3x2 − 18x + 17
x2 − 3x − 4
Answer
a) Partial fractions
Since, for the given rational function, the degree of numerator is greater than
the degree of denominator, the function is first simplified by polynomial di-
vision in the following way
2x + 3
x2 − 3x − 4 2x3 − 3x2 − 18x + 17
2x3 − 6x2 − 8x ↓
3x2 − 10x + 17
3x2 − 9x − 12
− x + 29
Therefore, the rational function is simplified as
2x3 − 3x2 − 18x + 17
x2 − 3x − 4 = 2x + 3 + 29 − x
x2 − 3x − 4
In this simplified, partial fractions of only the last term (rational) has to be
determined.
6

Factorize x2 − 3x − 4 as (x − 4)(x + 1).
29 − x
x2 − 3x − 4
= 29 − x
(x − 4)(x + 1)
∴ 29 − x
(x − 4)(x + 1)
= A
x − 4+ B
x + 1
= A(x + 1) + B(x − 4)
(x − 4)(x + 1)
[Equating numerators]
29 − x = (A + B)x + (A − 4B)
[Equating coefficients of like terms on both sides]
29 = A − 4B (1)
−1 = A + B (2)
[(1) and (2) are solved simultaneously]
A = 5 & B = 6
∴ 2x3 − 3x2 − 18x + 17
x2 − 3x − 4 = 2x + 3 + 5
x − 4− 6
x + 1
b)
c)
Integral to be evaluated is
Z 2x3 − 3x2 − 18x + 17
x2 − 3x − 4 dx
7

In order to evaluate the integral, the rational fraction is first expressed in the
partial fraction as obtained in part a).Therefore,
Z 2x3 − 3x2 − 18x + 17
x2 − 3x − 4 dx =
Z
2x + 3 + 5
x − 4− 6
x + 1dx
[Taking integration to individual terms]
=
Z
2x dx +
Z
3 dx +
Z 5
x − 4dx −
Z 6
x + 1dx
[
Z
xn = xn+1
n + 1 =⇒
Z
2x = x2]
[
Z
k = kc =⇒
Z
3 = 3x]
= x2 + 3x +
Z 5
x − 4dx −
Z 6
x + 1dx
[Substitute: x − 4 = u & x + 1 = v]
= x2 + 3x + 5
Z 1
u du − 6
Z 1
v dv
[Standard Int.:
Z 1
x = ln x]
= x2 + 3x + 5 ln u − 6 ln v + C
[Back substitute: u = x − 4 & v = x + 1]
∴
Z 2x3 − 3x2 − 18x + 17
x2 − 3x − 4 dx = x2 + 3x + 5 ln (x − 4) − 6 ln (x + 1) + C
Q 4.
f (x) = x + 1
x2 + 8
Answer
a) Domain and intercept
8

Domain :For a function of single variable x, domain is the set of all inputs
for which the function f (x) is well defined.
Since for the given f (x),the denominator is always positive and never be-
comes 0, the function is set of all real numbers R.
Domain of f (x):(−∞, ∞)
Intercepts:The x- intercept(s) of f (x) is obtained by setting f (x) = 0 and
the y- intercept of f (x) is obtained by setting x = 0 in f (x).
x- intercept:
f (x) = 0
=⇒ x + 1
x2 + 8= 0
[x2 + 8 6= 0]
∴ x + 1 = 0 =⇒ x = −1
Therefore, x = −1 or (−1, 0) is the x- intercept.
y- intercept:
f (x) = 0 + 1
0 + 8= 1
8
Therefore, y =1
8 or 0,1
8 is the y- intercept.
b) Find f0
(x)
f (x) = x + 1
x2 + 8
Since f (x) is rational function, use Product Rule to find the derivative:
Product Rule :d
dx
u
v = vu0− uv0
v2
9

For the given f (x), u = x + 1 and v = x2 + 8.Therefore
f 0
(x) = (x2 + 8)(x + 1)0− (x + 1)(x2 + 8)0
(x2 + 8)2
[Derivatives : (x + 1)0 = 1 & (x 2 + 8)0 = 2x]
= (x2 + 8) − (x + 1)(2x)
(x2 + 8)2
= x2 + 8 − 2x2 − 2x
(x2 + 8)2
∴ f 0
(x) = 8 − x2 − 2x
(x2 + 8)2
c) Stationary points
Stationary point(s) of a function f (x) is determined by setting f0
(x) = 0.
For the given f (x), we have
f 0
(x) = 8 − x2 − 2x
(x2 + 8)2
For the stationary points therefore
f 0
(x) = 0
=⇒ 8 − x2 − 2x
(x2 + 8)2 = 0
[The denominator: (x2 + 8)2 > 0]
=⇒ 8 − x2 − 2x = 0
(x + 4)(x − 2) = 0
∴ x = −4 or x = 2
For x = −4,
f (x) = −4 + 1
16 + 8
= −0.125
For x = 2,
f (x) = 2 + 1
4 + 8
= 0.25
10

The stationary points of f (x) therefore are:(−4, −0.125) and (2, 0.25).
x x < −4 : x = −5−4 < x < 2 : x = 0x > 2 : x = 3
f 0
(x) −6.43 × 10−3 0.125 −0.024
From the sign of f0
(x) it is clear that f (x) is decreasing in the interval x < −4,
then increasing in the interval −4 < x < 2 and then decreasing for x > 2.
This suggests that x = −4 or the point (−4, −0.125) is absolute minimum of
f (x) and x = 2 or the point (2, 0.25) is absolute maximum (Stewart, Redlin,
Watson and Panman, 2017).
d) Equation of asymptotes
Vertical asymptote:Equation of vertical asymptote of a rational function
is obtained by setting the denominator equal to 0.
For the given f (x), the denominator x2 + 8 has no real roots, therefore, f (x)
has no vertical asymptotes.
Horizontalasymptote:Equation of horizontalasymptote is obtained by
solving the limit
lim
x→∞ f (x)
For the given f (x)
lim
x→∞ f (x) = lim
x→∞
x + 1
x2 + 8= lim
x→∞
1
x + 1
x2
1 + 8
x2
= 0
The horizontal asymptote of f (x) therefore is y = 0, or the x- axis.
e) Odd, even or neither
A function g(x) is odd if g(−x) = −g(x), or even if g(−x) = g(x), or neither
if both conditions are false.For the given function f (x)
f(−x) = (−x) + 1
(−x)2 + 8= −x + 1
x2 + 8
f (−x) 6= −f (x), also f (−x) 6= f (x).Therefore, f (x) is neither odd nor even.
f ) Sketch of f (x)
11

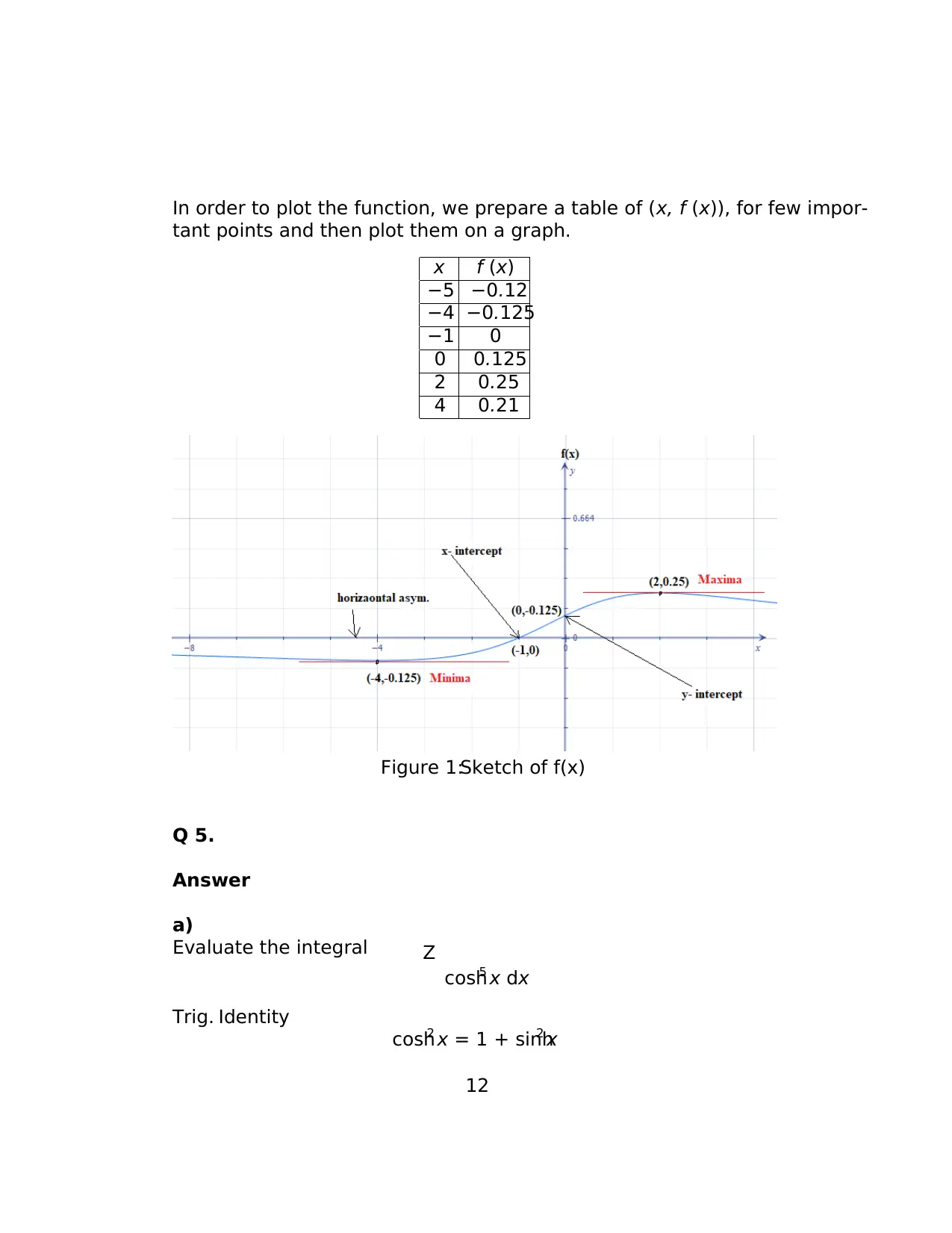
In order to plot the function, we prepare a table of (x, f (x)), for few impor-
tant points and then plot them on a graph.
x f (x)
−5 −0.12
−4 −0.125
−1 0
0 0.125
2 0.25
4 0.21
Figure 1:Sketch of f(x)
Q 5.
Answer
a)
Evaluate the integral Z
cosh5 x dx
Trig. Identity
cosh2 x = 1 + sinh2 x
12

Therefore,
Z
cosh5 x dx =
Z
cosh x(cosh2 x)2 dx
=
Z
cosh x(1 + sinh2 x)2 dx
[Substitute:sinh x = u =⇒ cosh x dx = du]
=
Z
(1 + u2)2 du
=
Z
1 + 2u2 + u4 du
[Standard Int. :
Z
un = un+1
n + 1
]
= u + 2
u3
3 + u5
5 + C
[Back substitute:u = sinh x]
∴
Z
cosh5 x dx = sinh x +
2 sinh3 x
3 + sinh5 x
5 + C
b)
Integral to be evaluated is
Z x5
√ x2 − 16dx [x > 4]
To evaluate the integral, we make the following substitution
x = 4 cosh u
This implies
dx = 4 sinh u du
13

Therefore
Z x5
√ x2 − 16dx =
Z 45 cosh5 u
p 16 cosh2 u − 16
· 4 sinh u du
= 45
Z cosh5 u
p cosh2 u − 1 sinh u du
[Trig. Identity: sinh2 u = cosh2 u − 1]
= 1024
Z cosh5 u
sinh u sinh u du
= 1024
Z
cosh5 u du
[Using the result for
Z
cosh5 x dx, from part a)]
∴ = 1024 sinh u +
2 sinh3 u
3 + sinh5 u
5 + C
[Back substitute: u = cosh−1 x
4 ]
= 1024 sinhcosh−1 x
4 + 2 × 1024 sinh3 cosh−1 x
4
3
+ 1024 sinh5 cosh−1 x
4
5 + 1024C
[Trig. Property:sinh cosh−1 x
4 =
√ x2 − 16
4 , for positive x]
[Trig. Property:sinh3 cosh−1 x
4 = (x2 − 16)3/2
64 , for positive x]
[Trig. Property:sinh5 cosh−1 x
4 = (x2 − 16)5/2
1024 , for positive x]
∴ = 1024
√ x2 − 16
4 + 2 × 1024
3 × 64(x2 − 16)3/2 + 1
1024 × 5
(x2 − 16)5/2 + C0
[where, C0 = 1024C]
∴
Z x5
√ x2 − 16dx = 256
√ x2 − 16 +
32
3 (x2 − 16)3/2 + (x2 − 16)5/2
5 + C0
14

Q 6.
dx
dt = t
(t2 + 1)1/3
Answer
a)
Since the Differential equation is of the form
dx
dt = p(x)
q(t)
we can apply the Variable Separable method to solve it.
b)
The DE is solved in the following way
dx
dt = t
(t2 + 1)1/3
[Separating variables]
dx = t
(t2 + 1)1/3 dt
[Integrating both sides]
Z
dx =
Z t
(t2 + 1)1/3 dt
[Substitute: t2 + 1 = u =⇒ 2t dt = du]
Z
dx = 1
2
Z du
u1/3
[Standard Int.
Z
un = un+1
n + 1
]
∴ x = 1
2
u2/3
2/3 + C
[Back substitute: u = t2 + 1]
15

∴ x(t) = 3
4(t2 + 1)2/3 + C
c)
Initial condition:x(0) = 1.Therefore, substituting t = 0 in the solution for
x(t) (refer part b):
x(0) = 1 =
3
4((0)2 + 1)2/3 + C = 3
4 + C
Implies, C = 1 −3
4 = 1
4. Therefore, the particular solution is
x(t) = 3
4(t2 + 1)2/3 + 1
4
Q 7.
dy
dt = −et+y, [t ≥ 0]
Answer
a)
Using property of exponential functions
ea+b = ea · eb
the DE is simplified as dy
dt = −ey et
This is similar to the form
dy
dt = p(y) q(t)
which is solved using Variable Separable method.
16

b)
The DE is solved in the following way
dy
dt = −ey et
[Separating Variables]
dy
ey = −et dt
[Integrating both sides]
Z dy
ey = −
Z
et dt
[Standard Int.
Z
eax = eax
a ]
∴ e−1
−1 = −et + C
e−y = et + C
[Taking log on both sides]
−y = ln (et + C)
∴ y(t) = − ln (et + C)
c)
Initial condition:y(0) = 2.Therefore, substituting t = 0 in the solution for
y(t) (refer part b):
y(0) = 2 = − ln (e0 + C) = − ln (1 + C)
Implies,
ln (1 + C) = −2 =⇒ 1 + C = e−2 =⇒ C = e−2 − 1
Therefore, the particular solution is
y(t) = − ln (et + e−2 − 1)
Q 8.
dy
dx = 3y
x + 1
17

Answer
a)
The given DE has a form similar to
dy
dx + p(x)y = q(x)
with, p(x) = −3
x and q(x) = 1.
It is therefore a linear first order differentialequation whose solution is de-
termined the method of Integrating factor.
b)
Begin with the DE expressed correctly in the form of linear first order DE:
dy
dx − 3y
x = 1 (1)
Comparing with the standard form oflinear first order DE,p(x) = − 3
x .
Therefore, the integrating factor is
μ(x) = e
R p(x) dx = e−3R 1
x dx = e−3 ln x= eln( 1
x3 ) = 1
x3
Multiply (1) throughout by (x)
1
x3
dy
dx − 3y
x4 = 1
x3
The left side is an exact differential ofy
x3 , that is
d
dx
y
x3 = 1
x3
dy
dx − 3y
x4
18

Therefore,
d
dx
y
x3 = 1
x3
[Integrating both sides]
Z d
dx
y
x3 =
Z 1
x3
[Fundamental Theorem:
Z d
dxf = f ]
[Standard Int. :
Z
xn = xn+1
n + 1
]
=⇒ y
x3 = − 1
2x2 + C
∴ y(x) = Cx3 − x
2
Q 9.
dv
dx = k
v
Answer
a)
The DE is dv
dx = k
v, [k, v > 0& x ≥ 0]
Denote the starting point of the object as x0. The coordinate system can be
fixed at x0 such that origin (0, 0) is the starting point and when the object
moves away from the starting point, the change in distance is x − x0 = x.
19

The DE is solved in the following way
dv
dx = k
v
[Separating variables]
v dv = k dx
Integrating both sides
Z
v dv = k
Z
dx
∴ v2
2 = kx + C
[Expressing in implicit form]
v(x) =√ 2kx + C0 [where,C0 = 2C]
b)
The speed of the object at the starting point is 10 m/s, that is when x = 0,
the speed v = 10.Implies,
v(0) = 10 =
p 2k(0) + C0 = √ C0 =⇒ C 0 = 100
The particular solution therefore is
v(x) =√ 2kx + 100
c)
When x = 5, the speed v = 20 m/s.Therefore,
20 =p 2k(5) + 100 =⇒ 400 = 10k + 100 =⇒ k = 30
Therefore, the complete solution for speed is
v(x) =√ 60x + 100
d)
When v = 40, the corresponding position of object is determined as
40 =√ 60x + 100 =⇒ 1600 = 60x + 100 =⇒ x = 25
20

Therefore, the object is 25 m away from the starting point when its speed is
40 m/s.
e)
References:
B, G., Hass,J., Heil, C. R. and Weir,M. D. (2018). Thomas’calculus:
multivariable.Boston:Pearson.
Blitzer, R. (2019).Thinking mathematically (7th ed.).Boston:Pearson.
Clark, W. D. and Mccune,S. K. (2013).Linear algebra.New York,New
York: Mcgraw Hill.
Grewal,B. (2017). Advanced Engineering Mathematics.India: Mercury
LearningInformation.
21

Hoffman,K. and Kunze,R. (2015). Linear algebra.Noida,U.P., India:
Pearson India Education Services.
Lipschutz, S. and Lipson, M. (2018).Linear algebra.New York:Mcgraw-Hill
Education.
Maruskin, J. M. (2014).Integralcalculus.San Jose, California:Solar Crest
Publishing, Llc.
Stewart, J. (2019).Calculus:concepts and contexts.Boston, Ma, Usa:Cen-
gage.
Stewart,J., Redlin, L., Watson,S. and Panman,P. (2017). Precalculus:
mathematics for calculus.Australia:Cengage Learning.
Sullivan, M. (2019).Precalculus.Hoboken, NJ: Pearson.
22