Statistical Process Control Analysis

This assignment delves into the realm of statistical process control, examining various techniques and their applications. It includes a detailed analysis of data sets, investigating normality assumptions, determining process capability, and constructing control charts (I-MR, Cusum, EWMA). The analysis aims to assess process stability and identify potential deviations from desired performance standards. The assignment also explores the use of transformed variables (e.g., square root and natural logarithm) to address non-normality in data.

Quality Systems Design
Name
University
8th October 2017

Question 1:
a) Answers
Descriptive Statistics: Pb1_Workhours
Variable Mean StDev Minimum Q1 Median Q3 Maximum
Pb1_Workhours 122.18 15.89 97.00 111.00 120.00 132.25 162.00
The above results shows that the mean is 122.18 while the median is 120. The standard
deviation is 15.89. The values shows that the data is close to normally being distributed.
We can therefore say that the data is normally distributed.
b) Answer
The stem and leaf plot below;
Stem-and-leaf plot (Pb1_Workhours):
Unit: 10
9 7 8 8
10 0 0 3 5 7 8 9 9
11 1 1 2 2 2 3 3 4 6 6 7 8 9
12 0 0 2 2 4 4 4 8 8 8
13 1 1 1 2 3 3 5 6 8 8
14 2 6
15 0 5 8
16 2
The shape and distribution of the stem-and-leaf plot shows that the data is normally
distributed.
c) Answer
Histogram

The histogram above suggest that the data is normally distributed
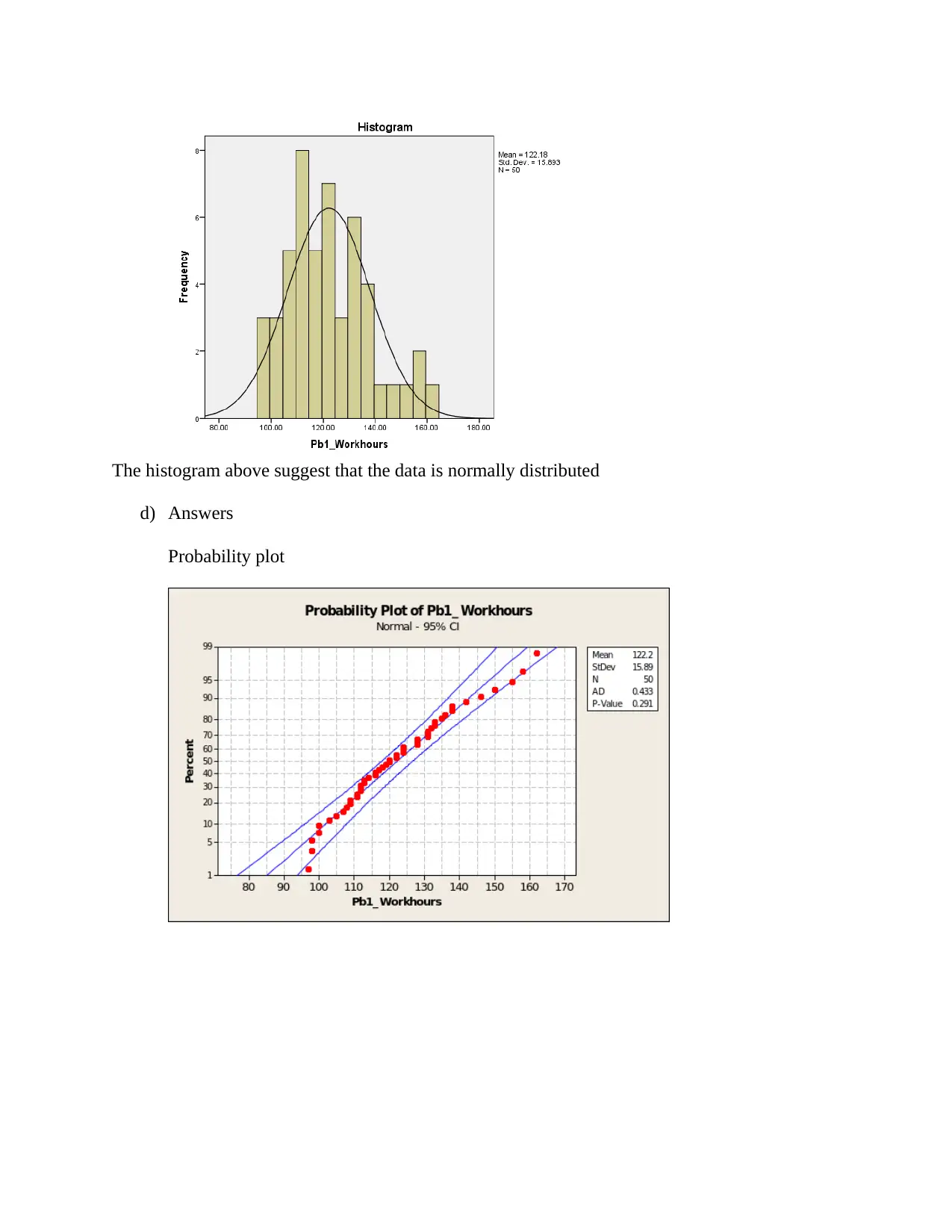
d) Answers
Probability plot

Question 2:
a) Hypothesis
The hypothesis for the given test is;
H0 : μA =μB
H A : μA ≠ μB
That is;
H0: The before is the same as the mean after
HA: The before is not the same as the mean after
b) Interpretation of the p-value;
Paired T-Test and CI: Pb2_Before, Pb2_After
Paired T for Pb2_Before - Pb2_After
N Mean StDev SE Mean
Pb2_Before 10 5.03200 0.58309 0.18439
Pb2_After 10 5.52600 0.44257 0.13995
Difference 10 -0.494000 0.881542 0.278768
95% CI for mean difference: (-1.124617, 0.136617)
T-Test of mean difference = 0 (vs not = 0): T-Value = -1.77 P-Value = 0.110
The p-value is given as 0.110 (a value greater than 5% level of significance0, we
therefore fail to reject the null hypothesis and conclude that the mean completion
times before and after are not significantly different.

Question 3:
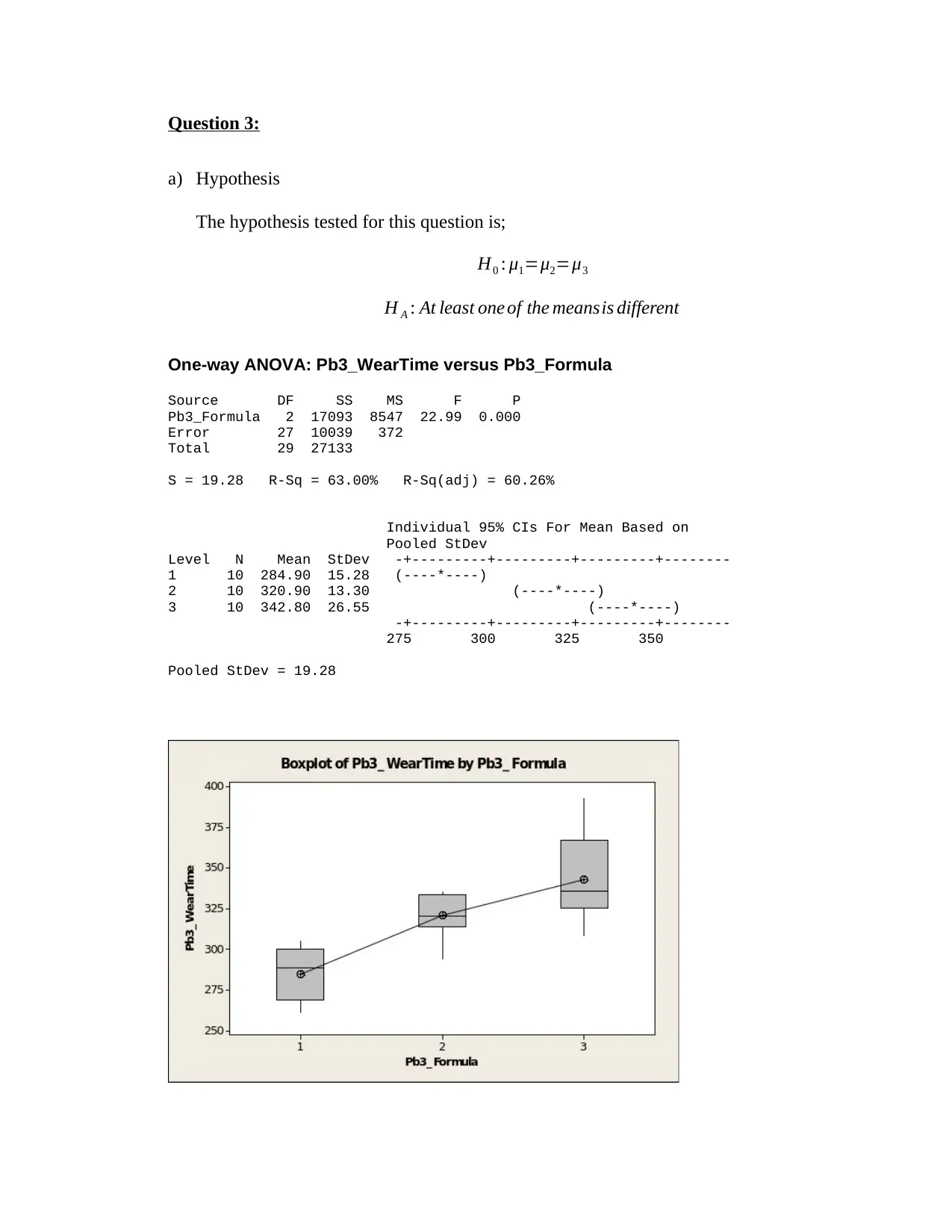
a) Hypothesis
The hypothesis tested for this question is;
H0 : μ1=μ2=μ3
H A : At least one of the meansis different
One-way ANOVA: Pb3_WearTime versus Pb3_Formula
Source DF SS MS F P
Pb3_Formula 2 17093 8547 22.99 0.000
Error 27 10039 372
Total 29 27133
S = 19.28 R-Sq = 63.00% R-Sq(adj) = 60.26%
Individual 95% CIs For Mean Based on
Pooled StDev
Level N Mean StDev -+---------+---------+---------+--------
1 10 284.90 15.28 (----*----)
2 10 320.90 13.30 (----*----)
3 10 342.80 26.55 (----*----)
-+---------+---------+---------+--------
275 300 325 350
Pooled StDev = 19.28

b) Plot and analysis of residuals
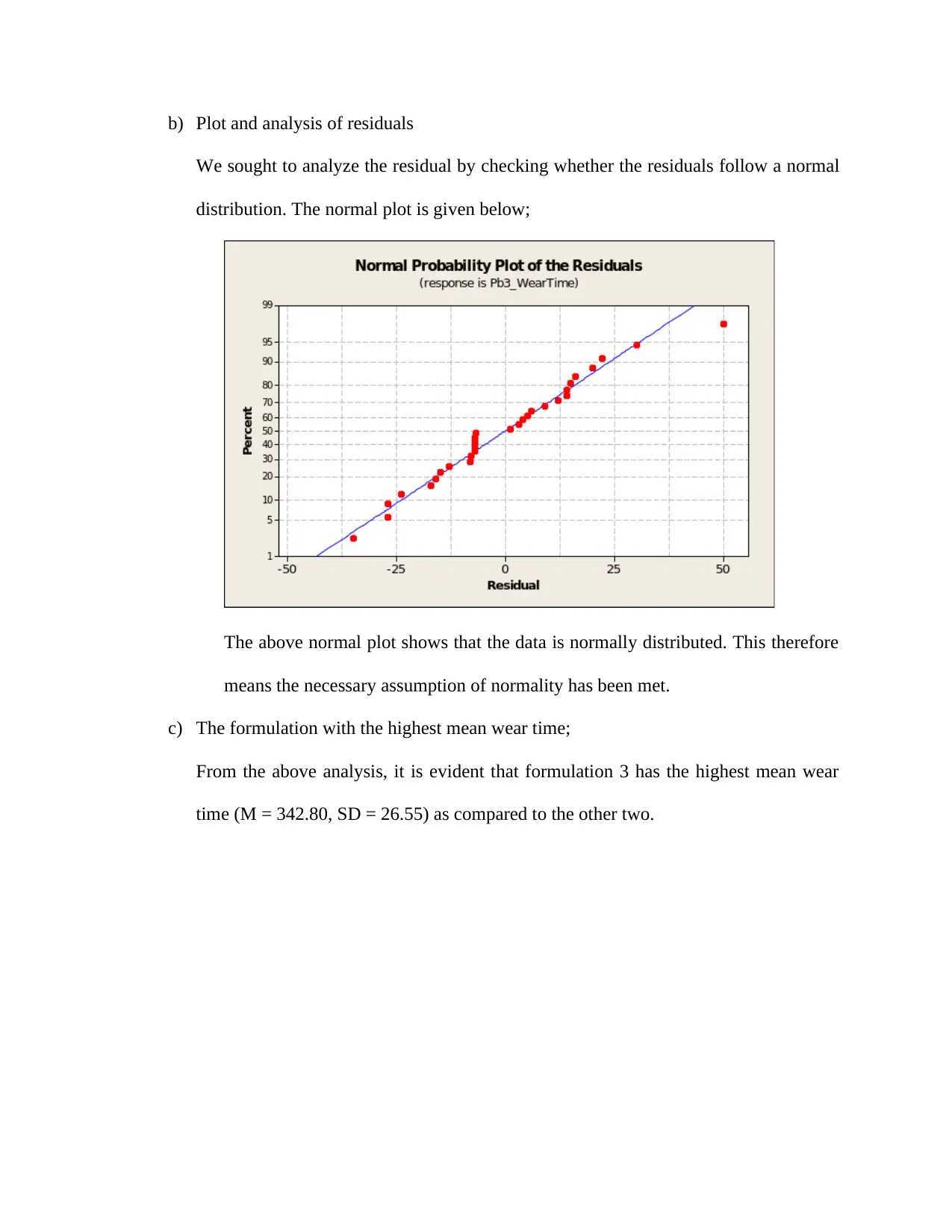
We sought to analyze the residual by checking whether the residuals follow a normal
distribution. The normal plot is given below;
The above normal plot shows that the data is normally distributed. This therefore
means the necessary assumption of normality has been met.
c) The formulation with the highest mean wear time;
From the above analysis, it is evident that formulation 3 has the highest mean wear
time (M = 342.80, SD = 26.55) as compared to the other two.

Question 4:
a) Hypothesis of the question
The hypothesis to be tested for this question is;
H0: β1 = β2 = β3 = 0
H1: At least one β is not zero
Regression results;
Regression Analysis: Pb4_Volume versus Pb4_Diameter, Pb4_Length, .
The regression equation is
Pb4_Volume = - 36.3 + 30.5 Pb4_Diameter + 4.77 Pb4_Length + 1.25 Pb4_Cycles
Predictor Coef SE Coef T P
Constant -36.2579 0.4677 -77.52 0.000
Pb4_Diameter 30.4946 0.5778 52.77 0.000
Pb4_Length 4.76576 0.00922 516.84 0.000
Pb4_Cycles 1.25134 0.01009 124.04 0.000
S = 0.00841452 R-Sq = 100.0% R-Sq(adj) = 100.0%
Analysis of Variance
Source DF SS MS F P
Regression 3 19.8206 6.6069 93311.67 0.000
Residual Error 29 0.0021 0.0001
Total 32 19.8226
Source DF Seq SS
Pb4_Diameter 1 0.7936
Pb4_Length 1 17.9376
Pb4_Cycles 1 1.0894
Unusual Observations
Obs Pb4_Diameter Pb4_Volume Fit SE Fit Residual St Resid
5 0.799 10.6639 10.6443 0.0039 0.0196 2.62R
6 0.791 12.4260 12.4243 0.0054 0.0017 0.26 X
17 0.796 10.2603 10.2819 0.0040 -0.0216 -2.93R
22 0.796 11.1412 11.1264 0.0046 0.0148 2.11R
30 0.801 12.8889 12.8726 0.0029 0.0163 2.06R
R denotes an observation with a large standardized residual.
X denotes an observation whose X value gives it large influence.

b) Analyzing residuals
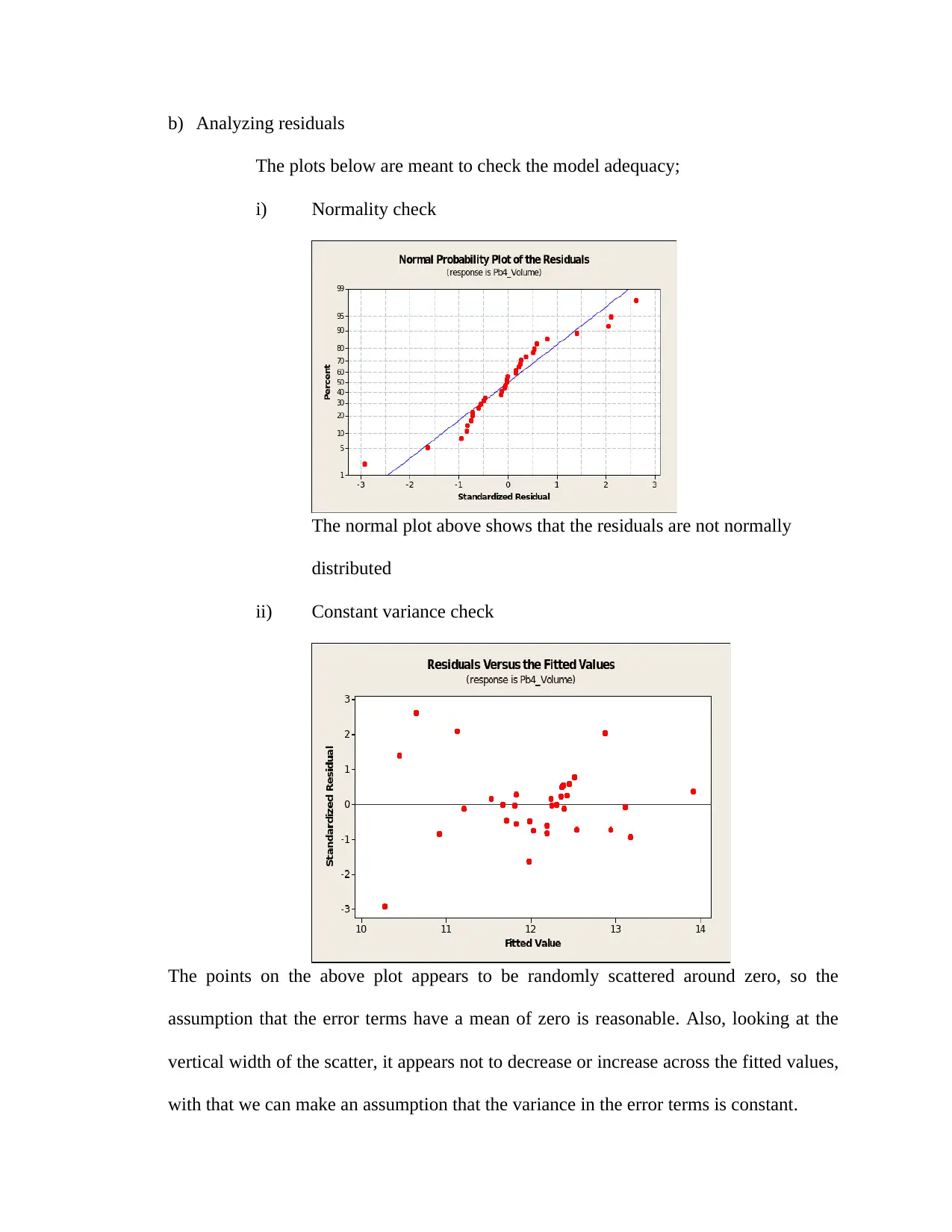
The plots below are meant to check the model adequacy;
i) Normality check
The normal plot above shows that the residuals are not normally
distributed
ii) Constant variance check
The points on the above plot appears to be randomly scattered around zero, so the
assumption that the error terms have a mean of zero is reasonable. Also, looking at the
vertical width of the scatter, it appears not to decrease or increase across the fitted values,
with that we can make an assumption that the variance in the error terms is constant.

Question 5:
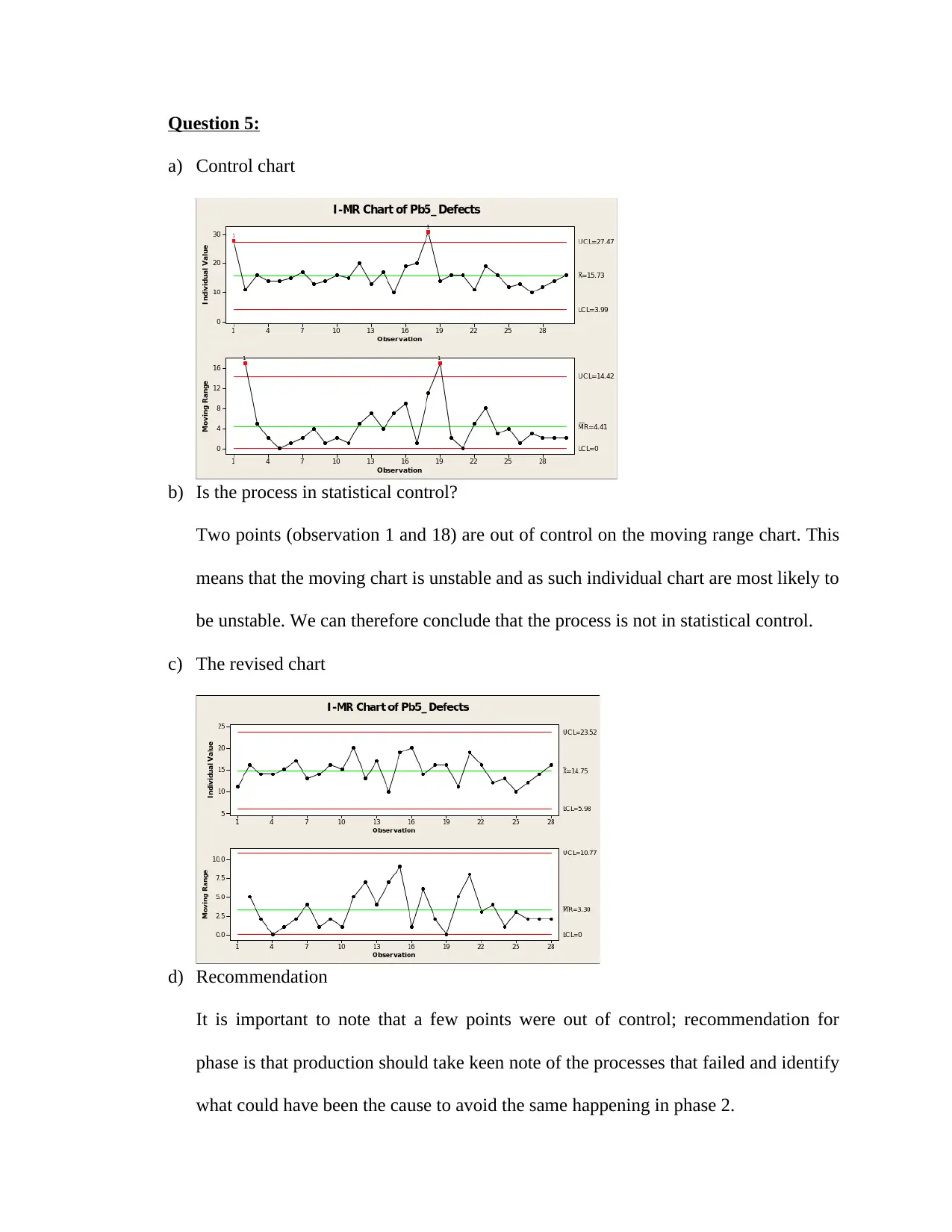
a) Control chart
b) Is the process in statistical control?
Two points (observation 1 and 18) are out of control on the moving range chart. This
means that the moving chart is unstable and as such individual chart are most likely to
be unstable. We can therefore conclude that the process is not in statistical control.
c) The revised chart
d) Recommendation
It is important to note that a few points were out of control; recommendation for
phase is that production should take keen note of the processes that failed and identify
what could have been the cause to avoid the same happening in phase 2.

Question 6:
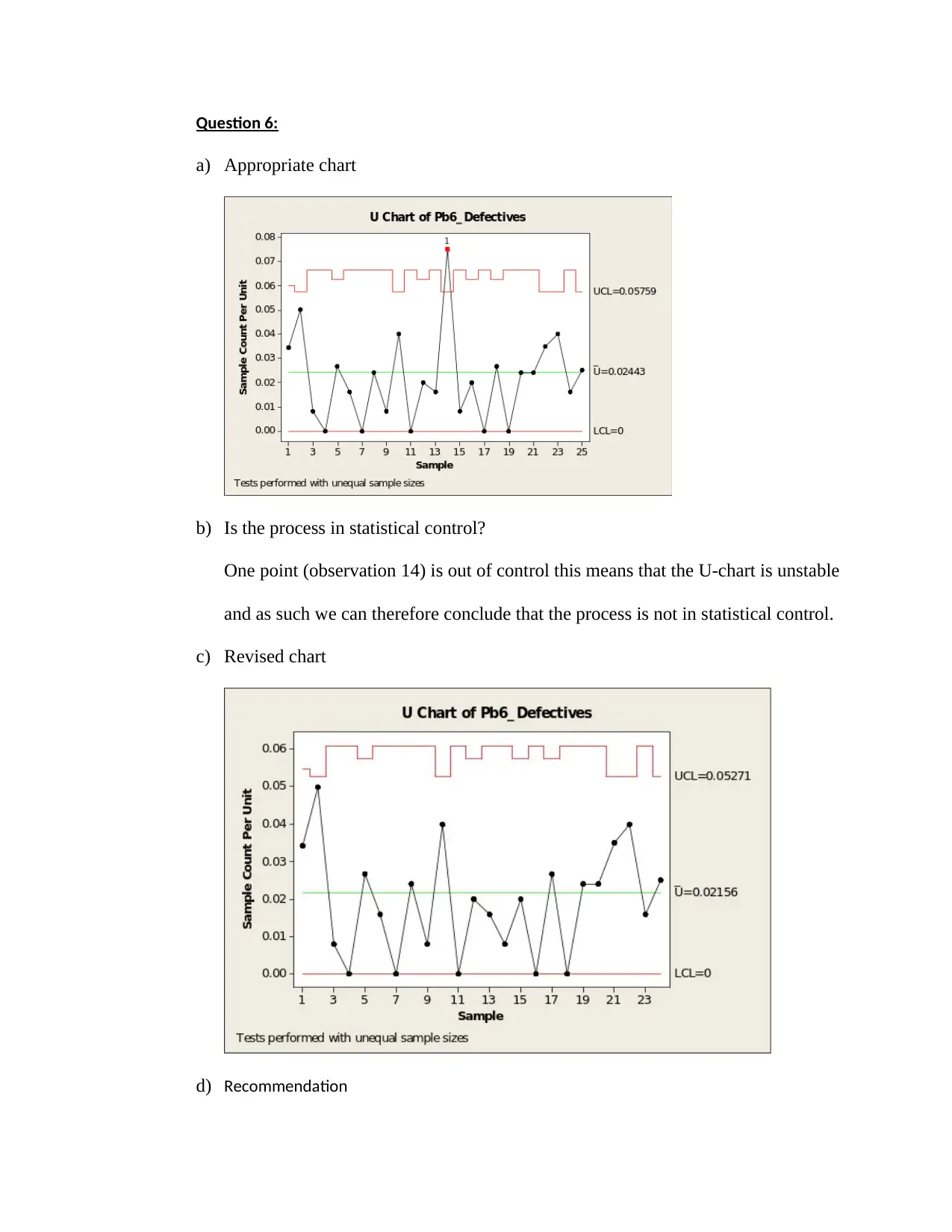
a) Appropriate chart
b) Is the process in statistical control?
One point (observation 14) is out of control this means that the U-chart is unstable
and as such we can therefore conclude that the process is not in statistical control.
c) Revised chart
d) Recommendation

The process in is control and as such the production should continue with the current
production without alteration.
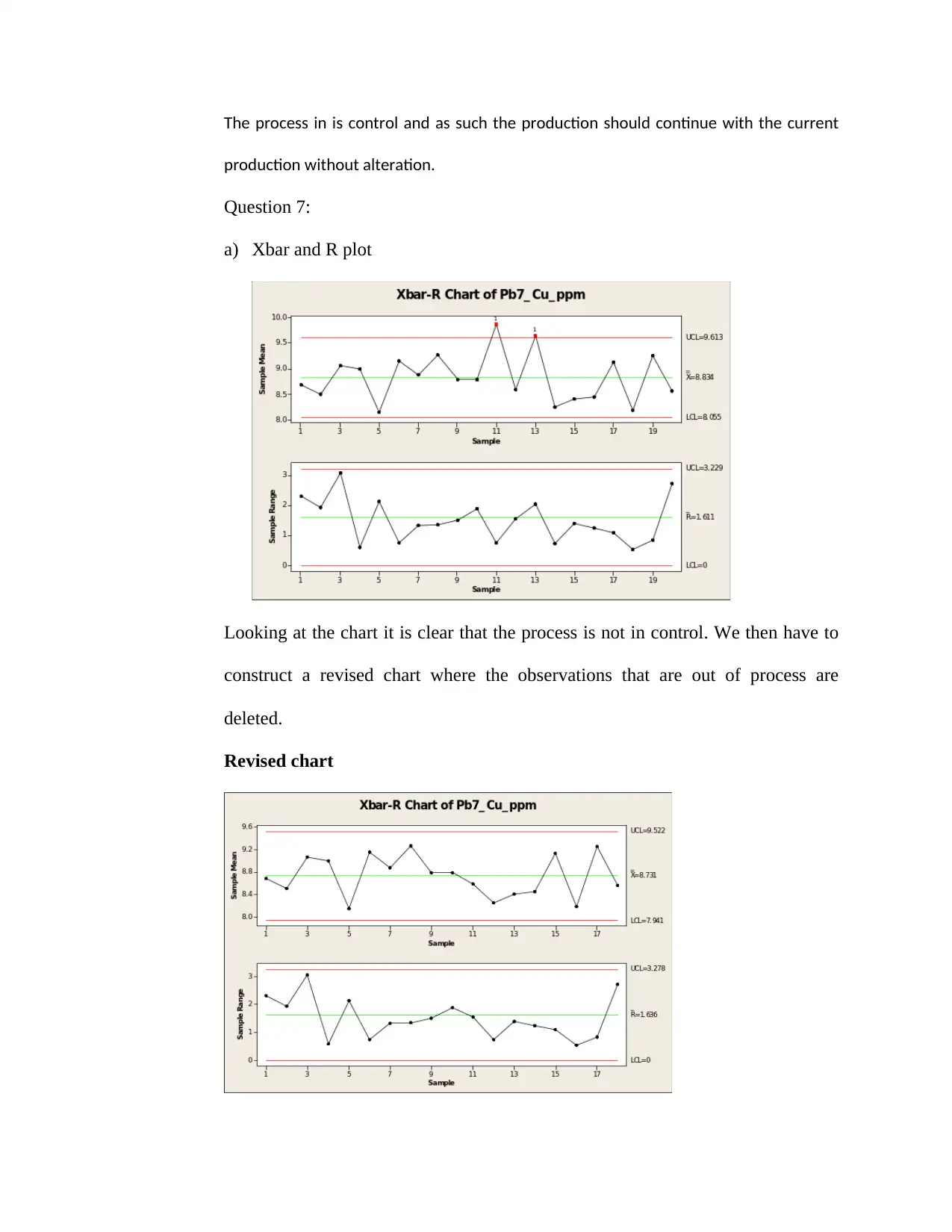
Question 7:
a) Xbar and R plot
Looking at the chart it is clear that the process is not in control. We then have to
construct a revised chart where the observations that are out of process are
deleted.
Revised chart

b) Mean and standard deviation of the revised process is;
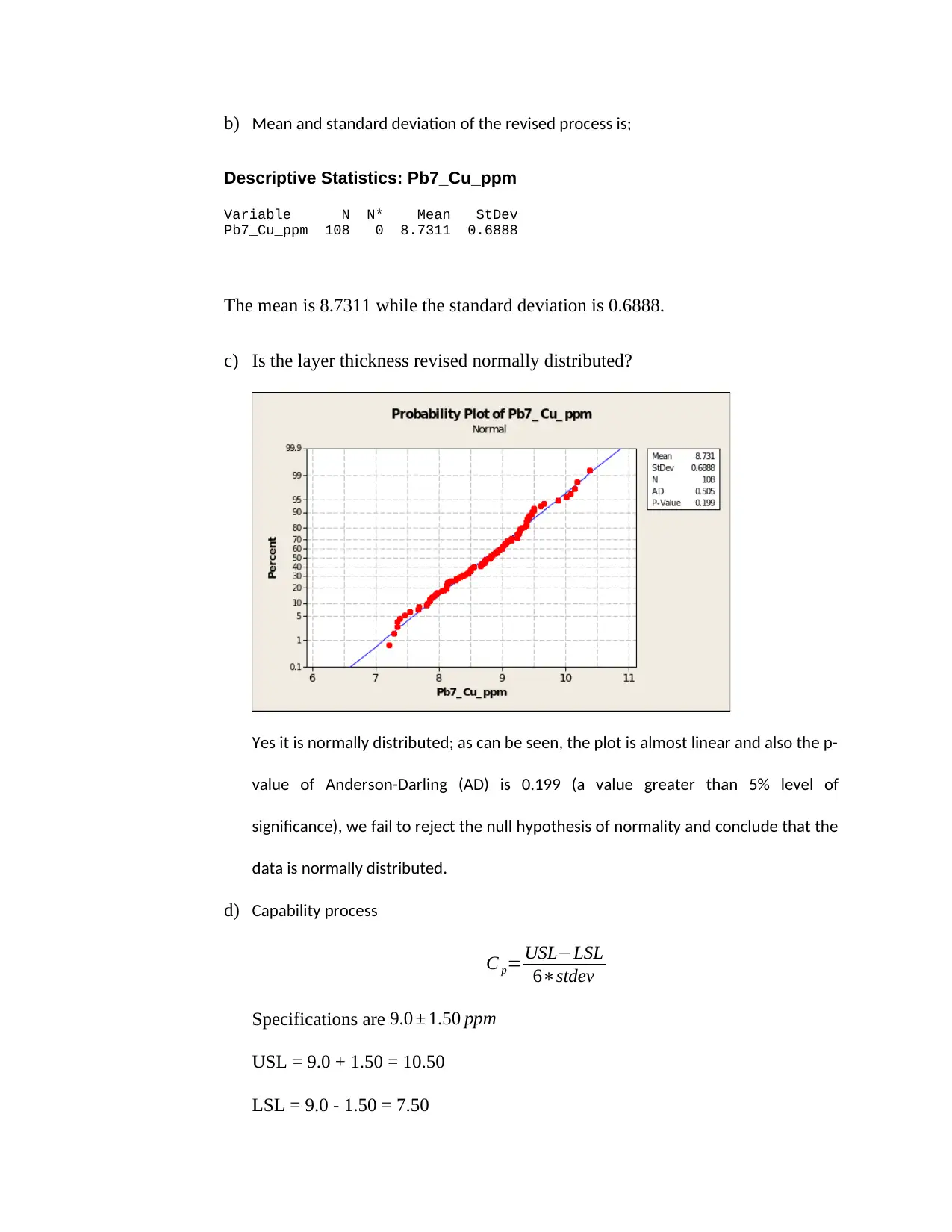
Descriptive Statistics: Pb7_Cu_ppm
Variable N N* Mean StDev
Pb7_Cu_ppm 108 0 8.7311 0.6888
The mean is 8.7311 while the standard deviation is 0.6888.
c) Is the layer thickness revised normally distributed?
Yes it is normally distributed; as can be seen, the plot is almost linear and also the p-
value of Anderson-Darling (AD) is 0.199 (a value greater than 5% level of
significance), we fail to reject the null hypothesis of normality and conclude that the
data is normally distributed.
d) Capability process
C p= USL−LSL
6∗stdev
Specifications are 9.0 ± 1.50 ppm
USL = 9.0 + 1.50 = 10.50
LSL = 9.0 - 1.50 = 7.50

C p= 10.5−7.5
6∗0.6888 =0.7259
Question 8:
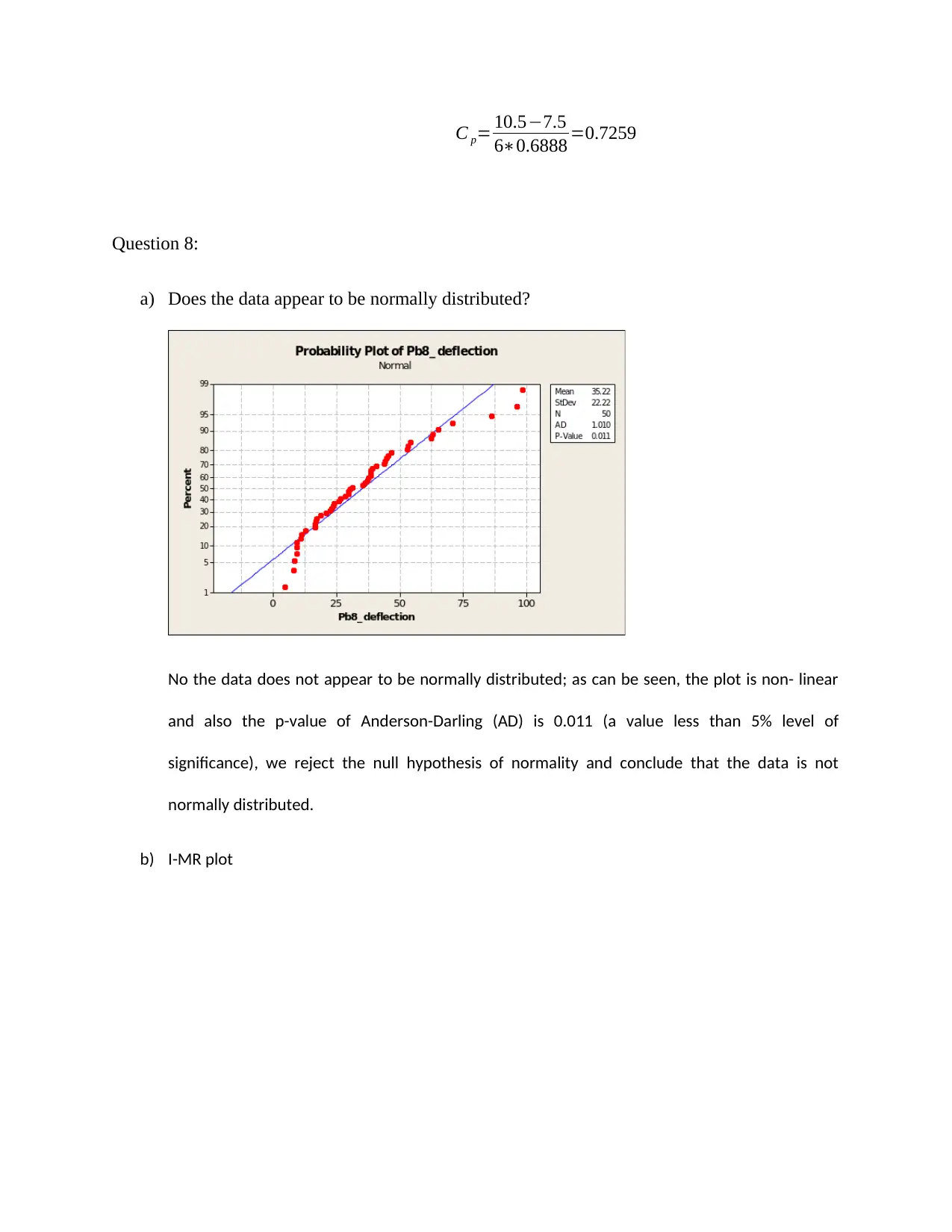
a) Does the data appear to be normally distributed?
No the data does not appear to be normally distributed; as can be seen, the plot is non- linear
and also the p-value of Anderson-Darling (AD) is 0.011 (a value less than 5% level of
significance), we reject the null hypothesis of normality and conclude that the data is not
normally distributed.
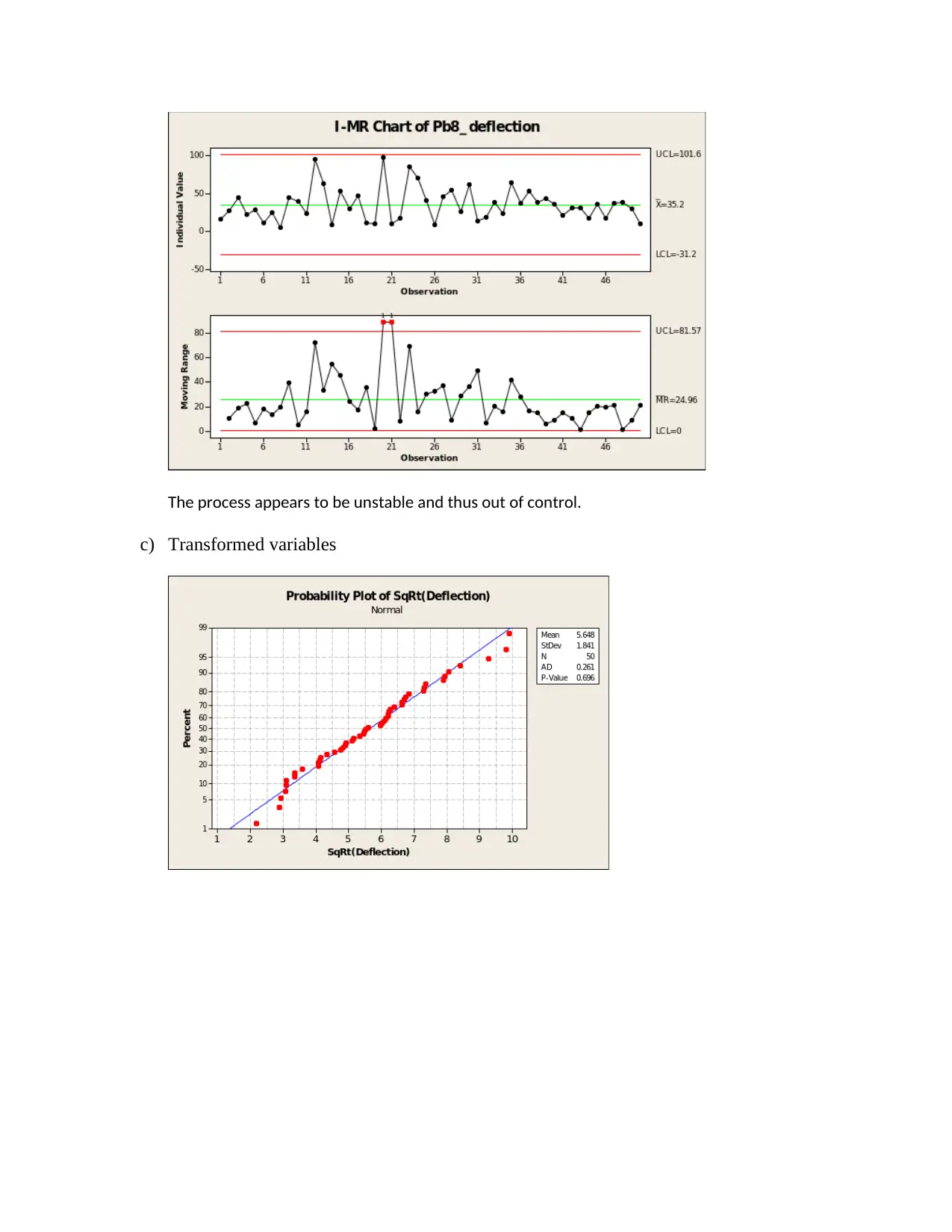
b) I-MR plot

The process appears to be unstable and thus out of control.
c) Transformed variables

As can be seen both the SqRt(deflection) and Ln(deflection) appear to be normally distributed.
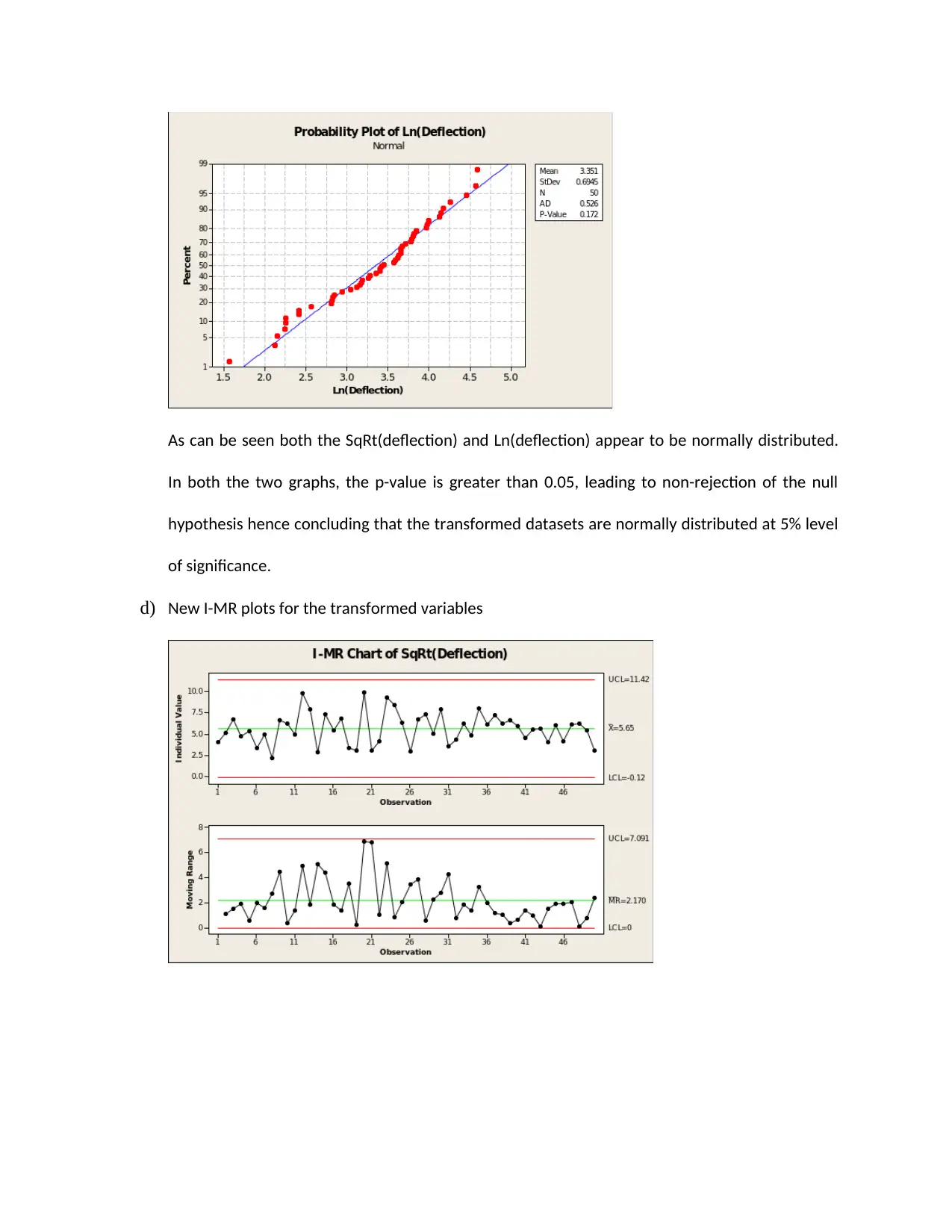
In both the two graphs, the p-value is greater than 0.05, leading to non-rejection of the null
hypothesis hence concluding that the transformed datasets are normally distributed at 5% level
of significance.
d) New I-MR plots for the transformed variables

The two transformed datasets now appear to be stable and as such are in control unlike the
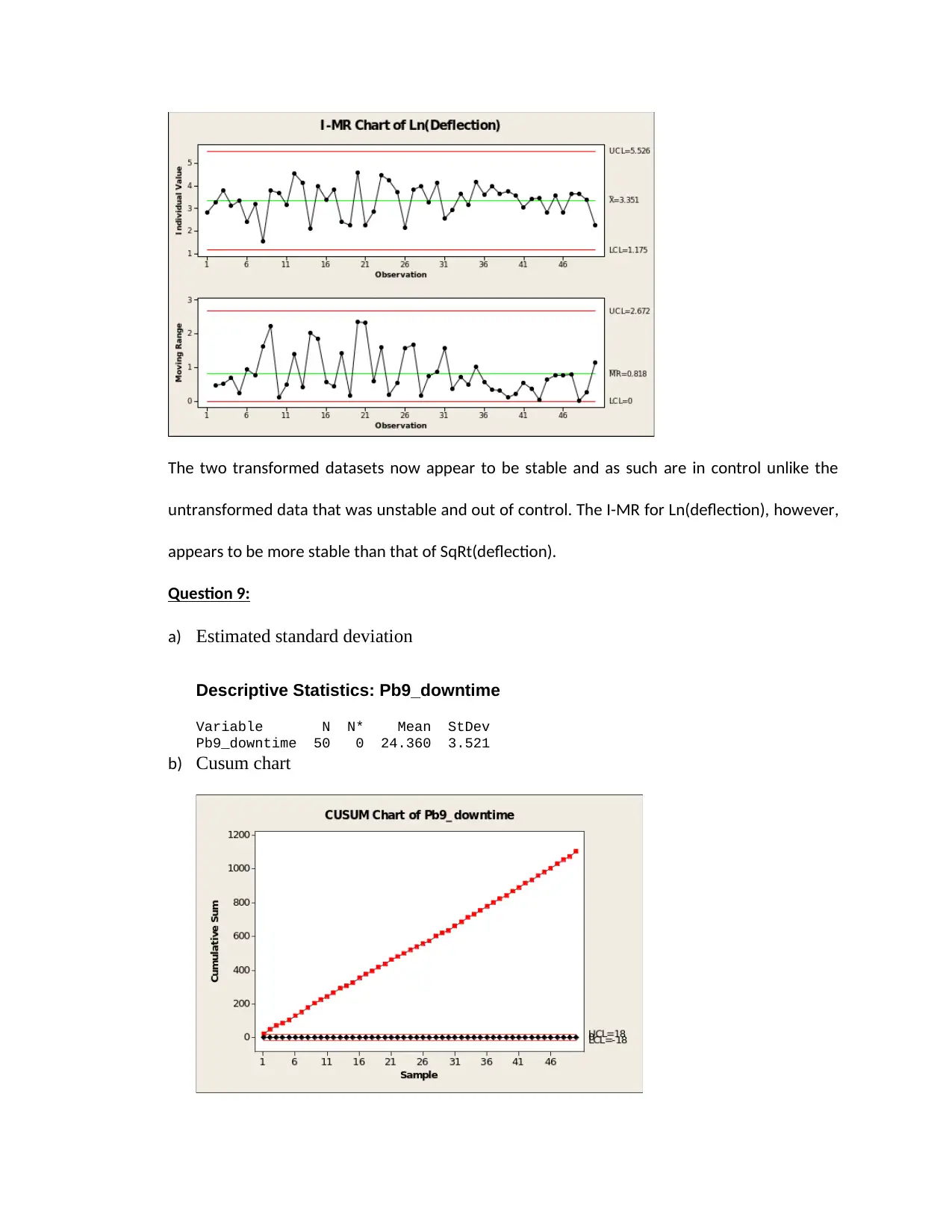
untransformed data that was unstable and out of control. The I-MR for Ln(deflection), however,
appears to be more stable than that of SqRt(deflection).
Question 9:
a) Estimated standard deviation
Descriptive Statistics: Pb9_downtime
Variable N N* Mean StDev
Pb9_downtime 50 0 24.360 3.521
b) Cusum chart

The plot shows that the process does not conform with the set standards.
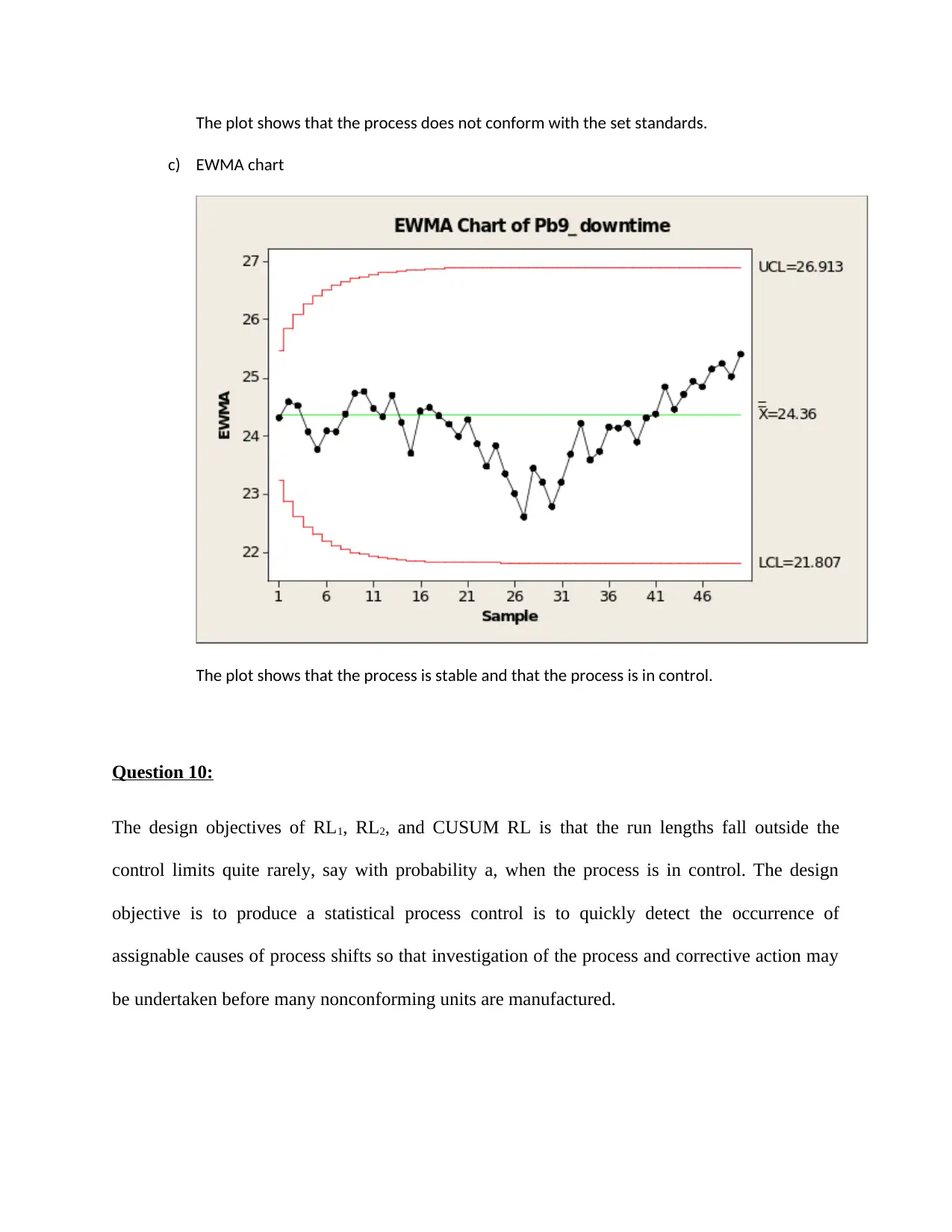
c) EWMA chart
The plot shows that the process is stable and that the process is in control.
Question 10:
The design objectives of RL1, RL2, and CUSUM RL is that the run lengths fall outside the
control limits quite rarely, say with probability a, when the process is in control. The design
objective is to produce a statistical process control is to quickly detect the occurrence of
assignable causes of process shifts so that investigation of the process and corrective action may
be undertaken before many nonconforming units are manufactured.

Some of the advantages of Run-Length (RL) charts is the fact that it gives a clear visualization of
the charts showing off the parameter for easy comprehension. However, it is limited by the fact
that it is complex and involves complex computations.