Quantitative Methods for Business Alternative Assessment 2020/21

This document provides study material for the Quantitative Methods for Business Alternative Assessment 2020/21. It includes questions and solutions related to mean, standard deviation, interpretation, sampling techniques, probability, correlation analysis, and more.

QUANTITATIVE METHODS FOR
BUSINESS ALTERNATIVE
ASSESSMENT 2020/21

TABLE OF CONTENTS
TABLE OF CONTENTS.................................................................................................................2
QUESTION 1...................................................................................................................................3
a........................................................................................................................................................3
I. Mean:........................................................................................................................................3
II. Standard Deviation:.................................................................................................................3
III. Interpretation:.........................................................................................................................3
b........................................................................................................................................................3
c........................................................................................................................................................4
Question 3........................................................................................................................................5
I....................................................................................................................................................5
II...................................................................................................................................................6
III.................................................................................................................................................6
b........................................................................................................................................................6
I....................................................................................................................................................6
II...................................................................................................................................................6
Question 4........................................................................................................................................7
a........................................................................................................................................................7
b........................................................................................................................................................7

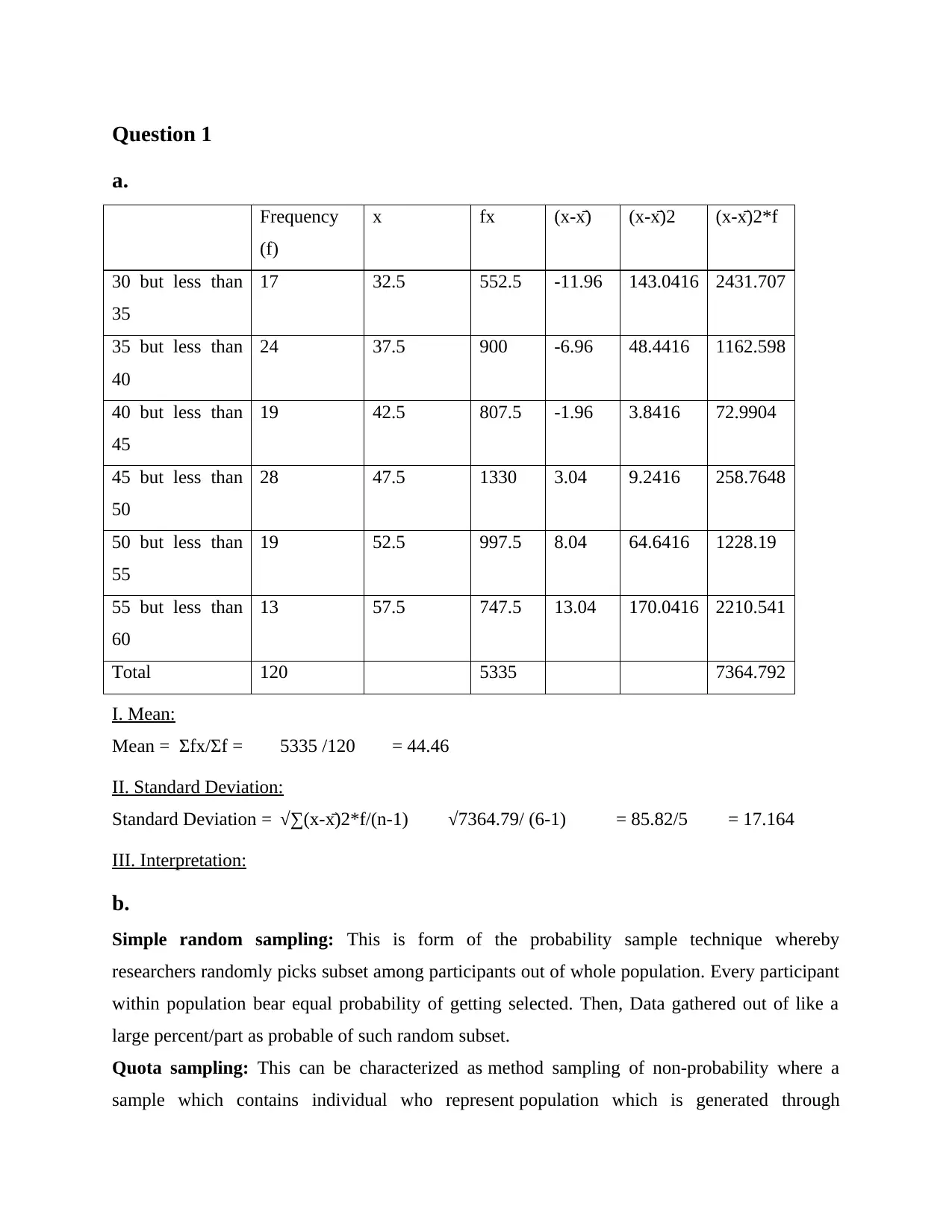
Question 1
a.
Frequency
(f)
x fx (x-x̄) (x-x̄)2 (x-x̄)2*f
30 but less than
35
17 32.5 552.5 -11.96 143.0416 2431.707
35 but less than
40
24 37.5 900 -6.96 48.4416 1162.598
40 but less than
45
19 42.5 807.5 -1.96 3.8416 72.9904
45 but less than
50
28 47.5 1330 3.04 9.2416 258.7648
50 but less than
55
19 52.5 997.5 8.04 64.6416 1228.19
55 but less than
60
13 57.5 747.5 13.04 170.0416 2210.541
Total 120 5335 7364.792
I. Mean:
Mean = Σfx/Σf = 5335 /120 = 44.46
II. Standard Deviation:
Standard Deviation = √∑(x-x̄)2*f/(n-1) √7364.79/ (6-1) = 85.82/5 = 17.164
III. Interpretation:
b.
Simple random sampling: This is form of the probability sample technique whereby
researchers randomly picks subset among participants out of whole population. Every participant
within population bear equal probability of getting selected. Then, Data gathered out of like a
large percent/part as probable of such random subset.
Quota sampling: This can be characterized as method sampling of non-probability where a
sample which contains individual who represent population which is generated through

researchers. As specific characteristics or attributes, researchers has chosen those people. This
find and establish number such that samples through market analysis could been important for
collection of data. The entire population could be generalised by such sampling.
Sampling frame: This implies database by which components for sample is taken. For
example, in the phone book telephone numbers would exist sampled, or whatever other concise
of population, Like such a diagram region would be sampled,listing' could be actual collection
of a unit. Where sampling frame isn't a reliable and full representation of entire population of
value, frame error occurs.
Cluster sampling: Under this technique researcher segregate population into different minor
groups regarded as clusters. Under it, they on random basis pick among such clusters in order to
make sample. This is technique of taking probability sample which is mainly employed to
analyse large population, especially those which are largely geographical basis dispersed.
Systematic sampling: This refers to a method of probability sampling which involves the
sample members which is from large population and are selected according to starting point
which is random but with fixed along with periodic interval. This interval known as
sampling interval which is calculated by population size which is divided by the
desired sample size.
c.
Numbers Frequency
3 2
7 1
8 1
9 1
11 1
12 1
13 2
15 1
16 1
17 2
18 1

19 2
20 2
21 2
22 6
23 5
24 5
25 2
26 3
27 2
28 3
29 1
30 1
31 1
33 1
Interval Frequency Cumulative
Frequency
1 to 10 5 5
11 to 20 13 18
21 to 30 30 48
31 to 40 2 50
Question 3
I.
 Charlie can solve the problem 1440/6= 240 times. He will NOT solve it 1440- 240= 1200
times.
 Of those 1200 times, Albert can solve it 1200/8= 150 times and NOT solve it 1200- 150=
1050 times.
 Of those 1050 times John can solve it 1050/3= 350 times and not solve it 1050- 350= 700
times.

 All three will not solve it 700/1440= 0.486 of time.
 The probability all three will NOT solve the problem is 0.486 or 48.6%.
II.
Charlie & Albert will not solve this problem but John WILL 350 times out of the 1440.
Charlie is not able to solve the problem but Albert will 150 times & of those 150 times John will
solve it 150/3= 50 times so will not solve it 100 times. That is, Charlie & John will not solve the
problem and Albert will 100 times out of 1440.
Charlie is able solve the problem 240 times. Of those 240 times Albert will solve it 240/8= 30
times and not solve it 240- 30= 210 times. Of those 210 times John will solve it 210/3= 70 and
not solve it 210- 70= 140 times. Charlie can solve the problem but Albert and John not solve it
140 times out of 1440 times.
That is, exactly one of the three will solve the problem a total of 350+ 100+ 140= 590 times out
of 1440. That is a probability of 590/1440= 0.410 or 41%.
III.
Based on above two scenario probability of only one of them solves the problem would be =
1440-590 = 850. Thus probability is 59%.
b.
I.
One is green and the other is white: 4C2 + 3C2 = (4 * 3)/2 + 3 * 2 = 6 + 6 = 12
Total Probability of two balls = 14C2 = (14 * 13) /2 = 91
Probability of One is green and the other is white: 12 / 91
II.
They are of same colour: 4C1 + 3C1 = 4 + 3 = 7
Total Probability of two balls = 14C2 = (14 * 13) /2 = 91
Probability of same colour: 7 / 91

Question 4
a.
Brand Price/Litre
Ranking
Quality
ranking
d d2
T 1.92 2 -0.08 0.0064
U 1.58 6 -4.42 19.5364
V 1.35 7 -5.65 31.9225
W 1.6 4 -2.4 5.76
X 2.05 3 -0.95 0.9025
Y 1.39 5 -3.61 13.0321
Z 1.77 1 0.77 0.5929
71.7528
p = 1 – (6 * 71.52)/ [7 * (49-1)] = 430.52 / 336 = 1.2813
Analysis: Spearman correlation coefficient as computed above is +1 which indicates perfect
association among ranks. This implies that consumer gets value for their monies.
b.

Employees X Y x-x̄ y-ȳ (x-x̄)
(y- ȳ)
(x-x̄)2 (y- ȳ)2
A 4 21 -5 5 -25 25 25
B 5 22 -4 6 -24 16 36
C 7 15 -2 -1 2 4 1
D 9 18 0 2 0 0 4
E 10 14 1 -2 -2 1 4
F 11 14 2 -2 -4 4 4
G 12 11 3 -5 -15 9 25
H 14 13 5 -3 -15 25 9
72 128 -83 84 108
x̄ = 9
ȳ = 16
r = -83 / √ (84*108) = -83/95.25 = -0.87142
Analysis: There is negative correlation in data given i.e. -0.87 which shows that there is perfect
negative correlation among weeks of experience and number of rejects of different employees.

REFERENCES
Bhardwaj, 2016. Predictability and wavelet analysis of air pollutants for commercial and
industrial regions in Delhi. Indian Journal of Industrial and Applied Mathematics, 7(2),
pp.165-174.
Wang, 2018. Uncertain rank correlation analysis based on normal interval value. Journal of
Intelligent & Fuzzy Systems, 35(1), pp.69-74.
Karaca, 2017. Rank determination of mental functions by 1D wavelets and partial
correlation. Journal of medical systems, 41(1), pp.1-10.
XIAO, 2018. Dynamic Interval Scales Rank Correlation Analysis Group Evaluation Method and
its Application. Journal of Chongqing University of Technology (Natural Science),
p.05.
Deustua, 2018. Communication: Approaching exact quantum chemistry by cluster analysis of full
configuration interaction quantum Monte Carlo wave functions. The Journal of
chemical physics, 149(15), p.151101.
Escamilla-Guerrero, 2020. Revisiting Mexican migration in the Age of Mass Migration: New
evidence from individual border crossings. Historical Methods: A Journal of
Quantitative and Interdisciplinary History, 53(4), pp.207-225.