Comprehensive Statistics Assignment: Data Analysis and Probability
VerifiedAdded on 2023/04/22
|15
|1444
|214
Homework Assignment
AI Summary
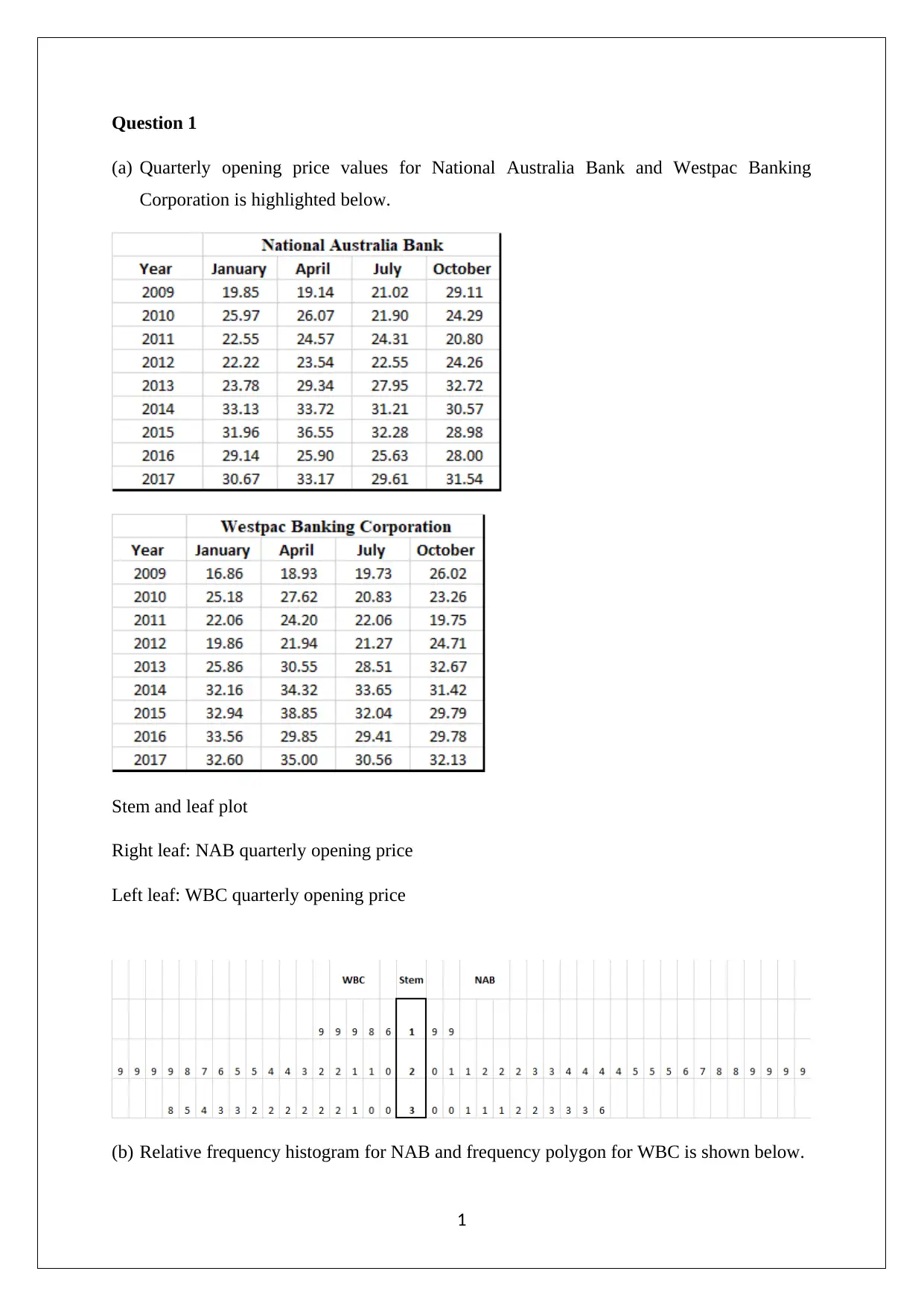
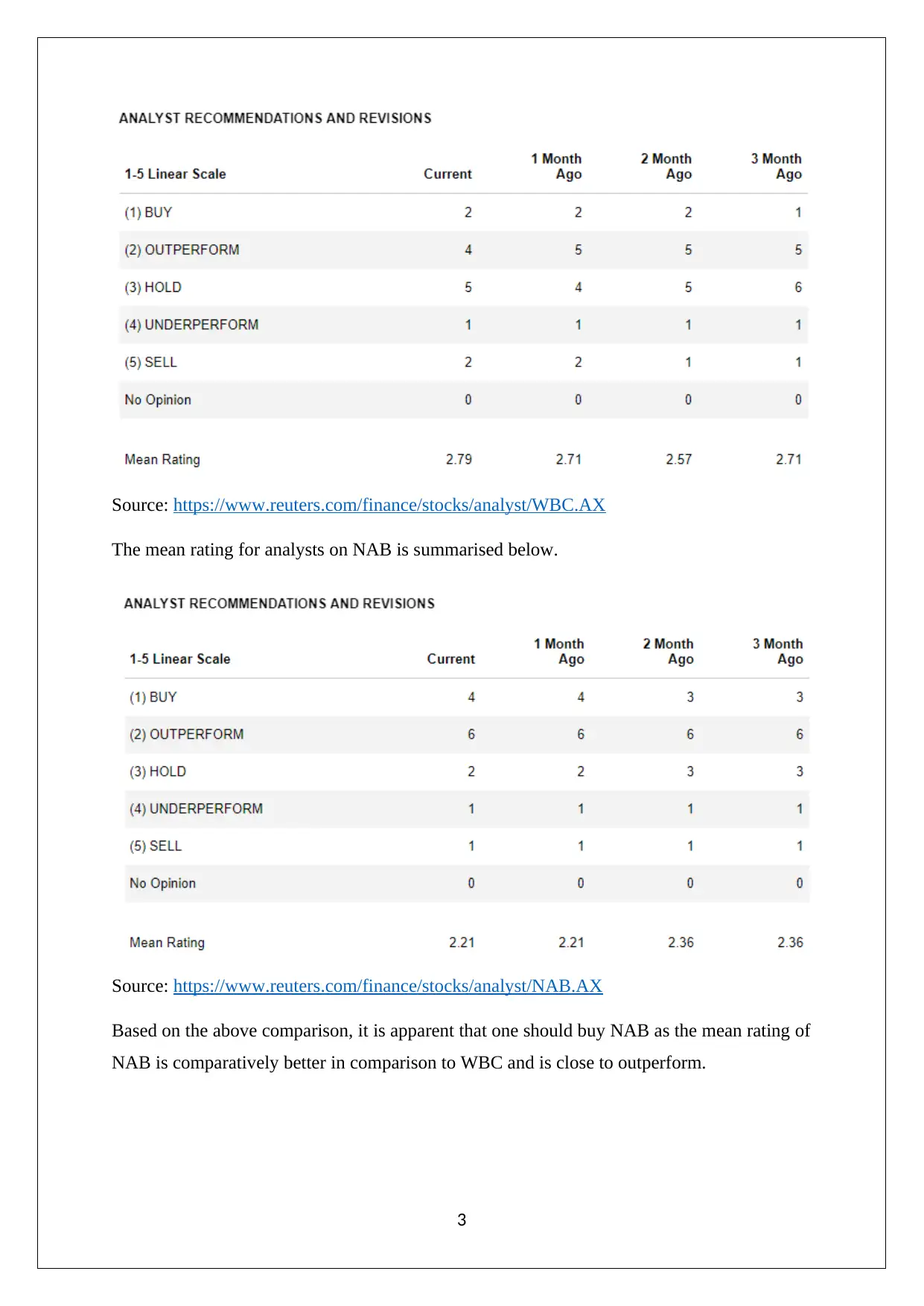
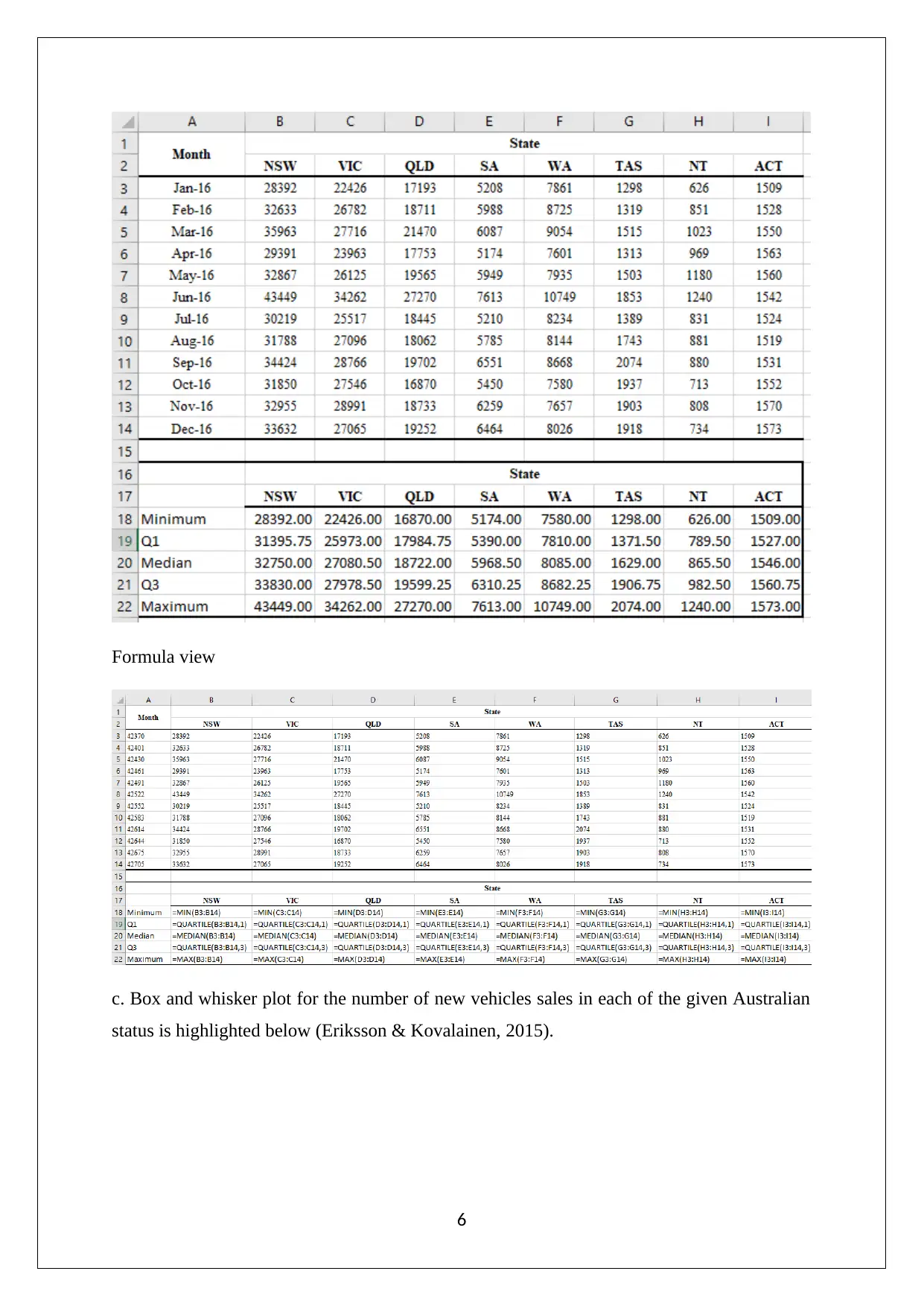
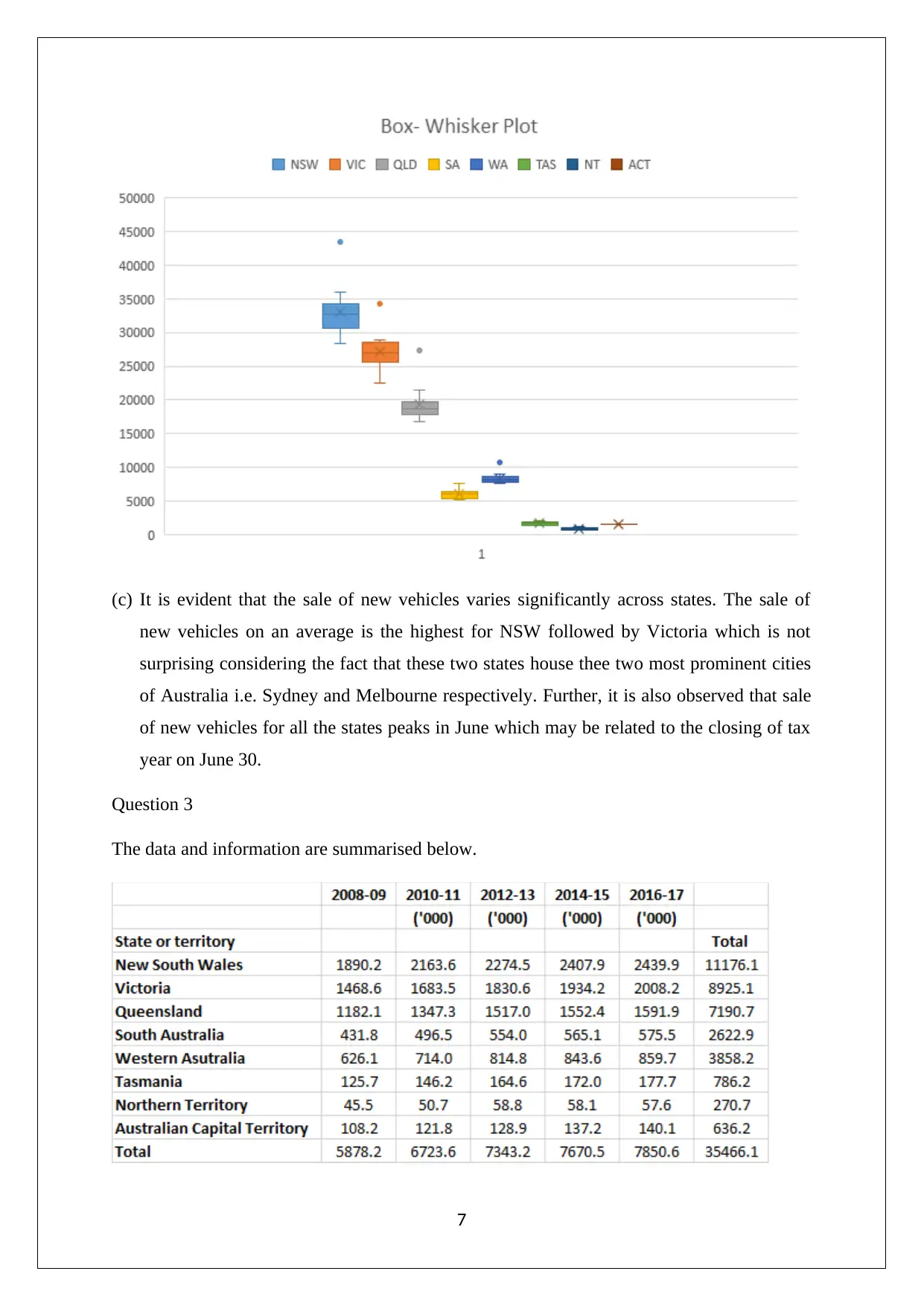
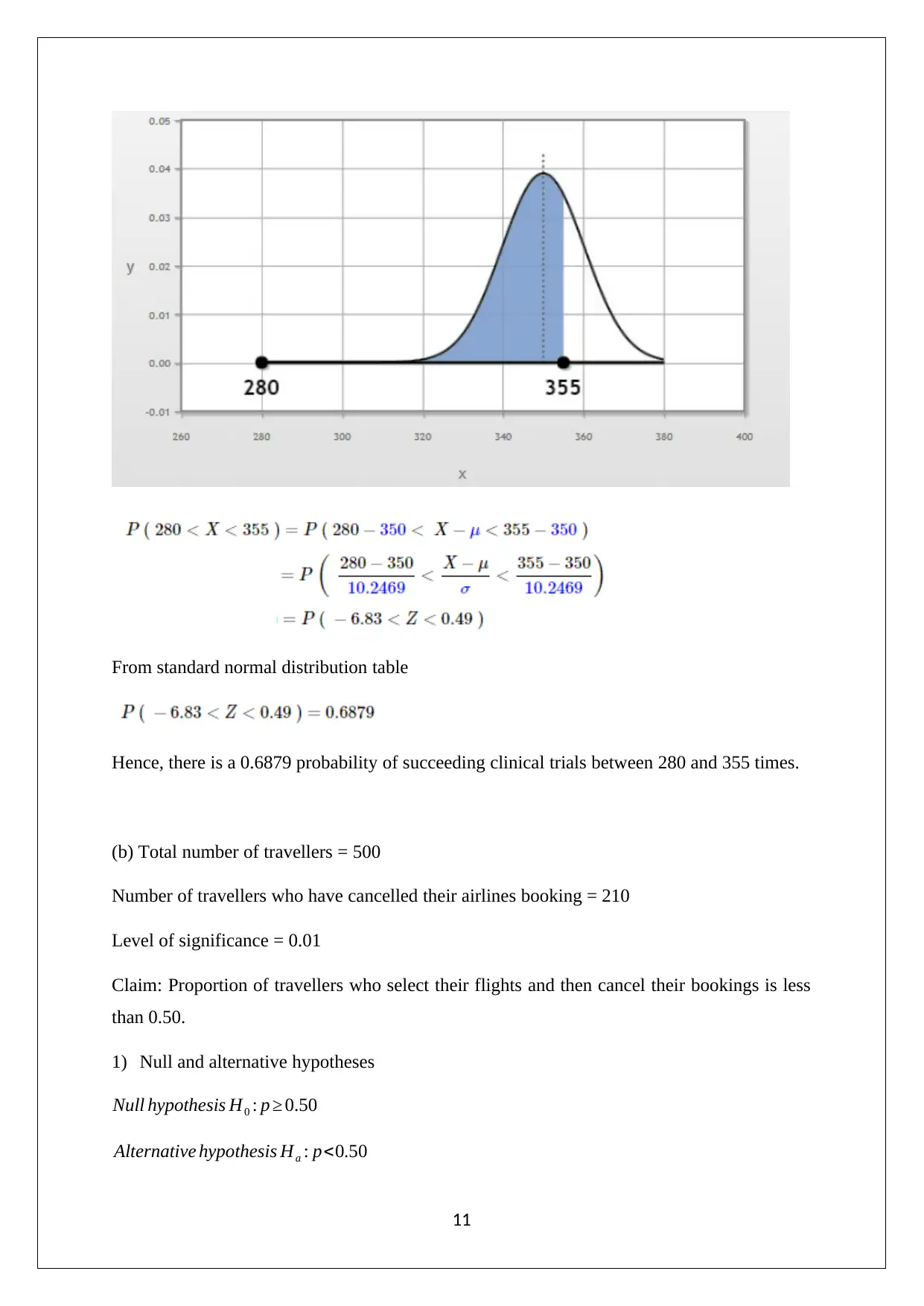
This statistics assignment solution covers a range of topics including descriptive statistics, probability, hypothesis testing, and confidence intervals. The first question involves analyzing quarterly opening prices for National Australia Bank (NAB) and Westpac Banking Corporation (WBC) using stem and leaf plots, relative frequency histograms, and bar graphs, concluding with a recommendation to buy NAB based on analyst ratings. Question 2 focuses on computing mean, standard deviation, minimum, quartiles, and maximum values for new vehicle sales across Australian states, visualized with box and whisker plots. Question 3 calculates various probabilities related to household demographics and internet access. Question 4 addresses normal and uniform distributions, including calculating probabilities and z-values. Finally, Question 5 covers binomial distribution approximation, hypothesis testing for proportions, and confidence interval estimation. This solved assignment is available on Desklib, a platform offering a wide range of study resources for students.
1 out of 15














![[object Object]](/_next/static/media/star-bottom.7253800d.svg)