University FEA Assignment: Contact Analysis and Elliptical Constraints
VerifiedAdded on 2022/08/23
|4
|555
|22
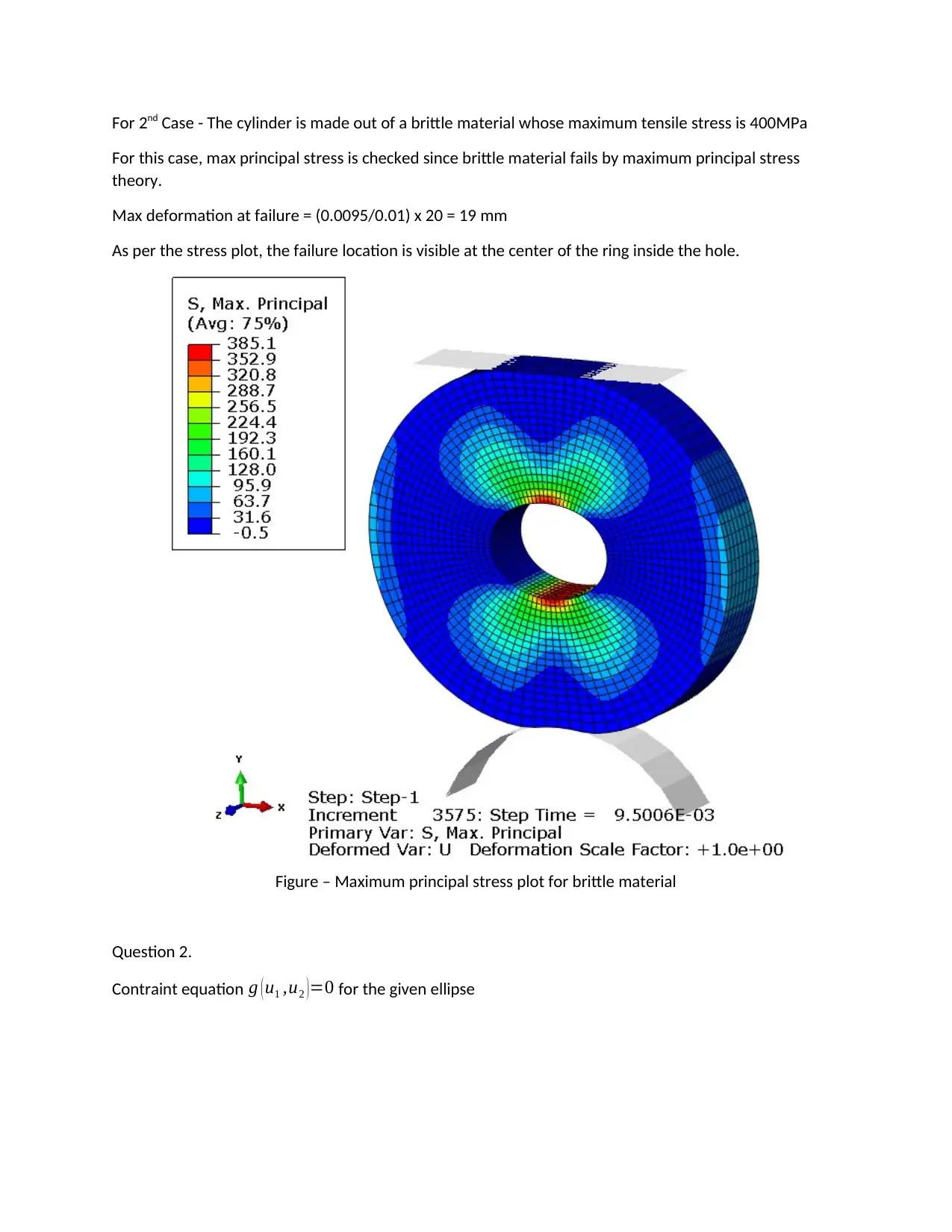
Homework Assignment
AI Summary
This document presents a detailed solution to a Finite Element Analysis (FEA) assignment. The first part of the solution focuses on contact analysis using ABAQUS, simulating a hollow cylinder subjected to compressive forces from rigid indenters. The solution explores two cases: one where the cylinder material fails based on von Mises stress and another where failure is determined by maximum tensile stress, providing calculated deformation values at failure and failure locations. The second part of the solution addresses an elliptical constraint problem, deriving the constraint equation and solving it using both the penalty method and Lagrange multipliers method. The solution includes the mathematical derivations, the constraint equations, and the Mathematica code used to solve the problem. The document provides a comprehensive understanding of the problem, the methods used to solve it, and the results obtained.
1 out of 4





![[object Object]](/_next/static/media/star-bottom.7253800d.svg)