Question 2 When X = $40, European Call Options Price When X = $40

Question 2 Where Where Hence, .3413 X = $40; European call options price For X = $45 European call options price X = $50 European call options price When X = $40, Putting back into the formula When X = $45, C = $2.40 (Serirungsun, 2013) Putting back into the formula When X = $50, C = $0.70 All the value of t is maximum when X is equal to . When X = $40, When X = $45 When

Question 1
Given
r =0.045
σ =0.24
T = 1
4
S0 =$ 45
d St =St ( rdt +σd Bt ) …………………..(i)
Where Bt N ( 0 ,t ) 0 ≤t ≤T … …..…………………..(ii)
Expanding;
St i
−Sti−1
=St i−1
( r ∆ t+ σϵ √∆ t ) ……………………………(iii)
Where ∆ t=ti−t i−1. We will apply an interval of 0.005 that is ∆ t=0.005
ϵ N (0 , 1)
Thus, ϵ=0.3413
St i
=Sti−1
( r ∆t +0.3413 √∆ t ) +Sti−1
The simulation is represented in excel attached.
Question 2
d St =St ( rdt + σd Bt )
Where Bt N ( 0 ,t ) 0 ≤t ≤T
St i
−Sti−1
=St i−1
( r ∆ t+ σϵ √∆ t )
Where ∆ t=ti−t i−1=0.005
ϵ N (0 , 1)

Hence, ϵ=0.3413
St i
=Sti−1
( r ∆t +0.3413 √∆ t ) +Sti−1
S0 =45 ( 0.045∗0.25+0.3143 √0.25 ) +45=49.56
1) X = $40;
European call options price ¿ $ 5.81
For X = $45
European call options price ¿ 49.56−45
0.25 =$ 2.40
X = $50
European call options price ¿ 49.56−50
0.25−0.275 =$ 0.70
2) C=S0 N ( d1 )−X e−rt N ( d2 )
d1=
ln ( S0
X )+ (r + σ 2
2 )T
σ √T
d2=d1−σ √ T
When X = $40,
d1=1.1353
d2=1.0153
N ( d1 )=N ( 1.1353 ) =0.8719
N ( d2 )=N ( 1.0153 ) =0.8450
Putting back into the formula
5.81= ( 45∗0.8719 )− ( 40 e−0.045t∗0.8450 )
t=0.2476
When X = $45, C = $2.40
d1=0.1538 CITATION Pan13 \l 2057 (Serirungsun, 2013)
d2=0.0338
N ( d1 )=0.5611

N ( d2 )=0.5135
Putting back into the formula
2.40= ( 45∗0.5611 ) − ( 45∗e−0.045t∗0.5135 )
t=6.497
When X = $50, C = $0.70
d1=−0.7243
d2=−0.8443
N ( d1 )=0.2345
N ( d2 ) =0.1993
0.70= ( 45∗0.2345 )− ( 50∗0.1993∗e−0.045 t )
t=0.2523
All the value of t is maximum when X is equal to S0.
3) When X = $40,
P=$ 0.36
When X = $45
P=$ 1.90
When X = $50,
P=$ 5.14
4) When X = $40, C= $38.24
P = C−S0 + X e−rT
P=5.81−45+ 40 e−0.045∗0.25=−$ 40.41
When X = $45, C = $2.40
P=2.40−45+ 45 e−0.045∗0.25=−$ 43.98
When X = $50, C = $0.70
P=0.70−45+50 e−0.045∗0.25=−$ 45.83
Question3

1. u=exp ( 0.24∗ √ 0.25
100 ) =1.012
d= 1
1.012 =0.988
2. R=(1+ r
n )T
=(1+ 0.045
100 )0.25
=1.0001
3. q= R−d
u−d = 1.0001−0.988
1.012−0.988 =0.50 CITATION Mar12 \l 2057 (Marek Capinski, 2012)
4. q' =uq
R =1.012∗0.5
1.0001 =0.506
5. a=
ln( S0
X )+n ln d
ln ( d
u )
When X = $40
a=
ln ( 45
40 )+100 ln(0.988)
ln ( 0.988
1.012 ) =45.39
When X = $45
a=
ln ( 45
45 )+ 100 ln (0.988)
ln ( 0.988
1.012 ) =49.90
When X = $50
a=
ln ( 45
50 )+ 100 ln(0.988)
ln ( 0.988
1.012 ) =54.69
6. When X = $40,
P [ J ≥ 45.39 ]=0.174 , P [ J' ≥ 45.39 ]=1−0.174=0.826
When X = $45,
P [ J ≥ 49.90 ]=0.192 , P [ J ' ≥ 49.90 ]=0.808

When X = $50,
P [ J ≥ 54.69 ] =0.194 , P [ J ' ≥ 44.98 ] =1−0.194=0.806
7. When X =$40
C0= ( 45∗0.826 ) − ( 40∗1.0001−100∗0.174 ) =$ 30.21
When X = $45
C0= ( 45∗0.808 ) − ( 45∗1.0001−100∗0.192 ) =$ 27.72
For X = $50
C0= ( 45∗0.806 ) − ( 50∗1.0001−100∗0.194 ) =$ 26.57
The amounts obtained here exceed those gotten using Black Scholes Merton Prices
method.
Question 4
From the calculations above, all the three methods are dependent on each other. This means that
they use related quantities in computation. Both values made use of r, T, S(0) and σ . However,
the application of this variables differ and thus the results obtain differ by a large margin.
However, there methodology is varying. From the results, we obtain that the put-call clarity
method resulted to values lower than those of Black Scholes Morten prices. The put values were
higher than those of call option.
Question 5
Part A
C0=S0 P [ J' ≥ a ] − X R−n P [ J ≥ a ]
R=(1+ r
n )T
=(1+ 0.045
6 )0.25
=1.002
Let P [ J ≥ a ]= y , thus P [ J' ≥ a ]=1− y
Therefore, C0=S0 (1− y)−X R−n y

For X = 40,
30.21=45 ( 1− y )−(40∗1.002−6∗y)
Solving for y we get
y=0.175
Thus, P [ J ≥ a ]=0.175
a=45.40
a=
ln ( S0
X )+nln d
ln ( d
u ) =
ln ( 45
40 )+6 ln ( 1
u )
ln ( 1
u2 ) =45.40
Solving for u we get
u=0.999
But u=exp (σ √ T
n )
0.999=eσ √ 0.25
6
Solving for σ we obtain
σ =−0.0049
This value will serve all the strikes.
The volatility smile is -0.0049 (see the attached excel).
Part B
The volatility smile shows the change in implied volatility related to the percentage change in
moneyness. For the obtained negative value, it indicates that for a decrease in moneyness, there
is a volatility decrease of 0.49%. In simple terms, when the value of money depreciates, less

products are purchased. The results of this is decrease in price as compared to the inflation rates.
This model is relatively similar to Black Scholes Morten methodology which results in a
decrease in option price as strike price increase. This creates an inversely proportional
relationship between option price and strike price. BMS assumes that volatility and risk free rate
of return is constant throughout the duration. This is not the ideal case in the real world. It is
corrected by keeping a keen look at the fluctuations.
BSM also ignores brokerage charges. The stop-gap measure is to buy when volatility is at a
lower range.
Question 6
Part A
P=C−S0+ X e−rT
But C=S0 N ( d1 )−X e−rt N ( d2 ) (Hoberg, 2009)
Substituting back we get
P0=S0 N ( d1 ) −X e−rt N ( d2 ) −S0 + X e−rT
Collecting like terms;
P0= X e−rt
( −N ( d2 ) +er ( T −r )
) −S0 ( 1+N ( d1 ) )
¿ X e−rT N (−d2 )−S0 N (−d1 )
Part B
For X = $40,
~
Puu=max { X−uu S0 , 0 } =max { 40−1.152∗45 , 0 }=0
~
Pud=max { X−ud S0 ,0 }=max { 40−1.15∗0.85∗45 , 0 } =0

~
Pdd=max { X−dd S0 }=max {40−0.852∗45 ,0 }=7.49
~
Pu=max { X−u S0 , 0 }=max {40−1.15∗45 , 0 }=0
~
Pd=max {X −d S0 , 0 }=max {40−0.85∗45 , 0 }=1.75
For X = $45
~
Puu=max { X−uu S0 , 0 } =max { 45−1.152∗45 , 0 }=0
~
Pud=max { X−ud S0 ,0 }=max { 45−1.15∗0.85∗45 , 0 } =1.01
~
Pdd=max { X−dd S0 }=max {45−0.852∗45 ,0 }=12.49
~
Pu=max { X−u S0 , 0 }=max {45−1.15∗45 , 0 }=0
~
Pd=max {X −d S0 , 0 }=max {45−0.85∗45 , 0 }=6.75
For X = $50
~
Puu=max { X−uu S0 , 0 }=max {50−1.152∗45 ,0 }=0
~
Pud=max { X−ud S0 ,0 }=max {50−1.15∗0.85∗45 ,0 }=6.01
~
Pdd=max { X−dd S0 }=max {50−0.852∗45 , 0 }=17.49
~
Pu=max { X−u S0 , 0 }=max {50−1.15∗45 ,0 }=0
~
Pd=max {X −d S0 , 0 }=max {50−0.85∗45 , 0 }=11.75
Question 7
Part A
Buying of puts provides an allowance for selling at strike price whereas long calls gives an
allowance for buying at a strike price.
There is an increase in value for calls when interest rates increase whereas for puts there is a
decrease in value. They also behave differently when the underlying price shifts. For example,

calls possess a positive delta insinuating that there is an increase in value as the stock price
shoots. Contrarily, puts have a negative delta thus decreases in value when the stock price
upsurge. The investor has to choose the most appropriate one to maximize profits (Korinek,
2009).
A protective put is a risk-management approach by means of options contracts that stockholders
hire to protect against the loss of possessing a stock or asset. The equivocation strategy
encompasses an investor purchasing a put option for a fee, called a premium.
Part B
1. u=exp ( 0.24∗ √ 0.25
100 ) =1.012
d= 1
1.012 =0.988
2. R=(1+ r
n )T
=(1+ 0.045
100 )0.25
=1.0001
3. q= R−d
u−d = 1.0001−0.988
1.012−0.988 =0.50 CITATION Mar12 \l 2057 (Marek Capinski, 2012)
4. q' =uq
R =1.012∗0.5
1.0001 =0.506
5. a=
ln( S0
X )+n ln d
ln ( d
u )
When X = $40
a=
ln ( 45
40 )+100 ln(0.988)
ln ( 0.988
1.012 ) =45.39
When X = $45
a=
ln ( 45
45 )+ 100 ln (0.988)
ln ( 0.988
1.012 ) =49.90
When X = $50

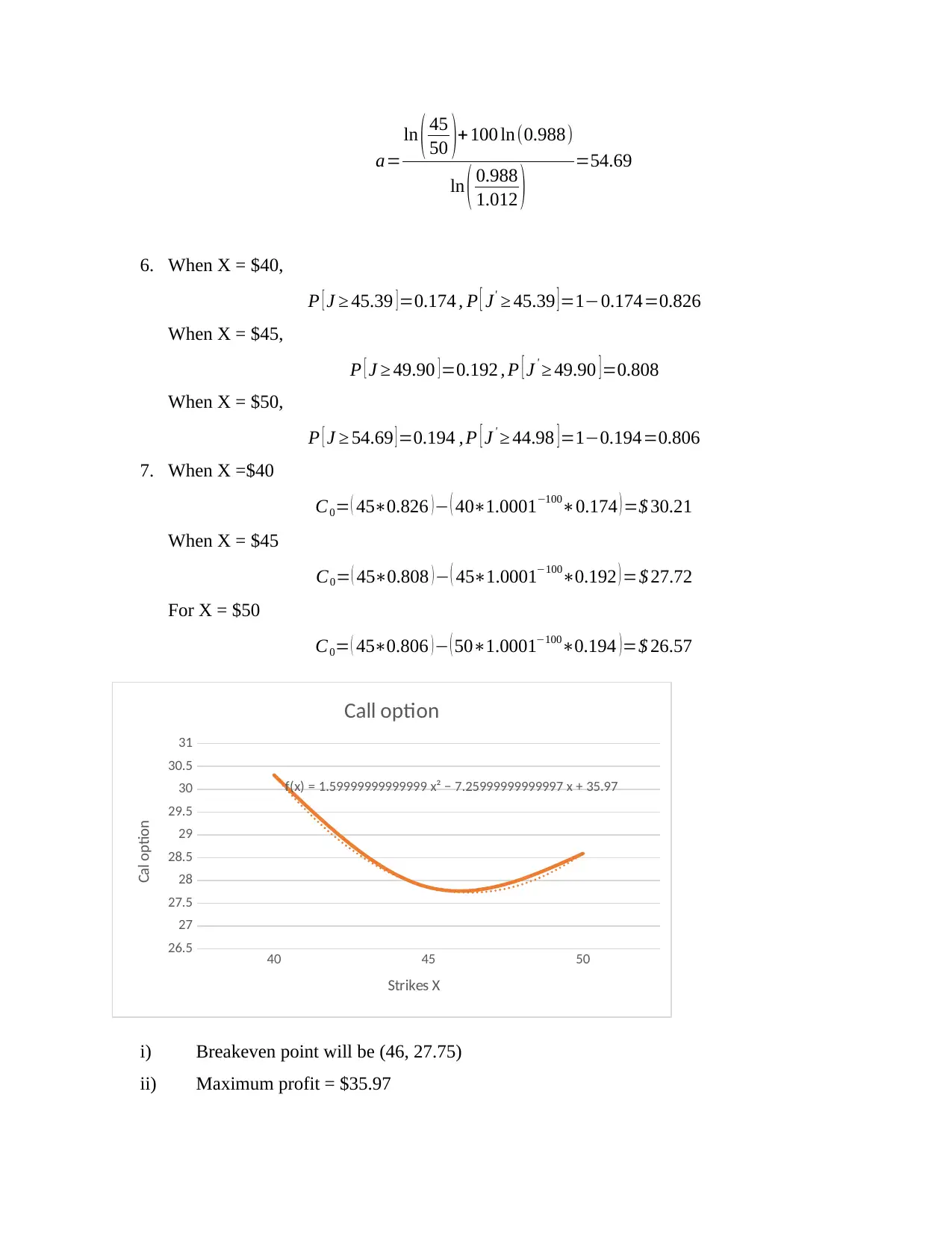
a=
ln ( 45
50 )+ 100 ln(0.988)
ln ( 0.988
1.012 ) =54.69
6. When X = $40,
P [ J ≥ 45.39 ]=0.174 , P [ J' ≥ 45.39 ]=1−0.174=0.826
When X = $45,
P [ J ≥ 49.90 ]=0.192 , P [ J ' ≥ 49.90 ]=0.808
When X = $50,
P [ J ≥ 54.69 ] =0.194 , P [ J ' ≥ 44.98 ] =1−0.194=0.806
7. When X =$40
C0= ( 45∗0.826 ) − ( 40∗1.0001−100∗0.174 ) =$ 30.21
When X = $45
C0= ( 45∗0.808 ) − ( 45∗1.0001−100∗0.192 ) =$ 27.72
For X = $50
C0= ( 45∗0.806 ) − ( 50∗1.0001−100∗0.194 ) =$ 26.57
40 45 50
26.5
27
27.5
28
28.5
29
29.5
30
30.5
31
f(x) = 1.59999999999999 x² − 7.25999999999997 x + 35.97
Call option
Strikes X
Cal option
i) Breakeven point will be (46, 27.75)
ii) Maximum profit = $35.97

iii) Minimum loss = $27.75
It is a call option. This is effective for future investment. Thus the investor must be one who has
long time plans and not quick ones. The future prices are estimated to rise.
References
Bielecki, T.R. and Rutkowski, M., 2013. Credit risk: modeling, valuation and hedging. Springer
Science & Business Media, pp. 76.
Hoberg, G. and Prabhala, N.R., 2009. Dividend policy, risk, and catering. Review of Financial
Studies, 22(1), pp.79-116.
Korinek, A. and Stiglitz, J.E., 2009. Dividend taxation and intertemporal tax arbitrage. Journal
of Public Economics, 93(1-2), pp.142-159.