University Project: Analysis of AC Machines Vector Control Methods
VerifiedAdded on 2023/03/30
|5
|912
|129
Project
AI Summary
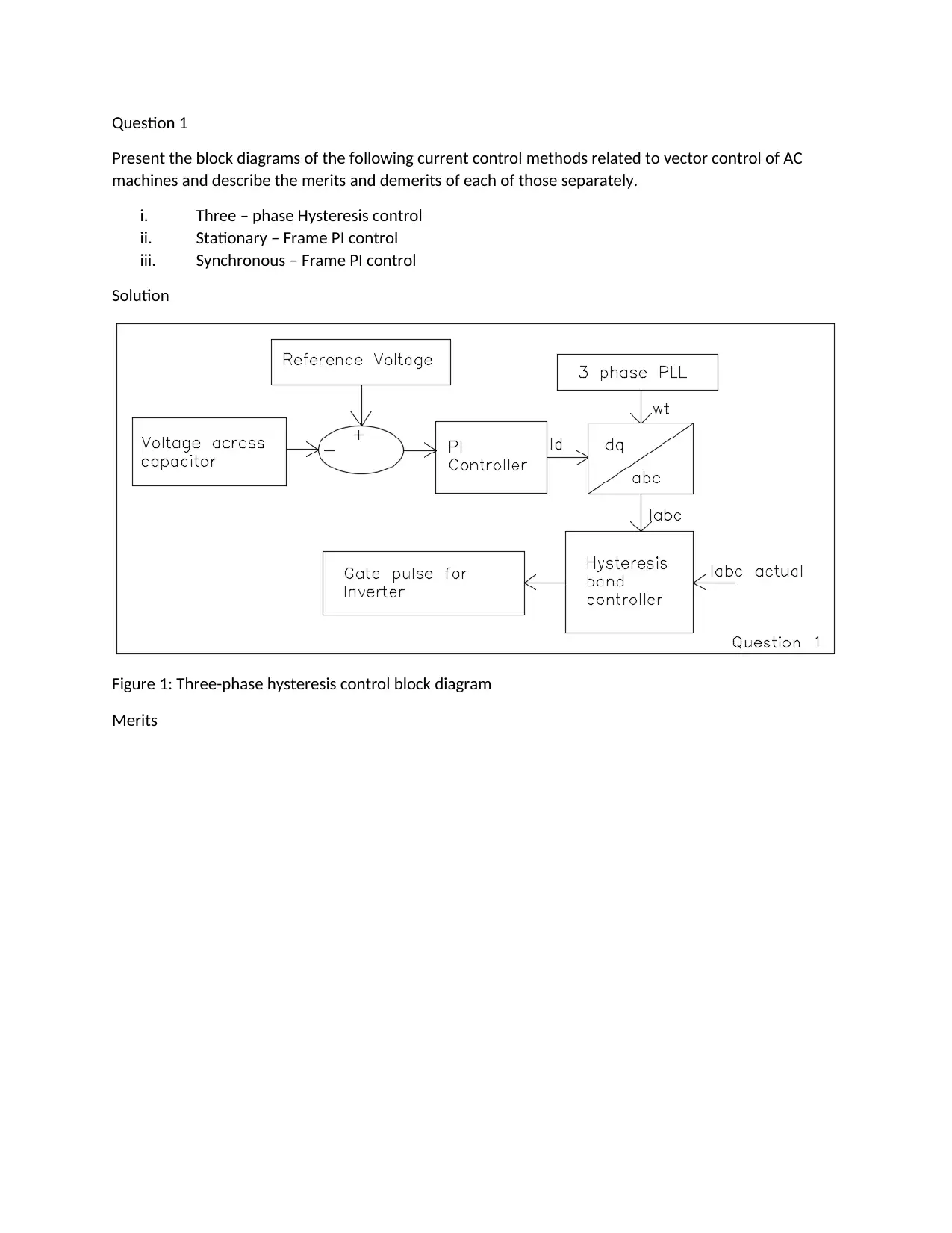
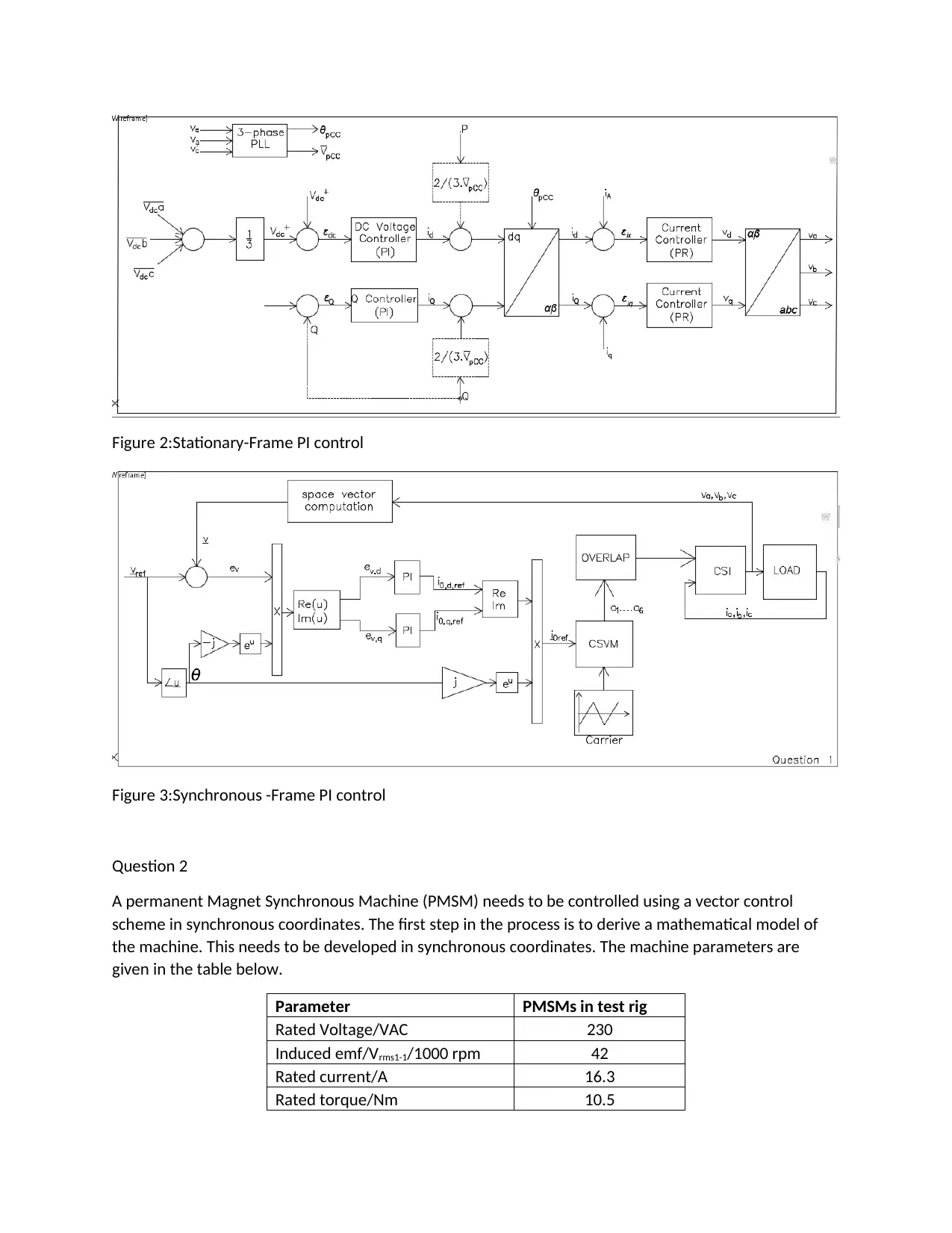
This project analyzes various vector control methods for AC machines, including three-phase hysteresis control, stationary-frame PI control, and synchronous-frame PI control, presenting their block diagrams, merits, and demerits. It then delves into the mathematical modeling of a Permanent Magnet Synchronous Machine (PMSM) in synchronous coordinates, deriving per-unit parameters based on given machine specifications. The solution includes detailed calculations for base values, per-unit values, and the dynamic model of the PMSM in a synchronous (dq) frame. Furthermore, the project covers the electromagnetic torque equation and provides block diagrams for the dynamic model, along with discussions on decoupling, Simulink implementation, internal model approach, and closed-loop speed control. Finally, it includes a Simulink model demonstration.
1 out of 5






![[object Object]](/_next/static/media/star-bottom.7253800d.svg)