Probability Problems: Expected Value, Distributions, and Testing
VerifiedAdded on 2023/04/08
|6
|679
|180
Homework Assignment
AI Summary
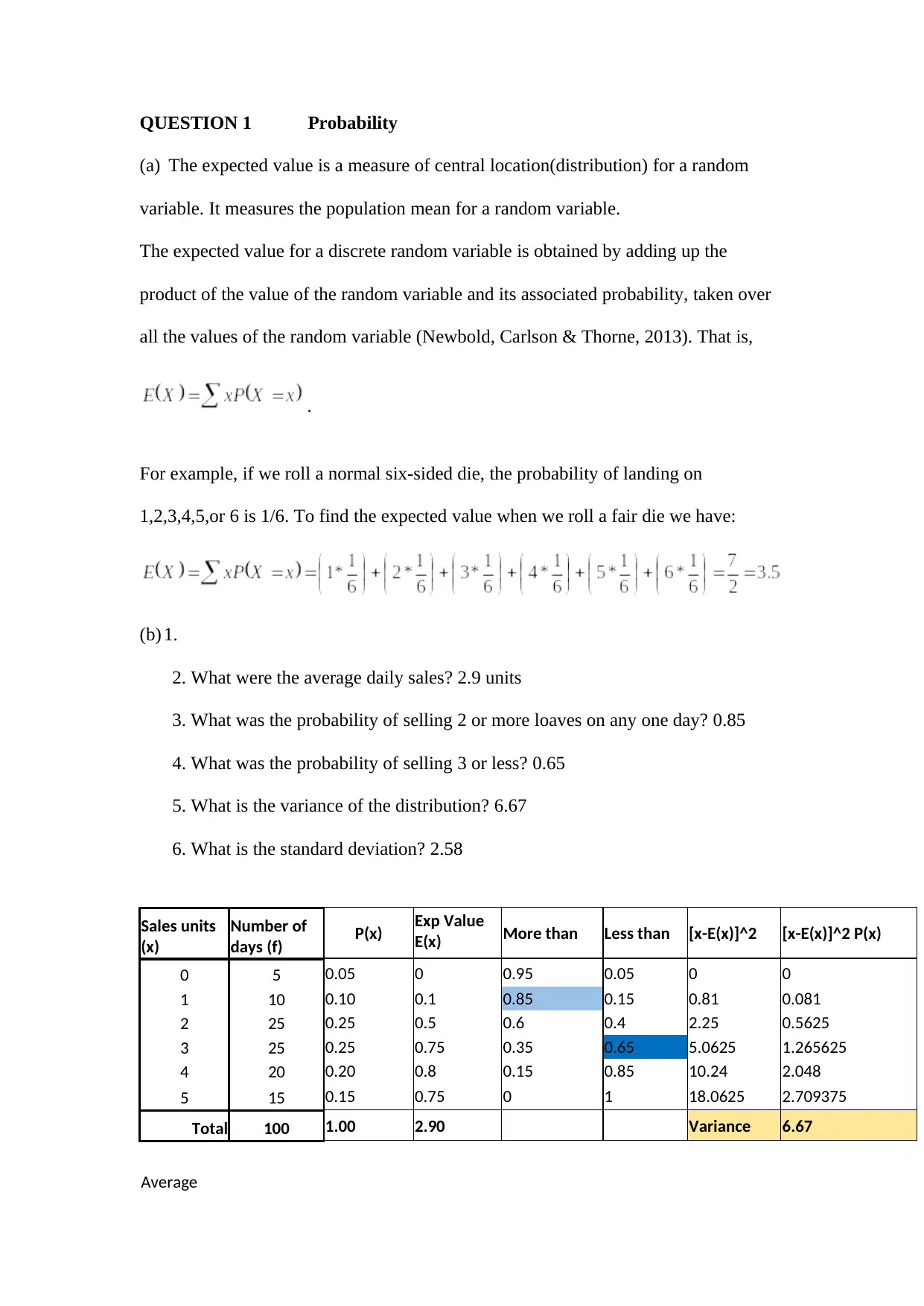
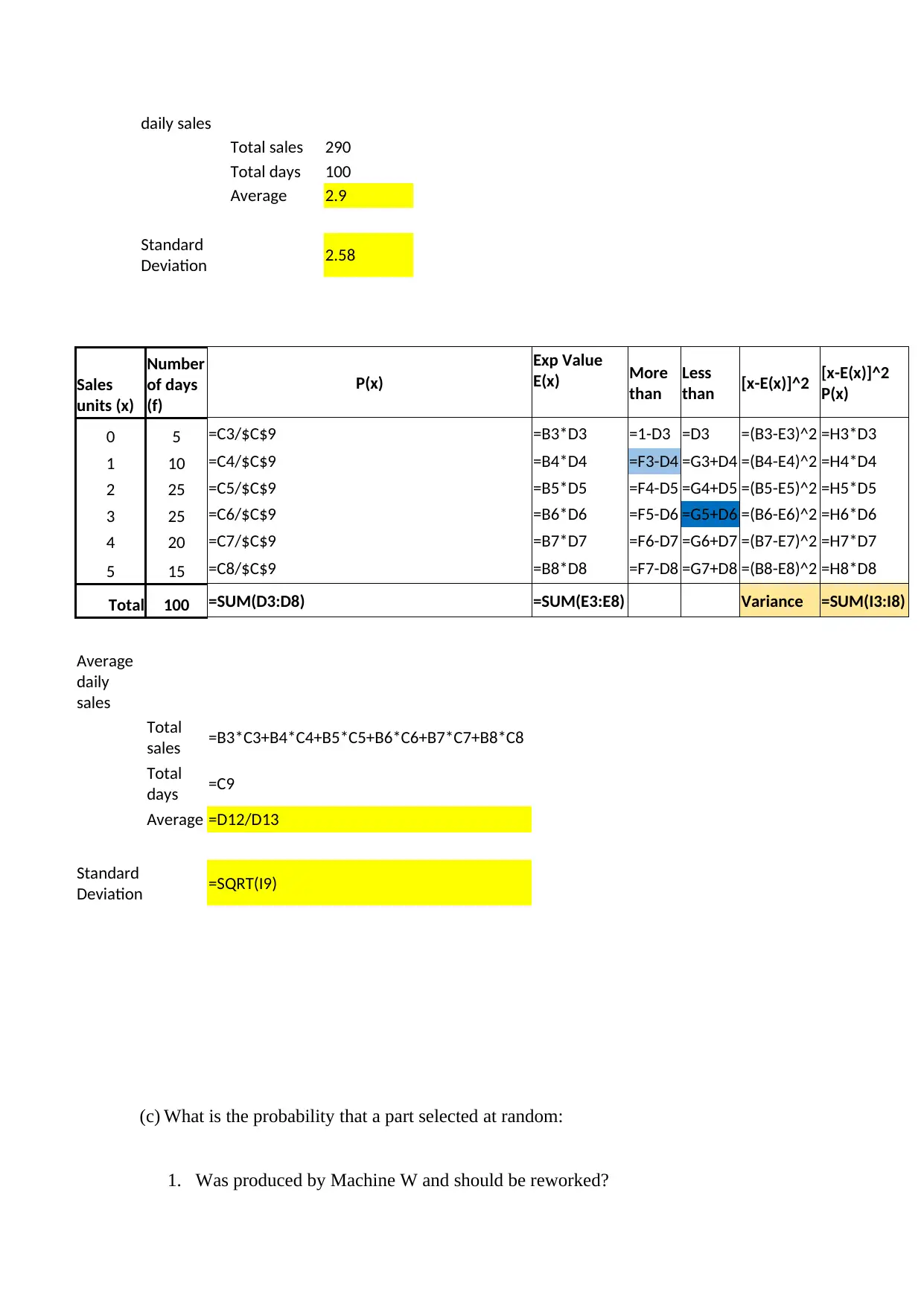
This assignment delves into probability and statistics, starting with the definition and calculation of expected value for discrete probability distributions, illustrated with the example of rolling a fair die. It proceeds to analyze daily sales data of sourdough bread, calculating average sales, probabilities of selling certain quantities, variance, and standard deviation using Excel. The assignment further explores conditional probabilities related to machine production and quality control, followed by calculations involving normal distributions to determine probabilities related to apple sales. It concludes with research questions on the average age and life expectancy in Australia, employment rates, and a hypothesis test for age discrimination using statistical decision-making principles and quality control measures. Desklib provides similar solved assignments and past papers for students.
1 out of 6











![[object Object]](/_next/static/media/star-bottom.7253800d.svg)