Calculating Minimum Damping Ratio for Overshoot
VerifiedAdded on 2023/01/23
|12
|2820
|60
AI Summary
In this question, we are asked to calculate the minimum damping ratio required for overshoot using a specific formula. The data required for the calculation is missing, so we suggest verifying the formula with the provided notes. We provide the correct formula and calculate the minimum damping ratio. The result is 0.3183.
Contribute Materials
Your contribution can guide someone’s learning journey. Share your
documents today.
Question 1.1:
In the question it is asked to calculate the minimum damping ratio required for Mp ≤ 10%
from the formula mentioned in your notes. Data missing for calculation of overshoot Mp ≤
10% as the notes formula in unavailable data is missing.
Though the following formula can be used for calculation of maximum overshoot, Mp. I
would suggest you to verify the below formula used for the calculation with the mentioned
notes formula.
Mp=e
−ζπ
√ ¿¿¿ ¿
Mp ≤ 10 %
0.10=e −ζπ
√¿ ¿¿ ¿
log 0.10=−¿ −ζπ
√ ¿ ¿ ¿ ¿
−1= −ζπ
√ ¿ ¿ ¿
1−ζ2−ζ 2 π2=0
ζ 2= 1
1+ π2
ζ =0.3183
The minimum damping ratio of the dominant poles for the overshoot, Mp is required to be
0.3183.
Question 1.2 Using the formula from your notes, calculate the minimum damped frequency, ωd = ωn
p1 − ζ2, of
the dominant poles for a peak time tp ≤ 0.5 sec.
The mentioned formula for calculating the minimum damping frequency in terms of natural
frequency is incorrect. Therefore I am writing the correct formula need to be used for tζhe
calculation. I would suggest you to verify with the formula provided in your notes. As you
can see there is no P present in the mention transfer function of the plant.
wd =wn √(1−ζ2 ¿)¿
ζ =0.3183
In the question it is asked to calculate the minimum damping ratio required for Mp ≤ 10%
from the formula mentioned in your notes. Data missing for calculation of overshoot Mp ≤
10% as the notes formula in unavailable data is missing.
Though the following formula can be used for calculation of maximum overshoot, Mp. I
would suggest you to verify the below formula used for the calculation with the mentioned
notes formula.
Mp=e
−ζπ
√ ¿¿¿ ¿
Mp ≤ 10 %
0.10=e −ζπ
√¿ ¿¿ ¿
log 0.10=−¿ −ζπ
√ ¿ ¿ ¿ ¿
−1= −ζπ
√ ¿ ¿ ¿
1−ζ2−ζ 2 π2=0
ζ 2= 1
1+ π2
ζ =0.3183
The minimum damping ratio of the dominant poles for the overshoot, Mp is required to be
0.3183.
Question 1.2 Using the formula from your notes, calculate the minimum damped frequency, ωd = ωn
p1 − ζ2, of
the dominant poles for a peak time tp ≤ 0.5 sec.
The mentioned formula for calculating the minimum damping frequency in terms of natural
frequency is incorrect. Therefore I am writing the correct formula need to be used for tζhe
calculation. I would suggest you to verify with the formula provided in your notes. As you
can see there is no P present in the mention transfer function of the plant.
wd =wn √(1−ζ2 ¿)¿
ζ =0.3183
Secure Best Marks with AI Grader
Need help grading? Try our AI Grader for instant feedback on your assignments.
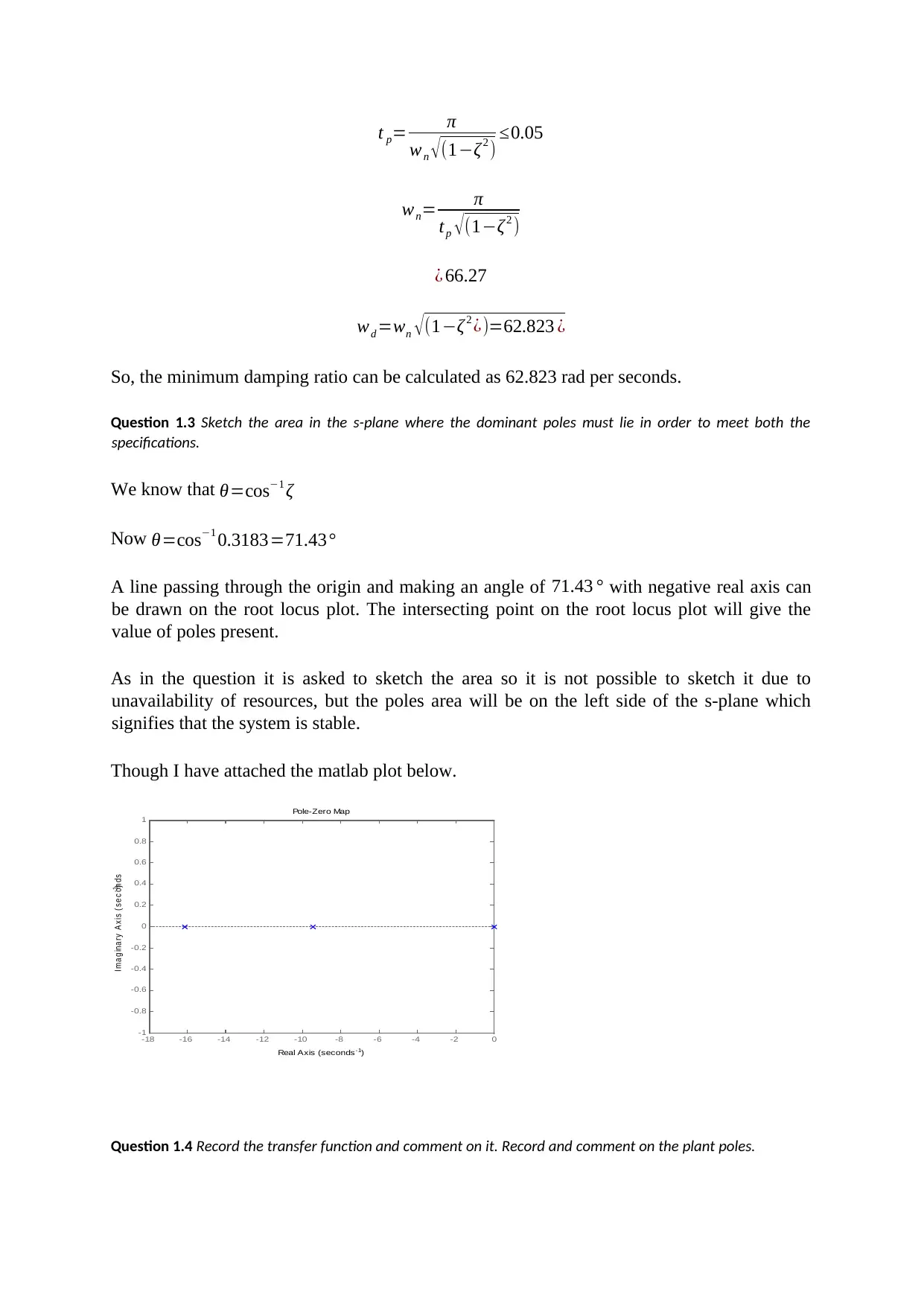
t p= π
wn √(1−ζ2 ) ≤0.05
wn= π
tp √(1−ζ2 )
¿ 66.27
wd =wn √ (1−ζ2 ¿)=62.823 ¿
So, the minimum damping ratio can be calculated as 62.823 rad per seconds.
Question 1.3 Sketch the area in the s-plane where the dominant poles must lie in order to meet both the
specifications.
We know that θ=cos−1 ζ
Now θ=cos−1 0.3183=71.43°
A line passing through the origin and making an angle of 71.43 ° with negative real axis can
be drawn on the root locus plot. The intersecting point on the root locus plot will give the
value of poles present.
As in the question it is asked to sketch the area so it is not possible to sketch it due to
unavailability of resources, but the poles area will be on the left side of the s-plane which
signifies that the system is stable.
Though I have attached the matlab plot below.
-18 -16 -14 -12 -10 -8 -6 -4 -2 0
-1
-0.8
-0.6
-0.4
-0.2
0
0.2
0.4
0.6
0.8
1
Pole-Zero Map
Real Axis (seconds -1
)
Im a g in a r y A x is ( s e c o n d s- 1
)
Question 1.4 Record the transfer function and comment on it. Record and comment on the plant poles.
wn √(1−ζ2 ) ≤0.05
wn= π
tp √(1−ζ2 )
¿ 66.27
wd =wn √ (1−ζ2 ¿)=62.823 ¿
So, the minimum damping ratio can be calculated as 62.823 rad per seconds.
Question 1.3 Sketch the area in the s-plane where the dominant poles must lie in order to meet both the
specifications.
We know that θ=cos−1 ζ
Now θ=cos−1 0.3183=71.43°
A line passing through the origin and making an angle of 71.43 ° with negative real axis can
be drawn on the root locus plot. The intersecting point on the root locus plot will give the
value of poles present.
As in the question it is asked to sketch the area so it is not possible to sketch it due to
unavailability of resources, but the poles area will be on the left side of the s-plane which
signifies that the system is stable.
Though I have attached the matlab plot below.
-18 -16 -14 -12 -10 -8 -6 -4 -2 0
-1
-0.8
-0.6
-0.4
-0.2
0
0.2
0.4
0.6
0.8
1
Pole-Zero Map
Real Axis (seconds -1
)
Im a g in a r y A x is ( s e c o n d s- 1
)
Question 1.4 Record the transfer function and comment on it. Record and comment on the plant poles.
0.956
Transfer Function, G= ----------------------------
0.006572 s^3 + 0.168 s^2 + s
The above transfer function replies that the system is a third order continuous time system
having three poles on its left plane. These poles are present on the negative side of the real
axis. The pole locations are at 0, -16.1290, and- 9.4340, which says that the system is a stable
system.
-18 -16 -14 -12 -10 -8 -6 -4 -2 0
-1
-0.8
-0.6
-0.4
-0.2
0
0.2
0.4
0.6
0.8
1
Pole-Zero Map
Real Axis (seconds-1)
Imaginary Axis (seconds-1)
Question 1.5 What will happen if you try to obtain the plant open loop step response? Explain why. Obtain the
open loop impulse response by impulse(G);
The open loop step response of the plant is shown in the figure below. The steady state error
possessed by a closed loop control system depends on the input and the open loop transfer
function. The actual output of a plant control system may be in any of the physical form of
position, velocity or acceleration. For evaluating steady state error the input function is
specified as unit step for displacement, unit ramp for velocity and unit parabolic for
acceleration. So applying unit step input will possess the result for the physical quantity
displacement or voltage.
0 5 10 15 20 25
0
5
10
15
20
25
Step Response
Time (seconds)
Amplitude
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
Impulse Response
Time (seconds)
Amplitude
Transfer Function, G= ----------------------------
0.006572 s^3 + 0.168 s^2 + s
The above transfer function replies that the system is a third order continuous time system
having three poles on its left plane. These poles are present on the negative side of the real
axis. The pole locations are at 0, -16.1290, and- 9.4340, which says that the system is a stable
system.
-18 -16 -14 -12 -10 -8 -6 -4 -2 0
-1
-0.8
-0.6
-0.4
-0.2
0
0.2
0.4
0.6
0.8
1
Pole-Zero Map
Real Axis (seconds-1)
Imaginary Axis (seconds-1)
Question 1.5 What will happen if you try to obtain the plant open loop step response? Explain why. Obtain the
open loop impulse response by impulse(G);
The open loop step response of the plant is shown in the figure below. The steady state error
possessed by a closed loop control system depends on the input and the open loop transfer
function. The actual output of a plant control system may be in any of the physical form of
position, velocity or acceleration. For evaluating steady state error the input function is
specified as unit step for displacement, unit ramp for velocity and unit parabolic for
acceleration. So applying unit step input will possess the result for the physical quantity
displacement or voltage.
0 5 10 15 20 25
0
5
10
15
20
25
Step Response
Time (seconds)
Amplitude
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
Impulse Response
Time (seconds)
Amplitude
Question 1.6 Explain this response characteristics.
The curve shows unit impulse response of a third order open loop transfer function. The
system represents an overdamped response with having a larger value of steady state point. It
has a Settling time of 0.506 sec with no overshoot and peak time.
Proportional controller design by Bode plot:
Question 2.1 Explain the Bode plot characteristics.
For Kp = 10, we obtain the following bode plot. This response shows the system is closed
loop stable system with GM as 8.15 dB at frequency 12.3 rad per sec. And PM is 28.3
degree.
10-1 100 101 102 103
-270
-225
-180
-135
-90
Phase (deg)
Bode Diagram
Frequency (rad/s)
-150
-100
-50
0
50
System: G
Gain Margin (dB): 8.15
At frequency (rad/s): 12.3
Closed loop stable? Yes
Magnitude (dB)
Question 2.2 Find the limiting value of kp for system stability. Show the workings on the Bode plot.
The limiting value of kp for this system stability is 0 < kp < 26.75
The curve shows unit impulse response of a third order open loop transfer function. The
system represents an overdamped response with having a larger value of steady state point. It
has a Settling time of 0.506 sec with no overshoot and peak time.
Proportional controller design by Bode plot:
Question 2.1 Explain the Bode plot characteristics.
For Kp = 10, we obtain the following bode plot. This response shows the system is closed
loop stable system with GM as 8.15 dB at frequency 12.3 rad per sec. And PM is 28.3
degree.
10-1 100 101 102 103
-270
-225
-180
-135
-90
Phase (deg)
Bode Diagram
Frequency (rad/s)
-150
-100
-50
0
50
System: G
Gain Margin (dB): 8.15
At frequency (rad/s): 12.3
Closed loop stable? Yes
Magnitude (dB)
Question 2.2 Find the limiting value of kp for system stability. Show the workings on the Bode plot.
The limiting value of kp for this system stability is 0 < kp < 26.75
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
Bode plot taking kp= 29, beyond the limiting value. The system is unstable.
10
-1 10
0 10
1 10
2 10
3
-270
-225
-180
-135
-90
P h a s e ( d e g )
Bode Diagram
Frequency (rad/s)
-150
-100
-50
0
50
100 System: G
Gain Margin (dB): -1.1
At frequency (rad/s): 12.3
Closed loop stable? No
M a g n it u d e ( d B )
Question 2.3 From the Bode plot, determine the value of kp required for Mp = 10% assuming
PM ≈ 100ζ for PM < 70deg
where PM is the phase margin. Show the workings on the Bode plot.
The ζ value for a 10% overshoot can be calculated as 0.3183. Therefore, the value of kp
should be 2.2 to get an overshoot of 10%. The bode plot for overshoot 10% is shown below.
Bode Diagram
Frequency (rad/s)
10-1 100 101 102 103
-270
-225
-180
-135
-90
System: G
Phase Margin (deg): 69.8
Delay Margin (sec): 0.572
At frequency (rad/s): 2.13
Closed loop stable? Yes
Phase (deg)
-150
-100
-50
0
50 System: G
Gain Margin (dB): 21.3
At frequency (rad/s): 12.3
Closed loop stable? Yes
Magnitude (dB)
10
-1 10
0 10
1 10
2 10
3
-270
-225
-180
-135
-90
P h a s e ( d e g )
Bode Diagram
Frequency (rad/s)
-150
-100
-50
0
50
100 System: G
Gain Margin (dB): -1.1
At frequency (rad/s): 12.3
Closed loop stable? No
M a g n it u d e ( d B )
Question 2.3 From the Bode plot, determine the value of kp required for Mp = 10% assuming
PM ≈ 100ζ for PM < 70deg
where PM is the phase margin. Show the workings on the Bode plot.
The ζ value for a 10% overshoot can be calculated as 0.3183. Therefore, the value of kp
should be 2.2 to get an overshoot of 10%. The bode plot for overshoot 10% is shown below.
Bode Diagram
Frequency (rad/s)
10-1 100 101 102 103
-270
-225
-180
-135
-90
System: G
Phase Margin (deg): 69.8
Delay Margin (sec): 0.572
At frequency (rad/s): 2.13
Closed loop stable? Yes
Phase (deg)
-150
-100
-50
0
50 System: G
Gain Margin (dB): 21.3
At frequency (rad/s): 12.3
Closed loop stable? Yes
Magnitude (dB)
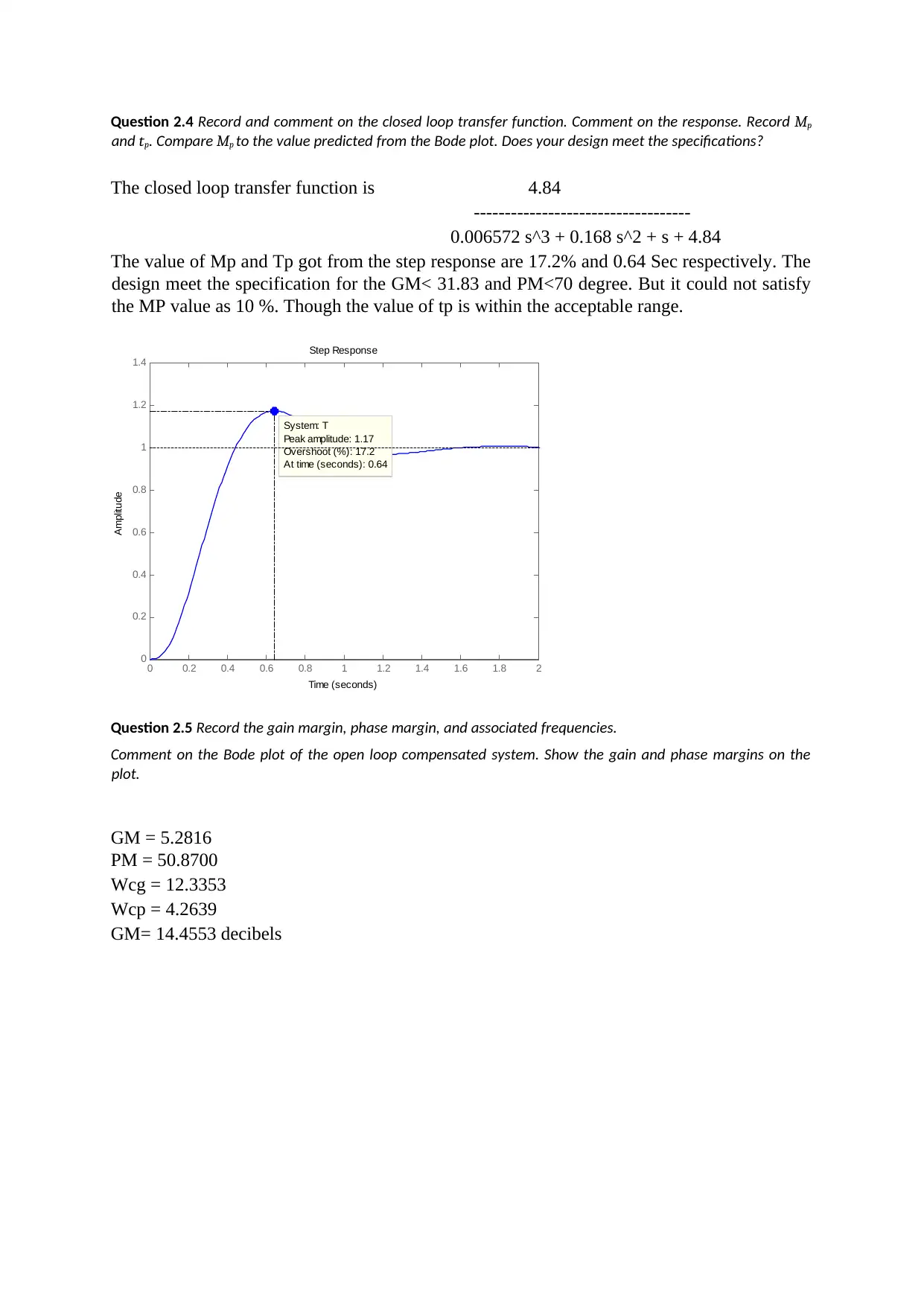
Question 2.4 Record and comment on the closed loop transfer function. Comment on the response. Record Mp
and tp. Compare Mp to the value predicted from the Bode plot. Does your design meet the specifications?
The closed loop transfer function is 4.84
-----------------------------------
0.006572 s^3 + 0.168 s^2 + s + 4.84
The value of Mp and Tp got from the step response are 17.2% and 0.64 Sec respectively. The
design meet the specification for the GM< 31.83 and PM<70 degree. But it could not satisfy
the MP value as 10 %. Though the value of tp is within the acceptable range.
Step Response
Time (seconds)
Amplitude
0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2
0
0.2
0.4
0.6
0.8
1
1.2
1.4
System: T
Peak amplitude: 1.17
Overshoot (%): 17.2
At time (seconds): 0.64
Question 2.5 Record the gain margin, phase margin, and associated frequencies.
Comment on the Bode plot of the open loop compensated system. Show the gain and phase margins on the
plot.
GM = 5.2816
PM = 50.8700
Wcg = 12.3353
Wcp = 4.2639
GM= 14.4553 decibels
and tp. Compare Mp to the value predicted from the Bode plot. Does your design meet the specifications?
The closed loop transfer function is 4.84
-----------------------------------
0.006572 s^3 + 0.168 s^2 + s + 4.84
The value of Mp and Tp got from the step response are 17.2% and 0.64 Sec respectively. The
design meet the specification for the GM< 31.83 and PM<70 degree. But it could not satisfy
the MP value as 10 %. Though the value of tp is within the acceptable range.
Step Response
Time (seconds)
Amplitude
0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2
0
0.2
0.4
0.6
0.8
1
1.2
1.4
System: T
Peak amplitude: 1.17
Overshoot (%): 17.2
At time (seconds): 0.64
Question 2.5 Record the gain margin, phase margin, and associated frequencies.
Comment on the Bode plot of the open loop compensated system. Show the gain and phase margins on the
plot.
GM = 5.2816
PM = 50.8700
Wcg = 12.3353
Wcp = 4.2639
GM= 14.4553 decibels
Bode Diagram
Frequency (rad/s)
-150
-100
-50
0
50 System: untitled1
Gain Margin (dB): 14.5
At frequency (rad/s): 12.3
Closed loop stable? Yes
M a g n itu d e ( d B )
10
-1 10
0 10
1 10
2 10
3
-270
-225
-180
-135
-90
System: untitled1
Phase Margin (deg): 50.9
Delay Margin (sec): 0.208
At frequency (rad/s): 4.26
Closed loop stable? Yes
P h a s e ( d e g )
Question 3.1 What will be the system type if a PID controller is used on this plant? For zero steady state error
(to unity step references) for this plant, is an integrator required in the controller?
If a PID controller is used in this plant it will be an Industrial automation system. Yes to get a
zero steady state error integrator is required. Because by using only proportional controller
the system cannot reach the steady state value. It remains some amount of offset.
Question 3.2 What are the advantages and disadvantages of not using integral action (i.e., using P+D control)?
Disadvantage:
Steady state error cannot be reduced to zero.
Some offset always remain.
Cannot apply for fast moving process control like flow, pressure.
Advantage:
System stability increases.
Maximum overshoot, Mp decreases.
Settling time, ts decreases.
Question 3.3 From the plot, measure Mp and tp. Does your design meet the specifications? Record the final
values of kp and kd. Record the transfer function K(s), the system open loop transfer function L(s) and the
closed loop transfer function T(s).
From the plot we got the value of Mp as 10.3% and tp as 0.155 sec.
Yes, this design meets the specification.
The final value of kp =2.2 and kd = 3.8.
3. 4 84s + 2.2
Frequency (rad/s)
-150
-100
-50
0
50 System: untitled1
Gain Margin (dB): 14.5
At frequency (rad/s): 12.3
Closed loop stable? Yes
M a g n itu d e ( d B )
10
-1 10
0 10
1 10
2 10
3
-270
-225
-180
-135
-90
System: untitled1
Phase Margin (deg): 50.9
Delay Margin (sec): 0.208
At frequency (rad/s): 4.26
Closed loop stable? Yes
P h a s e ( d e g )
Question 3.1 What will be the system type if a PID controller is used on this plant? For zero steady state error
(to unity step references) for this plant, is an integrator required in the controller?
If a PID controller is used in this plant it will be an Industrial automation system. Yes to get a
zero steady state error integrator is required. Because by using only proportional controller
the system cannot reach the steady state value. It remains some amount of offset.
Question 3.2 What are the advantages and disadvantages of not using integral action (i.e., using P+D control)?
Disadvantage:
Steady state error cannot be reduced to zero.
Some offset always remain.
Cannot apply for fast moving process control like flow, pressure.
Advantage:
System stability increases.
Maximum overshoot, Mp decreases.
Settling time, ts decreases.
Question 3.3 From the plot, measure Mp and tp. Does your design meet the specifications? Record the final
values of kp and kd. Record the transfer function K(s), the system open loop transfer function L(s) and the
closed loop transfer function T(s).
From the plot we got the value of Mp as 10.3% and tp as 0.155 sec.
Yes, this design meets the specification.
The final value of kp =2.2 and kd = 3.8.
3. 4 84s + 2.2
Secure Best Marks with AI Grader
Need help grading? Try our AI Grader for instant feedback on your assignments.
transfer function K(s) = -------------
0.02 s + 1
3.675 s + 2.103
L(S) = --------------------------------------------
0.0001314 s^4 + 0.009932 s^3 + 0.188 s^2 + s
3.675 s + 2.103
T(S) = ----------------------------------------------------------
0.0001314 s^4 + 0.009932 s^3 + 0.188 s^2 + 4.675 s + 2.103
Step Response
Time (seconds)
Amplitude
0 1 2 3 4 5 6 7 8
0
0.2
0.4
0.6
0.8
1
1.2
1.4 System: T
Peak amplitude: 1.1
Overshoot (%): 10.3
At time (seconds): 0.155
Question 3.4 the Bode plot of controller transfer function characteristics.
0.02 s + 1
3.675 s + 2.103
L(S) = --------------------------------------------
0.0001314 s^4 + 0.009932 s^3 + 0.188 s^2 + s
3.675 s + 2.103
T(S) = ----------------------------------------------------------
0.0001314 s^4 + 0.009932 s^3 + 0.188 s^2 + 4.675 s + 2.103
Step Response
Time (seconds)
Amplitude
0 1 2 3 4 5 6 7 8
0
0.2
0.4
0.6
0.8
1
1.2
1.4 System: T
Peak amplitude: 1.1
Overshoot (%): 10.3
At time (seconds): 0.155
Question 3.4 the Bode plot of controller transfer function characteristics.
10-2 10-1 100 101 102 103
0
30
60
90
Phase (deg)
Bode Diagram
Frequency (rad/s)
0
10
20
30
40
50
Magnitude (dB)
Question 3.5 Record the gain margin, phase margin, and associated frequencies. Show the gain margin and
phase margin on the Bode plot.
Bode Diagram
Frequency (rad/s)
-150
-100
-50
0
50 System: L
Gain Margin (dB): 10.8
At frequency (rad/s): 37.3
Closed loop stable? Yes
Magnitude (dB)
10-2 10-1 100 101 102 103 104
-270
-180
-90
0
System: L
Phase Margin (deg): 44.7
Delay Margin (sec): 0.0414
At frequency (rad/s): 18.9
Closed loop stable? Yes
Phase (deg)
0
30
60
90
Phase (deg)
Bode Diagram
Frequency (rad/s)
0
10
20
30
40
50
Magnitude (dB)
Question 3.5 Record the gain margin, phase margin, and associated frequencies. Show the gain margin and
phase margin on the Bode plot.
Bode Diagram
Frequency (rad/s)
-150
-100
-50
0
50 System: L
Gain Margin (dB): 10.8
At frequency (rad/s): 37.3
Closed loop stable? Yes
Magnitude (dB)
10-2 10-1 100 101 102 103 104
-270
-180
-90
0
System: L
Phase Margin (deg): 44.7
Delay Margin (sec): 0.0414
At frequency (rad/s): 18.9
Closed loop stable? Yes
Phase (deg)
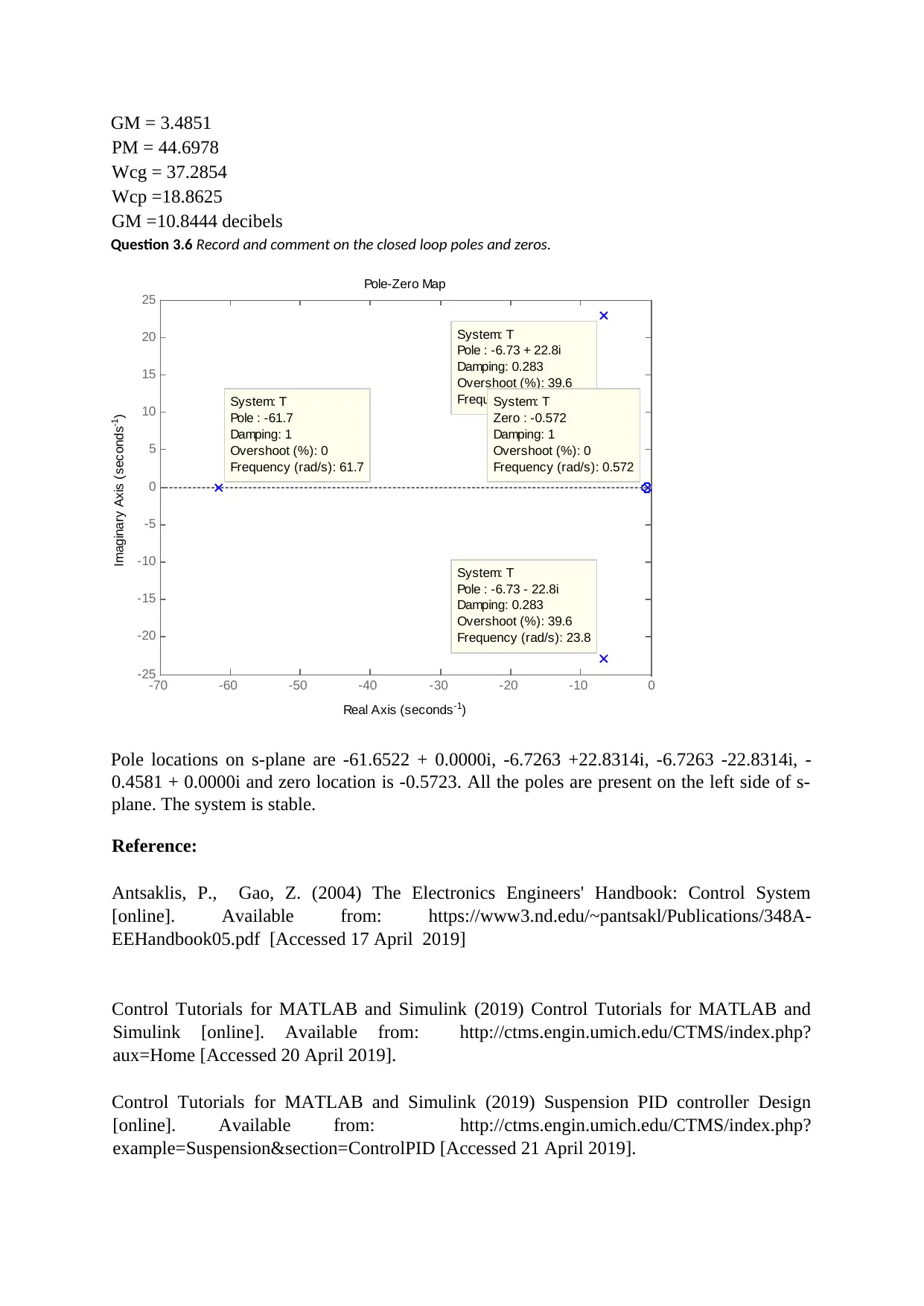
GM = 3.4851
PM = 44.6978
Wcg = 37.2854
Wcp =18.8625
GM =10.8444 decibels
Question 3.6 Record and comment on the closed loop poles and zeros.
Pole-Zero Map
Real Axis (seconds-1)
Imaginary Axis (seconds-1)
-70 -60 -50 -40 -30 -20 -10 0
-25
-20
-15
-10
-5
0
5
10
15
20
25
System: T
Pole : -6.73 + 22.8i
Damping: 0.283
Overshoot (%): 39.6
Frequency (rad/s): 23.8
System: T
Pole : -6.73 - 22.8i
Damping: 0.283
Overshoot (%): 39.6
Frequency (rad/s): 23.8
System: T
Zero : -0.572
Damping: 1
Overshoot (%): 0
Frequency (rad/s): 0.572
System: T
Pole : -61.7
Damping: 1
Overshoot (%): 0
Frequency (rad/s): 61.7
Pole locations on s-plane are -61.6522 + 0.0000i, -6.7263 +22.8314i, -6.7263 -22.8314i, -
0.4581 + 0.0000i and zero location is -0.5723. All the poles are present on the left side of s-
plane. The system is stable.
Reference:
Antsaklis, P., Gao, Z. (2004) The Electronics Engineers' Handbook: Control System
[online]. Available from: https://www3.nd.edu/~pantsakl/Publications/348A-
EEHandbook05.pdf [Accessed 17 April 2019]
Control Tutorials for MATLAB and Simulink (2019) Control Tutorials for MATLAB and
Simulink [online]. Available from: http://ctms.engin.umich.edu/CTMS/index.php?
aux=Home [Accessed 20 April 2019].
Control Tutorials for MATLAB and Simulink (2019) Suspension PID controller Design
[online]. Available from: http://ctms.engin.umich.edu/CTMS/index.php?
example=Suspension§ion=ControlPID [Accessed 21 April 2019].
PM = 44.6978
Wcg = 37.2854
Wcp =18.8625
GM =10.8444 decibels
Question 3.6 Record and comment on the closed loop poles and zeros.
Pole-Zero Map
Real Axis (seconds-1)
Imaginary Axis (seconds-1)
-70 -60 -50 -40 -30 -20 -10 0
-25
-20
-15
-10
-5
0
5
10
15
20
25
System: T
Pole : -6.73 + 22.8i
Damping: 0.283
Overshoot (%): 39.6
Frequency (rad/s): 23.8
System: T
Pole : -6.73 - 22.8i
Damping: 0.283
Overshoot (%): 39.6
Frequency (rad/s): 23.8
System: T
Zero : -0.572
Damping: 1
Overshoot (%): 0
Frequency (rad/s): 0.572
System: T
Pole : -61.7
Damping: 1
Overshoot (%): 0
Frequency (rad/s): 61.7
Pole locations on s-plane are -61.6522 + 0.0000i, -6.7263 +22.8314i, -6.7263 -22.8314i, -
0.4581 + 0.0000i and zero location is -0.5723. All the poles are present on the left side of s-
plane. The system is stable.
Reference:
Antsaklis, P., Gao, Z. (2004) The Electronics Engineers' Handbook: Control System
[online]. Available from: https://www3.nd.edu/~pantsakl/Publications/348A-
EEHandbook05.pdf [Accessed 17 April 2019]
Control Tutorials for MATLAB and Simulink (2019) Control Tutorials for MATLAB and
Simulink [online]. Available from: http://ctms.engin.umich.edu/CTMS/index.php?
aux=Home [Accessed 20 April 2019].
Control Tutorials for MATLAB and Simulink (2019) Suspension PID controller Design
[online]. Available from: http://ctms.engin.umich.edu/CTMS/index.php?
example=Suspension§ion=ControlPID [Accessed 21 April 2019].
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
Electrical 4 U (2019) Control System | Closed Loop Open Loop Control System. [online].
Available from: https://www.electrical4u.com/control-system-closed-loop-open-loop-control-
system/ [Accessed 21 April 2019].
Encyclopedia Britanica (2019) Control Systems Technology. [online]. Available from:
https://www.britannica.com/technology/control-system [Accessed 21 April 2019].
Java T point (2019) Control Systems Tutorial. [online]. Available from:
https://www.javatpoint.com/control-system-tutorial [Accessed 21 April 2019].
Manke, B, S. (2007) Linear control systems: with MATLAB applications. 11th ed.
Delhi: Khanna Publishers.
MathWorks (2019) Automatically Tunned PID controller Gain [online]. Available from:
https://in.mathworks.com/discovery/pid-tuning.html [Accessed 19 April 2019].
MathWorks (2019) Control Systems Toolbox: Code Examples. [online]. Available from:
https://in.mathworks.com/products/control/code-examples.html [Accessed 20 April 2019].
MathWorks (2019) Control Systems Toolbox: Design and Analyse Control System [online].
Available from: https://in.mathworks.com/products/control.html [Accessed 19 April 2019].
MathWorks (2019) Control Systems Toolbox: Dynamic System Models. [online]. Available
from: https://in.mathworks.com/help/control/examples.html [Accessed 21 April 2019].
MathWorks (2019) PID controller design at the command line [online]. Available from:
https://in.mathworks.com/help/control/ug/pid-controller-design-at-the-command-line.html
[Accessed 18 April 2019].
MathWorks (2019) PID control with MATLAB and Simulink [online]. Available from:
https://in.mathworks.com/discovery/pid-control.html [Accessed 21 April 2019].
MathWorks (2019) Videos and Webinar : PID control made easy [online]. Available from:
https://in.mathworks.com/videos/pid-control-made-easy-81646.html [Accessed 20 April
2019].
Physics Forum (2012) Damping ratio and Maximum overshoot relation. [online]. Available
from:
https://www.physicsforums.com/threads/damping-ratio-and-maximum-overshoot-
relation.646083_May11 [Accessed 21 April 2019].
Techopedia (2019) Control Systems Technology. [online]. Available from:
https://www.techopedia.com/definition/33169/control-system [Accessed 17 April 2019].
Available from: https://www.electrical4u.com/control-system-closed-loop-open-loop-control-
system/ [Accessed 21 April 2019].
Encyclopedia Britanica (2019) Control Systems Technology. [online]. Available from:
https://www.britannica.com/technology/control-system [Accessed 21 April 2019].
Java T point (2019) Control Systems Tutorial. [online]. Available from:
https://www.javatpoint.com/control-system-tutorial [Accessed 21 April 2019].
Manke, B, S. (2007) Linear control systems: with MATLAB applications. 11th ed.
Delhi: Khanna Publishers.
MathWorks (2019) Automatically Tunned PID controller Gain [online]. Available from:
https://in.mathworks.com/discovery/pid-tuning.html [Accessed 19 April 2019].
MathWorks (2019) Control Systems Toolbox: Code Examples. [online]. Available from:
https://in.mathworks.com/products/control/code-examples.html [Accessed 20 April 2019].
MathWorks (2019) Control Systems Toolbox: Design and Analyse Control System [online].
Available from: https://in.mathworks.com/products/control.html [Accessed 19 April 2019].
MathWorks (2019) Control Systems Toolbox: Dynamic System Models. [online]. Available
from: https://in.mathworks.com/help/control/examples.html [Accessed 21 April 2019].
MathWorks (2019) PID controller design at the command line [online]. Available from:
https://in.mathworks.com/help/control/ug/pid-controller-design-at-the-command-line.html
[Accessed 18 April 2019].
MathWorks (2019) PID control with MATLAB and Simulink [online]. Available from:
https://in.mathworks.com/discovery/pid-control.html [Accessed 21 April 2019].
MathWorks (2019) Videos and Webinar : PID control made easy [online]. Available from:
https://in.mathworks.com/videos/pid-control-made-easy-81646.html [Accessed 20 April
2019].
Physics Forum (2012) Damping ratio and Maximum overshoot relation. [online]. Available
from:
https://www.physicsforums.com/threads/damping-ratio-and-maximum-overshoot-
relation.646083_May11 [Accessed 21 April 2019].
Techopedia (2019) Control Systems Technology. [online]. Available from:
https://www.techopedia.com/definition/33169/control-system [Accessed 17 April 2019].
Twalsh123 (2014) MatLAB PID Examples. Available
from: https://www.youtube.com/watch?v=lfMMPe7s9nU [Accessed 17 April 2019]
from: https://www.youtube.com/watch?v=lfMMPe7s9nU [Accessed 17 April 2019]
1 out of 12
![[object Object]](/_next/image/?url=%2F_next%2Fstatic%2Fmedia%2Flogo.6d15ce61.png&w=640&q=75){kind=small}
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
© 2024 | Zucol Services PVT LTD | All rights reserved.