Probability & Stats: Hypothesis Testing and Distributions
VerifiedAdded on 2023/04/25
|8
|1004
|492
Homework Assignment
AI Summary
This assignment provides detailed solutions to a range of probability and statistics problems. It includes calculations for confidence intervals, hypothesis testing, and normal distribution applications. Specifically, it addresses questions related to mobile phone user charges, biased coin tosses, binom...

Question 4
n = 277
x = 69
^p= x
n = 69
277 =0.2491
79.6% confidence interval for portion of adult female shopper who request a rain check in such
situation
= ^p ¿ ¿α/2 * √ ^p(1− ^p)
n )
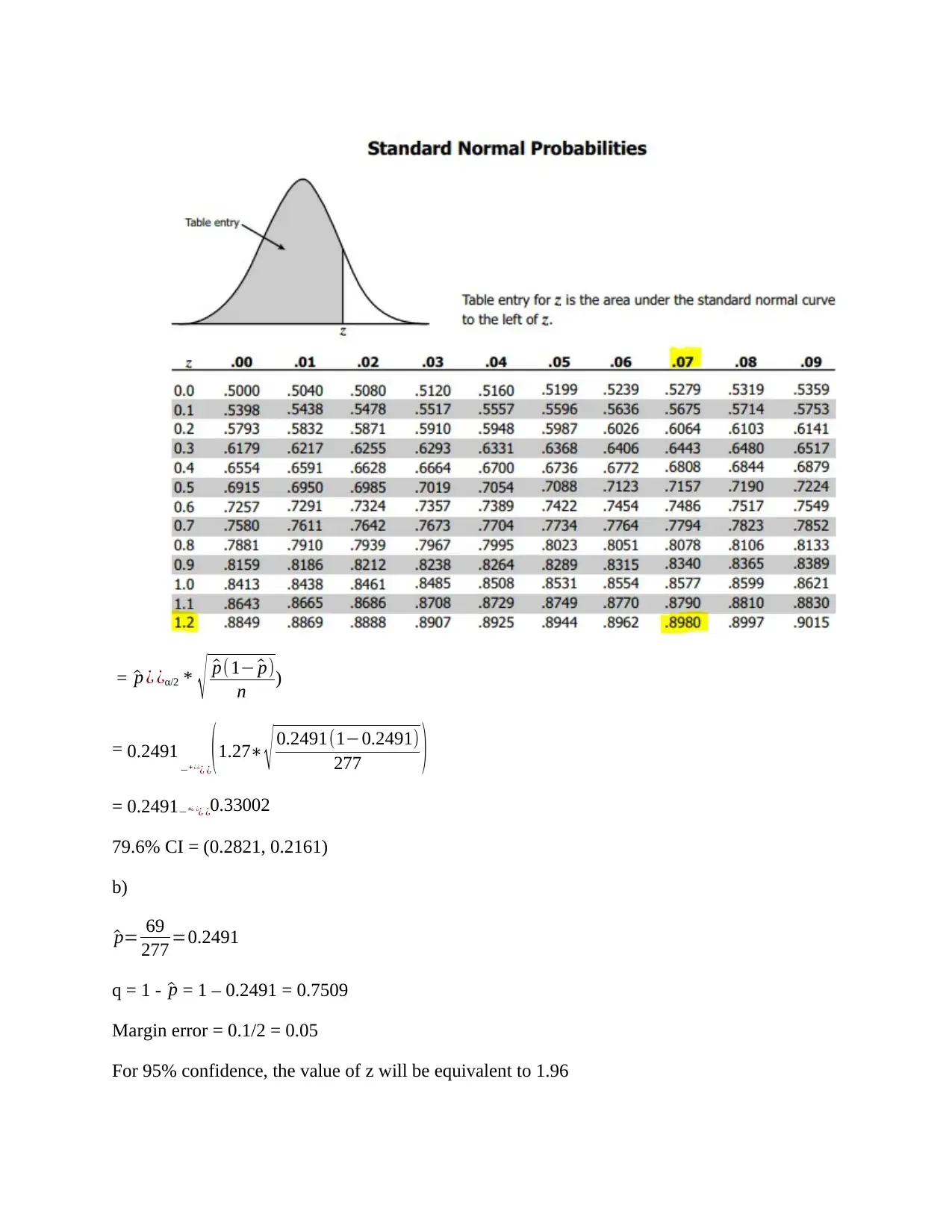
Zα/2 value of 79.6% confidence level is determined as follows;
The confidence level would be subtracted from 1 and the result divided by two in order to find
the value of alpha level which will be representing the one tail area.
(1 – 0.796)/2 = 0.102
Subtract the result from one, the area is then looked at the middle of the z – table in order to
determine the value of the z score.
1 – 0.102 = 0.898
Checking it at z – table as shown
Z – score = 1.27) as highlighted on the z- table diagram below)
n = 277
x = 69
^p= x
n = 69
277 =0.2491
79.6% confidence interval for portion of adult female shopper who request a rain check in such
situation
= ^p ¿ ¿α/2 * √ ^p(1− ^p)
n )
Zα/2 value of 79.6% confidence level is determined as follows;
The confidence level would be subtracted from 1 and the result divided by two in order to find
the value of alpha level which will be representing the one tail area.
(1 – 0.796)/2 = 0.102
Subtract the result from one, the area is then looked at the middle of the z – table in order to
determine the value of the z score.
1 – 0.102 = 0.898
Checking it at z – table as shown
Z – score = 1.27) as highlighted on the z- table diagram below)
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
= ^p ¿ ¿α/2 * √ ^p(1− ^p)
n )
= 0.2491 ( 1.27∗ √ 0.2491(1−0.2491)
277 )− ¿+ ¿¿ ¿
= 0.2491 0.33002− ¿+¿ ¿ ¿
79.6% CI = (0.2821, 0.2161)
b)
^p= 69
277 =0.2491
q = 1 - ^p = 1 – 0.2491 = 0.7509
Margin error = 0.1/2 = 0.05
For 95% confidence, the value of z will be equivalent to 1.96
n )
= 0.2491 ( 1.27∗ √ 0.2491(1−0.2491)
277 )− ¿+ ¿¿ ¿
= 0.2491 0.33002− ¿+¿ ¿ ¿
79.6% CI = (0.2821, 0.2161)
b)
^p= 69
277 =0.2491
q = 1 - ^p = 1 – 0.2491 = 0.7509
Margin error = 0.1/2 = 0.05
For 95% confidence, the value of z will be equivalent to 1.96

Size of sample required will be equivalent to
n = pq* ( z− score
E )
2
= 0.2491 * 0.7509* ( 1.96
0.05 )2
n = 287.427
n ≈ 287 (rounded off to next whole number)
Question 7
P(number 2 or less) = 2 / 6 = 1 / 3
Mean = np = 500 * 1/3 = 166.6667
Standard deviation = √(np(1− p))
= √ ( 500∗1
3 ∗2/3)
= 10.5409
Using normal approximation.,
P( X ≤ x) = P( Z < x+0.5 - mean / SD)
So,
P(X ≤ 150) = P( Z ≤ ¿150.5 - 166.6667 / 10.5409))
= P (Z ≤ -1.5337)
From the z-table shown on the diagram below, the probability will be equivalent to;
n = pq* ( z− score
E )
2
= 0.2491 * 0.7509* ( 1.96
0.05 )2
n = 287.427
n ≈ 287 (rounded off to next whole number)
Question 7
P(number 2 or less) = 2 / 6 = 1 / 3
Mean = np = 500 * 1/3 = 166.6667
Standard deviation = √(np(1− p))
= √ ( 500∗1
3 ∗2/3)
= 10.5409
Using normal approximation.,
P( X ≤ x) = P( Z < x+0.5 - mean / SD)
So,
P(X ≤ 150) = P( Z ≤ ¿150.5 - 166.6667 / 10.5409))
= P (Z ≤ -1.5337)
From the z-table shown on the diagram below, the probability will be equivalent to;
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
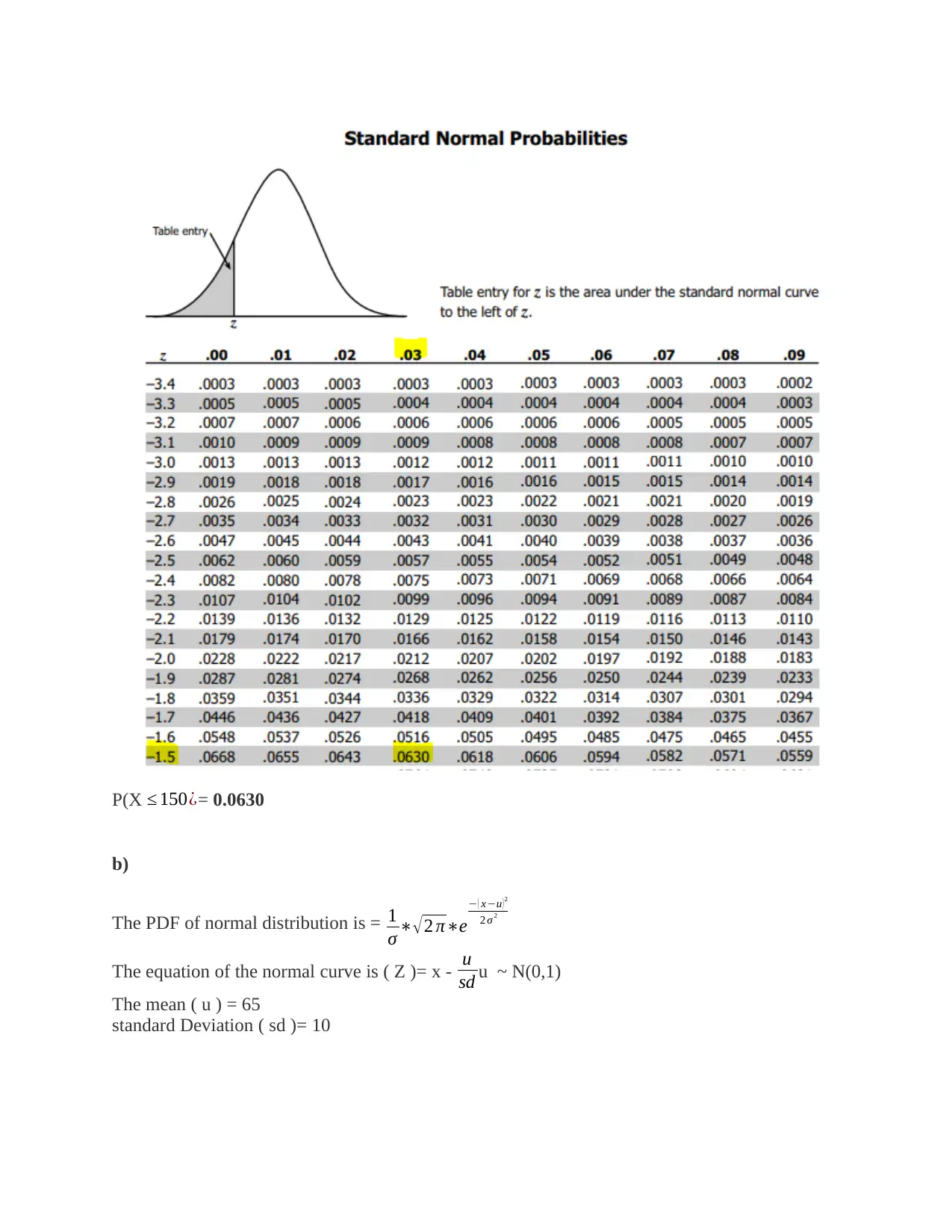
P(X ≤ 150¿= 0.0630
b)
The PDF of normal distribution is = 1
σ ∗√2 π∗e
− ( x−u )2
2 σ 2
The equation of the normal curve is ( Z )= x - u
sd u ~ N(0,1)
The mean ( u ) = 65
standard Deviation ( sd )= 10
b)
The PDF of normal distribution is = 1
σ ∗√2 π∗e
− ( x−u )2
2 σ 2
The equation of the normal curve is ( Z )= x - u
sd u ~ N(0,1)
The mean ( u ) = 65
standard Deviation ( sd )= 10
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
i)
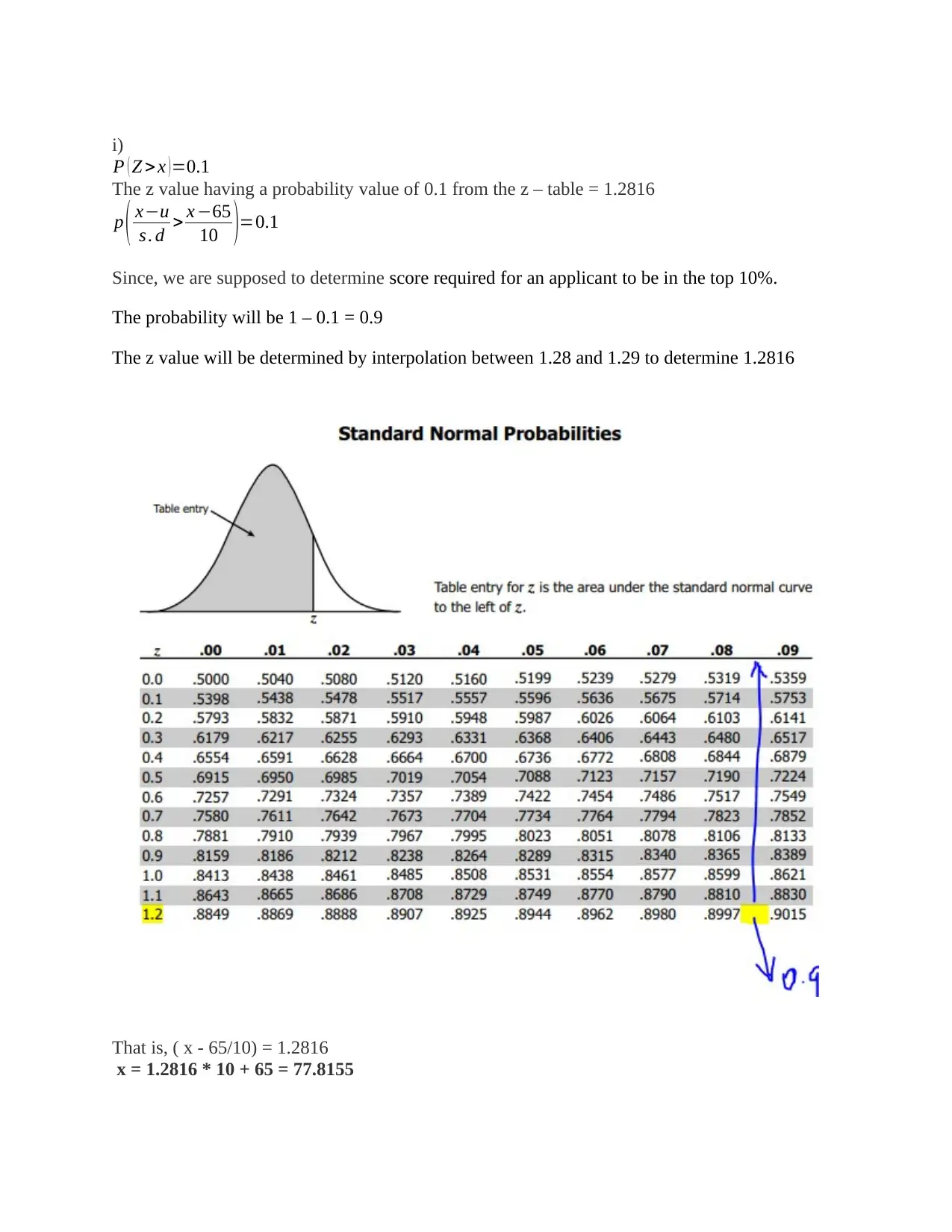
P ( Z > x )=0.1
The z value having a probability value of 0.1 from the z – table = 1.2816
p ( x−u
s . d > x −65
10 )=0.1
Since, we are supposed to determine score required for an applicant to be in the top 10%.
The probability will be 1 – 0.1 = 0.9
The z value will be determined by interpolation between 1.28 and 1.29 to determine 1.2816
That is, ( x - 65/10) = 1.2816
x = 1.2816 * 10 + 65 = 77.8155
P ( Z > x )=0.1
The z value having a probability value of 0.1 from the z – table = 1.2816
p ( x−u
s . d > x −65
10 )=0.1
Since, we are supposed to determine score required for an applicant to be in the top 10%.
The probability will be 1 – 0.1 = 0.9
The z value will be determined by interpolation between 1.28 and 1.29 to determine 1.2816
That is, ( x - 65/10) = 1.2816
x = 1.2816 * 10 + 65 = 77.8155
ii)
The PDF of normal distribution is = 1
σ ∗√2 π∗e
− ( x−u )2
2 σ 2
The equation of the normal curve is ( Z )= x - u
sd u ~ N(0,1)
mean of the sampling distribution ( x ) = 65
standard Deviation ( sd )= 10/ Sqrt ( 16 ) =2.5
sample size (n) = 16
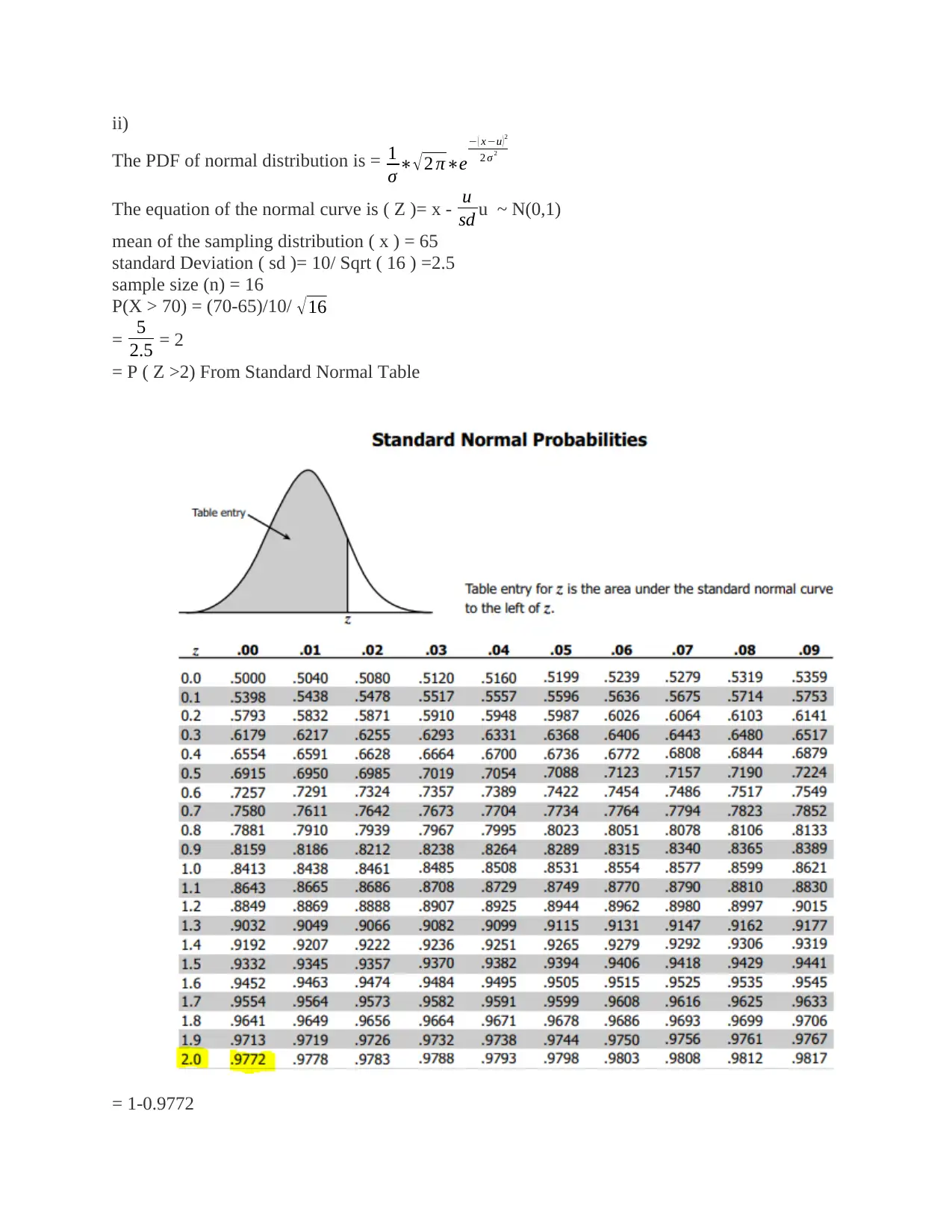
P(X > 70) = (70-65)/10/ √ 16
= 5
2.5 = 2
= P ( Z >2) From Standard Normal Table
= 1-0.9772
The PDF of normal distribution is = 1
σ ∗√2 π∗e
− ( x−u )2
2 σ 2
The equation of the normal curve is ( Z )= x - u
sd u ~ N(0,1)
mean of the sampling distribution ( x ) = 65
standard Deviation ( sd )= 10/ Sqrt ( 16 ) =2.5
sample size (n) = 16
P(X > 70) = (70-65)/10/ √ 16
= 5
2.5 = 2
= P ( Z >2) From Standard Normal Table
= 1-0.9772
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

= 0.0228
Question 8
n = 7, x= ∑ x
n = 49.3
7 =7.0429
s.d = √ 1
n−1 ¿ ¿
= √ 1
6 ¿ ¿ = 0.5028
a) 98% confidence interval for population mean
df =7 -1 = 6
t = 3.1427 from the t –distribution diagram above
= x ¿¿ = 7.0429¿ ¿)
98% CI = (6.4457, 7.6401)
b) H0: u = 7.5
Versus, H0 < 7.5
α =1 % level
Test statistic, t = x−u
sd / √n = 7.0429−7.5
0.5028/ √7
t = -2.4053
P-value = 0.0265
P-value > ∝
Tailed to reject H0
Question 8
n = 7, x= ∑ x
n = 49.3
7 =7.0429
s.d = √ 1
n−1 ¿ ¿
= √ 1
6 ¿ ¿ = 0.5028
a) 98% confidence interval for population mean
df =7 -1 = 6
t = 3.1427 from the t –distribution diagram above
= x ¿¿ = 7.0429¿ ¿)
98% CI = (6.4457, 7.6401)
b) H0: u = 7.5
Versus, H0 < 7.5
α =1 % level
Test statistic, t = x−u
sd / √n = 7.0429−7.5
0.5028/ √7
t = -2.4053
P-value = 0.0265
P-value > ∝
Tailed to reject H0
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

There is no evidence to support the claim that population less than 7.5
Question 8
a) P ( 0.5< x <2 )∨x ≤3
= P [ ( 0.5< x< 2 ) ∩ ( x ≤3 ) ]
p ( x ≤ 3)
= P [0.5< x< 2]
P( x ≤3)
=
∫
0.5
1
x
2 dx+∫
1
2
4−x
6 dx
∫
0
1
x
2 dx +∫
1
3
4−x
6 dx
= 1
4 ( 1−0.25 )+ 1
6 ¿ ¿
=
0.1875+2.5
6
1
4 + 4
6
= 0.6591
b) As Xi’s are iid random variables
E(T) = E¿i)
= 81 * E ¿i) = 5
3∗81=135
Var(T) = Var¿i)
= 812 * Var*Xi) = 812 * Var(x)
= 812*Var(Xi) = 812 * Var(x)
= 812 * 13/18
= 4738.56
As n = sample size = 81 > 70
So we use CLT
P(125 < T < 140) = P( 125−135
√ 4738.5 < T −135
√ 4738.5 < 140−135
√ 4738.5 )
T −135
√4738.5 =Z
¿ ф ( 0.073 )−ф(−0.145) N (0 , 1)
= 0.5291 – 0.4424
= 0.0867
Question 8
a) P ( 0.5< x <2 )∨x ≤3
= P [ ( 0.5< x< 2 ) ∩ ( x ≤3 ) ]
p ( x ≤ 3)
= P [0.5< x< 2]
P( x ≤3)
=
∫
0.5
1
x
2 dx+∫
1
2
4−x
6 dx
∫
0
1
x
2 dx +∫
1
3
4−x
6 dx
= 1
4 ( 1−0.25 )+ 1
6 ¿ ¿
=
0.1875+2.5
6
1
4 + 4
6
= 0.6591
b) As Xi’s are iid random variables
E(T) = E¿i)
= 81 * E ¿i) = 5
3∗81=135
Var(T) = Var¿i)
= 812 * Var*Xi) = 812 * Var(x)
= 812*Var(Xi) = 812 * Var(x)
= 812 * 13/18
= 4738.56
As n = sample size = 81 > 70
So we use CLT
P(125 < T < 140) = P( 125−135
√ 4738.5 < T −135
√ 4738.5 < 140−135
√ 4738.5 )
T −135
√4738.5 =Z
¿ ф ( 0.073 )−ф(−0.145) N (0 , 1)
= 0.5291 – 0.4424
= 0.0867
1 out of 8
Related Documents
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
© 2024 | Zucol Services PVT LTD | All rights reserved.





