Physics Questions and Answers | Acceleration and Mass
VerifiedAdded on 2022/09/07
|4
|648
|22
AI Summary
Contribute Materials
Your contribution can guide someone’s learning journey. Share your
documents today.

QUESTION 5
Q5A) substitute D operator for dy
dx ,: (aD2+bD+C)x=0
Substituting m for D: am2+ bm+C=0
m= −b ± √ b2−4 ac
2a but r = -b/2a and ω= √4 ac−b2
2 a hence, jω = √b2−4 ac
2 a ,since b2 ≠ 4ac
hence, m= r±jω, ( complex roots). Therefore x(t) = ert(C1cos ωt+ C2sin ωt).
Q5B) (aD2+K)x=0
Substituting C for D: mC2+K=0; C= ± √−k
m , Let C= ±jω (since the C is complex)
Therefore, x(t)= e0(Acos ωt + Bsin ωt); Hence x(t) = Acos ωt + Bsin ωt
Q5C) x(t) = 0Acos ωt + Bsin ωt
Assume the initial conditions: y(0) =4, dx
dt = 9,
At x(0) =4, 4=Acos 0 + Bsin 0 i.e. A=4……….(i)
dx
dx = -ωAsinωt+ Bcos ωt; 9= 0 + Bcos 0; B=9…...(ii)
Hence x(t)= 4cos ωt + 9 sin ωt
Let m=N7+1=3+1=4, and k= N8+1=9+1=10,
Hence, (4D2+10)X= 0;
Replacing D with C; 4C2+10=0; C= ± √ −10
4 = ± j 1.58
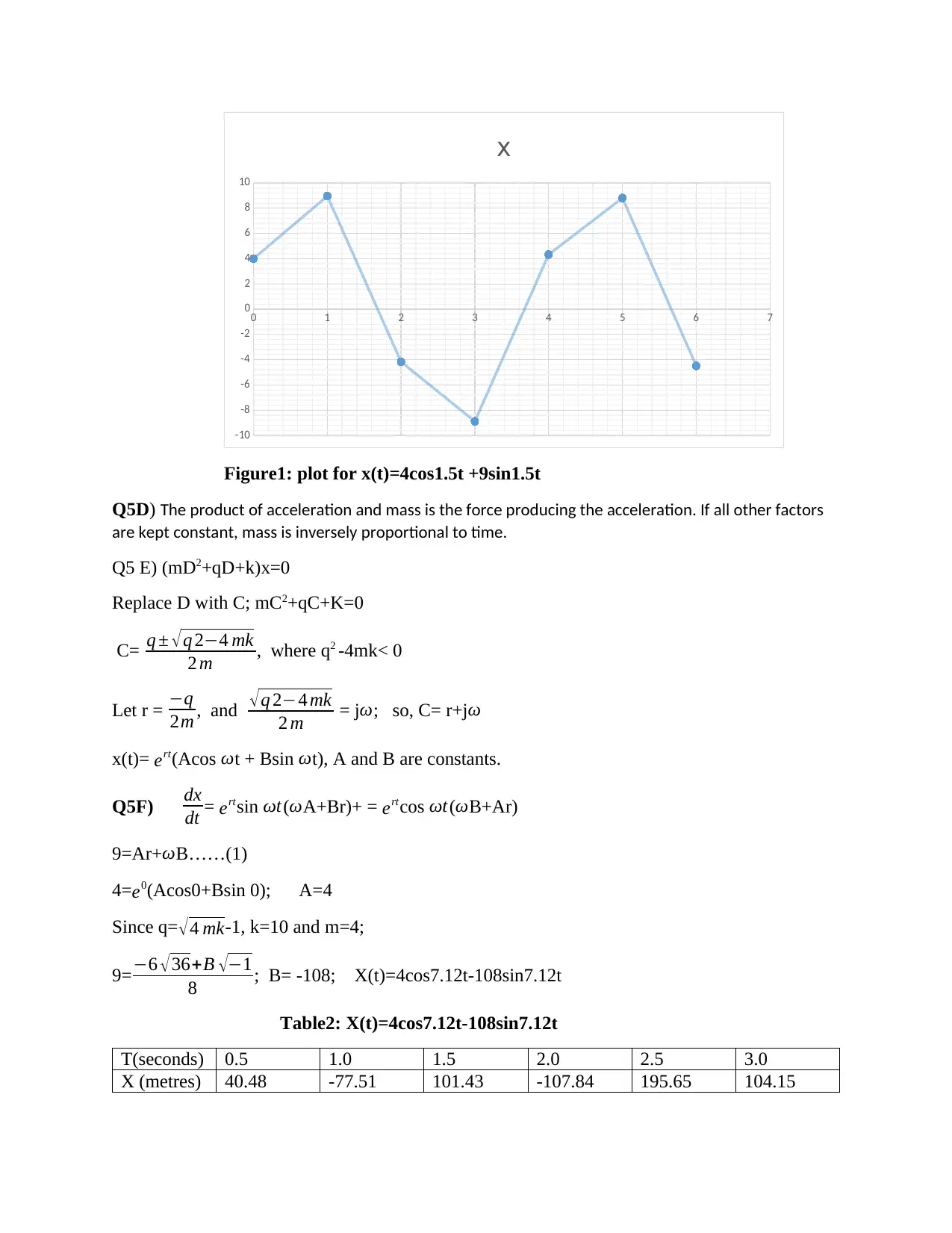
X(t)= 4cos 1.58t +9sin 1.58t
Table 1: X(t)=4cos 1.58t + 9sin 1.58t
t in
seconds(s)
0 1.0 2.0 3.0 4.0 5.0 6.0
X in
metres
(m)
4 8.96 -4.17 -8.89 4.33 8.81 -4.49
Q5A) substitute D operator for dy
dx ,: (aD2+bD+C)x=0
Substituting m for D: am2+ bm+C=0
m= −b ± √ b2−4 ac
2a but r = -b/2a and ω= √4 ac−b2
2 a hence, jω = √b2−4 ac
2 a ,since b2 ≠ 4ac
hence, m= r±jω, ( complex roots). Therefore x(t) = ert(C1cos ωt+ C2sin ωt).
Q5B) (aD2+K)x=0
Substituting C for D: mC2+K=0; C= ± √−k
m , Let C= ±jω (since the C is complex)
Therefore, x(t)= e0(Acos ωt + Bsin ωt); Hence x(t) = Acos ωt + Bsin ωt
Q5C) x(t) = 0Acos ωt + Bsin ωt
Assume the initial conditions: y(0) =4, dx
dt = 9,
At x(0) =4, 4=Acos 0 + Bsin 0 i.e. A=4……….(i)
dx
dx = -ωAsinωt+ Bcos ωt; 9= 0 + Bcos 0; B=9…...(ii)
Hence x(t)= 4cos ωt + 9 sin ωt
Let m=N7+1=3+1=4, and k= N8+1=9+1=10,
Hence, (4D2+10)X= 0;
Replacing D with C; 4C2+10=0; C= ± √ −10
4 = ± j 1.58
X(t)= 4cos 1.58t +9sin 1.58t
Table 1: X(t)=4cos 1.58t + 9sin 1.58t
t in
seconds(s)
0 1.0 2.0 3.0 4.0 5.0 6.0
X in
metres
(m)
4 8.96 -4.17 -8.89 4.33 8.81 -4.49
Secure Best Marks with AI Grader
Need help grading? Try our AI Grader for instant feedback on your assignments.
0 1 2 3 4 5 6 7
-10
-8
-6
-4
-2
0
2
4
6
8
10
x
Figure1: plot for x(t)=4cos1.5t +9sin1.5t
Q5D) The product of acceleration and mass is the force producing the acceleration. If all other factors
are kept constant, mass is inversely proportional to time.
Q5 E) (mD2+qD+k)x=0
Replace D with C; mC2+qC+K=0
C= q ± √q 2−4 mk
2 m , where q2 -4mk< 0
Let r = −q
2m , and √q 2−4 mk
2 m = jω; so, C= r+j ω
x(t)= ert(Acos ωt + Bsin ωt), A and B are constants.
Q5F) dx
dt = ertsin ωt (ωA+Br)+ = ertcos ωt(ωB+Ar)
9=Ar+ωB……(1)
4= e0(Acos0+Bsin 0); A=4
Since q= √4 mk-1, k=10 and m=4;
9=−6 √36+B √−1
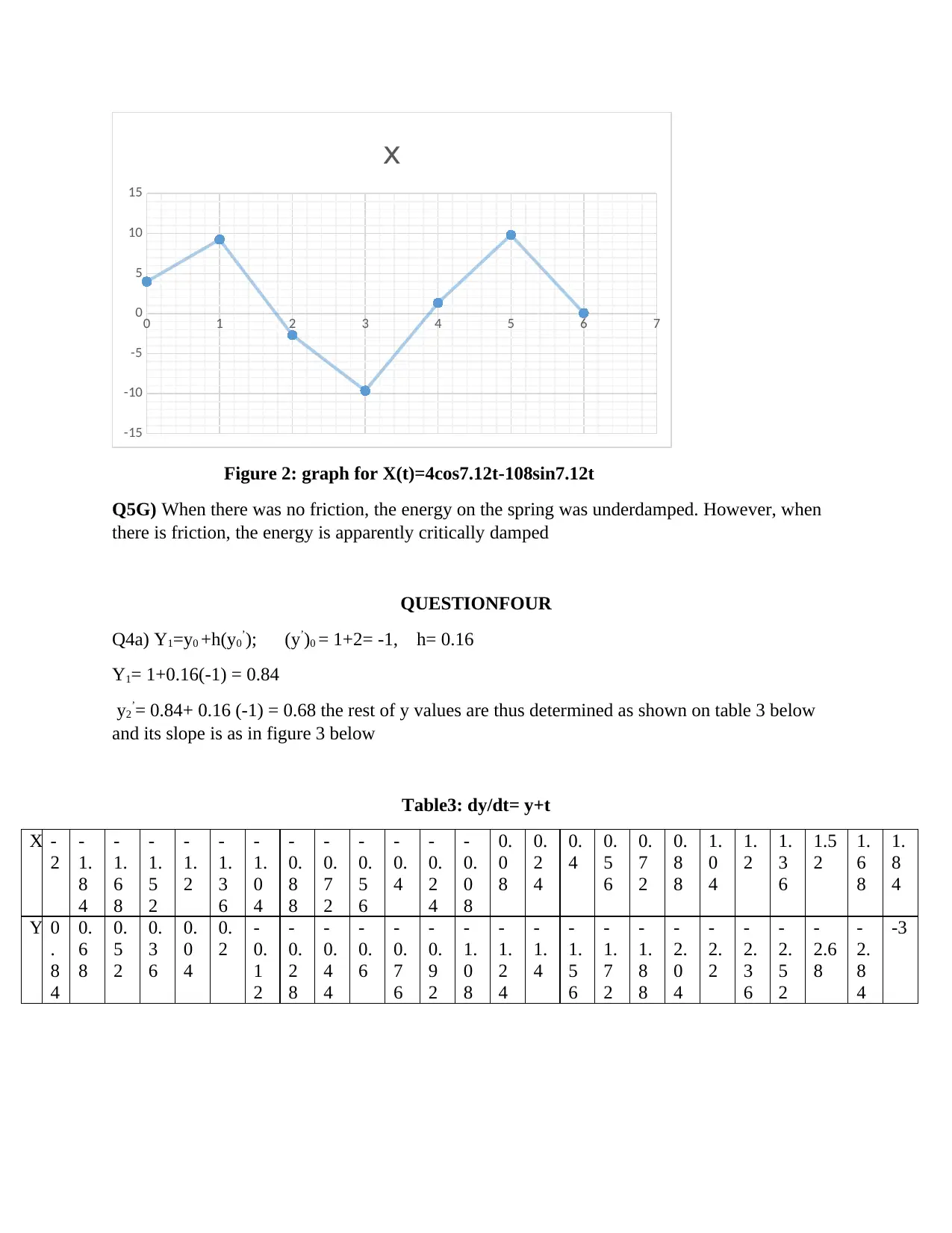
8 ; B= -108; X(t)=4cos7.12t-108sin7.12t
Table2: X(t)=4cos7.12t-108sin7.12t
T(seconds) 0.5 1.0 1.5 2.0 2.5 3.0
X (metres) 40.48 -77.51 101.43 -107.84 195.65 104.15
-10
-8
-6
-4
-2
0
2
4
6
8
10
x
Figure1: plot for x(t)=4cos1.5t +9sin1.5t
Q5D) The product of acceleration and mass is the force producing the acceleration. If all other factors
are kept constant, mass is inversely proportional to time.
Q5 E) (mD2+qD+k)x=0
Replace D with C; mC2+qC+K=0
C= q ± √q 2−4 mk
2 m , where q2 -4mk< 0
Let r = −q
2m , and √q 2−4 mk
2 m = jω; so, C= r+j ω
x(t)= ert(Acos ωt + Bsin ωt), A and B are constants.
Q5F) dx
dt = ertsin ωt (ωA+Br)+ = ertcos ωt(ωB+Ar)
9=Ar+ωB……(1)
4= e0(Acos0+Bsin 0); A=4
Since q= √4 mk-1, k=10 and m=4;
9=−6 √36+B √−1
8 ; B= -108; X(t)=4cos7.12t-108sin7.12t
Table2: X(t)=4cos7.12t-108sin7.12t
T(seconds) 0.5 1.0 1.5 2.0 2.5 3.0
X (metres) 40.48 -77.51 101.43 -107.84 195.65 104.15
0 1 2 3 4 5 6 7
-15
-10
-5
0
5
10
15
x
Figure 2: graph for X(t)=4cos7.12t-108sin7.12t
Q5G) When there was no friction, the energy on the spring was underdamped. However, when
there is friction, the energy is apparently critically damped
QUESTIONFOUR
Q4a) Y1=y0 +h(y0’); (y’)0 = 1+2= -1, h= 0.16
Y1= 1+0.16(-1) = 0.84
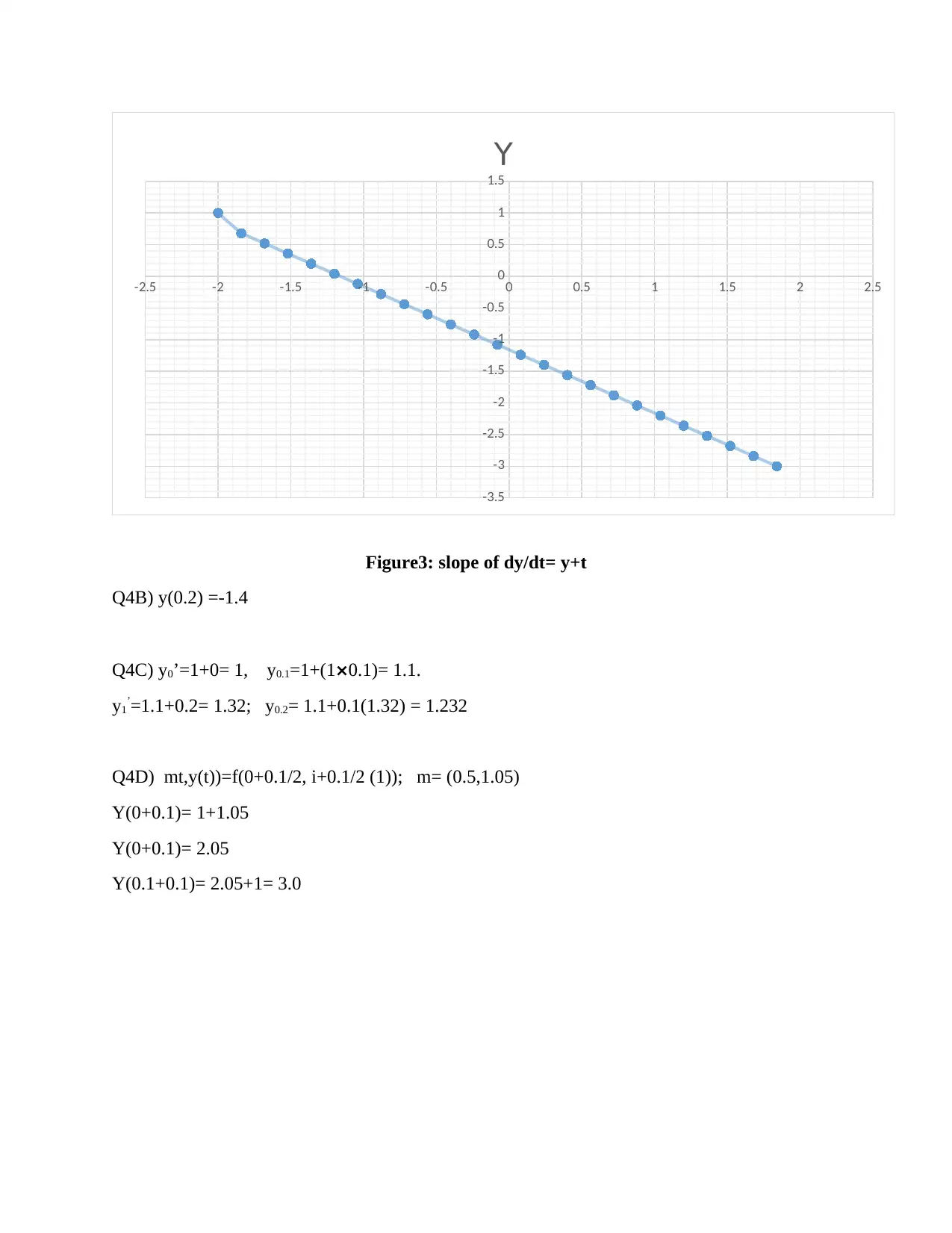
y2’= 0.84+ 0.16 (-1) = 0.68 the rest of y values are thus determined as shown on table 3 below
and its slope is as in figure 3 below
Table3: dy/dt= y+t
X -
2
-
1.
8
4
-
1.
6
8
-
1.
5
2
-
1.
2
-
1.
3
6
-
1.
0
4
-
0.
8
8
-
0.
7
2
-
0.
5
6
-
0.
4
-
0.
2
4
-
0.
0
8
0.
0
8
0.
2
4
0.
4
0.
5
6
0.
7
2
0.
8
8
1.
0
4
1.
2
1.
3
6
1.5
2
1.
6
8
1.
8
4
Y 0
.
8
4
0.
6
8
0.
5
2
0.
3
6
0.
0
4
0.
2
-
0.
1
2
-
0.
2
8
-
0.
4
4
-
0.
6
-
0.
7
6
-
0.
9
2
-
1.
0
8
-
1.
2
4
-
1.
4
-
1.
5
6
-
1.
7
2
-
1.
8
8
-
2.
0
4
-
2.
2
-
2.
3
6
-
2.
5
2
-
2.6
8
-
2.
8
4
-3
-15
-10
-5
0
5
10
15
x
Figure 2: graph for X(t)=4cos7.12t-108sin7.12t
Q5G) When there was no friction, the energy on the spring was underdamped. However, when
there is friction, the energy is apparently critically damped
QUESTIONFOUR
Q4a) Y1=y0 +h(y0’); (y’)0 = 1+2= -1, h= 0.16
Y1= 1+0.16(-1) = 0.84
y2’= 0.84+ 0.16 (-1) = 0.68 the rest of y values are thus determined as shown on table 3 below
and its slope is as in figure 3 below
Table3: dy/dt= y+t
X -
2
-
1.
8
4
-
1.
6
8
-
1.
5
2
-
1.
2
-
1.
3
6
-
1.
0
4
-
0.
8
8
-
0.
7
2
-
0.
5
6
-
0.
4
-
0.
2
4
-
0.
0
8
0.
0
8
0.
2
4
0.
4
0.
5
6
0.
7
2
0.
8
8
1.
0
4
1.
2
1.
3
6
1.5
2
1.
6
8
1.
8
4
Y 0
.
8
4
0.
6
8
0.
5
2
0.
3
6
0.
0
4
0.
2
-
0.
1
2
-
0.
2
8
-
0.
4
4
-
0.
6
-
0.
7
6
-
0.
9
2
-
1.
0
8
-
1.
2
4
-
1.
4
-
1.
5
6
-
1.
7
2
-
1.
8
8
-
2.
0
4
-
2.
2
-
2.
3
6
-
2.
5
2
-
2.6
8
-
2.
8
4
-3
-2.5 -2 -1.5 -1 -0.5 0 0.5 1 1.5 2 2.5
-3.5
-3
-2.5
-2
-1.5
-1
-0.5
0
0.5
1
1.5
Y
Figure3: slope of dy/dt= y+t
Q4B) y(0.2) =-1.4
Q4C) y0’=1+0= 1, y0.1=1+(1⨯0.1)= 1.1.
y1’=1.1+0.2= 1.32; y0.2= 1.1+0.1(1.32) = 1.232
Q4D) mt,y(t))=f(0+0.1/2, i+0.1/2 (1)); m= (0.5,1.05)
Y(0+0.1)= 1+1.05
Y(0+0.1)= 2.05
Y(0.1+0.1)= 2.05+1= 3.0
-3.5
-3
-2.5
-2
-1.5
-1
-0.5
0
0.5
1
1.5
Y
Figure3: slope of dy/dt= y+t
Q4B) y(0.2) =-1.4
Q4C) y0’=1+0= 1, y0.1=1+(1⨯0.1)= 1.1.
y1’=1.1+0.2= 1.32; y0.2= 1.1+0.1(1.32) = 1.232
Q4D) mt,y(t))=f(0+0.1/2, i+0.1/2 (1)); m= (0.5,1.05)
Y(0+0.1)= 1+1.05
Y(0+0.1)= 2.05
Y(0.1+0.1)= 2.05+1= 3.0
1 out of 4
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
© 2024 | Zucol Services PVT LTD | All rights reserved.

