ECTE962 Assignment: Optimizing Road Traffic Using Queuing Theory

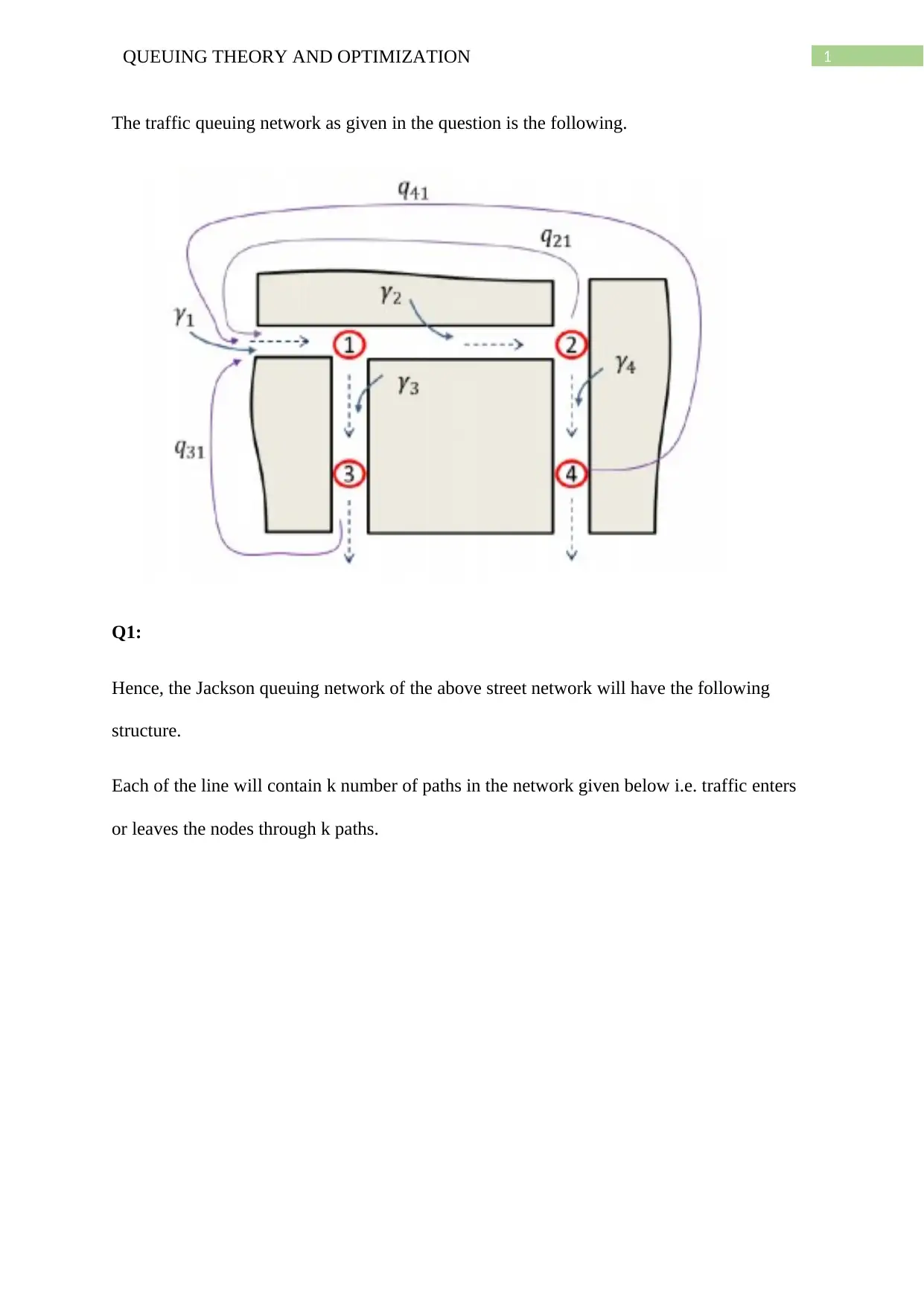
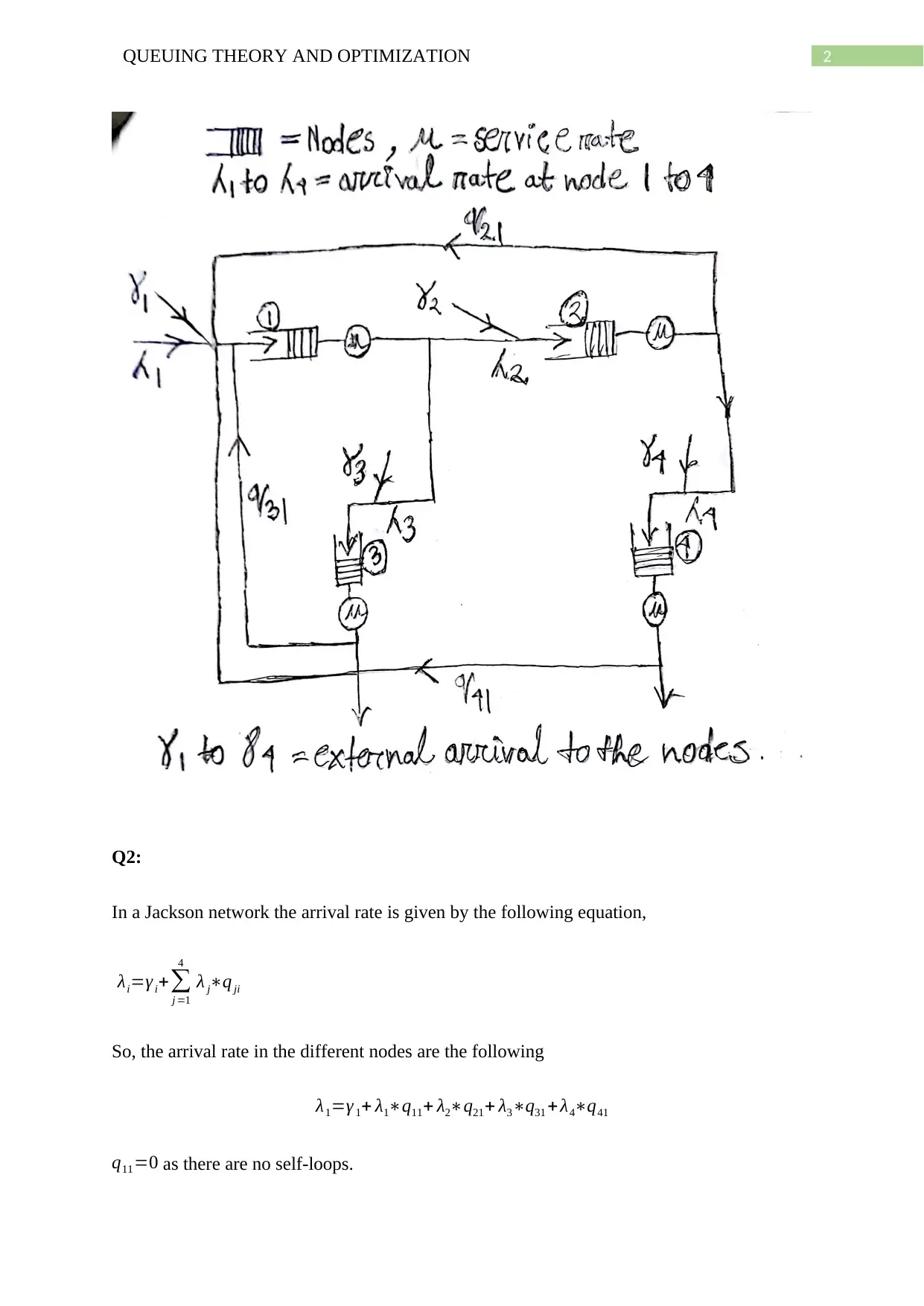
This assignment focuses on applying queuing theory to optimize road traffic networks. It analyzes a given traffic network using the Jackson queuing network model to determine arrival rates, individual delays, and total average delay. The assignment includes calculations using MATLAB to simulate traffic flow and optimize the number of lanes required to minimize congestion, considering factors like service rates and traffic distribution. The solution discusses the assumptions made, such as equal traffic distribution across paths and arrival rates being less than service rates, and provides a steady-state analysis of the network's performance. The goal is to determine the optimal road width (number of lanes) to manage traffic efficiently and reduce delays. Desklib offers solved assignments and resources for students.

Running head: QUEUING THEORY AND OPTIMIZATION
QUEUING THEORY AND OPTIMIZATION
Name of the Student
Name of the University
Author Note

1QUEUING THEORY AND OPTIMIZATION
The traffic queuing network as given in the question is the following.
Q1:
Hence, the Jackson queuing network of the above street network will have the following
structure.
Each of the line will contain k number of paths in the network given below i.e. traffic enters
or leaves the nodes through k paths.

2QUEUING THEORY AND OPTIMIZATION
Q2:
In a Jackson network the arrival rate is given by the following equation,
λi=γ i+∑
j =1
4
λ j∗q ji
So, the arrival rate in the different nodes are the following
λ1=γ 1+ λ1∗q11+ λ2∗q21+ λ3∗q31 + λ4∗q41
q11=0 as there are no self-loops.

3QUEUING THEORY AND OPTIMIZATION
Hence, the expression of λ1 is
λ1=γ 1+ λ2∗q21+ λ3∗q31 + λ4∗q41
Similarly, the expressions of λ2 , λ3 and λ4 are
λ2=γ 2+ λ1∗q12+ λ3∗q32 + λ4∗q42
λ3=γ 3 + λ1∗q13 + λ2∗q23 + λ4∗q43
λ4=γ 4 + λ1∗q14 +λ2∗q24+ λ3∗q34
Q3:
The individual delays Wi are given by,
Wi= 1
μi−λi
Where, μi = service rate of the ith node = μ for every node in this particular case.
λiis the arrival rate at the ith node where, i = 1 to 4.
Hence, the total average delay will be,
W = ∑
i=1
4
( λi
γN ¿)Wi ¿
Where, γN=¿ ∑
i=1
4
γi
Q4:
Now, the above expression of W = ∑
i=1
4
( λi
γN ¿)Wi ¿is for M/M/1 network where the number of
paths or lanes is 1 and when the number of paths are increased it is evident from the equation
that the individual delays Wi will decrease with the increase of the service rate μ and the total

4QUEUING THEORY AND OPTIMIZATION
average delay W will also decrease as Wi is in the numerator of the expression. This supports
the natural phenomenon also as increasing the number of paths in a network, traffic will have
more space to move and the congestion delay will be decreased.
Q5:
Given that, 𝛾𝑖=2 which is constant for all nodes from 1 to 4.
𝜇=8,q21=𝑞31=𝑞41=0.2,𝑞12=𝑞13=0.5 and 𝑘=3 for all nodes.
So, the Q matrix is Qij =
[ 0 0.5 0.5
0.2 0 0
0.2 0 0
0
0
0
¿ 0.2 0 0 0 ]
Now, as the network is an open network and it is assumed that the arrival rate
λi less than service rate ¿𝜇) hence, by Jackson’s theorem λi can be computed as,
λ=γ ( I −Q )−1
Now, as the number of paths k = 3 and hence, the external arrivals will be divided by 3.
Hence, the equation becomes,
λ=(γ /3) ¿ ( I −Q )−1
Now, in MATLAB the λ matrix (λ 1 ¿ λ 4 ¿ is calculated and by using those values the total
average delay has been calculated by the corresponding expressions of them as given above.
MATLAB code:
miu = 8; % constant service rate
gamma = [2,2,2,2]./3; % external arivals are divided by number of paths
Q =[0 0.5 0.5 0;0.2 0 0 0;0.2 0 0 0;0.2 0 0 0]; % qij probability matrix
I = eye(4); % identity matrix of order 4
lambda = gamma*((I-Q)^(-1)) % matrix of the arrival rates

5QUEUING THEORY AND OPTIMIZATION
w = zeros(4,1);
for i=1:4
w(i,1) = 1/(miu- lambda(1,i)); % individual delays at node i
end
w
TAVGW=0;
for i=1:4
TAVGW = TAVGW + (lambda(1,i)*w(i,1))/sum(gamma); % calculating total average delay
end
sprintf('the total average delay is %d',TAVGW)
Output:
lambda =
1.3333 1.3333 1.3333 0.6667
w =
0.1500
0.1500
0.1500
0.1364
ans =
'the total average delay is 2.590909e-01'
Now, the assumption that is made in the calculation is that it is presumed that the traffic is
equally distributed in k paths (where k=3) and hence, the external arrival rates are also

6QUEUING THEORY AND OPTIMIZATION
equally distributed in k paths. Also, it is assumed that arrival rates in each node is less than
the service rate as stated above.
So, in steady state the arrival rate matrix is λ = [1.3333 1.3333 1.3333 0.6667], the
individual delay matrix is
Wi = 0.1500
0.1500
0.1500
0.1364
So, the total average delay in the network in steady state as calculated above is W = 0.259 sec
or 259 msec.
Q6:
Now, in the steady state solution the ‘Rate in’ to any node is exactly equal to ‘Rate out’ from
that particular node. Now, for k=1 i.e. through a single path of traffic flow in the network the
service rate 𝜇 in each node must be more than the arrival rates in order to become the
individual delay time must be positive.
Now, for three lanes the arrivals rates are λ = [1.3333 1.3333 1.3333 0.6667].
Hence, for k= 1 the arrivals rates at the nodes 1 to 4 will be
3∗λ = [4 4 4 2]
Hence, the service rate 𝜇 must be greater than 4 in the steady state condition.

7QUEUING THEORY AND OPTIMIZATION