Quiz 4: Solve Math Problems and Equations
VerifiedAdded on 2022/10/12
|5
|762
|297
AI Summary
Quiz 4 includes solving math problems and equations related to algebra, quadratic formula, distance, product, and graph equations. Get step-by-step solutions to all the problems.
Contribute Materials
Your contribution can guide someone’s learning journey. Share your
documents today.

Quiz 4: Instructions:
1. -3(4x – 2) – 2(5x – 4)
Opening the bracket, multiply whatever is inside the bracket with what is outside to get,
-12x+6-10x+8.
Nb. Negative sign multiplied by a negative sign becomes a positive
Taking like terms together, the answer becomes
-22x+14
2. 6p +2= p2 + 3p3
3p3+ p2 - 6p – 2=0
p2 (3p+1) -2(3p+1) =0
(3p+1)(p2 -2) =0
P= - 1
3
P= ± 1.4142
3. (2 y) 4 = 3(2 y) 2 + 1
16 y4 −12 y2 −1=0
If y2= x then
16 x2−12 x −1=0
X=0.8256
X= -0.0757
Since x= y2
Then y= ±0.9086
4. z4 + 3z2 – 1 = 0
Let z2=x
x2+ 3 x −1=0
X= 0.3027
X= -3.302
So,
Z= ± 0.55018
5. √(25)(4)
=5*4=20
1. -3(4x – 2) – 2(5x – 4)
Opening the bracket, multiply whatever is inside the bracket with what is outside to get,
-12x+6-10x+8.
Nb. Negative sign multiplied by a negative sign becomes a positive
Taking like terms together, the answer becomes
-22x+14
2. 6p +2= p2 + 3p3
3p3+ p2 - 6p – 2=0
p2 (3p+1) -2(3p+1) =0
(3p+1)(p2 -2) =0
P= - 1
3
P= ± 1.4142
3. (2 y) 4 = 3(2 y) 2 + 1
16 y4 −12 y2 −1=0
If y2= x then
16 x2−12 x −1=0
X=0.8256
X= -0.0757
Since x= y2
Then y= ±0.9086
4. z4 + 3z2 – 1 = 0
Let z2=x
x2+ 3 x −1=0
X= 0.3027
X= -3.302
So,
Z= ± 0.55018
5. √(25)(4)
=5*4=20
Secure Best Marks with AI Grader
Need help grading? Try our AI Grader for instant feedback on your assignments.

Nb. The square root only covers 25 not the whole quantity as indicated by the bracket.
6.
f(x) = x 2 + 2
-2.5 -2 -1.5 -1 -0.5 0 0.5 1 1.5 2 2.5
0
1
2
3
4
5
6
7
f(x)=x^2 +2
x
f(x)
From the graph range =∞
7. |2x + 1| − 5 < 0
2x+1 < 5
2x < 4
X< 2
The solution is (2)
8. |x + 3| ≥ |6x + 9|
-6 ≥ 5x
x≤1.2
The solution is [1.2]
9.
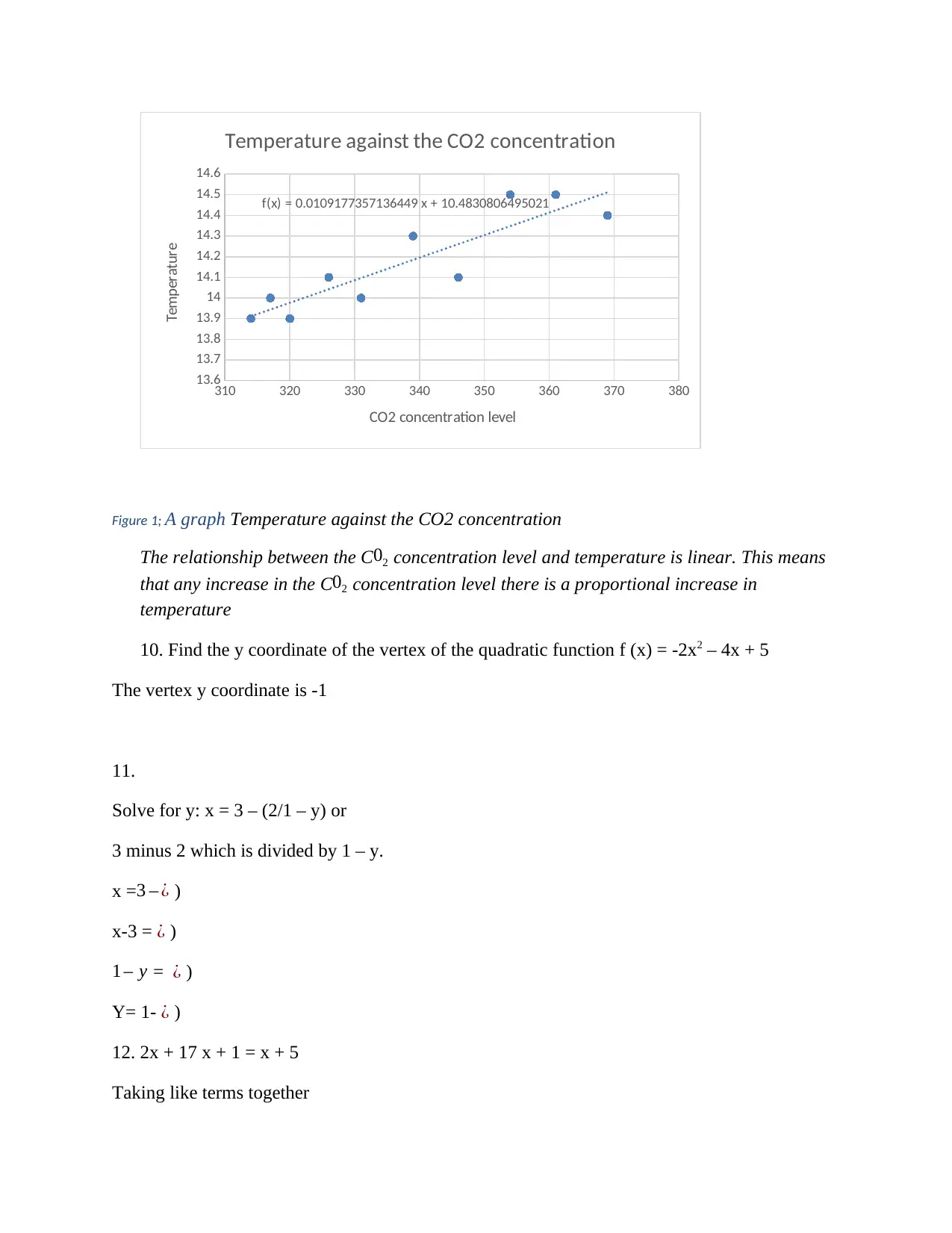
CO2 314 317 320 326 331 339 346 354 361 369
Temp 13.9 14.0 13.9 14.1 14.0 14.3 14.1 14.5 14.5 14.4
6.
f(x) = x 2 + 2
-2.5 -2 -1.5 -1 -0.5 0 0.5 1 1.5 2 2.5
0
1
2
3
4
5
6
7
f(x)=x^2 +2
x
f(x)
From the graph range =∞
7. |2x + 1| − 5 < 0
2x+1 < 5
2x < 4
X< 2
The solution is (2)
8. |x + 3| ≥ |6x + 9|
-6 ≥ 5x
x≤1.2
The solution is [1.2]
9.
CO2 314 317 320 326 331 339 346 354 361 369
Temp 13.9 14.0 13.9 14.1 14.0 14.3 14.1 14.5 14.5 14.4
310 320 330 340 350 360 370 380
13.6
13.7
13.8
13.9
14
14.1
14.2
14.3
14.4
14.5
14.6
f(x) = 0.0109177357136449 x + 10.4830806495021
Temperature against the CO2 concentration
CO2 concentration level
Temperature
Figure 1; A graph Temperature against the CO2 concentration
The relationship between the C02 concentration level and temperature is linear. This means
that any increase in the C02 concentration level there is a proportional increase in
temperature
10. Find the y coordinate of the vertex of the quadratic function f (x) = -2x2 – 4x + 5
The vertex y coordinate is -1
11.
Solve for y: x = 3 – (2/1 – y) or
3 minus 2 which is divided by 1 – y.
x =3 – ¿ )
x-3 = ¿ )
1 – y = ¿ )
Y= 1- ¿ )
12. 2x + 17 x + 1 = x + 5
Taking like terms together
13.6
13.7
13.8
13.9
14
14.1
14.2
14.3
14.4
14.5
14.6
f(x) = 0.0109177357136449 x + 10.4830806495021
Temperature against the CO2 concentration
CO2 concentration level
Temperature
Figure 1; A graph Temperature against the CO2 concentration
The relationship between the C02 concentration level and temperature is linear. This means
that any increase in the C02 concentration level there is a proportional increase in
temperature
10. Find the y coordinate of the vertex of the quadratic function f (x) = -2x2 – 4x + 5
The vertex y coordinate is -1
11.
Solve for y: x = 3 – (2/1 – y) or
3 minus 2 which is divided by 1 – y.
x =3 – ¿ )
x-3 = ¿ )
1 – y = ¿ )
Y= 1- ¿ )
12. 2x + 17 x + 1 = x + 5
Taking like terms together

18x=4
Making x the subject of the formula x= 4
18 = 2
9
13. The quadratic formula states: x=−b ± √ b2−4 ac
2 a
Given, a=2 b=2 c=-3
Therefore, the equation becomes x=−2 ± √22−(4∗2∗−3¿)
2∗2 ¿=¿ −2± √26
4
14. Distance between (-2, 3) and (4, -5)
-2 and 4 are the x values while 3 and -5 y values.
Therefore, the distances from these values are (6, 8)
From Pythagoras theorem, the distance between them will be √ 82 +62=√100=10
15. The sum of 2z2 + z + 5 and 4z2 + 3z + 1 is
Nb. Additions is only done for like terms
6z2 + 4z + 6
16. The product of x - 1 and 2x2 - x - 1 is
Opening the bracket, multiply whatever is inside the bracket with what is outside to get,
2x3-x2-x-2x2+x+1
Nb. Negative sign multiplied by a negative sign becomes a positive answer
Negative sign multiplied by a positive sign give a negative answer
Taking like terms together, the answer becomes
2x3-3x2+1
17. Solve 3(x - 2) - 4(2 + 3x) = x + 10
Opening the bracket, multiply whatever is inside the bracket with what is outside to get,
3x-6-8-12x=x+10
Making x the subject of the formula x= 4
18 = 2
9
13. The quadratic formula states: x=−b ± √ b2−4 ac
2 a
Given, a=2 b=2 c=-3
Therefore, the equation becomes x=−2 ± √22−(4∗2∗−3¿)
2∗2 ¿=¿ −2± √26
4
14. Distance between (-2, 3) and (4, -5)
-2 and 4 are the x values while 3 and -5 y values.
Therefore, the distances from these values are (6, 8)
From Pythagoras theorem, the distance between them will be √ 82 +62=√100=10
15. The sum of 2z2 + z + 5 and 4z2 + 3z + 1 is
Nb. Additions is only done for like terms
6z2 + 4z + 6
16. The product of x - 1 and 2x2 - x - 1 is
Opening the bracket, multiply whatever is inside the bracket with what is outside to get,
2x3-x2-x-2x2+x+1
Nb. Negative sign multiplied by a negative sign becomes a positive answer
Negative sign multiplied by a positive sign give a negative answer
Taking like terms together, the answer becomes
2x3-3x2+1
17. Solve 3(x - 2) - 4(2 + 3x) = x + 10
Opening the bracket, multiply whatever is inside the bracket with what is outside to get,
3x-6-8-12x=x+10
Secure Best Marks with AI Grader
Need help grading? Try our AI Grader for instant feedback on your assignments.

Nb. Negative sign multiplied by a negative sign becomes a positive
Taking like terms together, the answer becomes
10x=-24
Simplifying this the answer becomes
X=-24
10 =- 12
5
18. (4 - 5x)(3 + 25x) =
Opening the bracket, multiply whatever is inside the bracket with what is outside to get,
12+100x-15x-125x2
Nb. Negative sign multiplied by a positive sign becomes a negative
Taking like terms together, the answer becomes
12-85x-125x2
19. This is the graph of which equation?
The equation is of the form, y=mx+c where m is the gradient of the line and c is the y intercept,
or where the line cuts the y axis.
In this case, the line cuts the y intercept at 1. The gradient is calculated as Δ y
Δ x = 3−1
1−0 =2
Therefore, the equation of the line is y=2x+1
20. Let f(x) = -x² - 3x + 4, then f (-2) =
f(2) = -(2)² - 3(2) + 4,
= -4 -6 +4
= -6
Taking like terms together, the answer becomes
10x=-24
Simplifying this the answer becomes
X=-24
10 =- 12
5
18. (4 - 5x)(3 + 25x) =
Opening the bracket, multiply whatever is inside the bracket with what is outside to get,
12+100x-15x-125x2
Nb. Negative sign multiplied by a positive sign becomes a negative
Taking like terms together, the answer becomes
12-85x-125x2
19. This is the graph of which equation?
The equation is of the form, y=mx+c where m is the gradient of the line and c is the y intercept,
or where the line cuts the y axis.
In this case, the line cuts the y intercept at 1. The gradient is calculated as Δ y
Δ x = 3−1
1−0 =2
Therefore, the equation of the line is y=2x+1
20. Let f(x) = -x² - 3x + 4, then f (-2) =
f(2) = -(2)² - 3(2) + 4,
= -4 -6 +4
= -6
1 out of 5
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
© 2024 | Zucol Services PVT LTD | All rights reserved.