Regression Models: Analyzing Car Sale Prices Using Regression Analysis
VerifiedAdded on 2023/06/07
|11
|1789
|244
Report
AI Summary
This report analyzes car sale prices using various regression models, incorporating factors like length and weight. Descriptive statistics are presented for sale price, length, and weight, followed by estimations of simple regression models, including a log-log specification. The report examines the impact of length and weight on sale price, tests the significance of these variables, and explores the effects of adding horsepower and luggage size to the model. Hypothesis testing is conducted to determine if luxury cars are more expensive. The overall significance of the models is assessed using significance F values and P-values to determine the statistical significance of the variables. The report concludes with a discussion of the findings and their implications for understanding the factors influencing car sale prices. Desklib provides access to similar solved assignments for students.

Regression Models
Regression Model Assignment
Student’s Name
Institution Affiliation
Regression Model Assignment
Student’s Name
Institution Affiliation
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
Regression Models
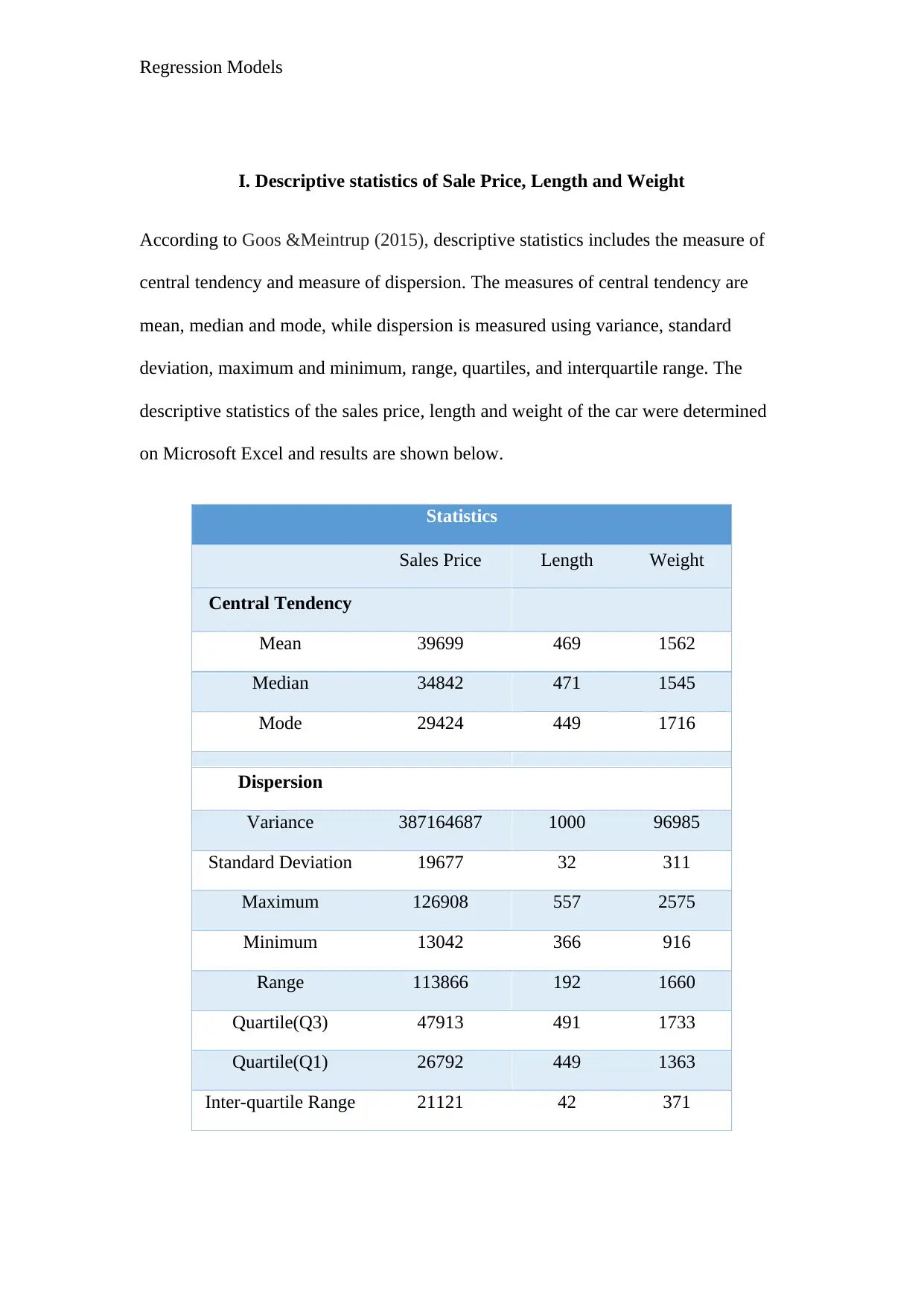
I. Descriptive statistics of Sale Price, Length and Weight
According to Goos &Meintrup (2015), descriptive statistics includes the measure of
central tendency and measure of dispersion. The measures of central tendency are
mean, median and mode, while dispersion is measured using variance, standard
deviation, maximum and minimum, range, quartiles, and interquartile range. The
descriptive statistics of the sales price, length and weight of the car were determined
on Microsoft Excel and results are shown below.
Statistics
Sales Price Length Weight
Central Tendency
Mean 39699 469 1562
Median 34842 471 1545
Mode 29424 449 1716
Dispersion
Variance 387164687 1000 96985
Standard Deviation 19677 32 311
Maximum 126908 557 2575
Minimum 13042 366 916
Range 113866 192 1660
Quartile(Q3) 47913 491 1733
Quartile(Q1) 26792 449 1363
Inter-quartile Range 21121 42 371
I. Descriptive statistics of Sale Price, Length and Weight
According to Goos &Meintrup (2015), descriptive statistics includes the measure of
central tendency and measure of dispersion. The measures of central tendency are
mean, median and mode, while dispersion is measured using variance, standard
deviation, maximum and minimum, range, quartiles, and interquartile range. The
descriptive statistics of the sales price, length and weight of the car were determined
on Microsoft Excel and results are shown below.
Statistics
Sales Price Length Weight
Central Tendency
Mean 39699 469 1562
Median 34842 471 1545
Mode 29424 449 1716
Dispersion
Variance 387164687 1000 96985
Standard Deviation 19677 32 311
Maximum 126908 557 2575
Minimum 13042 366 916
Range 113866 192 1660
Quartile(Q3) 47913 491 1733
Quartile(Q1) 26792 449 1363
Inter-quartile Range 21121 42 371

Regression Models
The mean is greater than the median, which is greater than the mode for the three
variables. This indicates that the distributions for the three are positively skewed
(Sharma 2007; Data& Using Descriptive Statistics Bartz 1988). The variances and
standard deviations of the three variables are very high. Higher variance and standard
is an indicator of much-dispersed data points from the mean (Bernstein& Bernstein
1998). According to Brase& Brase (2011), a big range indicates a greater dispersion
of data points, whereas a small range shows a less dispersion. Comparing the three
variables, sales price has the biggest range and interquartile range, what makes its
data to have the greatest dispersion among the three.
II. Estimation of a simple regression model of the Sale price on Length,
Sale Price=β0 +β1 length+u
The values of β0 and β1 were determine using Microsoft Excel, regression analysis.
The results are shown below.
SUMMARY OUTPUT
Regression Statistics
The mean is greater than the median, which is greater than the mode for the three
variables. This indicates that the distributions for the three are positively skewed
(Sharma 2007; Data& Using Descriptive Statistics Bartz 1988). The variances and
standard deviations of the three variables are very high. Higher variance and standard
is an indicator of much-dispersed data points from the mean (Bernstein& Bernstein
1998). According to Brase& Brase (2011), a big range indicates a greater dispersion
of data points, whereas a small range shows a less dispersion. Comparing the three
variables, sales price has the biggest range and interquartile range, what makes its
data to have the greatest dispersion among the three.
II. Estimation of a simple regression model of the Sale price on Length,
Sale Price=β0 +β1 length+u
The values of β0 and β1 were determine using Microsoft Excel, regression analysis.
The results are shown below.
SUMMARY OUTPUT
Regression Statistics
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
Regression Models
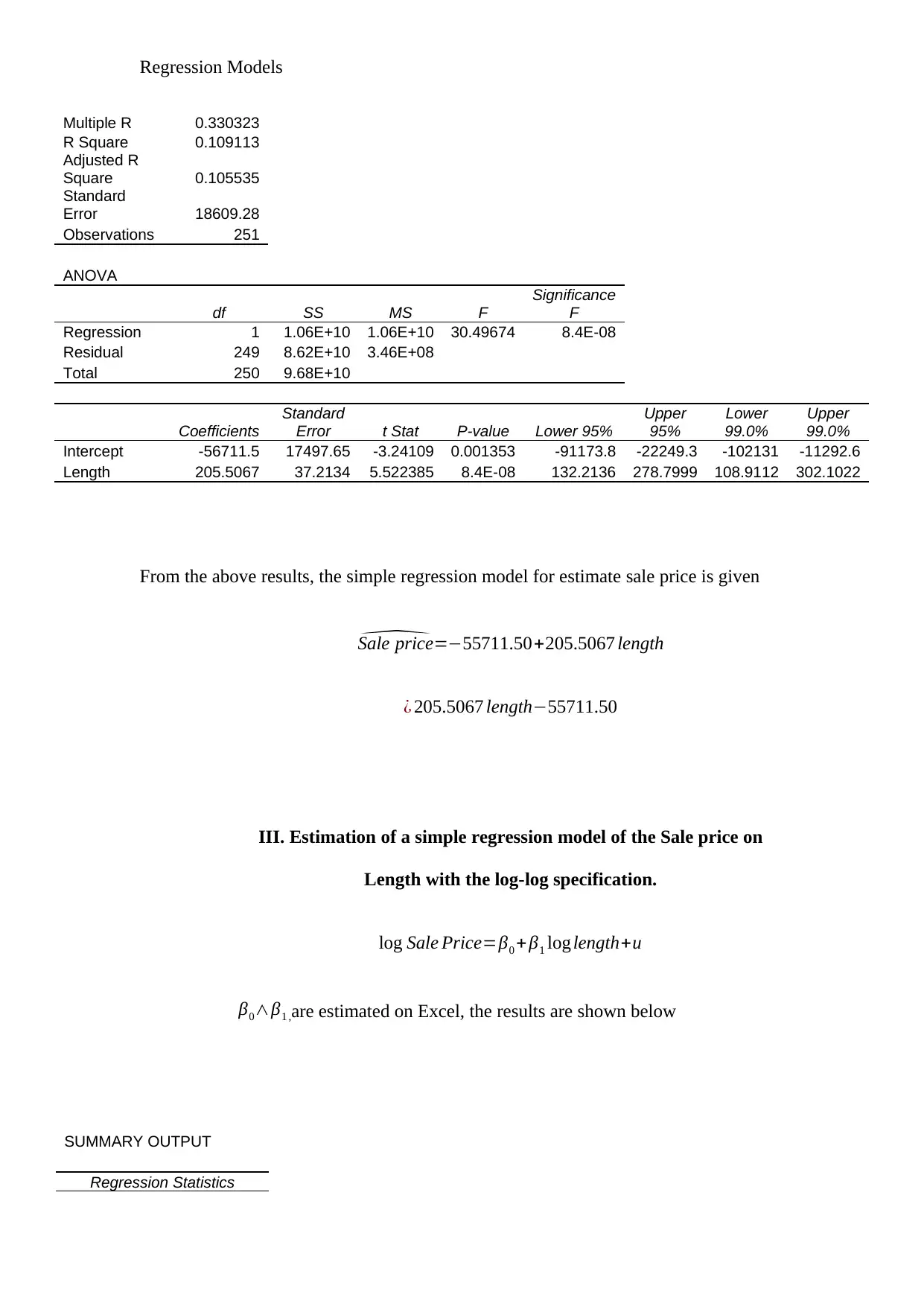
Multiple R 0.330323
R Square 0.109113
Adjusted R
Square 0.105535
Standard
Error 18609.28
Observations 251
ANOVA
df SS MS F
Significance
F
Regression 1 1.06E+10 1.06E+10 30.49674 8.4E-08
Residual 249 8.62E+10 3.46E+08
Total 250 9.68E+10
Coefficients
Standard
Error t Stat P-value Lower 95%
Upper
95%
Lower
99.0%
Upper
99.0%
Intercept -56711.5 17497.65 -3.24109 0.001353 -91173.8 -22249.3 -102131 -11292.6
Length 205.5067 37.2134 5.522385 8.4E-08 132.2136 278.7999 108.9112 302.1022
From the above results, the simple regression model for estimate sale price is given
^Sale price=−55711.50+205.5067 length
¿ 205.5067 length−55711.50
III. Estimation of a simple regression model of the Sale price on
Length with the log-log specification.
log Sale Price=β0 + β1 log length+u
β0∧β1 ,are estimated on Excel, the results are shown below
SUMMARY OUTPUT
Regression Statistics
Multiple R 0.330323
R Square 0.109113
Adjusted R
Square 0.105535
Standard
Error 18609.28
Observations 251
ANOVA
df SS MS F
Significance
F
Regression 1 1.06E+10 1.06E+10 30.49674 8.4E-08
Residual 249 8.62E+10 3.46E+08
Total 250 9.68E+10
Coefficients
Standard
Error t Stat P-value Lower 95%
Upper
95%
Lower
99.0%
Upper
99.0%
Intercept -56711.5 17497.65 -3.24109 0.001353 -91173.8 -22249.3 -102131 -11292.6
Length 205.5067 37.2134 5.522385 8.4E-08 132.2136 278.7999 108.9112 302.1022
From the above results, the simple regression model for estimate sale price is given
^Sale price=−55711.50+205.5067 length
¿ 205.5067 length−55711.50
III. Estimation of a simple regression model of the Sale price on
Length with the log-log specification.
log Sale Price=β0 + β1 log length+u
β0∧β1 ,are estimated on Excel, the results are shown below
SUMMARY OUTPUT
Regression Statistics
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
Regression Models
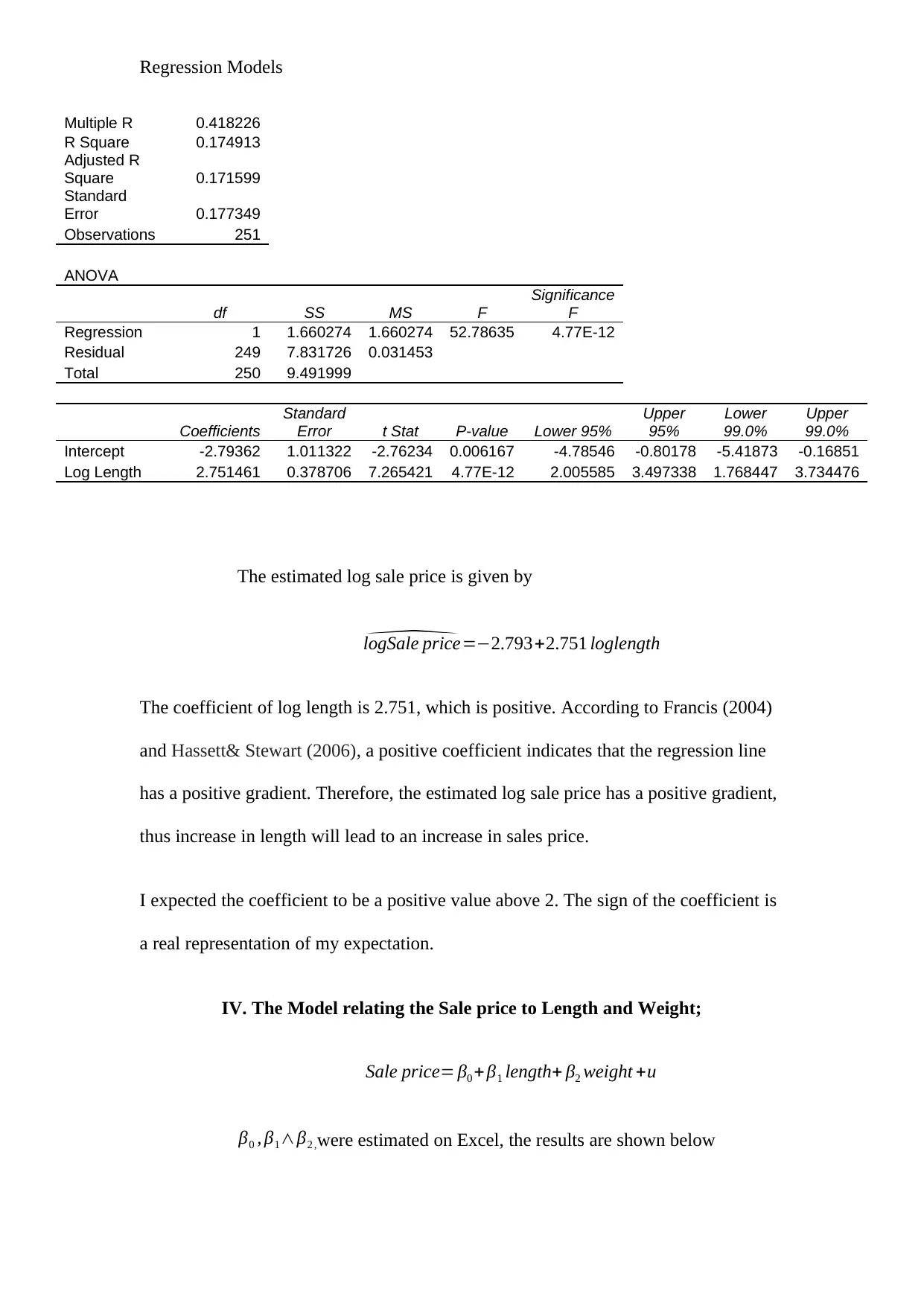
Multiple R 0.418226
R Square 0.174913
Adjusted R
Square 0.171599
Standard
Error 0.177349
Observations 251
ANOVA
df SS MS F
Significance
F
Regression 1 1.660274 1.660274 52.78635 4.77E-12
Residual 249 7.831726 0.031453
Total 250 9.491999
Coefficients
Standard
Error t Stat P-value Lower 95%
Upper
95%
Lower
99.0%
Upper
99.0%
Intercept -2.79362 1.011322 -2.76234 0.006167 -4.78546 -0.80178 -5.41873 -0.16851
Log Length 2.751461 0.378706 7.265421 4.77E-12 2.005585 3.497338 1.768447 3.734476
The estimated log sale price is given by
^logSale price=−2.793+2.751 loglength
The coefficient of log length is 2.751, which is positive. According to Francis (2004)
and Hassett& Stewart (2006), a positive coefficient indicates that the regression line
has a positive gradient. Therefore, the estimated log sale price has a positive gradient,
thus increase in length will lead to an increase in sales price.
I expected the coefficient to be a positive value above 2. The sign of the coefficient is
a real representation of my expectation.
IV. The Model relating the Sale price to Length and Weight;
Sale price= β0 + β1 length+ β2 weight +u
β0 , β1∧β2 ,were estimated on Excel, the results are shown below
Multiple R 0.418226
R Square 0.174913
Adjusted R
Square 0.171599
Standard
Error 0.177349
Observations 251
ANOVA
df SS MS F
Significance
F
Regression 1 1.660274 1.660274 52.78635 4.77E-12
Residual 249 7.831726 0.031453
Total 250 9.491999
Coefficients
Standard
Error t Stat P-value Lower 95%
Upper
95%
Lower
99.0%
Upper
99.0%
Intercept -2.79362 1.011322 -2.76234 0.006167 -4.78546 -0.80178 -5.41873 -0.16851
Log Length 2.751461 0.378706 7.265421 4.77E-12 2.005585 3.497338 1.768447 3.734476
The estimated log sale price is given by
^logSale price=−2.793+2.751 loglength
The coefficient of log length is 2.751, which is positive. According to Francis (2004)
and Hassett& Stewart (2006), a positive coefficient indicates that the regression line
has a positive gradient. Therefore, the estimated log sale price has a positive gradient,
thus increase in length will lead to an increase in sales price.
I expected the coefficient to be a positive value above 2. The sign of the coefficient is
a real representation of my expectation.
IV. The Model relating the Sale price to Length and Weight;
Sale price= β0 + β1 length+ β2 weight +u
β0 , β1∧β2 ,were estimated on Excel, the results are shown below
Regression Models
SUMMARY
OUTPUT
Regression Statistics
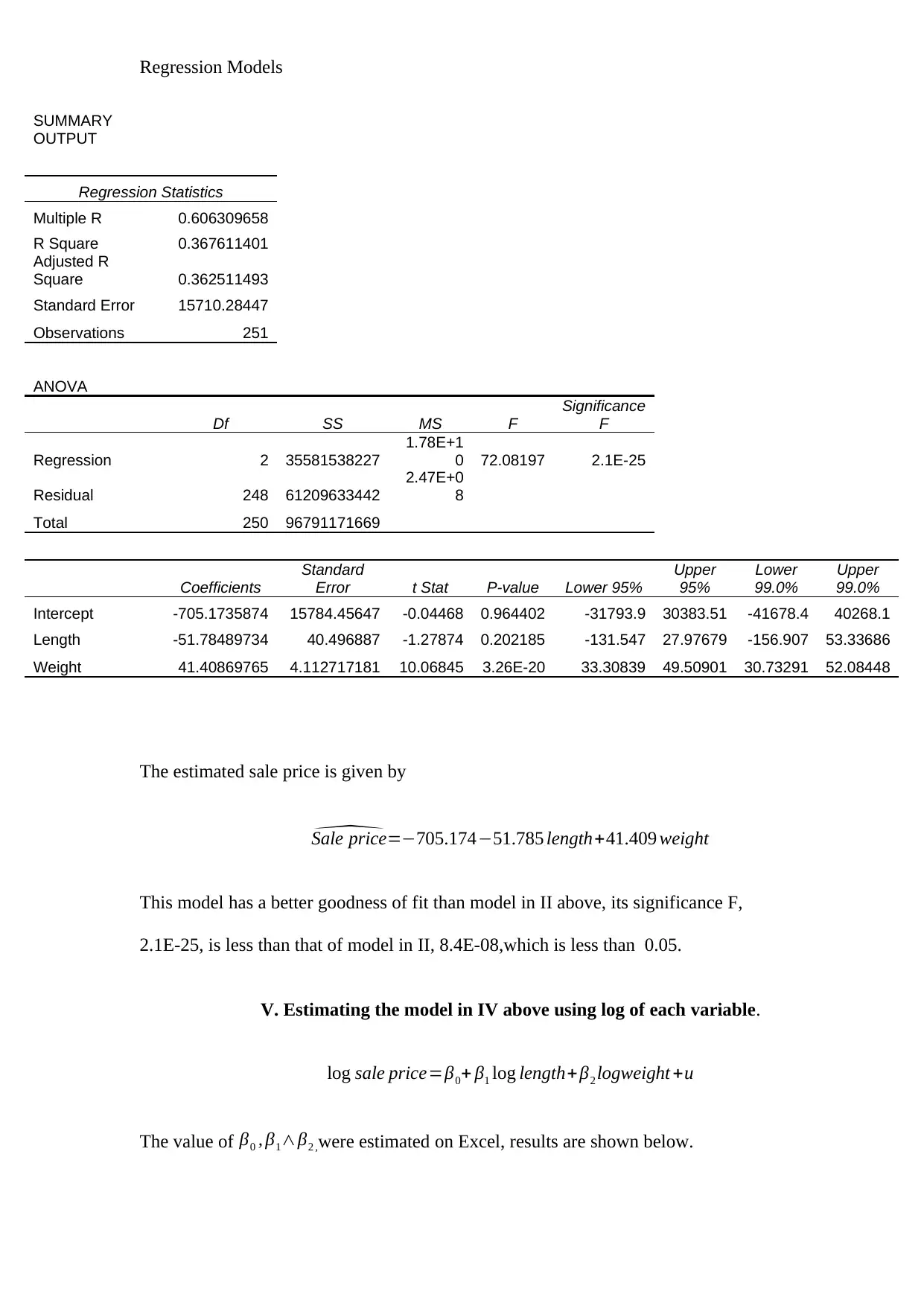
Multiple R 0.606309658
R Square 0.367611401
Adjusted R
Square 0.362511493
Standard Error 15710.28447
Observations 251
ANOVA
Df SS MS F
Significance
F
Regression 2 35581538227
1.78E+1
0 72.08197 2.1E-25
Residual 248 61209633442
2.47E+0
8
Total 250 96791171669
Coefficients
Standard
Error t Stat P-value Lower 95%
Upper
95%
Lower
99.0%
Upper
99.0%
Intercept -705.1735874 15784.45647 -0.04468 0.964402 -31793.9 30383.51 -41678.4 40268.1
Length -51.78489734 40.496887 -1.27874 0.202185 -131.547 27.97679 -156.907 53.33686
Weight 41.40869765 4.112717181 10.06845 3.26E-20 33.30839 49.50901 30.73291 52.08448
The estimated sale price is given by
^Sale price=−705.174−51.785 length+41.409 weight
This model has a better goodness of fit than model in II above, its significance F,
2.1E-25, is less than that of model in II, 8.4E-08,which is less than 0.05.
V. Estimating the model in IV above using log of each variable.
log sale price=β0+ β1 log length+β2 logweight +u
The value of β0 , β1∧β2 ,were estimated on Excel, results are shown below.
SUMMARY
OUTPUT
Regression Statistics
Multiple R 0.606309658
R Square 0.367611401
Adjusted R
Square 0.362511493
Standard Error 15710.28447
Observations 251
ANOVA
Df SS MS F
Significance
F
Regression 2 35581538227
1.78E+1
0 72.08197 2.1E-25
Residual 248 61209633442
2.47E+0
8
Total 250 96791171669
Coefficients
Standard
Error t Stat P-value Lower 95%
Upper
95%
Lower
99.0%
Upper
99.0%
Intercept -705.1735874 15784.45647 -0.04468 0.964402 -31793.9 30383.51 -41678.4 40268.1
Length -51.78489734 40.496887 -1.27874 0.202185 -131.547 27.97679 -156.907 53.33686
Weight 41.40869765 4.112717181 10.06845 3.26E-20 33.30839 49.50901 30.73291 52.08448
The estimated sale price is given by
^Sale price=−705.174−51.785 length+41.409 weight
This model has a better goodness of fit than model in II above, its significance F,
2.1E-25, is less than that of model in II, 8.4E-08,which is less than 0.05.
V. Estimating the model in IV above using log of each variable.
log sale price=β0+ β1 log length+β2 logweight +u
The value of β0 , β1∧β2 ,were estimated on Excel, results are shown below.
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

Regression Models
SUMMARY OUTPUT
Regression Statistics
Multiple R 0.725841
R Square 0.526846
Adjusted R
Square 0.52303
Standard
Error 0.134572
Observations 251
ANOVA
df SS MS F
Significance
F
Regression 2 5.00082 2.50041 138.071 5.02E-41
Residual 248 4.49118 0.01811
Total 250 9.491999
Coefficients
Standard
Error t Stat P-value Lower 95%
Upper
95%
Lower
99.0%
Upper
99.0%
Intercept 0.507216 0.804954 0.630118 0.529198 -1.0782 2.092633 -1.58228 2.596713
Log Length -0.61182 0.379339 -1.61285 0.10805 -1.35895 0.135322 -1.5965 0.372873
Log Weight 1.783179 0.131293 13.58171 8.74E-32 1.524588 2.04177 1.44237 2.123989
The estimated log sale price model is given by;
^log sale price ¿ 0.507−0.611 loglength+1.783 logweight
VI. Testing whether length has a negative effect on sale price at 1%
significance level.
Null hypothesis: Length has a negative effect on sale price.
From the above table, the P-value of Log length is 0.10805 which is greater than 0.05.
This suggests that the length is not statistically significant at 1% level, the null
hypothesis will be rejected (Aiken, West & Reno 1991). As a result, length does not
have negative effects on the sale price.
SUMMARY OUTPUT
Regression Statistics
Multiple R 0.725841
R Square 0.526846
Adjusted R
Square 0.52303
Standard
Error 0.134572
Observations 251
ANOVA
df SS MS F
Significance
F
Regression 2 5.00082 2.50041 138.071 5.02E-41
Residual 248 4.49118 0.01811
Total 250 9.491999
Coefficients
Standard
Error t Stat P-value Lower 95%
Upper
95%
Lower
99.0%
Upper
99.0%
Intercept 0.507216 0.804954 0.630118 0.529198 -1.0782 2.092633 -1.58228 2.596713
Log Length -0.61182 0.379339 -1.61285 0.10805 -1.35895 0.135322 -1.5965 0.372873
Log Weight 1.783179 0.131293 13.58171 8.74E-32 1.524588 2.04177 1.44237 2.123989
The estimated log sale price model is given by;
^log sale price ¿ 0.507−0.611 loglength+1.783 logweight
VI. Testing whether length has a negative effect on sale price at 1%
significance level.
Null hypothesis: Length has a negative effect on sale price.
From the above table, the P-value of Log length is 0.10805 which is greater than 0.05.
This suggests that the length is not statistically significant at 1% level, the null
hypothesis will be rejected (Aiken, West & Reno 1991). As a result, length does not
have negative effects on the sale price.
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
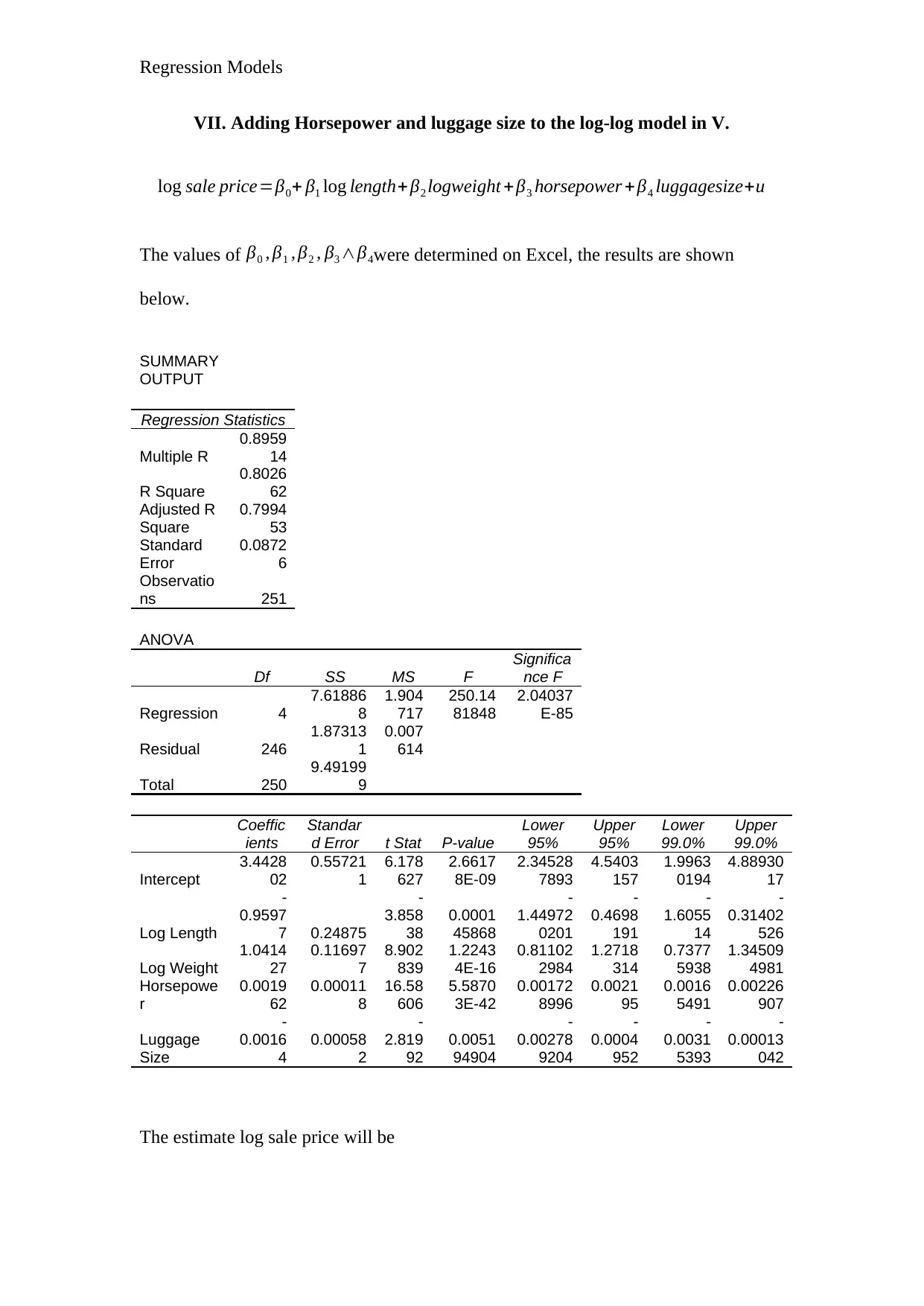
Regression Models
VII. Adding Horsepower and luggage size to the log-log model in V.
log sale price=β0+ β1 log length+β2 logweight +β3 horsepower + β4 luggagesize+u
The values of β0 , β1 , β2 , β3 ∧β4were determined on Excel, the results are shown
below.
SUMMARY
OUTPUT
Regression Statistics
Multiple R
0.8959
14
R Square
0.8026
62
Adjusted R
Square
0.7994
53
Standard
Error
0.0872
6
Observatio
ns 251
ANOVA
Df SS MS F
Significa
nce F
Regression 4
7.61886
8
1.904
717
250.14
81848
2.04037
E-85
Residual 246
1.87313
1
0.007
614
Total 250
9.49199
9
Coeffic
ients
Standar
d Error t Stat P-value
Lower
95%
Upper
95%
Lower
99.0%
Upper
99.0%
Intercept
3.4428
02
0.55721
1
6.178
627
2.6617
8E-09
2.34528
7893
4.5403
157
1.9963
0194
4.88930
17
Log Length
-
0.9597
7 0.24875
-
3.858
38
0.0001
45868
-
1.44972
0201
-
0.4698
191
-
1.6055
14
-
0.31402
526
Log Weight
1.0414
27
0.11697
7
8.902
839
1.2243
4E-16
0.81102
2984
1.2718
314
0.7377
5938
1.34509
4981
Horsepowe
r
0.0019
62
0.00011
8
16.58
606
5.5870
3E-42
0.00172
8996
0.0021
95
0.0016
5491
0.00226
907
Luggage
Size
-
0.0016
4
0.00058
2
-
2.819
92
0.0051
94904
-
0.00278
9204
-
0.0004
952
-
0.0031
5393
-
0.00013
042
The estimate log sale price will be
VII. Adding Horsepower and luggage size to the log-log model in V.
log sale price=β0+ β1 log length+β2 logweight +β3 horsepower + β4 luggagesize+u
The values of β0 , β1 , β2 , β3 ∧β4were determined on Excel, the results are shown
below.
SUMMARY
OUTPUT
Regression Statistics
Multiple R
0.8959
14
R Square
0.8026
62
Adjusted R
Square
0.7994
53
Standard
Error
0.0872
6
Observatio
ns 251
ANOVA
Df SS MS F
Significa
nce F
Regression 4
7.61886
8
1.904
717
250.14
81848
2.04037
E-85
Residual 246
1.87313
1
0.007
614
Total 250
9.49199
9
Coeffic
ients
Standar
d Error t Stat P-value
Lower
95%
Upper
95%
Lower
99.0%
Upper
99.0%
Intercept
3.4428
02
0.55721
1
6.178
627
2.6617
8E-09
2.34528
7893
4.5403
157
1.9963
0194
4.88930
17
Log Length
-
0.9597
7 0.24875
-
3.858
38
0.0001
45868
-
1.44972
0201
-
0.4698
191
-
1.6055
14
-
0.31402
526
Log Weight
1.0414
27
0.11697
7
8.902
839
1.2243
4E-16
0.81102
2984
1.2718
314
0.7377
5938
1.34509
4981
Horsepowe
r
0.0019
62
0.00011
8
16.58
606
5.5870
3E-42
0.00172
8996
0.0021
95
0.0016
5491
0.00226
907
Luggage
Size
-
0.0016
4
0.00058
2
-
2.819
92
0.0051
94904
-
0.00278
9204
-
0.0004
952
-
0.0031
5393
-
0.00013
042
The estimate log sale price will be

Regression Models
^log sale price ¿ 3.443−0.9596 loglength+1.041 logweight
From the information in the table above, Horsepower is statistically significant at 1%
level, since its P-value, 5.58703E-42 is less than 0.05. Similarly, Luggage size is
significant because its P-value, 0.005194904 is also less than 0.05. The two variables
are jointly significant at 5%, as 0, which is null the hypothesis is not within their 95%
confidence interval brackets are above.
VIII. The overall significance of the model in VII above at 1%.
The overall significance is determined using the significance F. The significance
F, 2.04037E-85, is less than 0.05. This indicates that one of the variables is
statistically significant. This means the model is good for the estimation of the
sale price.
IX. Testing whether Luxury cars are more expensive than other types of cars
Null hypothesis: Luxury car are not more expensive than other types of cars
^log sale price ¿ 3.443−0.9596 loglength+1.041 logweight
From the information in the table above, Horsepower is statistically significant at 1%
level, since its P-value, 5.58703E-42 is less than 0.05. Similarly, Luggage size is
significant because its P-value, 0.005194904 is also less than 0.05. The two variables
are jointly significant at 5%, as 0, which is null the hypothesis is not within their 95%
confidence interval brackets are above.
VIII. The overall significance of the model in VII above at 1%.
The overall significance is determined using the significance F. The significance
F, 2.04037E-85, is less than 0.05. This indicates that one of the variables is
statistically significant. This means the model is good for the estimation of the
sale price.
IX. Testing whether Luxury cars are more expensive than other types of cars
Null hypothesis: Luxury car are not more expensive than other types of cars
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
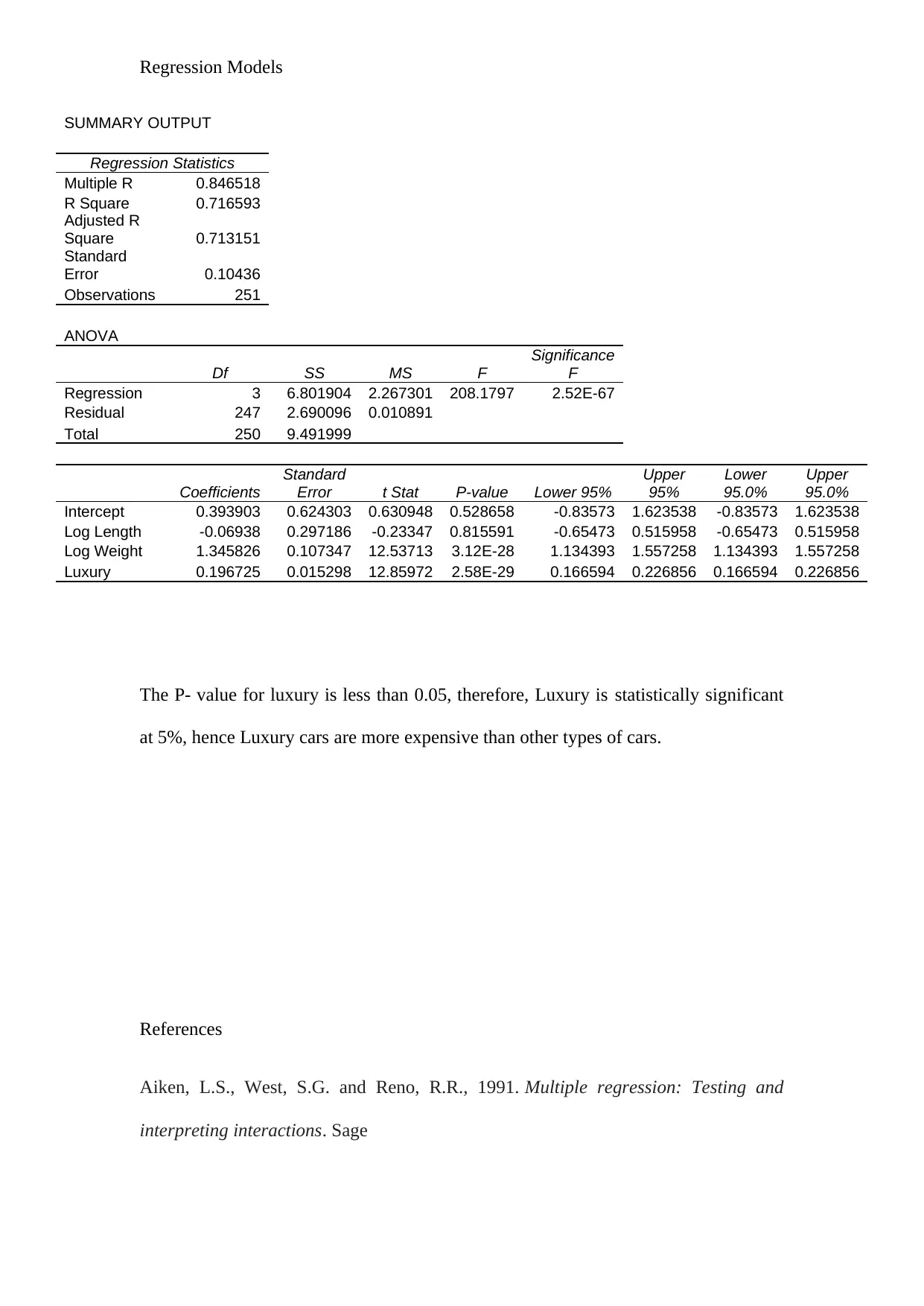
Regression Models
SUMMARY OUTPUT
Regression Statistics
Multiple R 0.846518
R Square 0.716593
Adjusted R
Square 0.713151
Standard
Error 0.10436
Observations 251
ANOVA
Df SS MS F
Significance
F
Regression 3 6.801904 2.267301 208.1797 2.52E-67
Residual 247 2.690096 0.010891
Total 250 9.491999
Coefficients
Standard
Error t Stat P-value Lower 95%
Upper
95%
Lower
95.0%
Upper
95.0%
Intercept 0.393903 0.624303 0.630948 0.528658 -0.83573 1.623538 -0.83573 1.623538
Log Length -0.06938 0.297186 -0.23347 0.815591 -0.65473 0.515958 -0.65473 0.515958
Log Weight 1.345826 0.107347 12.53713 3.12E-28 1.134393 1.557258 1.134393 1.557258
Luxury 0.196725 0.015298 12.85972 2.58E-29 0.166594 0.226856 0.166594 0.226856
The P- value for luxury is less than 0.05, therefore, Luxury is statistically significant
at 5%, hence Luxury cars are more expensive than other types of cars.
References
Aiken, L.S., West, S.G. and Reno, R.R., 1991. Multiple regression: Testing and
interpreting interactions. Sage
SUMMARY OUTPUT
Regression Statistics
Multiple R 0.846518
R Square 0.716593
Adjusted R
Square 0.713151
Standard
Error 0.10436
Observations 251
ANOVA
Df SS MS F
Significance
F
Regression 3 6.801904 2.267301 208.1797 2.52E-67
Residual 247 2.690096 0.010891
Total 250 9.491999
Coefficients
Standard
Error t Stat P-value Lower 95%
Upper
95%
Lower
95.0%
Upper
95.0%
Intercept 0.393903 0.624303 0.630948 0.528658 -0.83573 1.623538 -0.83573 1.623538
Log Length -0.06938 0.297186 -0.23347 0.815591 -0.65473 0.515958 -0.65473 0.515958
Log Weight 1.345826 0.107347 12.53713 3.12E-28 1.134393 1.557258 1.134393 1.557258
Luxury 0.196725 0.015298 12.85972 2.58E-29 0.166594 0.226856 0.166594 0.226856
The P- value for luxury is less than 0.05, therefore, Luxury is statistically significant
at 5%, hence Luxury cars are more expensive than other types of cars.
References
Aiken, L.S., West, S.G. and Reno, R.R., 1991. Multiple regression: Testing and
interpreting interactions. Sage
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

Regression Models
Bernstein, S. and Bernstein, R., 1998. Schaum's Outline of Elements of Statistics I:
Descriptive Statistics and Probability. McGraw-Hill Companies.
Brase, C.H. and Brase, C.P., 2011. Understandable statistics: Concepts and methods.
Cengage Learning.
Data, S. and Using Descriptive Statistics Bartz, A.E., 1988. Basic statistical concepts.
New York: Macmillan. Devore, J., and Peck.
Francis, A., 2004. Business mathematics and statistics. Cengage Learning EMEA.
Goos, P. and Meintrup, D., 2015. Statistics with JMP: graphs, descriptive statistics
and probability. John Wiley & Sons.
Hassett, M.J. and Stewart, D., 2006. Probability for risk management. Actex
Publications
Sharma, J.K., 2007. Business statistics. Pearson Education India.
.
.
Bernstein, S. and Bernstein, R., 1998. Schaum's Outline of Elements of Statistics I:
Descriptive Statistics and Probability. McGraw-Hill Companies.
Brase, C.H. and Brase, C.P., 2011. Understandable statistics: Concepts and methods.
Cengage Learning.
Data, S. and Using Descriptive Statistics Bartz, A.E., 1988. Basic statistical concepts.
New York: Macmillan. Devore, J., and Peck.
Francis, A., 2004. Business mathematics and statistics. Cengage Learning EMEA.
Goos, P. and Meintrup, D., 2015. Statistics with JMP: graphs, descriptive statistics
and probability. John Wiley & Sons.
Hassett, M.J. and Stewart, D., 2006. Probability for risk management. Actex
Publications
Sharma, J.K., 2007. Business statistics. Pearson Education India.
.
.
1 out of 11
Related Documents
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
Copyright © 2020–2025 A2Z Services. All Rights Reserved. Developed and managed by ZUCOL.




