Design of Double Reduction Spur Gearbox - Desklib
VerifiedAdded on 2022/10/19
|20
|1276
|309
AI Summary
This report discusses the design of a double reduction spur gearbox, including material selection, gear drive design requirements, and the importance of gear oil. The report provides a solution for the design of the gearbox, including the selection of bearings. The report also includes references for further reading.
Contribute Materials
Your contribution can guide someone’s learning journey. Share your
documents today.

REPORT
ON
DESIGN
OF
DOUBLE REDUCTION SPUR GEARBOX
ON
DESIGN
OF
DOUBLE REDUCTION SPUR GEARBOX
Secure Best Marks with AI Grader
Need help grading? Try our AI Grader for instant feedback on your assignments.

Nomenclature
N1= Speed of pinion 1 in RPM
N2= Speed of Gear 1 in RPM
N3= Speed of pinion 2 in RPM
N4= Speed of Gear 2 in RPM
Z1= Number of teeth on pinion 1
Z2= Number of teeth on Gear 1
D1= Pitch circle diameter of pinion 1
D2= Pitch circle diameter of gear 1
D3= Pitch circle diameter of pinion 2
D4= Pitch circle diameter of gear 2
Y = Lewis factor
m = Module
b = Face width
CD =Centre distance between gears
σ c1= Contact stress
Fs =Pinion/gear strength
Fd =Dynamic load
FT =Transmission load
ds 1 =Input shaft diameter
ds 2 =Intermediate shaft diameter
ds 3 =Output shaft diameter
V =Velocity of gear/pinion
N1= Speed of pinion 1 in RPM
N2= Speed of Gear 1 in RPM
N3= Speed of pinion 2 in RPM
N4= Speed of Gear 2 in RPM
Z1= Number of teeth on pinion 1
Z2= Number of teeth on Gear 1
D1= Pitch circle diameter of pinion 1
D2= Pitch circle diameter of gear 1
D3= Pitch circle diameter of pinion 2
D4= Pitch circle diameter of gear 2
Y = Lewis factor
m = Module
b = Face width
CD =Centre distance between gears
σ c1= Contact stress
Fs =Pinion/gear strength
Fd =Dynamic load
FT =Transmission load
ds 1 =Input shaft diameter
ds 2 =Intermediate shaft diameter
ds 3 =Output shaft diameter
V =Velocity of gear/pinion

REDUCTION TYPE GEARBOX
Gearbox is a mechanical device generally used to transmit power from source to output
shaft. Power can be transmit by set of gears aligned in such a manner to get desired output
in required direction. Reduction type gearbox is used where input speed can be reduced to
get low speed at high torque ,The number of gears used in this system is completely depend
on reduction ratio and input speed .
Material Selection
For selecting material of gears, the following data need be calculated:
Speed of driving and driven gear
Gear ratio
Power transmitted
Centre distance between meshed gears.
Gear drive design requirements
The main requirements to design a gear drive shown below:
Gear teeth should have fatigue and wear characteristics to work satisfactory in its
designed life.
It is required that gear teeth have sufficient strength that it can withstand static and
dynamic loading so that it may not fail under during working conditions.
Proper utilization of space.
Deflection of shaft and gear alignment need to be considered as it highly effect the
performance.
Material used to be economical and easily available.
For efficient performance, the lubrication in gears is necessary.
Based on requirements, materials available for gear shown below.
Fig 1 : Material list for gears
Gearbox is a mechanical device generally used to transmit power from source to output
shaft. Power can be transmit by set of gears aligned in such a manner to get desired output
in required direction. Reduction type gearbox is used where input speed can be reduced to
get low speed at high torque ,The number of gears used in this system is completely depend
on reduction ratio and input speed .
Material Selection
For selecting material of gears, the following data need be calculated:
Speed of driving and driven gear
Gear ratio
Power transmitted
Centre distance between meshed gears.
Gear drive design requirements
The main requirements to design a gear drive shown below:
Gear teeth should have fatigue and wear characteristics to work satisfactory in its
designed life.
It is required that gear teeth have sufficient strength that it can withstand static and
dynamic loading so that it may not fail under during working conditions.
Proper utilization of space.
Deflection of shaft and gear alignment need to be considered as it highly effect the
performance.
Material used to be economical and easily available.
For efficient performance, the lubrication in gears is necessary.
Based on requirements, materials available for gear shown below.
Fig 1 : Material list for gears

Material for Shafts
Essential property of shaft material :-
High strength
High wear resistant
Low notch sensitivity factor
Good machinability
Fig 2 : Material list for shaft
Material for Casing
Essential property of casing material:–
High strength
Less weight
High ductility
Fig 3 : Material list for casing
IMPORTANCE OF GEAR OIL (LUBRICATION)
Gear oil is one of the most important part of gearbox due to its following benefits:-
Gear oil provides lubrication to the different parts of gearbox.
Reduce friction between mating parts cause less wear and tear.
Increase life of gears.
Act as a cooling agent and maintain temperature in casing chamber.
Remove dirt and wear off parts from gearbox parts.
Essential property of shaft material :-
High strength
High wear resistant
Low notch sensitivity factor
Good machinability
Fig 2 : Material list for shaft
Material for Casing
Essential property of casing material:–
High strength
Less weight
High ductility
Fig 3 : Material list for casing
IMPORTANCE OF GEAR OIL (LUBRICATION)
Gear oil is one of the most important part of gearbox due to its following benefits:-
Gear oil provides lubrication to the different parts of gearbox.
Reduce friction between mating parts cause less wear and tear.
Increase life of gears.
Act as a cooling agent and maintain temperature in casing chamber.
Remove dirt and wear off parts from gearbox parts.
Secure Best Marks with AI Grader
Need help grading? Try our AI Grader for instant feedback on your assignments.
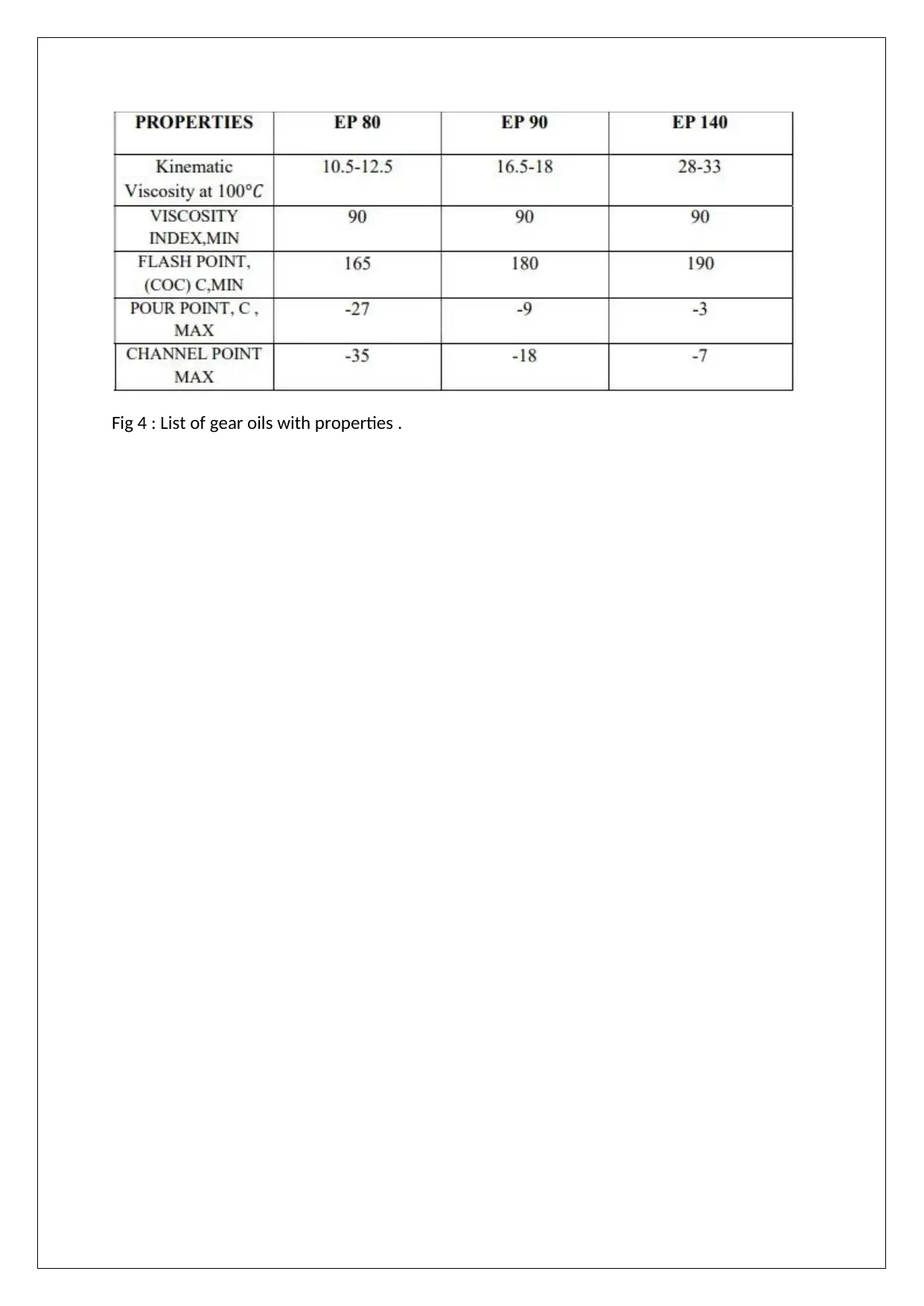
Fig 4 : List of gear oils with properties .

Design requirements
Mass of castings: 450Kg
Lift height: 8m
As an assumption the radius of drum: 250mm (can be changed in the design)
Torque to be delivered on the assumed drum radius of 250mm: 112N.m
Power to be delivered: 15kW (this is maximum and can be changed)
Input speed: 30rev/s
Output speed: 2rev/s
Loads have a moderate shock effect on the winch
Output shaft and input shafts in-line or at right angles
Base mounted with 4 bolts
Continuous operation
6-year life, 8 hours a day, 5 days a week
Low maintenance
Competitive cost
Nominal operating conditions of industrial locations
Input and output shafts are standard size for typical couplings.
Include safety factor of 2
Low noise <85dB
GIVEN DATA
Input power =15 kW
Torque T =112 Nm
Input speed = 30 rev / sec
Output required speed = 2 rev /sec
SOLUTION (ROBERT,2013)
Mass of castings: 450Kg
Lift height: 8m
As an assumption the radius of drum: 250mm (can be changed in the design)
Torque to be delivered on the assumed drum radius of 250mm: 112N.m
Power to be delivered: 15kW (this is maximum and can be changed)
Input speed: 30rev/s
Output speed: 2rev/s
Loads have a moderate shock effect on the winch
Output shaft and input shafts in-line or at right angles
Base mounted with 4 bolts
Continuous operation
6-year life, 8 hours a day, 5 days a week
Low maintenance
Competitive cost
Nominal operating conditions of industrial locations
Input and output shafts are standard size for typical couplings.
Include safety factor of 2
Low noise <85dB
GIVEN DATA
Input power =15 kW
Torque T =112 Nm
Input speed = 30 rev / sec
Output required speed = 2 rev /sec
SOLUTION (ROBERT,2013)

Input speed in rpm
ω1= 2 π N 1
60
30=2 π N1
60
N1 ≈ 300rpm
Output speed in rpm
ω4= 2 π N 4
60
2= 2 π N 4
60
N4 =20 rpm
Total reduction in gearbox required
Speed ratio = ω1
ω4
Speed ratio = 30
2 =15
Now from above calculation, it is clear that 15 times reduced speed is required at the output
gear i.e. gear 4. As double reduction spur gearbox is needed to be design to deliver 15 times
less speed .The reduction should be done in two stages.
First stage reduction = 4:1
Second stage reduction = 3.75:1
DESIGN FOR FIRST STAGE REDUCTION
Gear ratio required = 4:1
Speed at input shaft /Input pinion N1=300 rpm
Pressure angle α =20 °
Minimum number of teeth to avoid interference Z1 = 2
sin2 α
Z1 = 2
sin2 20
ω1= 2 π N 1
60
30=2 π N1
60
N1 ≈ 300rpm
Output speed in rpm
ω4= 2 π N 4
60
2= 2 π N 4
60
N4 =20 rpm
Total reduction in gearbox required
Speed ratio = ω1
ω4
Speed ratio = 30
2 =15
Now from above calculation, it is clear that 15 times reduced speed is required at the output
gear i.e. gear 4. As double reduction spur gearbox is needed to be design to deliver 15 times
less speed .The reduction should be done in two stages.
First stage reduction = 4:1
Second stage reduction = 3.75:1
DESIGN FOR FIRST STAGE REDUCTION
Gear ratio required = 4:1
Speed at input shaft /Input pinion N1=300 rpm
Pressure angle α =20 °
Minimum number of teeth to avoid interference Z1 = 2
sin2 α
Z1 = 2
sin2 20
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

Z1 =18
Therefore number of teeth on pinion 1 is 18
Speed of Gear 1
N1
N 2
=4 :1
300
N2
=4 :1
N2=75 rpm
Number of teeth on Gear 1
Z2
Z1
=4 :1
Z2
18 =4 :1
Z2 =72
Calculate lewis factor (Y)
Y =π∗y
y=0.154− 0.912
Z
For pinion 1
Y 1=π∗y1
y1=0.154− 0.912
Z1
Y 1= (0.154− 0.912
18 )∗π
Y 1=0.325
For gear
Y 2=π∗y2
Therefore number of teeth on pinion 1 is 18
Speed of Gear 1
N1
N 2
=4 :1
300
N2
=4 :1
N2=75 rpm
Number of teeth on Gear 1
Z2
Z1
=4 :1
Z2
18 =4 :1
Z2 =72
Calculate lewis factor (Y)
Y =π∗y
y=0.154− 0.912
Z
For pinion 1
Y 1=π∗y1
y1=0.154− 0.912
Z1
Y 1= (0.154− 0.912
18 )∗π
Y 1=0.325
For gear
Y 2=π∗y2

y2=0.154− 0.912
Z2
Y 2= (0.154− 0.912
72 )∗π
Y 2=0.443
Material selected for gear and pinion
S.No Item Material σ c σ b
1 Gear 15Ni2Cr1Mo15 950 MPa 320 MPa
2 Pinion 40Ni2Cr1Mo28 1300 MPa 500 MPa
Now determine weaker part from gear and pinion.
For pinion 1
S1=σb 1∗Y 1
S1=500∗0.325
S1=162.5
For Gear 1
S2=σb 2∗Y 2
S2=320∗0.443
S2=141.76
From above calculation, S1 > S2 , Therefore pinion is weaker section , so design need to be
done for pinion .
Module (m)
m=1.26∗3
√ T
Y 1∗σb 1∗∅ m∗Z1
∅ m=10 (for gears)
Z2
Y 2= (0.154− 0.912
72 )∗π
Y 2=0.443
Material selected for gear and pinion
S.No Item Material σ c σ b
1 Gear 15Ni2Cr1Mo15 950 MPa 320 MPa
2 Pinion 40Ni2Cr1Mo28 1300 MPa 500 MPa
Now determine weaker part from gear and pinion.
For pinion 1
S1=σb 1∗Y 1
S1=500∗0.325
S1=162.5
For Gear 1
S2=σb 2∗Y 2
S2=320∗0.443
S2=141.76
From above calculation, S1 > S2 , Therefore pinion is weaker section , so design need to be
done for pinion .
Module (m)
m=1.26∗3
√ T
Y 1∗σb 1∗∅ m∗Z1
∅ m=10 (for gears)

m=1.26∗3
√ 112∗1000
0.325∗500∗10∗18
m=2
Now check for contact stress
Centre distance between gear and pinion (CD)
CD= m(Z1 + Z2 )
2
CD= 2(18+72)
2
CD=90 mm
Face width (b)
b=9∗m
b=9∗2
b=18 mm
Contact stress
σ c1=0.74∗( G . R+1
CD ) √ G. R+1
2∗G . R∗b ∗E∗T
Gear ratio G . R=4 :1
Young modulus E=210 GPa
σ c1=0.74∗( 4 +1
90 ) √ 4+1
2∗4∗18∗210∗1000∗112∗1000
σ c1=1174 MPa
As contact stress greater than σ c1 i.e. 1300 > 1174, therefore pinion won’t fail in stress.
Now check for dynamic load
For safe loading Fs > Fd
Where, Fs= strength of pinion
Fd = strength of dynamic load
√ 112∗1000
0.325∗500∗10∗18
m=2
Now check for contact stress
Centre distance between gear and pinion (CD)
CD= m(Z1 + Z2 )
2
CD= 2(18+72)
2
CD=90 mm
Face width (b)
b=9∗m
b=9∗2
b=18 mm
Contact stress
σ c1=0.74∗( G . R+1
CD ) √ G. R+1
2∗G . R∗b ∗E∗T
Gear ratio G . R=4 :1
Young modulus E=210 GPa
σ c1=0.74∗( 4 +1
90 ) √ 4+1
2∗4∗18∗210∗1000∗112∗1000
σ c1=1174 MPa
As contact stress greater than σ c1 i.e. 1300 > 1174, therefore pinion won’t fail in stress.
Now check for dynamic load
For safe loading Fs > Fd
Where, Fs= strength of pinion
Fd = strength of dynamic load
Secure Best Marks with AI Grader
Need help grading? Try our AI Grader for instant feedback on your assignments.

Calculate strength of pinion Fs
Fs=σb 1∗b∗m∗Y 1
Fs=500∗18∗2∗0.325
Fs=5850 N
Pitch circle diameter of pinion D1
D1=m∗Z1
D1=2∗18
D1=36 mm
Velocity of pinion V 1
V 1= π D1 N1
60
V 1= π∗36∗287
60∗1000
V 1=0.54 m/sec
Transmitted load Ft
Ft= 2∗T
D¿
Ft= 2∗112∗1000
250
Ft=896 N
Dynamic load Fd
Fd=Ft∗CV
CV = 5.5+ √V 1
5.5
CV = 5.5+ √0.54
5.5
CV =1.13
Fs=σb 1∗b∗m∗Y 1
Fs=500∗18∗2∗0.325
Fs=5850 N
Pitch circle diameter of pinion D1
D1=m∗Z1
D1=2∗18
D1=36 mm
Velocity of pinion V 1
V 1= π D1 N1
60
V 1= π∗36∗287
60∗1000
V 1=0.54 m/sec
Transmitted load Ft
Ft= 2∗T
D¿
Ft= 2∗112∗1000
250
Ft=896 N
Dynamic load Fd
Fd=Ft∗CV
CV = 5.5+ √V 1
5.5
CV = 5.5+ √0.54
5.5
CV =1.13

Fd=Ft∗CV
Fd=896∗1.13
Fd=1013 N
Since, Fs > Fd therefore strength of pinion is much greater than dynamic load, therefore pinion
won’t fail due to dynamic loading.
SHAFT DESIGN FOR PINION 1
T = π
16∗ds 1
3∗τ
ds 1 =Pinion shaft diameter
112∗1000= π
16 ∗ds 1
3∗130
ds 1 =16 mm
SHAFT DESIGN FOR GEAR 1
ds 2
ds 1
=3
√ G. R
ds 2 =Gear shaft diameter
ds 2
16 =3
√ 4
ds 2 =26 mm
Fd=896∗1.13
Fd=1013 N
Since, Fs > Fd therefore strength of pinion is much greater than dynamic load, therefore pinion
won’t fail due to dynamic loading.
SHAFT DESIGN FOR PINION 1
T = π
16∗ds 1
3∗τ
ds 1 =Pinion shaft diameter
112∗1000= π
16 ∗ds 1
3∗130
ds 1 =16 mm
SHAFT DESIGN FOR GEAR 1
ds 2
ds 1
=3
√ G. R
ds 2 =Gear shaft diameter
ds 2
16 =3
√ 4
ds 2 =26 mm

DESIGN FOR SECOND STAGE REDUCTION
Gear ratio required = 3.75:1
Speed at intermediate shaft/ pinion2 N2=75 rpm
Pressure angle α =20 °
Z3 =22
Speed of pinion 2
N3
N 4
=3.75 :1
N 3
20 =3.75:1
N3=75 rpm
As gear 1 and pinion2 are mounted on the same shaft therefore their speeds are same .
Number of teeth on Gear 2
Z4
Z3
=3.75 :1
Z4
22 =3.75:1
Z4=84
Calculate lewis factor (Y)
Y =π∗y
y=0.154− 0.912
Z
For pinion 2
Y 3=π∗y3
y3=0.154− 0.912
Z3
Y 3= (0.154− 0.912
22 )∗π
Y 3=0.353
Gear ratio required = 3.75:1
Speed at intermediate shaft/ pinion2 N2=75 rpm
Pressure angle α =20 °
Z3 =22
Speed of pinion 2
N3
N 4
=3.75 :1
N 3
20 =3.75:1
N3=75 rpm
As gear 1 and pinion2 are mounted on the same shaft therefore their speeds are same .
Number of teeth on Gear 2
Z4
Z3
=3.75 :1
Z4
22 =3.75:1
Z4=84
Calculate lewis factor (Y)
Y =π∗y
y=0.154− 0.912
Z
For pinion 2
Y 3=π∗y3
y3=0.154− 0.912
Z3
Y 3= (0.154− 0.912
22 )∗π
Y 3=0.353
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
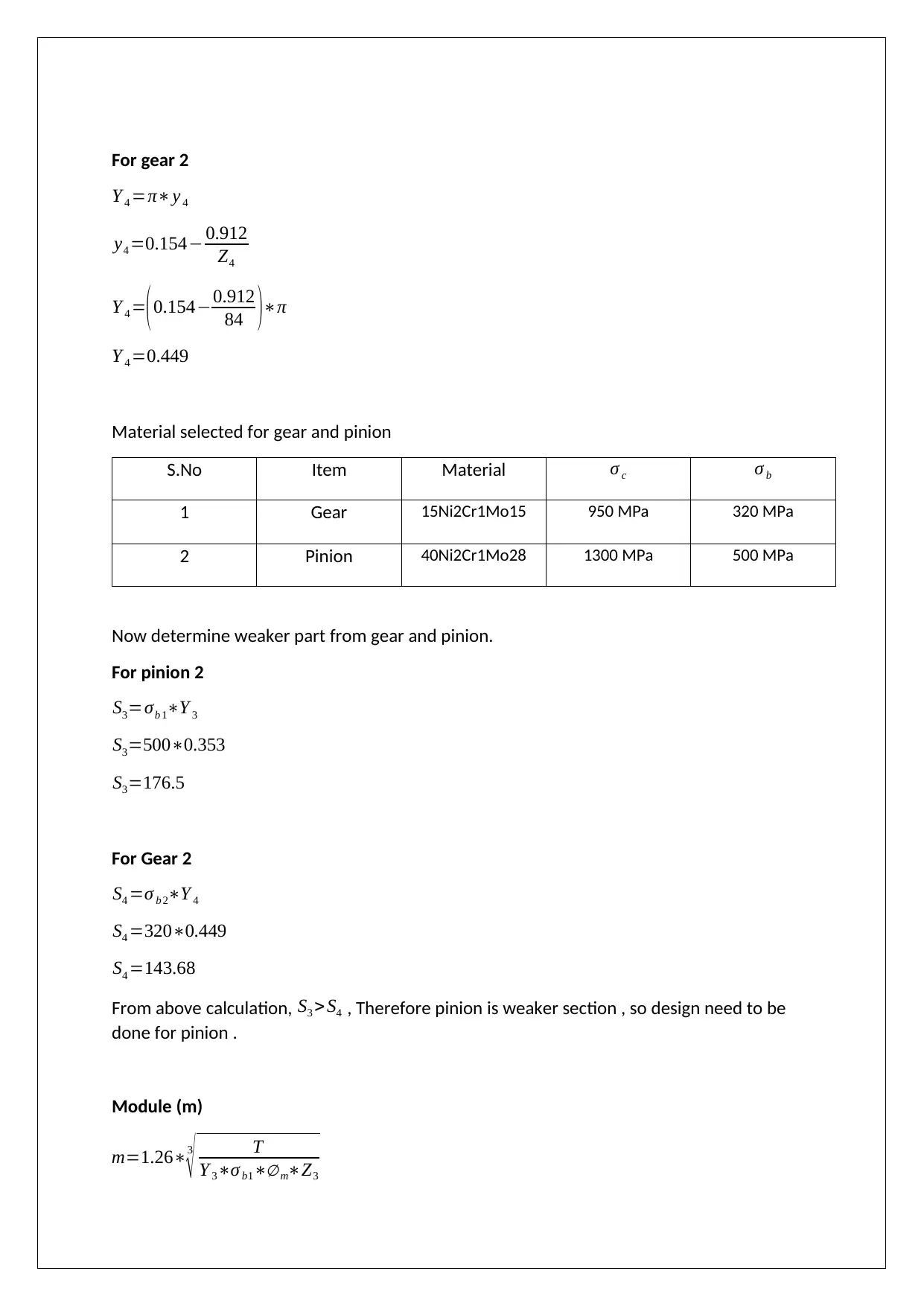
For gear 2
Y 4 =π∗y 4
y4 =0.154− 0.912
Z4
Y 4 =( 0.154−0.912
84 )∗π
Y 4 =0.449
Material selected for gear and pinion
S.No Item Material σ c σ b
1 Gear 15Ni2Cr1Mo15 950 MPa 320 MPa
2 Pinion 40Ni2Cr1Mo28 1300 MPa 500 MPa
Now determine weaker part from gear and pinion.
For pinion 2
S3=σb 1∗Y 3
S3=500∗0.353
S3=176.5
For Gear 2
S4 =σ b 2∗Y 4
S4 =320∗0.449
S4 =143.68
From above calculation, S3 > S4 , Therefore pinion is weaker section , so design need to be
done for pinion .
Module (m)
m=1.26∗3
√ T
Y 3∗σ b1∗∅ m∗Z3
Y 4 =π∗y 4
y4 =0.154− 0.912
Z4
Y 4 =( 0.154−0.912
84 )∗π
Y 4 =0.449
Material selected for gear and pinion
S.No Item Material σ c σ b
1 Gear 15Ni2Cr1Mo15 950 MPa 320 MPa
2 Pinion 40Ni2Cr1Mo28 1300 MPa 500 MPa
Now determine weaker part from gear and pinion.
For pinion 2
S3=σb 1∗Y 3
S3=500∗0.353
S3=176.5
For Gear 2
S4 =σ b 2∗Y 4
S4 =320∗0.449
S4 =143.68
From above calculation, S3 > S4 , Therefore pinion is weaker section , so design need to be
done for pinion .
Module (m)
m=1.26∗3
√ T
Y 3∗σ b1∗∅ m∗Z3

∅ m=10 (for gears)
m=1.26∗3
√ 112∗1000
0.353∗500∗10∗22
m=2
Now check for contact stress
Centre distance between gear and pinion (CD)
CD= m(Z1 + Z2 )
2
CD= 2(22+84)
2
CD=106 mm
Face width (b)
b=9∗m
b=9∗2
b=18 mm
Contact stress
σ c1=0.74∗( G . R+1
CD ) √ G. R+1
2∗G . R∗b ∗E∗T
Gear ratio G . R=3.75 :1
Young modulus E=210 GPa
σ c1=0.74∗( 3.75+1
106 ) √ 3.75+1
2∗3.75∗22∗210∗1000∗112∗1000
σ c1=863 MPa
As contact stress greater than σ c1 i.e. 1300 > 863, therefore pinion won’t fail in stress.
Now check for dynamic load
For safe loading Fs > Fd
Where, Fs= strength of pinion
Fd = strength of dynamic load
m=1.26∗3
√ 112∗1000
0.353∗500∗10∗22
m=2
Now check for contact stress
Centre distance between gear and pinion (CD)
CD= m(Z1 + Z2 )
2
CD= 2(22+84)
2
CD=106 mm
Face width (b)
b=9∗m
b=9∗2
b=18 mm
Contact stress
σ c1=0.74∗( G . R+1
CD ) √ G. R+1
2∗G . R∗b ∗E∗T
Gear ratio G . R=3.75 :1
Young modulus E=210 GPa
σ c1=0.74∗( 3.75+1
106 ) √ 3.75+1
2∗3.75∗22∗210∗1000∗112∗1000
σ c1=863 MPa
As contact stress greater than σ c1 i.e. 1300 > 863, therefore pinion won’t fail in stress.
Now check for dynamic load
For safe loading Fs > Fd
Where, Fs= strength of pinion
Fd = strength of dynamic load

Calculate strength of pinion Fs
Fs=σb 1∗b∗m∗Y 3
Fs=500∗22∗2∗0.353
Fs=7767 N
Pitch circle diameter of pinion D3
D3=m∗Z3
D1=2∗22
D1=44 mm
Velocity of pinion V 3
V 3= π D3 N3
60
V 1= π∗44∗75
60∗1000
V 1=0.2 m/sec
Transmitted load Ft
Ft= 2∗T
D¿
Ft= 2∗112∗1000
250
Ft=896 N
Dynamic load Fd
Fd=Ft∗CV
CV = 5.5+ √V 3
5.5
CV = 5.5+ √0.1
5.5
CV =1.05
Fs=σb 1∗b∗m∗Y 3
Fs=500∗22∗2∗0.353
Fs=7767 N
Pitch circle diameter of pinion D3
D3=m∗Z3
D1=2∗22
D1=44 mm
Velocity of pinion V 3
V 3= π D3 N3
60
V 1= π∗44∗75
60∗1000
V 1=0.2 m/sec
Transmitted load Ft
Ft= 2∗T
D¿
Ft= 2∗112∗1000
250
Ft=896 N
Dynamic load Fd
Fd=Ft∗CV
CV = 5.5+ √V 3
5.5
CV = 5.5+ √0.1
5.5
CV =1.05
Secure Best Marks with AI Grader
Need help grading? Try our AI Grader for instant feedback on your assignments.

Fd=Ft∗CV
Fd=896∗1.05
Fd=941 N
Since, Fs > Fd therefore strength of pinion is much greater than dynamic load, therefore pinion
won’t fail due to dynamic loading.
SHAFT DESIGN FOR PINION 2
T = π
16∗ds 2
3∗τ
ds 2 =Pinion shaft diameter
112∗1000= π
16 ∗ds 1
3∗130
ds 2 =16 mm
SHAFT DESIGN FOR GEAR 1
ds 3
ds 2
=3
√G. R
ds 3 =Gear shaft diameter
ds 3
16 =3
√3.5
ds 2 =26 mm
Fd=896∗1.05
Fd=941 N
Since, Fs > Fd therefore strength of pinion is much greater than dynamic load, therefore pinion
won’t fail due to dynamic loading.
SHAFT DESIGN FOR PINION 2
T = π
16∗ds 2
3∗τ
ds 2 =Pinion shaft diameter
112∗1000= π
16 ∗ds 1
3∗130
ds 2 =16 mm
SHAFT DESIGN FOR GEAR 1
ds 3
ds 2
=3
√G. R
ds 3 =Gear shaft diameter
ds 3
16 =3
√3.5
ds 2 =26 mm

SELECTIONS OF BEARINGS
Bearing is selected as per the dimensions and load requirements of shaft .
For input shaft , details of selected bearing is shown below :-
https://www.skf.com/in/products/bearings-units-housings/ball-bearings/deep-groove-ball-
bearings/deep-groove-ball-bearings/index.html?designation=62302-2RS1&unit=metricUnit
For intermediate shaft and output shaft , details of selected bearing is shown below :-
Bearing is selected as per the dimensions and load requirements of shaft .
For input shaft , details of selected bearing is shown below :-
https://www.skf.com/in/products/bearings-units-housings/ball-bearings/deep-groove-ball-
bearings/deep-groove-ball-bearings/index.html?designation=62302-2RS1&unit=metricUnit
For intermediate shaft and output shaft , details of selected bearing is shown below :-

https://www.skf.com/in/products/bearings-units-housings/ball-bearings/deep-groove-ball-
bearings/deep-groove-ball-bearings/index.html?designation=4205%20ATN9&unit=metricUnit
bearings/deep-groove-ball-bearings/index.html?designation=4205%20ATN9&unit=metricUnit
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

REFERENCES
ROBERT C. JUVINALL, KURT M. MARSHEK. Fundamentals of Machine Component Design, Fifth edition
Pg 657-663. Wiley Pub., 2013 .
Bearing cad model
https://www.skf.com/in/products/bearings-units-housings/ball-bearings/deep-groove-ball-
bearings/deep-groove-ball-bearings/index.html?designation=4205%20ATN9&unit=metricUnit
https://www.skf.com/in/products/bearings-units-housings/ball-bearings/deep-groove-ball-
bearings/deep-groove-ball-bearings/index.html?designation=62302-2RS1&unit=metricUnit
ROBERT C. JUVINALL, KURT M. MARSHEK. Fundamentals of Machine Component Design, Fifth edition
Pg 657-663. Wiley Pub., 2013 .
Bearing cad model
https://www.skf.com/in/products/bearings-units-housings/ball-bearings/deep-groove-ball-
bearings/deep-groove-ball-bearings/index.html?designation=4205%20ATN9&unit=metricUnit
https://www.skf.com/in/products/bearings-units-housings/ball-bearings/deep-groove-ball-
bearings/deep-groove-ball-bearings/index.html?designation=62302-2RS1&unit=metricUnit
1 out of 20
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
© 2024 | Zucol Services PVT LTD | All rights reserved.



