6112ICT/7113ICT Image Processing Methods Analysis and Testing Report
VerifiedAdded on 2023/01/10
|8
|4305
|99
Report
AI Summary
This report presents an empirical approach for evaluating the performance of image processing programs. The study focuses on direct testing methods, utilizing a standardized set of reference images subjected to controlled distortions to assess algorithm performance. The paper provides examples of applying this approach to programs designed for boundary detection, restoration, and segmentation, key areas within computer image processing. The authors explore different methods, including those by Canny, Heitger, Rothwell, Black, Iverson, and Smith for boundary detection; Mumford–Shah, Geman–Reynolds, and piecewise linear function methods for image restoration; and EDISON, JSEG, EDGEFLOW, and MULTISCALE for segmentation. The study emphasizes the importance of reference images with known solutions, or ground truth, and introduces performance criteria like sensitivity and specificity. The report concludes by presenting results obtained using the proposed approach to assess the effectiveness of different program implementations in the context of blurring and noise. This comprehensive analysis offers valuable insights into the practical application and evaluation of image processing techniques.

ISSN 10546618, Pattern Recognition and Image Analysis, 2014, Vol. 24, No. 3, pp. 418–424. © Pleiades Publishing, Ltd., 2014.
1 1. INTRODUCTION
At present, digital image processing is the widest
research area involving both pure theoretical works
and worksdedicatedto solvingparticularapplied
problems. A great number of methods for solving dig
ital image processing problems such as recognition,
scene analysis, image understanding, segmentation,
and tracking have been developed. These methods, in
turn, have given rise to numerous algorithmic imple
mentations and, further, a great number of program
implementations of the algorithms. This process is
being continued. As a rule, such programs operate
efficiently only with allowance for particular condi
tions of their application and specific features of the
objects being processed. However, when changing the
conditions or specific features of the objects, the effi
ciency of the programs is sharply decreased. Moreover,
the existing universal methods, which are not based on
this allowance, always lose in application results to
problemoriented methods.
Whendesigningparticulartechnicalsystemsof
image processing, this situation gives rise to the prob
lem of choice. The latter consists in finding the most
efficient solution with respect to a particular problem
amonga greatnumberof readymadesolutions.
Below, the approach, which allows the program imple
mentation that is the most adequate to particular spec
ifications of a problem to be selected from the available
set of programimplementations,is demonstrated
using a number of digital image processing problems.
1 This article uses the materials of the report submitted at the 11th
InternationalConference“PatternRecognitionand Image
Analysis: New Information Technologies,” Samara, The Rus
sian Federation, September 23–28, 2013.
2. IMAGE PROCESSING PROBLEMS
AND SOLUTION METHODS
Let us first introduce a list of certain image process
ing problems and methods for their solution that are
used for testing the proposed approach. Problems of
boundary detection, restoration, and segmentation
are used as an example.
For the boundary detection problem, a number of
wellknown program implementations of the algo
rithms based on the methods by Canny [1], Heitg
[2], Rothwell [3], Black [4], Iverson [5], and Smith [6]
are used.Thesemethodsemployratherdifferent
approaches for solving the boundary detection prob
lem. In Canny’s method, socalled Canny filters are
used. Heitger’s method is based on simulating neuro
physiological processes of visual information process
ing. Rothwell’s method analyses the topological struc
ture of an image. Black’s method uses the anisotropic
diffusion equation. In Iverson’s method, the results of
using linear filters are processed using Boolean logic.
In Smith’s approach, the connected parts of an image
are found using nonlinear filtration.
The methods of Mumford–Shah [7] and Geman–
Reynolds [8] and the method with the piecewise linear
function in the performance functional [9] are used for
solving the image restoration problem. The image res
toration problem is stated as follows.
Let I(x, y) be the initial image defined in a certain
regionΩ(x, y) and letu(x, y) be the new restored initial
image, which is defined in the same region and is the
solution of the minimization problem with respect to
the functionalE that is generally called energy. The
above methods are distinguished by the energy func
tional used. The Mumford–Shah method uses the
functional of the following form:
where||∇u|| is the norm of the gradientu; λ, 0 <
λ <1, is the contribution of terms dependent onI
and on||∇u|| tor; andc is the additional normalization
E u( ) r
1 r+
, r
Ω
∫ 1 λ–( ) u I/c–( )2 λ ∇u 2,+= =
Direct Testing of Methods for Computer Image Pro1
P. P. Kol’tsov
Scientific Research Institute of System Analysis, Russian Academy of Sciences, Nakhimovskii pr. 36, korp. 1,
email: koltsov@niisi.msk.ru
Abstract—An empirical approach to estimating the performance of image processing programs based on
standardized set of references subjected to controlled distortions is proposed. Examples of appl
approach to programs for boundary detection, restoration, and segmentation are given.
Keywords: image processing, empirical method for algorithm estimation, blurring, noise, reference image
DOI:10.1134/S1054661814030109
Received December 30, 2013
REPRESENTATION, PROCESSING,
ANALYSIS AND UNDERSTANDING OF IMAGES
1 1. INTRODUCTION
At present, digital image processing is the widest
research area involving both pure theoretical works
and worksdedicatedto solvingparticularapplied
problems. A great number of methods for solving dig
ital image processing problems such as recognition,
scene analysis, image understanding, segmentation,
and tracking have been developed. These methods, in
turn, have given rise to numerous algorithmic imple
mentations and, further, a great number of program
implementations of the algorithms. This process is
being continued. As a rule, such programs operate
efficiently only with allowance for particular condi
tions of their application and specific features of the
objects being processed. However, when changing the
conditions or specific features of the objects, the effi
ciency of the programs is sharply decreased. Moreover,
the existing universal methods, which are not based on
this allowance, always lose in application results to
problemoriented methods.
Whendesigningparticulartechnicalsystemsof
image processing, this situation gives rise to the prob
lem of choice. The latter consists in finding the most
efficient solution with respect to a particular problem
amonga greatnumberof readymadesolutions.
Below, the approach, which allows the program imple
mentation that is the most adequate to particular spec
ifications of a problem to be selected from the available
set of programimplementations,is demonstrated
using a number of digital image processing problems.
1 This article uses the materials of the report submitted at the 11th
InternationalConference“PatternRecognitionand Image
Analysis: New Information Technologies,” Samara, The Rus
sian Federation, September 23–28, 2013.
2. IMAGE PROCESSING PROBLEMS
AND SOLUTION METHODS
Let us first introduce a list of certain image process
ing problems and methods for their solution that are
used for testing the proposed approach. Problems of
boundary detection, restoration, and segmentation
are used as an example.
For the boundary detection problem, a number of
wellknown program implementations of the algo
rithms based on the methods by Canny [1], Heitg
[2], Rothwell [3], Black [4], Iverson [5], and Smith [6]
are used.Thesemethodsemployratherdifferent
approaches for solving the boundary detection prob
lem. In Canny’s method, socalled Canny filters are
used. Heitger’s method is based on simulating neuro
physiological processes of visual information process
ing. Rothwell’s method analyses the topological struc
ture of an image. Black’s method uses the anisotropic
diffusion equation. In Iverson’s method, the results of
using linear filters are processed using Boolean logic.
In Smith’s approach, the connected parts of an image
are found using nonlinear filtration.
The methods of Mumford–Shah [7] and Geman–
Reynolds [8] and the method with the piecewise linear
function in the performance functional [9] are used for
solving the image restoration problem. The image res
toration problem is stated as follows.
Let I(x, y) be the initial image defined in a certain
regionΩ(x, y) and letu(x, y) be the new restored initial
image, which is defined in the same region and is the
solution of the minimization problem with respect to
the functionalE that is generally called energy. The
above methods are distinguished by the energy func
tional used. The Mumford–Shah method uses the
functional of the following form:
where||∇u|| is the norm of the gradientu; λ, 0 <
λ <1, is the contribution of terms dependent onI
and on||∇u|| tor; andc is the additional normalization
E u( ) r
1 r+
, r
Ω
∫ 1 λ–( ) u I/c–( )2 λ ∇u 2,+= =
Direct Testing of Methods for Computer Image Pro1
P. P. Kol’tsov
Scientific Research Institute of System Analysis, Russian Academy of Sciences, Nakhimovskii pr. 36, korp. 1,
email: koltsov@niisi.msk.ru
Abstract—An empirical approach to estimating the performance of image processing programs based on
standardized set of references subjected to controlled distortions is proposed. Examples of appl
approach to programs for boundary detection, restoration, and segmentation are given.
Keywords: image processing, empirical method for algorithm estimation, blurring, noise, reference image
DOI:10.1134/S1054661814030109
Received December 30, 2013
REPRESENTATION, PROCESSING,
ANALYSIS AND UNDERSTANDING OF IMAGES
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

PATTERN RECOGNITION AND IMAGE ANALYSIS Vol. 24 No. 3 2014
DIRECT TESTING OF METHODS FOR COMPUTER IMAGE PROCESSING 419
factor. The Geman–Reynolds uses the energy func
tional of the following form:
For the method with the piecewise linear function,
the functional is as follows:
whereϕ(r) is defined as follows
Program implementations of segmentation meth
ods (or segmenters) involve the following four well
E u( ) 1 λ–( ) u I–( )2 λ c2 ∇u 2
c2 ∇u 2
+
.
Ω
∫+
Ω
∫=
E u( ) 1 λ–( ) u I–( )2 λc2 ϕ ∇u /c( )2,
Ω
∫+
Ω
∫=
ϕ r( ) r, 0 r 1,≤ ≤
1, r 1.>⎩
⎨
⎧
=
known segmenters:EDISON [10], JSEG [11],
EDGEFLOW [12], and MULTISCALE [13]. The
EDISON segmenter implements the clusterization of
points satisfying the initial image on the feature space
The JSEG segmentercalculatesthe homogeneity
characteristic for each point of the transformed image
The EDGEFLOW segmenter forms the vector field of
the boundary point flow with region boundaries being
formed by integral curves of the field. The MULTI
SCALE segmenter also uses the boundary point flow
for image segmentation and boundary detection; how
ever, the vector field is generated for different exter
nally introduced scales.
3. REFERENCE IMAGES
Let us now consider the approach that allows the
results of applying different methods for solving th
same image processing problem to be compared. The
essence of the approach is rather simple. In order to
have comparable estimates of performance of differen
programs, it is required to have the opportunity t
compare the obtained solutions with exact ones. How
ever, the exact solution of the above image processing
problemsfor real objectsis, generallyspeaking,
unknown. In this case, it is proposed to compare the
performance of the programs using the images fo
which the exact solution is known in advance. Su
images are referred to as reference or test, while the
most accurate solution is known as the ground truth
solution or simply ground truth. Substantial require
ments on such images are as follows:
(1) the reference images must involve the fullest se
of the elements that are complex for the digital image
processing methods under study;
(2) for the comparative study of different image
processing programs, the reference images must allow
controlled distortions.
The process of creating the reference images is con
siderably unformalizable and is based on the experien
of using certain programs, which reveals the peculiarit
of their behavior over a wide range of images. Based o
this experience, the complex image elements and dist
tions, which have a considerable effect on the program
performance, can be discovered. It is these elements t
are to be used in designing reference images that wou
allow the introduction of distortions.
First, let us give the reference images used for com
paring the performance of the program implementa
tions of boundary detection algorithms. As is well
known, they are expected to provide a good preserva
tion of sudden jumps in brightness as well as noise sup
pression. Moreover, the complex case is the curvature
at boundaries and intersections, i.e., singular points.
Let us consider the aggregates of the points in th
plane that form boundaries (see Figs. 1–3).
These images can be regarded as a certain general
izationof the classicalclassificationof boundary
points.
Fig. 1.
Fig. 2.
Fig. 3.
DIRECT TESTING OF METHODS FOR COMPUTER IMAGE PROCESSING 419
factor. The Geman–Reynolds uses the energy func
tional of the following form:
For the method with the piecewise linear function,
the functional is as follows:
whereϕ(r) is defined as follows
Program implementations of segmentation meth
ods (or segmenters) involve the following four well
E u( ) 1 λ–( ) u I–( )2 λ c2 ∇u 2
c2 ∇u 2
+
.
Ω
∫+
Ω
∫=
E u( ) 1 λ–( ) u I–( )2 λc2 ϕ ∇u /c( )2,
Ω
∫+
Ω
∫=
ϕ r( ) r, 0 r 1,≤ ≤
1, r 1.>⎩
⎨
⎧
=
known segmenters:EDISON [10], JSEG [11],
EDGEFLOW [12], and MULTISCALE [13]. The
EDISON segmenter implements the clusterization of
points satisfying the initial image on the feature space
The JSEG segmentercalculatesthe homogeneity
characteristic for each point of the transformed image
The EDGEFLOW segmenter forms the vector field of
the boundary point flow with region boundaries being
formed by integral curves of the field. The MULTI
SCALE segmenter also uses the boundary point flow
for image segmentation and boundary detection; how
ever, the vector field is generated for different exter
nally introduced scales.
3. REFERENCE IMAGES
Let us now consider the approach that allows the
results of applying different methods for solving th
same image processing problem to be compared. The
essence of the approach is rather simple. In order to
have comparable estimates of performance of differen
programs, it is required to have the opportunity t
compare the obtained solutions with exact ones. How
ever, the exact solution of the above image processing
problemsfor real objectsis, generallyspeaking,
unknown. In this case, it is proposed to compare the
performance of the programs using the images fo
which the exact solution is known in advance. Su
images are referred to as reference or test, while the
most accurate solution is known as the ground truth
solution or simply ground truth. Substantial require
ments on such images are as follows:
(1) the reference images must involve the fullest se
of the elements that are complex for the digital image
processing methods under study;
(2) for the comparative study of different image
processing programs, the reference images must allow
controlled distortions.
The process of creating the reference images is con
siderably unformalizable and is based on the experien
of using certain programs, which reveals the peculiarit
of their behavior over a wide range of images. Based o
this experience, the complex image elements and dist
tions, which have a considerable effect on the program
performance, can be discovered. It is these elements t
are to be used in designing reference images that wou
allow the introduction of distortions.
First, let us give the reference images used for com
paring the performance of the program implementa
tions of boundary detection algorithms. As is well
known, they are expected to provide a good preserva
tion of sudden jumps in brightness as well as noise sup
pression. Moreover, the complex case is the curvature
at boundaries and intersections, i.e., singular points.
Let us consider the aggregates of the points in th
plane that form boundaries (see Figs. 1–3).
These images can be regarded as a certain general
izationof the classicalclassificationof boundary
points.
Fig. 1.
Fig. 2.
Fig. 3.

420
PATTERN RECOGNITION AND IMAGE ANALYSIS Vol. 24 No. 3 2014
KOL’TSOV
(1) A ledge is a point on different sides of which
intensities are considerably different.
(2) A break is a point in which the intensity deriva
tive has a ledge.
(3) A hump is a short segment such that the inten
sity within it differs considerably from the intensity
outside it (two adjacent ledges).
The ledge height, break angle, etc., are generally
taken as the parameters characterizing these points
(see figures). In Figs. 1 and 2, images have straight
boundaries with a linear variation of the height of
jumps in brightness along the vertical line and variable
thickness of the middle part. In Fig. 3, images have
variable curvature and a singular point. In all the
images, there is a wide spectrum of the conditions
affecting the performance of the boundary detection
program, which allows one to obtain its operating
results under different conditions during a run while
revealing the peculiarities of the studied program
well as the limits of its applicability. The noise an
blurring commonly encountered in actual practice are
appropriate for use as distortions of the references.
The above reference images are also applicable in
image restoration problems with the preservation
sudden jumps in brightness as well as noise suppressio
being required and complex situations being the same
For the same reasons, these images are suitable for th
case of studying the performance of segmentation
algorithms; however, they require reinforcement with
the angles,low object/backgroundcontrast,and
Fig. 4.
Fig. 5.
Fig. 6.
PATTERN RECOGNITION AND IMAGE ANALYSIS Vol. 24 No. 3 2014
KOL’TSOV
(1) A ledge is a point on different sides of which
intensities are considerably different.
(2) A break is a point in which the intensity deriva
tive has a ledge.
(3) A hump is a short segment such that the inten
sity within it differs considerably from the intensity
outside it (two adjacent ledges).
The ledge height, break angle, etc., are generally
taken as the parameters characterizing these points
(see figures). In Figs. 1 and 2, images have straight
boundaries with a linear variation of the height of
jumps in brightness along the vertical line and variable
thickness of the middle part. In Fig. 3, images have
variable curvature and a singular point. In all the
images, there is a wide spectrum of the conditions
affecting the performance of the boundary detection
program, which allows one to obtain its operating
results under different conditions during a run while
revealing the peculiarities of the studied program
well as the limits of its applicability. The noise an
blurring commonly encountered in actual practice are
appropriate for use as distortions of the references.
The above reference images are also applicable in
image restoration problems with the preservation
sudden jumps in brightness as well as noise suppressio
being required and complex situations being the same
For the same reasons, these images are suitable for th
case of studying the performance of segmentation
algorithms; however, they require reinforcement with
the angles,low object/backgroundcontrast,and
Fig. 4.
Fig. 5.
Fig. 6.
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
PATTERN RECOGNITION AND IMAGE ANALYSIS Vol. 24 No. 3 2014
DIRECT TESTING OF METHODS FOR COMPUTER IMAGE PROCESSING 421
smoothvariationof brightness(falseboundaries)
being complex cases for the programs. In order to take
these cases into account, the reference images shown
in Figs. 4–6 are used.
Note that the given set of reference images is open
and can be supplementedwith otherimagesthat
involve elements typical for particular conditions of
solving image processing problems.
4. PERFORMANCE CRITERIA
The distance between the exact solution and the
solution provided by the program, the statistical char
acteristics of the solution accuracy, or other measur
able values fixing the dissimilarity between the pro
gram result and the ground truth can be used as the
performance criterion for the image processing pro
gram. Note that the choice of different performance
criteriaincludingparticularmetricsallowsa wide
spectrum of behavioral features of the compared pro
grams to be revealed. When using the Euclidean dis
tance as a disparity measure between the ground truth
and the program result, a certain average value of the
disparity with respect to the entire image will obvi
ously be obtained. In the case of using the Hausdorff
metric, even visually small differences between the
ground truth and the program result have a strong
effect on the result. The sensitivity and specificity
indexes can be used as a statistical characteristic of the
accuracy of solving the image processing problem.
The sensitivity is the portion of ground truth pixels in
the solution of the problem using the program with
respect to all ground truth pixels, while the specificity
is the portion of ground truth pixels among all the pix
els of the problem solution.
5. RESULTS OF COMPARING
THE PROGRAM IMPLEMENTATIONS
Let us now present the results obtained using the
proposed approach to estimating the performance of
different program implementations of the algorithms
for solving the above three image processing problems.
For the boundary detection problem, the sensitiv
ity and specificity indexes are taken as quality criteria
Distortions are introduced in the form of blurring and
noise.
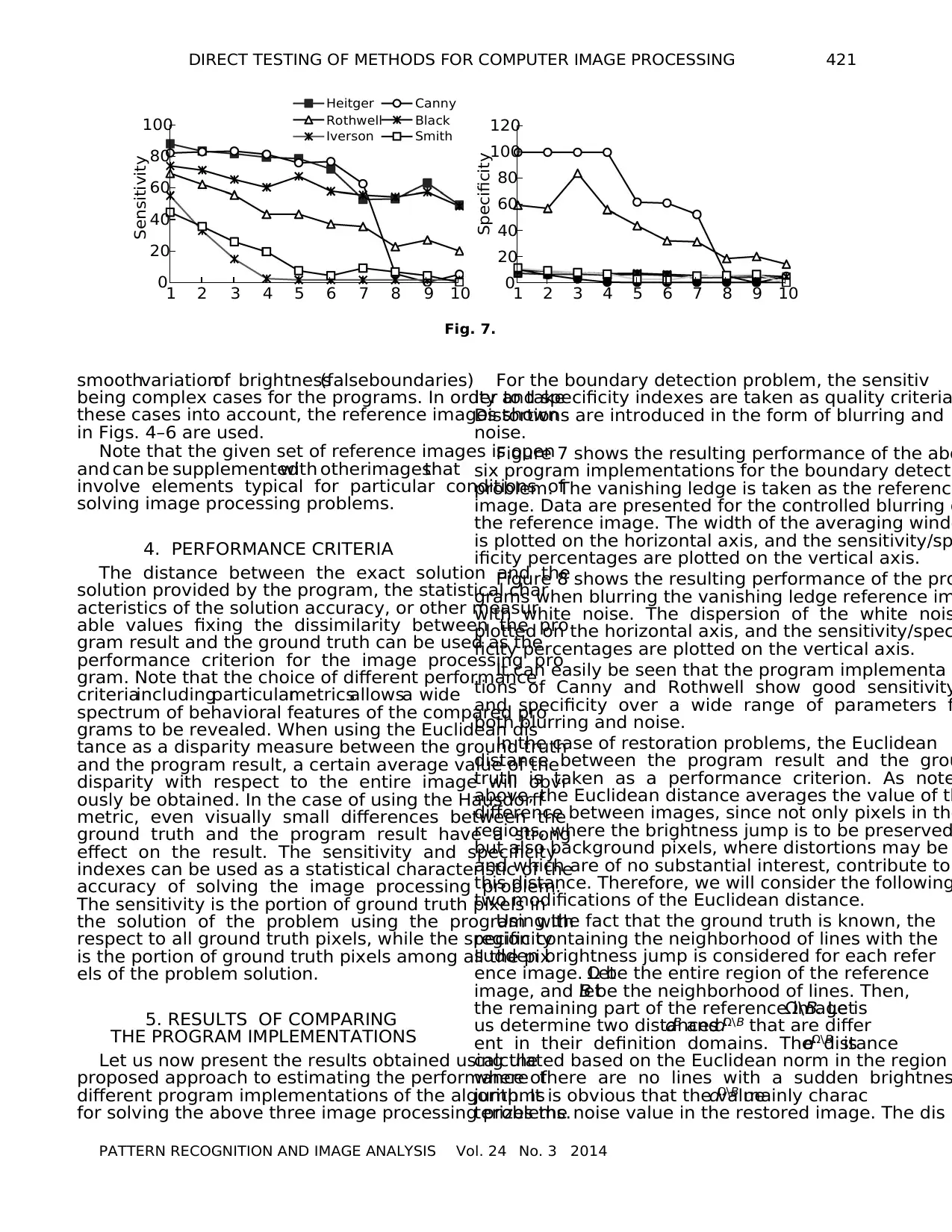
Figure 7 shows the resulting performance of the abo
six program implementations for the boundary detecti
problem. The vanishing ledge is taken as the reference
image. Data are presented for the controlled blurring o
the reference image. The width of the averaging windo
is plotted on the horizontal axis, and the sensitivity/sp
ificity percentages are plotted on the vertical axis.
Figure 8 shows the resulting performance of the pro
grams when blurring the vanishing ledge reference im
with white noise. The dispersion of the white nois
plotted on the horizontal axis, and the sensitivity/spec
ficity percentages are plotted on the vertical axis.
It can easily be seen that the program implementa
tions of Canny and Rothwell show good sensitivity
and specificity over a wide range of parameters f
both blurring and noise.
In the case of restoration problems, the Euclidean
distance between the program result and the grou
truth is taken as a performance criterion. As note
above, the Euclidean distance averages the value of th
difference between images, since not only pixels in the
regions, where the brightness jump is to be preserved
but also background pixels, where distortions may be
and which are of no substantial interest, contribute to
this distance. Therefore, we will consider the following
two modifications of the Euclidean distance.
Using the fact that the ground truth is known, the
region containing the neighborhood of lines with the
sudden brightness jump is considered for each refer
ence image. LetΩ be the entire region of the reference
image, and letB be the neighborhood of lines. Then,
the remaining part of the reference image isΩ \B. Let
us determine two distancesdB anddΩ \B that are differ
ent in their definition domains. The distancedΩ\B is
calculated based on the Euclidean norm in the region
where there are no lines with a sudden brightnes
jump. It is obvious that the valuedΩ\B mainly charac
terizes the noise value in the restored image. The dis
100
80
60
40
20
01 2 3 4 5 6 7 8 9 10
Sensitivity
Heitger
Rothwell
Iverson
Canny
Black
Smith 120
100
80
60
40
20
01 2 3 4 5 6 7 8 9 10
Specificity
Fig. 7.
DIRECT TESTING OF METHODS FOR COMPUTER IMAGE PROCESSING 421
smoothvariationof brightness(falseboundaries)
being complex cases for the programs. In order to take
these cases into account, the reference images shown
in Figs. 4–6 are used.
Note that the given set of reference images is open
and can be supplementedwith otherimagesthat
involve elements typical for particular conditions of
solving image processing problems.
4. PERFORMANCE CRITERIA
The distance between the exact solution and the
solution provided by the program, the statistical char
acteristics of the solution accuracy, or other measur
able values fixing the dissimilarity between the pro
gram result and the ground truth can be used as the
performance criterion for the image processing pro
gram. Note that the choice of different performance
criteriaincludingparticularmetricsallowsa wide
spectrum of behavioral features of the compared pro
grams to be revealed. When using the Euclidean dis
tance as a disparity measure between the ground truth
and the program result, a certain average value of the
disparity with respect to the entire image will obvi
ously be obtained. In the case of using the Hausdorff
metric, even visually small differences between the
ground truth and the program result have a strong
effect on the result. The sensitivity and specificity
indexes can be used as a statistical characteristic of the
accuracy of solving the image processing problem.
The sensitivity is the portion of ground truth pixels in
the solution of the problem using the program with
respect to all ground truth pixels, while the specificity
is the portion of ground truth pixels among all the pix
els of the problem solution.
5. RESULTS OF COMPARING
THE PROGRAM IMPLEMENTATIONS
Let us now present the results obtained using the
proposed approach to estimating the performance of
different program implementations of the algorithms
for solving the above three image processing problems.
For the boundary detection problem, the sensitiv
ity and specificity indexes are taken as quality criteria
Distortions are introduced in the form of blurring and
noise.
Figure 7 shows the resulting performance of the abo
six program implementations for the boundary detecti
problem. The vanishing ledge is taken as the reference
image. Data are presented for the controlled blurring o
the reference image. The width of the averaging windo
is plotted on the horizontal axis, and the sensitivity/sp
ificity percentages are plotted on the vertical axis.
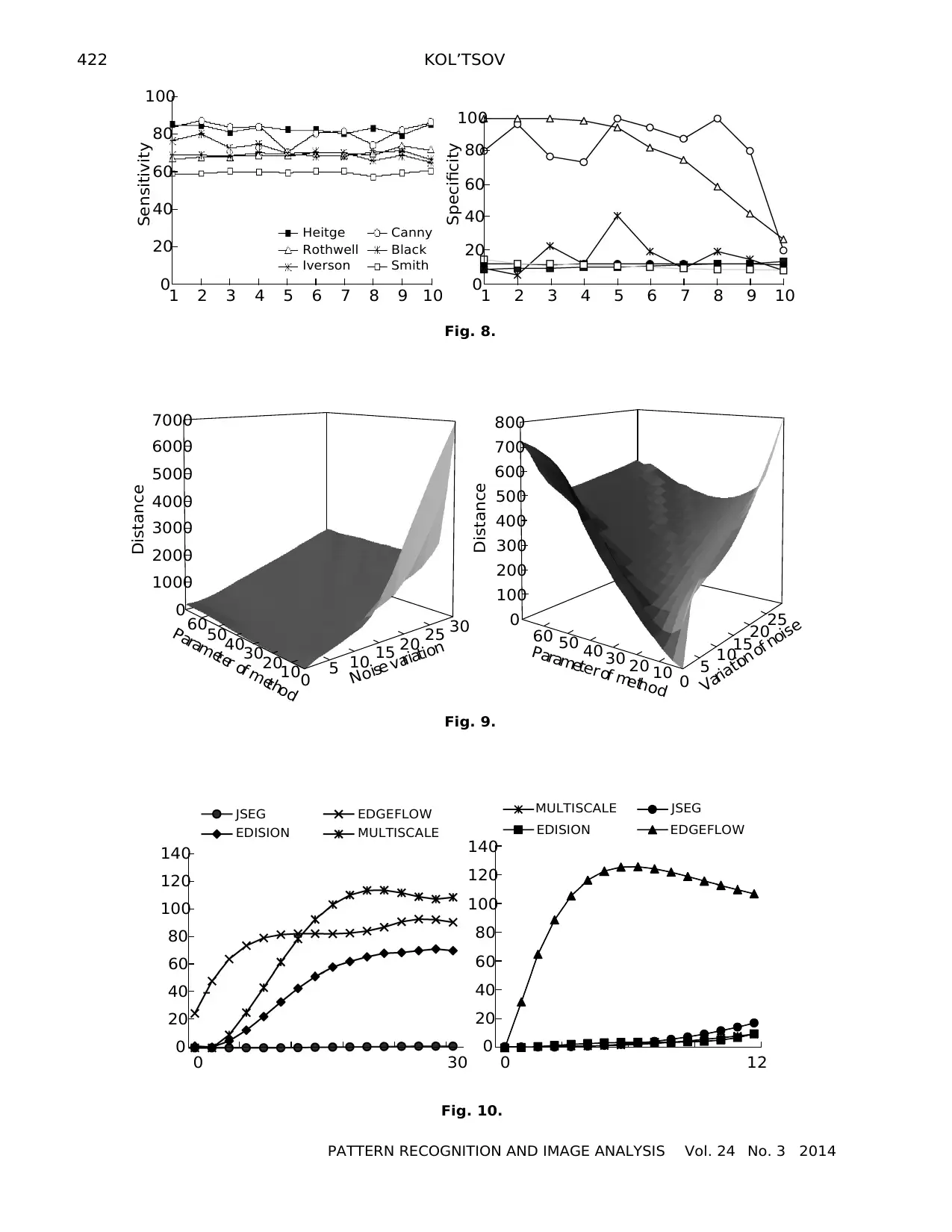
Figure 8 shows the resulting performance of the pro
grams when blurring the vanishing ledge reference im
with white noise. The dispersion of the white nois
plotted on the horizontal axis, and the sensitivity/spec
ficity percentages are plotted on the vertical axis.
It can easily be seen that the program implementa
tions of Canny and Rothwell show good sensitivity
and specificity over a wide range of parameters f
both blurring and noise.
In the case of restoration problems, the Euclidean
distance between the program result and the grou
truth is taken as a performance criterion. As note
above, the Euclidean distance averages the value of th
difference between images, since not only pixels in the
regions, where the brightness jump is to be preserved
but also background pixels, where distortions may be
and which are of no substantial interest, contribute to
this distance. Therefore, we will consider the following
two modifications of the Euclidean distance.
Using the fact that the ground truth is known, the
region containing the neighborhood of lines with the
sudden brightness jump is considered for each refer
ence image. LetΩ be the entire region of the reference
image, and letB be the neighborhood of lines. Then,
the remaining part of the reference image isΩ \B. Let
us determine two distancesdB anddΩ \B that are differ
ent in their definition domains. The distancedΩ\B is
calculated based on the Euclidean norm in the region
where there are no lines with a sudden brightnes
jump. It is obvious that the valuedΩ\B mainly charac
terizes the noise value in the restored image. The dis
100
80
60
40
20
01 2 3 4 5 6 7 8 9 10
Sensitivity
Heitger
Rothwell
Iverson
Canny
Black
Smith 120
100
80
60
40
20
01 2 3 4 5 6 7 8 9 10
Specificity
Fig. 7.
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
422
PATTERN RECOGNITION AND IMAGE ANALYSIS Vol. 24 No. 3 2014
KOL’TSOV
100
80
60
40
20
01 2 3 4 5 6 7 8 9 10
Sensitivity
Heitge
Rothwell
Iverson
Canny
Black
Smith
100
80
60
40
20
01 2 3 4 5 6 7 8 9 10
Specificity
Fig. 8.
6050403020100 5 10 15 20 25 30
1000
0
2000
3000
4000
5000
6000
7000
Distance
Parameter of method
Noise variation
800
700
600
500
400
300
200
100
0
60 50 40 30 20 10 0 5 10
15
2025
Distance
Parameter of method
Variation of noise
Fig. 9.
140
120
100
80
60
40
20
0 0 30
140
120
100
80
60
40
20
0
0 12
JSEG
EDISION
EDGEFLOW
MULTISCALE
MULTISCALE
EDGEFLOW
JSEG
EDISION
Fig. 10.
PATTERN RECOGNITION AND IMAGE ANALYSIS Vol. 24 No. 3 2014
KOL’TSOV
100
80
60
40
20
01 2 3 4 5 6 7 8 9 10
Sensitivity
Heitge
Rothwell
Iverson
Canny
Black
Smith
100
80
60
40
20
01 2 3 4 5 6 7 8 9 10
Specificity
Fig. 8.
6050403020100 5 10 15 20 25 30
1000
0
2000
3000
4000
5000
6000
7000
Distance
Parameter of method
Noise variation
800
700
600
500
400
300
200
100
0
60 50 40 30 20 10 0 5 10
15
2025
Distance
Parameter of method
Variation of noise
Fig. 9.
140
120
100
80
60
40
20
0 0 30
140
120
100
80
60
40
20
0
0 12
JSEG
EDISION
EDGEFLOW
MULTISCALE
MULTISCALE
EDGEFLOW
JSEG
EDISION
Fig. 10.

PATTERN RECOGNITION AND IMAGE ANALYSIS Vol. 24 No. 3 2014
DIRECT TESTING OF METHODS FOR COMPUTER IMAGE PROCESSING 423
tancedB is calculated based on the Euclidean norm in
the regionwherethereare lineswith the sudden
brightness jump. Obviously, the valuedB is great if the
lines in the restored image are blurred and is small if
sudden brightness jumps are preserved. These two dis
tances are used as performance criteria for the image
restoration programs.
Figure 9 shows the distances between the image
restored after noising and the varying hump II initial
reference image for regionsΩ\B andB. The implemen
tation of the Mumford–Shah method is used to solve
the restoration problem. The left chart is given for the
regionΩ\B, while the right chart is for the regionB.
It can be seen (left chart) that the noise suppression
slumps for great noise values. The sudden brightness
jumps are confidently preserved for low noise values
(see right chart).
In the case of the segmentation problem, the Haus
dorff distance is used to estimate the performance of
the segmenters. The results obtained for the reference
imageswith angles,lowcontrastboundaries,and
smoothly varying brightness are shown in Fig. 10. Data
for the Gaussian noise are presented from the left,
while data for the blurring are from the right. The
advantage of the JSEG segmenter as compared to the
other segmenters for the noising as well as a sharp dif
ference in the performance of the EDGEFLOW seg
menter as compared to the other segmenters for the
blurring can be seen. The data are averaged with
respect to all the reference images.
The examples of using the set of reference images
show the capabilities of the proposed approach to esti
matingthe performanceof differentprogramsfor
solving a particular image processing problem. The
introduction of distortions allows the estimates to be
obtained for particular external conditions that are the
most adequate for the problem solved.
6. CONCLUSIONS
In addition to the above image processing prob
lems, the performance of a number of wellknown
programs for solving problems of textural analysis,
boundary refinement, boundary detection using the
socalled energy methods, and affine transform of ini
tial images has successfully been estimated within the
framework of the proposed approach. Besides classical
metrics and their modifications, fuzzy metrics [14] are
used as the measure of proximity of the obtained solu
tions to the ground truth. The results provide specific
recommendations for using certain program imple
mentations of digital image processing algorithms.
These largescale studies have required the creation of
a specialpurposetool environmentwhich was
designed in SRISA/NIISI RAS and involves the two
followingsystems:PICASSO (PICture Algorithms
Study SOftware) and PETRA (Performance Evalua
tion of Texture Recognition Algorithms) [15–17]. The
team of researchers that carried out the above work
involved I.V. Gribkov, A.V. Zakharov, M.V. Koganov,
N.V. Kotovich, A.A Kravchenko,A.S. Kutsaev,
V.K. Nikolaev, and A.S. Osipov.
Thus,the proposedapproachallowscomparable
estimatesof the performanceof differentprogram
implementations of image processing algorithms to be
obtained. The approach is based on the informal con
struction of a fixed set of reference images used for di
comparison of different image processing programs. T
obtained quality estimates are universal in terms of pr
viding the comparison of the performance of program
implementations of a wide range of image proces
methods based on considerably different models. Obv
ously, such an approach, which is called the direct tes
ing of methods for computer image processing, can be
used in other application fields associated with solving
applied problems using data processing.
REFERENCES
1. J. A. Canny, “Computational approach to edge detec
tion,” IEEE Pattern Anal. Machin. Intell.8 (16), 679–
698 (1986).
2. E. Heitger, L. Rosenthaler, R. von der Heydt, E. Peter
hans, and O. Kubler, “Simulation of neural contour
mechanisms: from simple to endstopped cells,” Vision
Res., No. 32, 963–981 (1992).
3. C. A. Rothwell, J. L. Mundy, W. Hoffman, et al., “Driv
ing vision by topology,” inProc. Int. Symp. on Computer
Vision(Coral Gables, FL, 1995), pp. 395–400.
4. M. Black, G. Sapiro, D. Marimont, et al., “Robust
anisotropic diffusion,” IEEE Trans. Image Process.7
(3), 421–432 (1998).
5. L. A. Iverson and S. W. Zucker, “Logical/linear opera
tors for imagecurves,”IEEE Trans.PatternAnal.
Mach. Intell.17(10), 982–996 (1999).
6. S. M. Smith, “Flexible filter neighborhood designa
tion,” inProc. 13th Int. Conf. on Pattern Recognition
(Vienna, 1996), Vol. 1, pp. 206–212.
7. D. Mumford and J. Shah, “Optimal approximations by
piecewise smooth functions and associated variational
problems,” Commun. Pure Appl. Math.52, 577–685
(1989).
8. D. Geman and G. Reynolds, “Constrained restoration
and the recovery of discontinuities,” IEEE TPAMI14,
376–383 (1992).
9. O. Veksler, “Efficient graphbased energy minimization
methods in computer vision,” PhD Thesis (Cornell
Univ., 1999).
10.C. M. Christoudias, B. Georgescu, et al., “Synergism
in low level vision,” inProc. 16th Int. Conf. on Pattern
Recognition(2002), Vol. 4, pp. 150–155.
11.Y. Deng and B. S. Manjunath, “Unsupervised segmen
tation of colortexture regions in images and video,”
IEEE Trans. Pattern Anal. Mach. Intellig. (PAMI’01)
23(8), 800–810 (2001).
12.W.Y. Ma and B. S. Manjunath, “EdgeFlow: a technique
for boundary detection and image segmentation,” IEEE
Trans. Image Processing9, 1375–1388 (2002).
DIRECT TESTING OF METHODS FOR COMPUTER IMAGE PROCESSING 423
tancedB is calculated based on the Euclidean norm in
the regionwherethereare lineswith the sudden
brightness jump. Obviously, the valuedB is great if the
lines in the restored image are blurred and is small if
sudden brightness jumps are preserved. These two dis
tances are used as performance criteria for the image
restoration programs.
Figure 9 shows the distances between the image
restored after noising and the varying hump II initial
reference image for regionsΩ\B andB. The implemen
tation of the Mumford–Shah method is used to solve
the restoration problem. The left chart is given for the
regionΩ\B, while the right chart is for the regionB.
It can be seen (left chart) that the noise suppression
slumps for great noise values. The sudden brightness
jumps are confidently preserved for low noise values
(see right chart).
In the case of the segmentation problem, the Haus
dorff distance is used to estimate the performance of
the segmenters. The results obtained for the reference
imageswith angles,lowcontrastboundaries,and
smoothly varying brightness are shown in Fig. 10. Data
for the Gaussian noise are presented from the left,
while data for the blurring are from the right. The
advantage of the JSEG segmenter as compared to the
other segmenters for the noising as well as a sharp dif
ference in the performance of the EDGEFLOW seg
menter as compared to the other segmenters for the
blurring can be seen. The data are averaged with
respect to all the reference images.
The examples of using the set of reference images
show the capabilities of the proposed approach to esti
matingthe performanceof differentprogramsfor
solving a particular image processing problem. The
introduction of distortions allows the estimates to be
obtained for particular external conditions that are the
most adequate for the problem solved.
6. CONCLUSIONS
In addition to the above image processing prob
lems, the performance of a number of wellknown
programs for solving problems of textural analysis,
boundary refinement, boundary detection using the
socalled energy methods, and affine transform of ini
tial images has successfully been estimated within the
framework of the proposed approach. Besides classical
metrics and their modifications, fuzzy metrics [14] are
used as the measure of proximity of the obtained solu
tions to the ground truth. The results provide specific
recommendations for using certain program imple
mentations of digital image processing algorithms.
These largescale studies have required the creation of
a specialpurposetool environmentwhich was
designed in SRISA/NIISI RAS and involves the two
followingsystems:PICASSO (PICture Algorithms
Study SOftware) and PETRA (Performance Evalua
tion of Texture Recognition Algorithms) [15–17]. The
team of researchers that carried out the above work
involved I.V. Gribkov, A.V. Zakharov, M.V. Koganov,
N.V. Kotovich, A.A Kravchenko,A.S. Kutsaev,
V.K. Nikolaev, and A.S. Osipov.
Thus,the proposedapproachallowscomparable
estimatesof the performanceof differentprogram
implementations of image processing algorithms to be
obtained. The approach is based on the informal con
struction of a fixed set of reference images used for di
comparison of different image processing programs. T
obtained quality estimates are universal in terms of pr
viding the comparison of the performance of program
implementations of a wide range of image proces
methods based on considerably different models. Obv
ously, such an approach, which is called the direct tes
ing of methods for computer image processing, can be
used in other application fields associated with solving
applied problems using data processing.
REFERENCES
1. J. A. Canny, “Computational approach to edge detec
tion,” IEEE Pattern Anal. Machin. Intell.8 (16), 679–
698 (1986).
2. E. Heitger, L. Rosenthaler, R. von der Heydt, E. Peter
hans, and O. Kubler, “Simulation of neural contour
mechanisms: from simple to endstopped cells,” Vision
Res., No. 32, 963–981 (1992).
3. C. A. Rothwell, J. L. Mundy, W. Hoffman, et al., “Driv
ing vision by topology,” inProc. Int. Symp. on Computer
Vision(Coral Gables, FL, 1995), pp. 395–400.
4. M. Black, G. Sapiro, D. Marimont, et al., “Robust
anisotropic diffusion,” IEEE Trans. Image Process.7
(3), 421–432 (1998).
5. L. A. Iverson and S. W. Zucker, “Logical/linear opera
tors for imagecurves,”IEEE Trans.PatternAnal.
Mach. Intell.17(10), 982–996 (1999).
6. S. M. Smith, “Flexible filter neighborhood designa
tion,” inProc. 13th Int. Conf. on Pattern Recognition
(Vienna, 1996), Vol. 1, pp. 206–212.
7. D. Mumford and J. Shah, “Optimal approximations by
piecewise smooth functions and associated variational
problems,” Commun. Pure Appl. Math.52, 577–685
(1989).
8. D. Geman and G. Reynolds, “Constrained restoration
and the recovery of discontinuities,” IEEE TPAMI14,
376–383 (1992).
9. O. Veksler, “Efficient graphbased energy minimization
methods in computer vision,” PhD Thesis (Cornell
Univ., 1999).
10.C. M. Christoudias, B. Georgescu, et al., “Synergism
in low level vision,” inProc. 16th Int. Conf. on Pattern
Recognition(2002), Vol. 4, pp. 150–155.
11.Y. Deng and B. S. Manjunath, “Unsupervised segmen
tation of colortexture regions in images and video,”
IEEE Trans. Pattern Anal. Mach. Intellig. (PAMI’01)
23(8), 800–810 (2001).
12.W.Y. Ma and B. S. Manjunath, “EdgeFlow: a technique
for boundary detection and image segmentation,” IEEE
Trans. Image Processing9, 1375–1388 (2002).
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

424
PATTERN RECOGNITION AND IMAGE ANALYSIS Vol. 24 No. 3 2014
KOL’TSOV
13.B. Sumengen and B. S. Manjunath, “Multiscale edge
detection and image segmentation,” inProc. European
Signal Processing Conf. (EUSIPCO)(Antalya, 2005),
Vol. CD. http://vision.ece.ucsb.edu/publications/
05eusipcoBarisMultiscale.pdf
14.G. Jäger and U. Benz, “Measures of classification
accuracybasedon fuzzy similarity,”IEEE Trans.
Geosci. Remote Sensing38(3), 1462–1467 (2000).
15.I. V. Gribkov, P. P. Koltsov, N. V. Kotovich,
A. A. Kravchenko, A. S. Koutsaev, A. S. Osipov, and
A. V. Zakharov, “PICASSO—A system for evaluating
edge detectors algorithms,” Pattern Recogn. Image
Anal.13(4), 617–622 (2003).
16.I. V. Gribkov,P. P. Koltsov,N. V. Kotovich,
A. A. Kravchenko, A. S. Koutsaev, V. K. Nikolaev, and
A. V. Zakharov, “Performance evaluation of texture seg
mentation methods,” inProc. 13th World MultiConf. on
Systemics,Cybernetics,and Informatics(Orlando,
2009), Vol. 4, pp. 137–142.
17.I. V. Gribkov,P. P. Koltsov,N. V. Kotovich,
A. A. Kravchenko, A. S. Koutsaev, V. K. Nikolaev, and
A. V. Zakharov, “Affine invariance study of edge detec
tion algorithms by means of PICASSO 2 system,” in
Proc. 6th WSEAS Int. Conf. on Signal, Speech, and
Image Processing(Madrid, 2006), pp. 11–16.
Translated by Yu. Kornienko
Petr PetrovichKol’tsov.Born
1946. Graduated from the Moscow
Institute of Physics and Technology
in 1971. Received candidate’s
degree in mathematical cybernetics
in 1975 and doctoral degree in theo
retical informatics in 2012. Deputy
Director for Research of the Scien
tific ResearchInstituteof System
Analysis, Russian Academy of Sci
ences.Author of more than 80
papers.Memberof the National
Committee of the RAS on pattern recognition and image
analysis. Winner of state awards for research and technol
ogy achievements.
PATTERN RECOGNITION AND IMAGE ANALYSIS Vol. 24 No. 3 2014
KOL’TSOV
13.B. Sumengen and B. S. Manjunath, “Multiscale edge
detection and image segmentation,” inProc. European
Signal Processing Conf. (EUSIPCO)(Antalya, 2005),
Vol. CD. http://vision.ece.ucsb.edu/publications/
05eusipcoBarisMultiscale.pdf
14.G. Jäger and U. Benz, “Measures of classification
accuracybasedon fuzzy similarity,”IEEE Trans.
Geosci. Remote Sensing38(3), 1462–1467 (2000).
15.I. V. Gribkov, P. P. Koltsov, N. V. Kotovich,
A. A. Kravchenko, A. S. Koutsaev, A. S. Osipov, and
A. V. Zakharov, “PICASSO—A system for evaluating
edge detectors algorithms,” Pattern Recogn. Image
Anal.13(4), 617–622 (2003).
16.I. V. Gribkov,P. P. Koltsov,N. V. Kotovich,
A. A. Kravchenko, A. S. Koutsaev, V. K. Nikolaev, and
A. V. Zakharov, “Performance evaluation of texture seg
mentation methods,” inProc. 13th World MultiConf. on
Systemics,Cybernetics,and Informatics(Orlando,
2009), Vol. 4, pp. 137–142.
17.I. V. Gribkov,P. P. Koltsov,N. V. Kotovich,
A. A. Kravchenko, A. S. Koutsaev, V. K. Nikolaev, and
A. V. Zakharov, “Affine invariance study of edge detec
tion algorithms by means of PICASSO 2 system,” in
Proc. 6th WSEAS Int. Conf. on Signal, Speech, and
Image Processing(Madrid, 2006), pp. 11–16.
Translated by Yu. Kornienko
Petr PetrovichKol’tsov.Born
1946. Graduated from the Moscow
Institute of Physics and Technology
in 1971. Received candidate’s
degree in mathematical cybernetics
in 1975 and doctoral degree in theo
retical informatics in 2012. Deputy
Director for Research of the Scien
tific ResearchInstituteof System
Analysis, Russian Academy of Sci
ences.Author of more than 80
papers.Memberof the National
Committee of the RAS on pattern recognition and image
analysis. Winner of state awards for research and technol
ogy achievements.
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

Reproduced with permission of the copyright owner. Further reproduction prohibited withou
permission.
permission.
1 out of 8
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
Copyright © 2020–2026 A2Z Services. All Rights Reserved. Developed and managed by ZUCOL.
