Risk Management in Projects
VerifiedAdded on 2023/03/17
|11
|2238
|71
AI Summary
This document discusses risk management in projects, focusing on bid pricing, probability calculations, Bayes rule, production scheduling, and project risk exposure. It provides insights into making informed decisions and optimizing profitability.
Contribute Materials
Your contribution can guide someone’s learning journey. Share your
documents today.

Risk management in Projects
Secure Best Marks with AI Grader
Need help grading? Try our AI Grader for instant feedback on your assignments.

Question 1
Introduction to the Problem
ABC Computer Company (hereinafter known just as ABC) is considering bidding to supply 10,000
specialized computers to the government for use in computer aided design; however, thee is
another potential bidder, Complex Computers Inc (hereinafter known as Complex). ABC is faced
with a challenge; at present the company is working on a new process for production that has not
been tested, but which can potentially reduce the cost of the computers significantly. There is also a
chance the new process, having not been tested, can become even more expensive compared to the
present process and the dilemma is that ABC cannot determine the cost of production using the new
process without actually trying it out. To bid for the supply contract, there are three possible bids: $
9500, $ 8500, and $ 7500 per computer. It is certain that Complex will also bid at prices of $ 10000,
$ 9000, and $ 8000 per computer and bidding will offset ABC $ one million regardless of whether
they win the contract or not (this is bidding preparation cost). The current production process costs
$ 8000 for ABC to produce the computers while with the new process, the probability of
manufacturing each computer at $ 5000 is 0.25; the probability of doing so at $ 7500 is 0.50, and
the probability of producing at $ 8500 is 0.25. The dilemma is whether ABC should bid for the
contract and at what price?
Decisions Tree Without EMV
This was developed as shown below;
Introduction to the Problem
ABC Computer Company (hereinafter known just as ABC) is considering bidding to supply 10,000
specialized computers to the government for use in computer aided design; however, thee is
another potential bidder, Complex Computers Inc (hereinafter known as Complex). ABC is faced
with a challenge; at present the company is working on a new process for production that has not
been tested, but which can potentially reduce the cost of the computers significantly. There is also a
chance the new process, having not been tested, can become even more expensive compared to the
present process and the dilemma is that ABC cannot determine the cost of production using the new
process without actually trying it out. To bid for the supply contract, there are three possible bids: $
9500, $ 8500, and $ 7500 per computer. It is certain that Complex will also bid at prices of $ 10000,
$ 9000, and $ 8000 per computer and bidding will offset ABC $ one million regardless of whether
they win the contract or not (this is bidding preparation cost). The current production process costs
$ 8000 for ABC to produce the computers while with the new process, the probability of
manufacturing each computer at $ 5000 is 0.25; the probability of doing so at $ 7500 is 0.50, and
the probability of producing at $ 8500 is 0.25. The dilemma is whether ABC should bid for the
contract and at what price?
Decisions Tree Without EMV
This was developed as shown below;
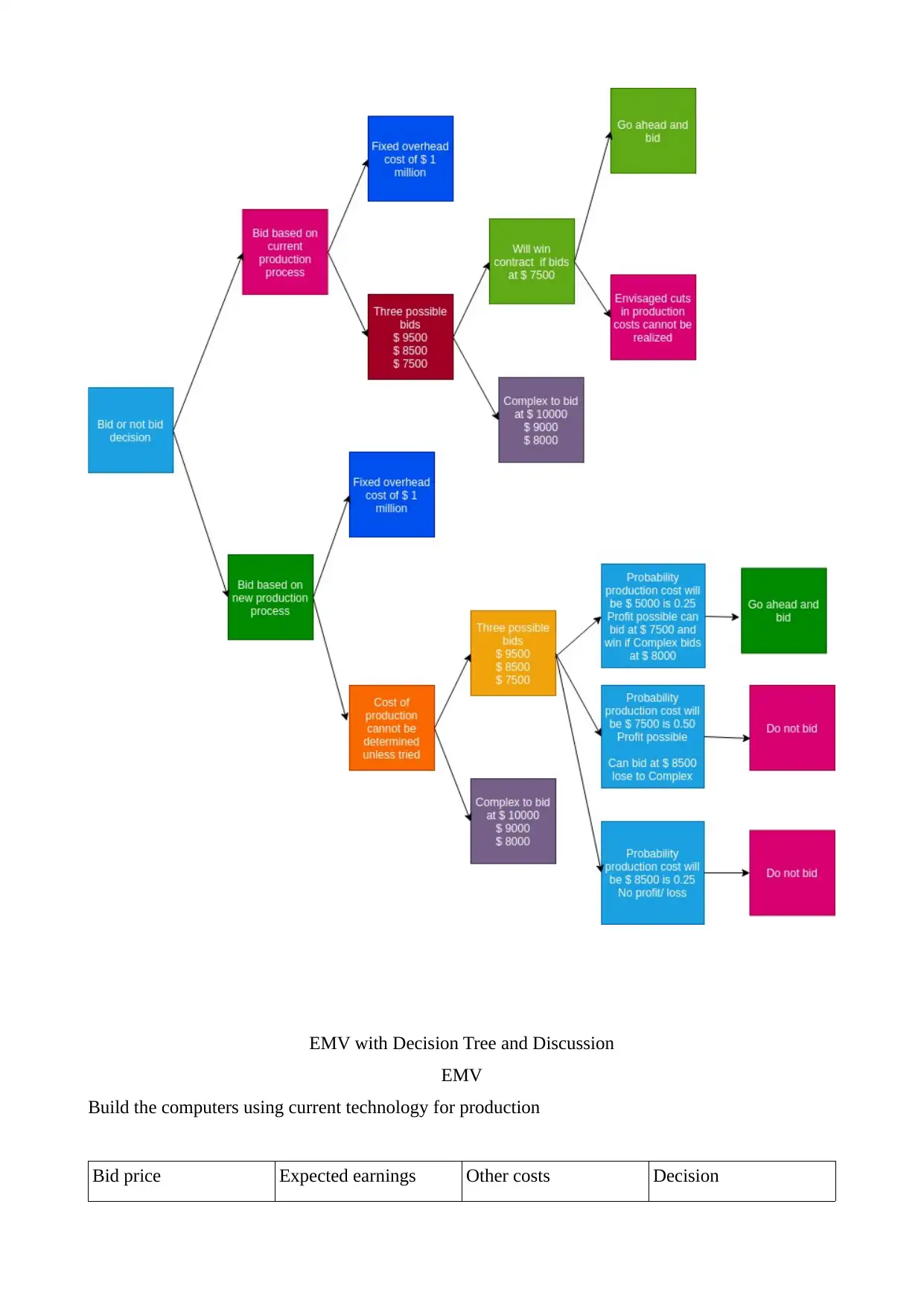
EMV with Decision Tree and Discussion
EMV
Build the computers using current technology for production
Bid price Expected earnings Other costs Decision
EMV
Build the computers using current technology for production
Bid price Expected earnings Other costs Decision
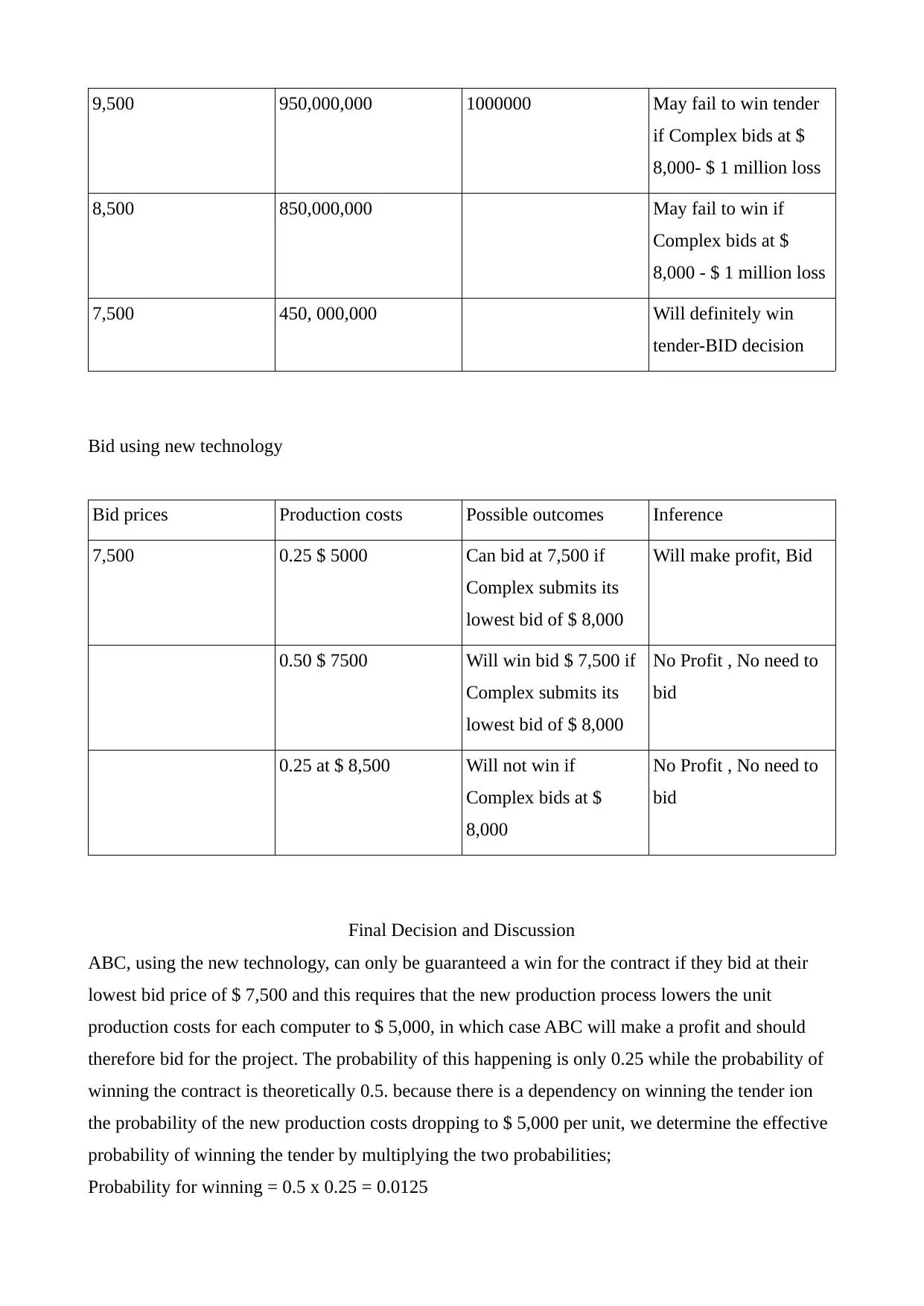
9,500 950,000,000 1000000 May fail to win tender
if Complex bids at $
8,000- $ 1 million loss
8,500 850,000,000 May fail to win if
Complex bids at $
8,000 - $ 1 million loss
7,500 450, 000,000 Will definitely win
tender-BID decision
Bid using new technology
Bid prices Production costs Possible outcomes Inference
7,500 0.25 $ 5000 Can bid at 7,500 if
Complex submits its
lowest bid of $ 8,000
Will make profit, Bid
0.50 $ 7500 Will win bid $ 7,500 if
Complex submits its
lowest bid of $ 8,000
No Profit , No need to
bid
0.25 at $ 8,500 Will not win if
Complex bids at $
8,000
No Profit , No need to
bid
Final Decision and Discussion
ABC, using the new technology, can only be guaranteed a win for the contract if they bid at their
lowest bid price of $ 7,500 and this requires that the new production process lowers the unit
production costs for each computer to $ 5,000, in which case ABC will make a profit and should
therefore bid for the project. The probability of this happening is only 0.25 while the probability of
winning the contract is theoretically 0.5. because there is a dependency on winning the tender ion
the probability of the new production costs dropping to $ 5,000 per unit, we determine the effective
probability of winning the tender by multiplying the two probabilities;
Probability for winning = 0.5 x 0.25 = 0.0125
if Complex bids at $
8,000- $ 1 million loss
8,500 850,000,000 May fail to win if
Complex bids at $
8,000 - $ 1 million loss
7,500 450, 000,000 Will definitely win
tender-BID decision
Bid using new technology
Bid prices Production costs Possible outcomes Inference
7,500 0.25 $ 5000 Can bid at 7,500 if
Complex submits its
lowest bid of $ 8,000
Will make profit, Bid
0.50 $ 7500 Will win bid $ 7,500 if
Complex submits its
lowest bid of $ 8,000
No Profit , No need to
bid
0.25 at $ 8,500 Will not win if
Complex bids at $
8,000
No Profit , No need to
bid
Final Decision and Discussion
ABC, using the new technology, can only be guaranteed a win for the contract if they bid at their
lowest bid price of $ 7,500 and this requires that the new production process lowers the unit
production costs for each computer to $ 5,000, in which case ABC will make a profit and should
therefore bid for the project. The probability of this happening is only 0.25 while the probability of
winning the contract is theoretically 0.5. because there is a dependency on winning the tender ion
the probability of the new production costs dropping to $ 5,000 per unit, we determine the effective
probability of winning the tender by multiplying the two probabilities;
Probability for winning = 0.5 x 0.25 = 0.0125
Secure Best Marks with AI Grader
Need help grading? Try our AI Grader for instant feedback on your assignments.

Effectively, this means the chance of a guaranteed win for the contract is only 1.25% which is too
risky. The decision therefore, is that ABC does not bid for the tender at all using the new production
method because the chances of losing out are way too high than the chances of winning, given the
dependencies obtaining from the set of circumstances.
Bayes Rule problem
There are two possible outcomes if an athlete is tested for drugs or any other banned substances;
they can either be positive or negative, meaning probabilities of 0.5 for either outcomes. However,
the tests are not 100% accurate; it is possible that drug free athletes will test positive while others
using drugs will test negative. It is assumed 5% of athletes use drugs with 3% of tests of athletes
that DO NOT use drugs yielding a false positive is 3%. for drug users, there is a 7% chance of
yielding a false negative from the tests results. A randomly chosen athlete is represented by D and
ND with T+ indicating a positive while T- indicating a negative test result. This problem can be
tackled using the Bayes rule;
Let T+ be the event that a drug test is positive
let T- be the event that the drug test is negative
D the event that the tested person uses the drug they have been found positive for
We seek to find P[D/T+], P[T+/ND] (false positive) and P[T-/D] (the false negative) (Soni, 2018)
We are aware that P[D] = 0.5 , P[T+] = 0.3 while P[T-] = 0.7 from this, we also know that
P[T+/ND] = 0.7 and from this, the Bayes theorem can be applied.
P[D/T+]= P[T+/ND] P[D] /P[T+]
So P[D/T+] = P[T+/D] P[D]/ P[T+/D] P[D/ND] P[ND]
Substituting, we obtain
P[D/T+] = .3 x (.5)/.3 (.5) + .5 (.7)
The probability of the a drug user being tested positive is therefore 0.98
The probability of a false positive = P[T+/ND] = 1-P[T-/ND] = 0.7
And the probability of a false negative is 1-0.98 = 0.02
risky. The decision therefore, is that ABC does not bid for the tender at all using the new production
method because the chances of losing out are way too high than the chances of winning, given the
dependencies obtaining from the set of circumstances.
Bayes Rule problem
There are two possible outcomes if an athlete is tested for drugs or any other banned substances;
they can either be positive or negative, meaning probabilities of 0.5 for either outcomes. However,
the tests are not 100% accurate; it is possible that drug free athletes will test positive while others
using drugs will test negative. It is assumed 5% of athletes use drugs with 3% of tests of athletes
that DO NOT use drugs yielding a false positive is 3%. for drug users, there is a 7% chance of
yielding a false negative from the tests results. A randomly chosen athlete is represented by D and
ND with T+ indicating a positive while T- indicating a negative test result. This problem can be
tackled using the Bayes rule;
Let T+ be the event that a drug test is positive
let T- be the event that the drug test is negative
D the event that the tested person uses the drug they have been found positive for
We seek to find P[D/T+], P[T+/ND] (false positive) and P[T-/D] (the false negative) (Soni, 2018)
We are aware that P[D] = 0.5 , P[T+] = 0.3 while P[T-] = 0.7 from this, we also know that
P[T+/ND] = 0.7 and from this, the Bayes theorem can be applied.
P[D/T+]= P[T+/ND] P[D] /P[T+]
So P[D/T+] = P[T+/D] P[D]/ P[T+/D] P[D/ND] P[ND]
Substituting, we obtain
P[D/T+] = .3 x (.5)/.3 (.5) + .5 (.7)
The probability of the a drug user being tested positive is therefore 0.98
The probability of a false positive = P[T+/ND] = 1-P[T-/ND] = 0.7
And the probability of a false negative is 1-0.98 = 0.02

Bayes Rule two outcomes and discussion
From the calculations, we see that the probability of a drug user being tested positive is 0.98 or 98%
while the probability of a non drug user being tested positive is also high at 0.7 or 70% while the
probability of a false negative where a drug user tests negative is small at 0.02 or 2%. the test can
therefore be said to be accurate only in testing positive for drug users but it is unreliable since the
probability of a non drug user testing positive is also high at 70%. therefore, we can not say for
certain that a positive result means the person is a drug user.
From the calculations, we see that the probability of a drug user being tested positive is 0.98 or 98%
while the probability of a non drug user being tested positive is also high at 0.7 or 70% while the
probability of a false negative where a drug user tests negative is small at 0.02 or 2%. the test can
therefore be said to be accurate only in testing positive for drug users but it is unreliable since the
probability of a non drug user testing positive is also high at 70%. therefore, we can not say for
certain that a positive result means the person is a drug user.

Question 2
Company Objective
The Pigskin company makes footballs and must decide the number of footballs to make every
month and has decided to use a 6 month planning horizon. Fore-casted demand for next 6 moths are
10000, 15000, 30000, 35000, 25000 and 10000. The company wants to meet the demand on time
knowing that at present it has 5000 balls in its inventory and that a months’ production can meet
demand for that month. Every month there is enough capacity to make up to 30000 footballs and the
storage capacity is for up to 10000 balls at end of month after demand occurs. Fore-casted costs of
producing the balls for next six months are $ 12.5, $ 12.55, $ 12.7, $ 12.8, $ 12.85, and $ 12.95.
Inventory holding cost for every ball at end month is at 5% of that months’ production cost. Selling
price is relevant to production decisions; Pigskin, therefore, wants to determine a production
schedule that minimizes total holding and production costs.
Changes to spreadsheet with demand
Let the production quantities be the variables P1 to P6
Let I1 to I6 be corresponding end month inventories after demand occur such that
Pj 300 and Ij 100 for every month j, I j 6
The constraints relating to P’s and I’s also need balancing
If fore-casted demand for month j is Di, then the equation for the month j is Ij-1 + Pj = Dj + Ij
Production constraints are on inventory capacity and production
These were computed in a spreadsheet and Solver used for solving various parameters and
conditions
Changes to spreadsheet with demand in any of the first 5 months, change in the optimal production
schedule and optimal total cost and discussion
Company Objective
The Pigskin company makes footballs and must decide the number of footballs to make every
month and has decided to use a 6 month planning horizon. Fore-casted demand for next 6 moths are
10000, 15000, 30000, 35000, 25000 and 10000. The company wants to meet the demand on time
knowing that at present it has 5000 balls in its inventory and that a months’ production can meet
demand for that month. Every month there is enough capacity to make up to 30000 footballs and the
storage capacity is for up to 10000 balls at end of month after demand occurs. Fore-casted costs of
producing the balls for next six months are $ 12.5, $ 12.55, $ 12.7, $ 12.8, $ 12.85, and $ 12.95.
Inventory holding cost for every ball at end month is at 5% of that months’ production cost. Selling
price is relevant to production decisions; Pigskin, therefore, wants to determine a production
schedule that minimizes total holding and production costs.
Changes to spreadsheet with demand
Let the production quantities be the variables P1 to P6
Let I1 to I6 be corresponding end month inventories after demand occur such that
Pj 300 and Ij 100 for every month j, I j 6
The constraints relating to P’s and I’s also need balancing
If fore-casted demand for month j is Di, then the equation for the month j is Ij-1 + Pj = Dj + Ij
Production constraints are on inventory capacity and production
These were computed in a spreadsheet and Solver used for solving various parameters and
conditions
Changes to spreadsheet with demand in any of the first 5 months, change in the optimal production
schedule and optimal total cost and discussion
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

In the first month, the company produced just enough balls to meet demand, in the second month,
5000 more should be produced, in the third month production should just be enough to met demand
as there is 5000 balls excess from second month. The excess 5000 should be used in month four
along with a production of 30000 to meet demand. The fifth and sixth months should see enough
production just to meet the demand.
Total production costs are $ 1,535, 563.00 and this is the perfect solution that minimizes production
and inventory costs.
70% of the production in a given month and 30% occurs too late in that month, changes in the
optimal production schedule and optimal total cost and discussion
Using Solver, balls should be produced in the month they are needed whenever possible but the
exception is the 20000 units produced in Month 2 since the demand is just for 15000. The extra
produced in month 2 are used to meet month 3 demand which is 35000 balls since all production
capacity is used to meet the demand for month 3. Month 4 exceeds production capacity so the extra
5000 balls in month 2 are used to meet total month 4 demand.
Sensitivity analysis from Solver is shown below;
A drop in holding costs to say 1% of production costs results in capacity limits being reached but if
it goes up to 10% the maximum capacity that can be held is 5000. using the six month planning
horizon, does the production towards the end of the six month planning horizon have an effect on
the first month production quantity? A solver analysis shows production quantity in the first month
remains fairly insensitive to the last months 5 and 6.
5000 more should be produced, in the third month production should just be enough to met demand
as there is 5000 balls excess from second month. The excess 5000 should be used in month four
along with a production of 30000 to meet demand. The fifth and sixth months should see enough
production just to meet the demand.
Total production costs are $ 1,535, 563.00 and this is the perfect solution that minimizes production
and inventory costs.
70% of the production in a given month and 30% occurs too late in that month, changes in the
optimal production schedule and optimal total cost and discussion
Using Solver, balls should be produced in the month they are needed whenever possible but the
exception is the 20000 units produced in Month 2 since the demand is just for 15000. The extra
produced in month 2 are used to meet month 3 demand which is 35000 balls since all production
capacity is used to meet the demand for month 3. Month 4 exceeds production capacity so the extra
5000 balls in month 2 are used to meet total month 4 demand.
Sensitivity analysis from Solver is shown below;
A drop in holding costs to say 1% of production costs results in capacity limits being reached but if
it goes up to 10% the maximum capacity that can be held is 5000. using the six month planning
horizon, does the production towards the end of the six month planning horizon have an effect on
the first month production quantity? A solver analysis shows production quantity in the first month
remains fairly insensitive to the last months 5 and 6.
Question 3
Problem statement
GulfGulf is a small company making family run firm in the UAE making golfing equipment aimed
at meeting increased demand for tourists coming for golfing holidays. It has decided to make two
new products; a medium priced golf bag and an upmarket expensive golf bag; products are priced in
$. The distributors have agreed to buy all golf bags produced in next three months. Based on the
production times and available hours, how many of the two types of gold bags should be produced
to maximize profit?
Discussion data, constraints type and objectives
The constraints here are bottlenecks in production because each activity takes different times to
complete, so there will be down time when some activities wait for completion of the predecessor
activities. The objective is to determine the best production rates for each product that results in
maximum profits. The strategy would be to produce more of the product with the highest profit, but
this is constrained by the time variances for each production activity for every product.
Analytical equations with condition forms
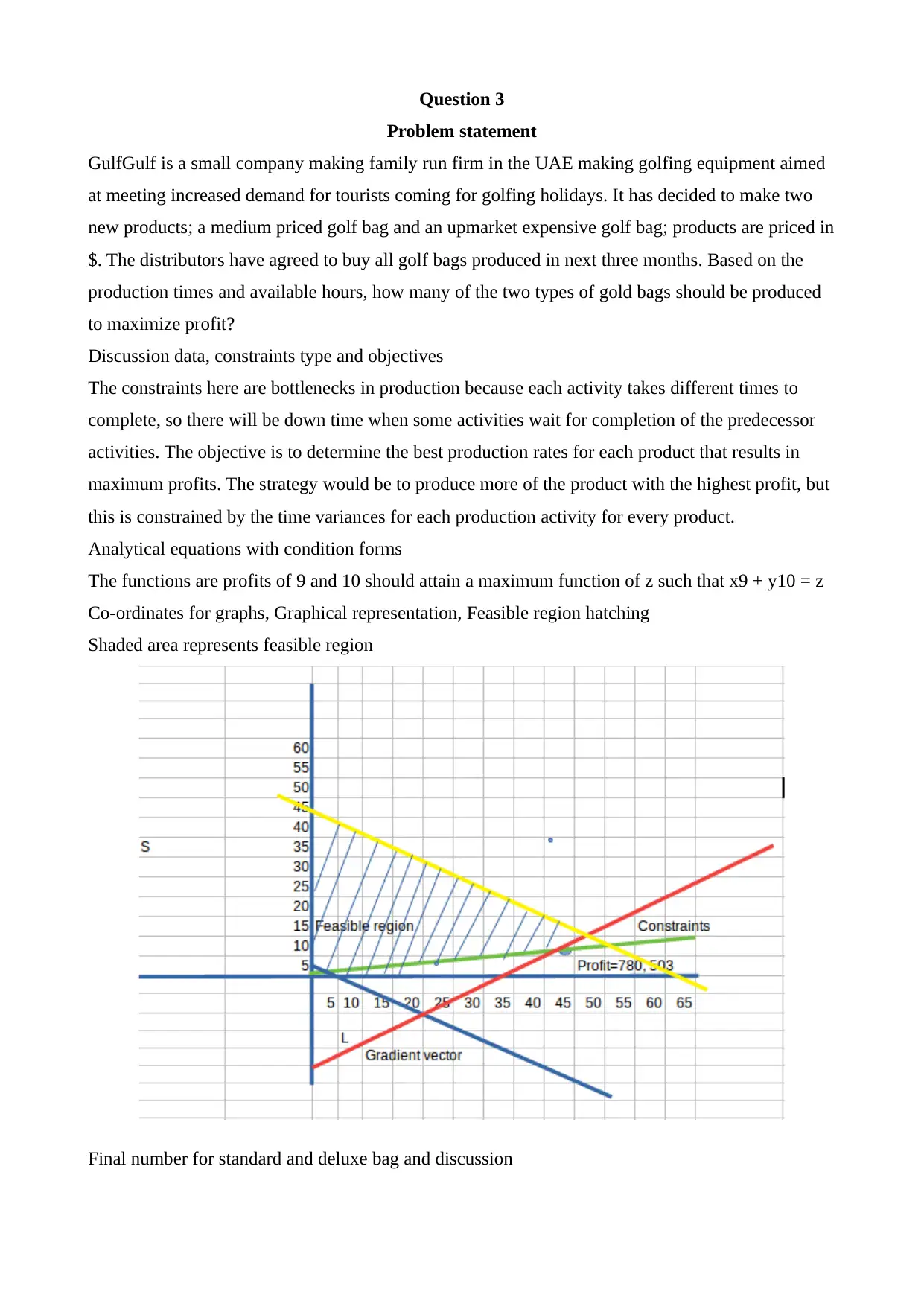
The functions are profits of 9 and 10 should attain a maximum function of z such that x9 + y10 = z
Co-ordinates for graphs, Graphical representation, Feasible region hatching
Shaded area represents feasible region
Final number for standard and deluxe bag and discussion
Problem statement
GulfGulf is a small company making family run firm in the UAE making golfing equipment aimed
at meeting increased demand for tourists coming for golfing holidays. It has decided to make two
new products; a medium priced golf bag and an upmarket expensive golf bag; products are priced in
$. The distributors have agreed to buy all golf bags produced in next three months. Based on the
production times and available hours, how many of the two types of gold bags should be produced
to maximize profit?
Discussion data, constraints type and objectives
The constraints here are bottlenecks in production because each activity takes different times to
complete, so there will be down time when some activities wait for completion of the predecessor
activities. The objective is to determine the best production rates for each product that results in
maximum profits. The strategy would be to produce more of the product with the highest profit, but
this is constrained by the time variances for each production activity for every product.
Analytical equations with condition forms
The functions are profits of 9 and 10 should attain a maximum function of z such that x9 + y10 = z
Co-ordinates for graphs, Graphical representation, Feasible region hatching
Shaded area represents feasible region
Final number for standard and deluxe bag and discussion

The company will make maximum profit by producing 780 of the standard bags and 502 of the high
end golf bags per month; over the three month period, the company should produce 2340 of the
standard bags and 1503 of the high end golf bags. Substituting in the equation, the two conditions
give a profit of $12,050 ; reducing either number results in lower profits than $12,050 per month.
end golf bags per month; over the three month period, the company should produce 2340 of the
standard bags and 1503 of the high end golf bags. Substituting in the equation, the two conditions
give a profit of $12,050 ; reducing either number results in lower profits than $12,050 per month.
Secure Best Marks with AI Grader
Need help grading? Try our AI Grader for instant feedback on your assignments.
Question 4
Simple Excel model with description
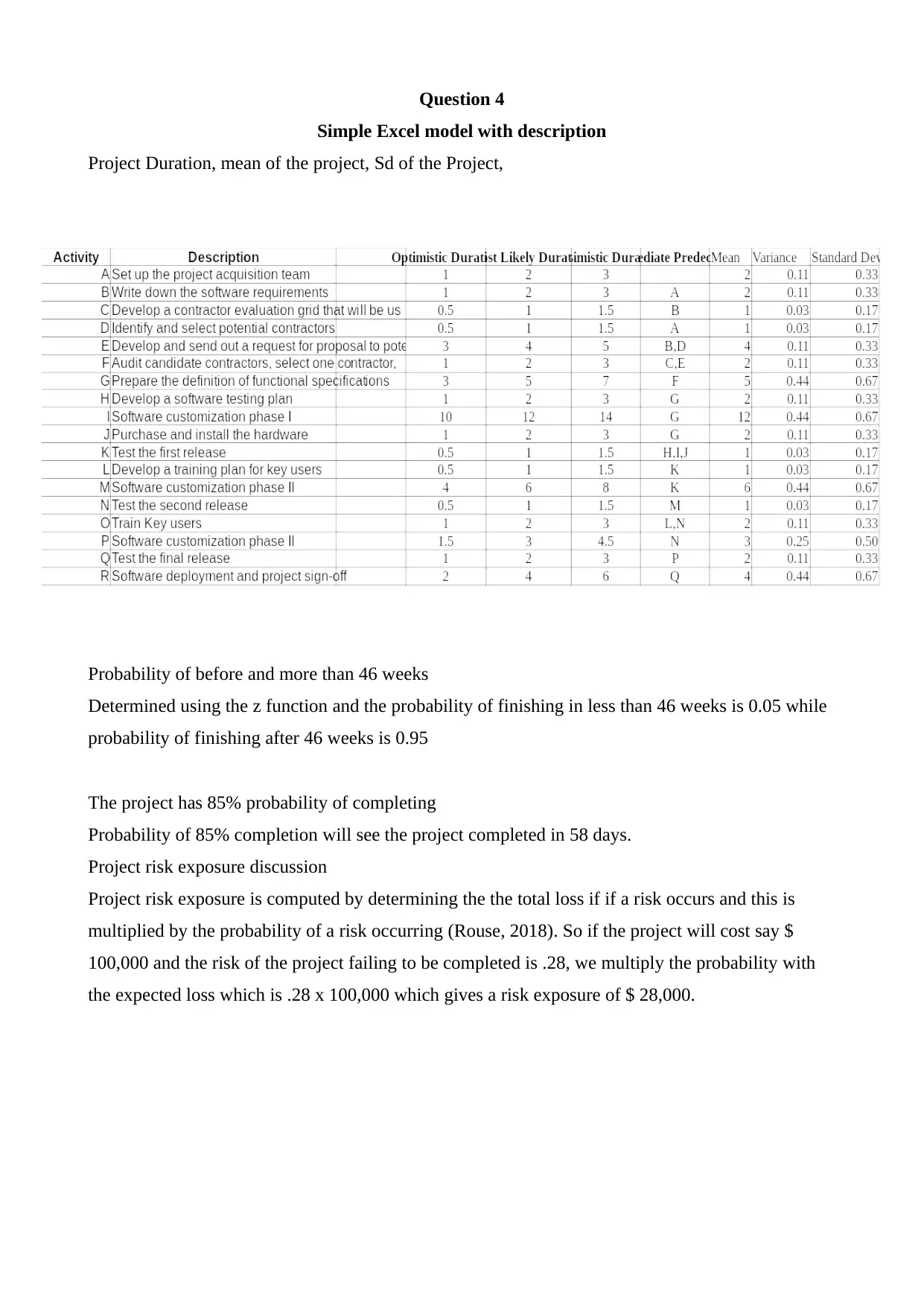
Project Duration, mean of the project, Sd of the Project,
Probability of before and more than 46 weeks
Determined using the z function and the probability of finishing in less than 46 weeks is 0.05 while
probability of finishing after 46 weeks is 0.95
The project has 85% probability of completing
Probability of 85% completion will see the project completed in 58 days.
Project risk exposure discussion
Project risk exposure is computed by determining the the total loss if if a risk occurs and this is
multiplied by the probability of a risk occurring (Rouse, 2018). So if the project will cost say $
100,000 and the risk of the project failing to be completed is .28, we multiply the probability with
the expected loss which is .28 x 100,000 which gives a risk exposure of $ 28,000.
Simple Excel model with description
Project Duration, mean of the project, Sd of the Project,
Probability of before and more than 46 weeks
Determined using the z function and the probability of finishing in less than 46 weeks is 0.05 while
probability of finishing after 46 weeks is 0.95
The project has 85% probability of completing
Probability of 85% completion will see the project completed in 58 days.
Project risk exposure discussion
Project risk exposure is computed by determining the the total loss if if a risk occurs and this is
multiplied by the probability of a risk occurring (Rouse, 2018). So if the project will cost say $
100,000 and the risk of the project failing to be completed is .28, we multiply the probability with
the expected loss which is .28 x 100,000 which gives a risk exposure of $ 28,000.
1 out of 11
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
© 2024 | Zucol Services PVT LTD | All rights reserved.

