Analysis of Rubber Band Mechanical Properties: Stiffness & Modulus

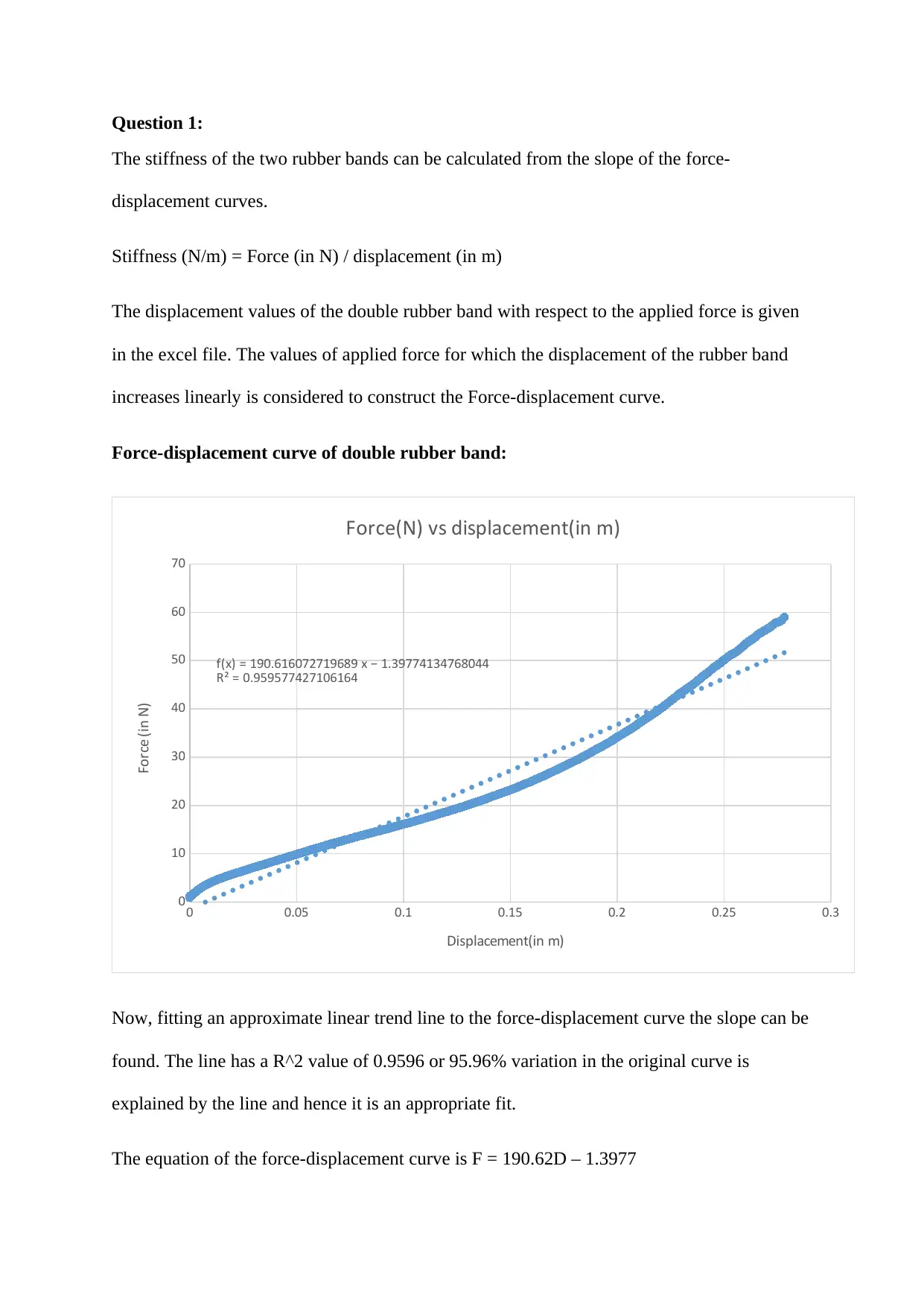
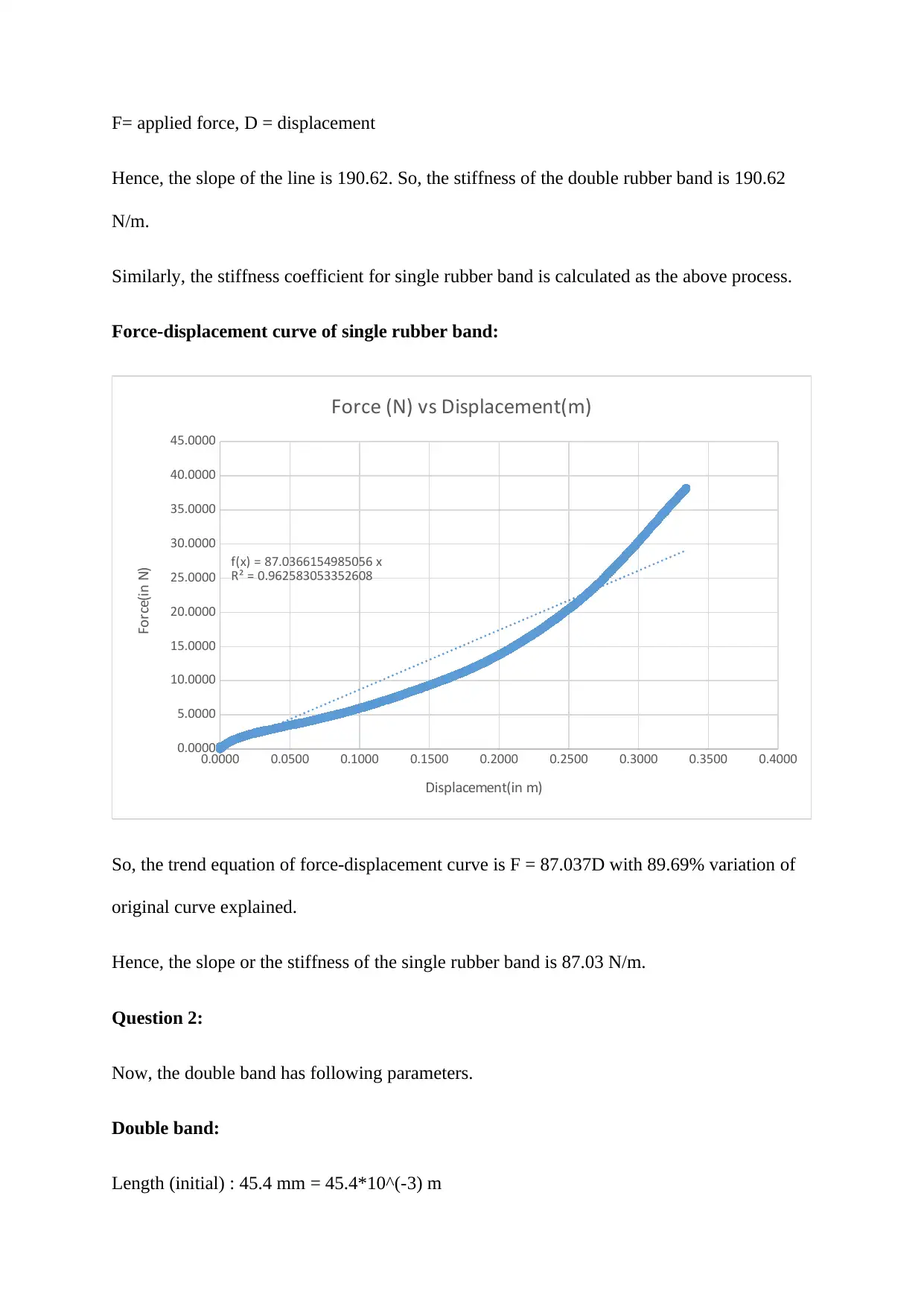
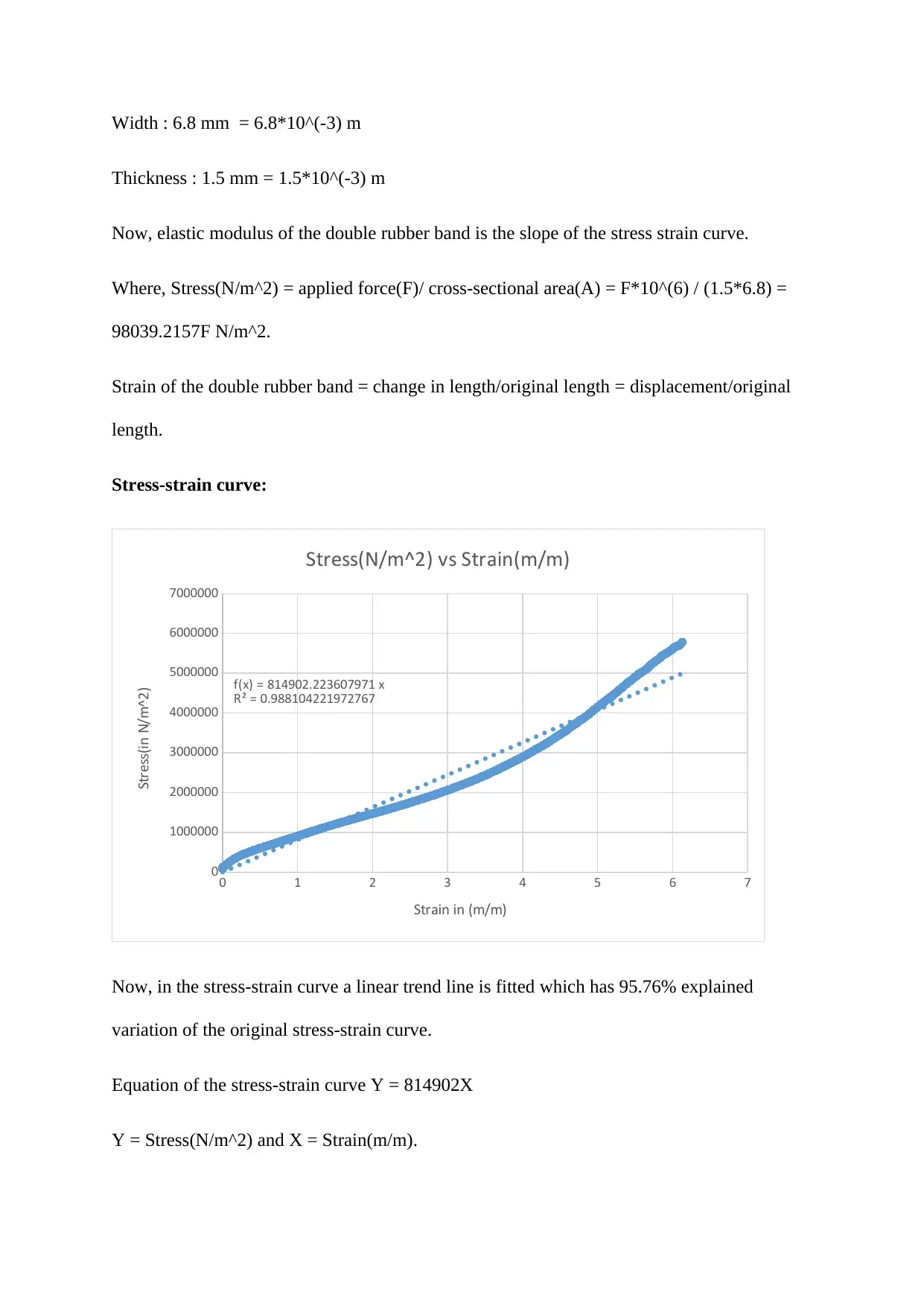
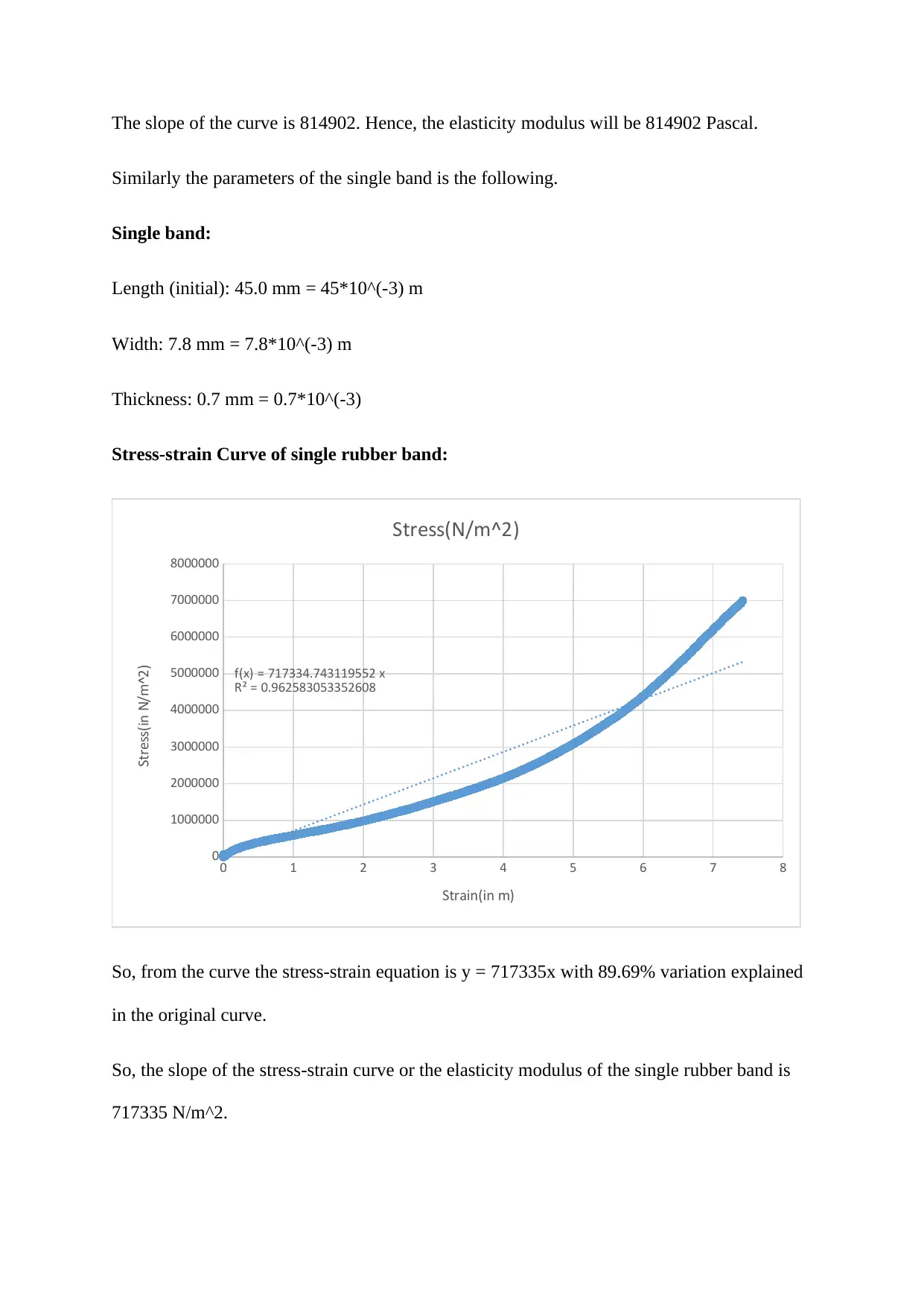
This assignment analyzes the mechanical properties of rubber bands, specifically focusing on the calculation of stiffness and elastic modulus. The solution begins by determining the stiffness of single and double rubber bands using force-displacement curves. The stiffness is calculated from the slope of the linear portion of the curves. Subsequently, the elastic modulus of both rubber band configurations is calculated using stress-strain curves. The stress-strain curves are constructed using the applied force, cross-sectional area, original length, and displacement data. The elastic modulus is then derived from the slope of the linear trend line fitted to the stress-strain curve for each rubber band configuration. The document provides detailed calculations, equations, and R-squared values for the trend lines, demonstrating a clear understanding of the underlying principles of material mechanics.

Question 1:
The stiffness of the two rubber bands can be calculated from the slope of the force-
displacement curves.
Stiffness (N/m) = Force (in N) / displacement (in m)
The displacement values of the double rubber band with respect to the applied force is given
in the excel file. The values of applied force for which the displacement of the rubber band
increases linearly is considered to construct the Force-displacement curve.
Force-displacement curve of double rubber band:
0 0.05 0.1 0.15 0.2 0.25 0.3
0
10
20
30
40
50
60
70
f(x) = 190.616072719689 x − 1.39774134768044
R² = 0.959577427106164
Force(N) vs displacement(in m)
Displacement(in m)
Force (in N)
Now, fitting an approximate linear trend line to the force-displacement curve the slope can be
found. The line has a R^2 value of 0.9596 or 95.96% variation in the original curve is
explained by the line and hence it is an appropriate fit.
The equation of the force-displacement curve is F = 190.62D – 1.3977

F= applied force, D = displacement
Hence, the slope of the line is 190.62. So, the stiffness of the double rubber band is 190.62
N/m.
Similarly, the stiffness coefficient for single rubber band is calculated as the above process.
Force-displacement curve of single rubber band:
0.0000 0.0500 0.1000 0.1500 0.2000 0.2500 0.3000 0.3500 0.4000
0.0000
5.0000
10.0000
15.0000
20.0000
25.0000
30.0000
35.0000
40.0000
45.0000
f(x) = 87.0366154985056 x
R² = 0.962583053352608
Force (N) vs Displacement(m)
Displacement(in m)
Force(in N)
So, the trend equation of force-displacement curve is F = 87.037D with 89.69% variation of
original curve explained.
Hence, the slope or the stiffness of the single rubber band is 87.03 N/m.
Question 2:
Now, the double band has following parameters.
Double band:
Length (initial) : 45.4 mm = 45.4*10^(-3) m

Width : 6.8 mm = 6.8*10^(-3) m
Thickness : 1.5 mm = 1.5*10^(-3) m
Now, elastic modulus of the double rubber band is the slope of the stress strain curve.
Where, Stress(N/m^2) = applied force(F)/ cross-sectional area(A) = F*10^(6) / (1.5*6.8) =
98039.2157F N/m^2.
Strain of the double rubber band = change in length/original length = displacement/original
length.
Stress-strain curve:
0 1 2 3 4 5 6 7
0
1000000
2000000
3000000
4000000
5000000
6000000
7000000
f(x) = 814902.223607971 x
R² = 0.988104221972767
Stress(N/m^2) vs Strain(m/m)
Strain in (m/m)
Stress(in N/m^2)
Now, in the stress-strain curve a linear trend line is fitted which has 95.76% explained
variation of the original stress-strain curve.
Equation of the stress-strain curve Y = 814902X
Y = Stress(N/m^2) and X = Strain(m/m).

The slope of the curve is 814902. Hence, the elasticity modulus will be 814902 Pascal.
Similarly the parameters of the single band is the following.
Single band:
Length (initial): 45.0 mm = 45*10^(-3) m
Width: 7.8 mm = 7.8*10^(-3) m
Thickness: 0.7 mm = 0.7*10^(-3)
Stress-strain Curve of single rubber band:
0 1 2 3 4 5 6 7 8
0
1000000
2000000
3000000
4000000
5000000
6000000
7000000
8000000
f(x) = 717334.743119552 x
R² = 0.962583053352608
Stress(N/m^2)
Strain(in m)
Stress(in N/m^2)
So, from the curve the stress-strain equation is y = 717335x with 89.69% variation explained
in the original curve.
So, the slope of the stress-strain curve or the elasticity modulus of the single rubber band is
717335 N/m^2.