Evaluating the Effectiveness of Drugs

The provided content discusses various statistical concepts, including null and alternate hypotheses, type I and II errors, and z-tests. The first part of the assignment explores the concept of alternate hypothesis, where it is discussed that both Type I and Type II errors can be severe, depending on the context. The second part of the assignment involves a series of questions related to statistical tests, including calculating test statistics (z), determining p-values, and rejecting or failing to reject null hypotheses. The specific topics covered include: actual effectiveness of drugs, z-tests for population means, and testing whether Tutor-O-Rama's services raise SAT math scores at least 50 points.

Sampling, Hypothesis Testing, and Regression
Question 1
Simple Random Sampling
A simple random sample is a subset of a statistical population in which each member of the
subset has an equal probability of being chosen. An example of a simple random sample would
be the names of 10 employees being chosen using a lottery method from a company of 100
employees. In this case, the population is 100 employees, and the sample is random because each
employee has an equal chance of being chosen.
Advantages:
1. The method is simple to use.
2. This method is an unbiased representation of a group.
3. This is suitable for data analysis which includes the use of inferential statistics.
Disadvantages:
1. A sampling error can occur with a simple random sample if the sample does not end up
accurately reflecting the population it is supposed to represent. For example, in our
simple random sample of 10 employees, it would be possible to draw 10 men even if the
population consisted of 50 women and 50 men.
2. It cannot be employed where the units of population are heterogeneous in nature.
3. This method lacks the use of available knowledge concerning the population.
Question 2
This is a case of Simple Random Sampling because the names are drawn at random and has an
equal probability of being selected.
Question 3
Yes, this sampling plan results in a random sample.
The type of sample is Systematic Random Sampling.
This sample is systematic random sampling as it does not involve separate random selection of
each household and is used to select large samples from a long list of households.

Question 4
This is neither a random nor a simple random sample. The manager only was able to talk to the
employees who were present at the meeting so those who attended the meeting never had a
chance to be chosen. These employees were not selected at random from the population of all
employees in the company. In order to have a random sample, the manager would have to
identify all employees in the company, and then randomly select a subset of them to interview.
Question 5
Yes, this sampling plan results in a random sample.
The type of sample is Cluster Random Sampling.
We can divide population into clusters (usually along geographic boundaries) then randomly
sample clusters and measure all units within sampled clusters. In this case that would consist of
randomly selecting ten schools and then interviewing all of the teachers.
Question 6
This method is the Stratified Random Sampling method because the school was separated into
similar subgroups (strata) and then one-tenth of each group was sampled to ensure the population
was proportionately represented. This method ensures each group is represents the population
appropriately.
Question 7
(a)
I would choose stratified random sampling. I would divide the employees into strata by gender
or division (assuming there are only a few divisions of the company, since we have only 100
surveys to administer). I would then randomly choose individuals from each designated groups.
Stratified random sampling is preferred over simple random sampling because it produces more
accurate estimates of the population’s characteristics, as well as providing insight into any
potential differences between the strata.

(b)
The population is all employees.
The sample group is the set of individuals chosen to complete the survey.
I would try to include every employee.
(c)
Participant bias is difficult to overcome in this case. For example, workers who are dissatisfied
may be reluctant to be honest for fear of reprisal, and if the survey is optional, respondents will
tend to be the less busy employees. Design of the survey can reduce this to some extent, but it is
difficult to completely remove it.
Question 2
(a)
The survey described here is a voluntary sample, not a random sample, and therefore admits a
likelihood of bias. Simply put, the people who have a very strong opinion about the topic are
more likely to respond.
(b)
No.
This survey does not provide sufficient evidence to support (or refute) this claim.
(c)
Because the sampling procedure is biased, no conclusion can be drawn about the results.
A survey using random sampling would provide a more accurate estimate of the population, but
even so, the use of personal opinions to gauge the market is in and of itself flawed, and highly
unreliable. It would be much preferred to utilize true market data.

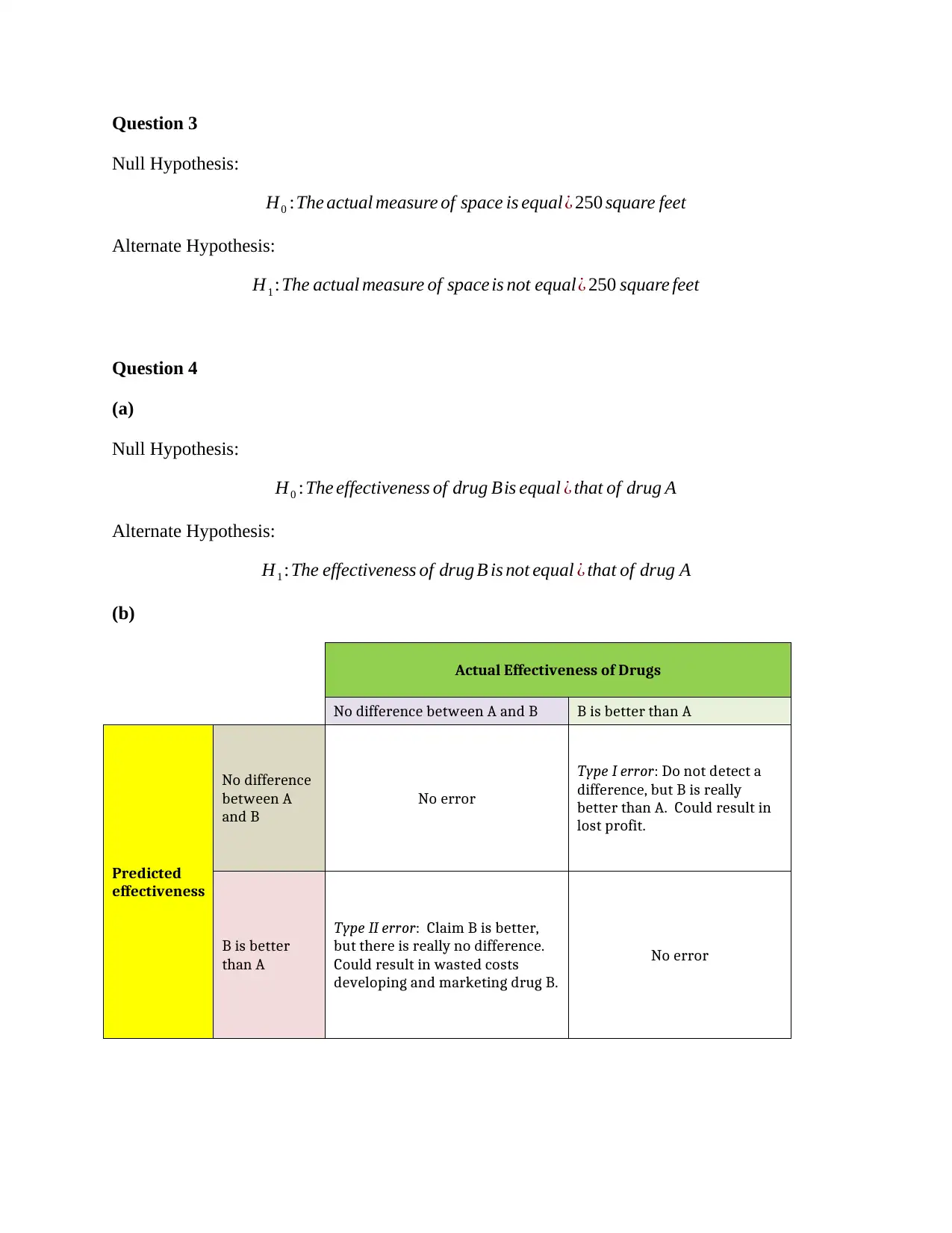
Question 3
Null Hypothesis:
H0 :The actual measure of space is equal¿ 250 square feet
Alternate Hypothesis:
H1 :The actual measure of space is not equal¿ 250 square feet
Question 4
(a)
Null Hypothesis:
H0 :The effectiveness of drug Bis equal ¿ that of drug A
Alternate Hypothesis:
H1 :The effectiveness of drug B is not equal ¿ that of drug A
(b)
Actual Effectiveness of Drugs
No difference between A and B B is better than A
Predicted
effectiveness
No difference
between A
and B
No error
Type I error: Do not detect a
difference, but B is really
better than A. Could result in
lost profit.
B is better
than A
Type II error: Claim B is better,
but there is really no difference.
Could result in wasted costs
developing and marketing drug B.
No error

(c)
Both errors can be severe.
If the drug is a very important product in the marketplace, then perhaps the Type I error is more
severe. This is because the Type I error may go forever unknown, as they abandon research on a
drug that would have been a huge profit center for the company.
On the other hand, the Type II error would likely result in more money spent readying the drug
for the market. Then its lack of increased effectiveness could well be caught in subsequent trials.
Even if not, it would probably have reasonable sales at first until its lack of effectiveness was
eventually borne out from increased statistics.
Question 5
(a)
Null Hypothesis:
H0 :The mean volume of each bottle is equal¿ 6 ounces .
Alternate Hypothesis:
H1 :The mean volume of each bottleis not equal¿ 6 ounces .
(b)
At the centre of the hypothesized distribution will be the highest possible value for which H0
could be true, μ0 = 6 ounces.
We will assume the significance level as α = 0.1.
The population standard deviation (σ) is known, so the normal distribution is appropriate and
therefore we will calculate the test statistics (ᴢ) as:
z = (x̅ - μ0) / (σ/√N)
= (5.989 – 6)/ (0.3/√10)
= -0.1158
For a two-tail z-test in which α = 0.1, z = -2.326 and z = +2.326 will be the respective boundaries
for lower and upper tails of 0.01 each. These are the critical values for the test and they identify
the non rejection and rejection regions i.e. reject H0 if calculated z < -2.326 or z > +2.326,
otherwise do not reject.

The calculated value, z = -0.1158 falls within the rejection region of the diagram. So at the 0.1
level of significance, the null hypothesis is rejected.
(c)
P-value = (-0.1158 ≤ Z ≤ 0.1158) = approximately 2*(1 – 0.546) = 0.908.
(d)
We do not reject the null hypothesis. (Although we did not specify a significance level, the P
value is very large, and no reasonable significance level would be satisfied). Therefore, we do
not have sufficient evidence to conclude that the bottles are inadequately filled.
Question 6
z = (x̅ - μ0) / σ
= (20 – 17)/ (3.4)
= 0.8824.
Question 7
Using a standard normal probabilities table,
P¿=0.1888
Ptwo−sided =0.3776
This means that:
1. The probability that a value of 20 or greater would occur by chance is 18.88%.
2. The probability that a value of 17±3 would occur by chance is 37.76%.

Question 8
z = (x̅ - μ0) / σ
= (12 – 14)/ (1.9)
= -1.0526
The probability that babysitter wage is greater than $ 12 per hour:
P ( x ≥ 12 )=1−P ( x <12 )
¿ 1−P ( z <−1.0526 )
From z - score table the probability is:
P ( z<−1.0526 )=0.1469
Therefore,
P ( x ≥ 12 ) =1−0.1469
¿ 0.8531
The probability that babysitter wage is greater than $ 12 per hour is 0.8531.
At a rate of $12/hr, she is being underpaid as compared to a typical babysitter. At this level,
there are only 14.69% of the babysitters that are paid less than she is. I would give her a raise.
Question 9
(a)
We want to see if Tutor-O-Rama’s services will raise a student’s SAT math scores at least
50points or not. The null hypothesis is that the services will not raise SAT math score more than
50 points and the alternative is it will increase by at least 50 points.
Null Hypothesis:
H0 :The mean score of tutored student is 400
Alternate Hypothesis:
H1 :The mean score of tutored student is not equal ¿ 400

This is a one sample test for mean and as the population standard deviation is known so the most
appropriate is the Z test.
z= 385−400
35
√ 100
¿−4.286
p−value=P ( z >−4.286 ) =3.67∗10−5
Since the P value is less than both of our significance level of 0.01 and 0.05, we have sufficient
evidence to reject the null hypothesis.
(b)
The p-value is less than the significance level for both 1% and 5% significance level. I will reject
the null hypothesis concluding that the average score of 385 points is significant at the 5% and
1% level. The claim that their services will raise student SAT math scores at least 50 points is
not true. We can therefore conclude that Tutor-O-Rama’s claim is false at the 95 and 99%
confidence level.