Analysis of Forest Fires Dataset using Linear Regression

The article explores the Forest Fires dataset using linear regression and analyzes the significance of predictors like temperature, relative humidity, wind and rain in determining the area affected by forest fires. It includes scatter plots, histograms, multiple regression analysis, and prediction of the area affected by forest fires based on the predictor variables.

1) I)data=(read.table("C:\\Users\\Subhojit\\Desktop\\NERDY TUTLEZ\\898908\\Forest718.txt"))
colnames(data)=c("X1","X2","month","day","FFMC","DMC","DC","ISI","temp","RH","wind","r
ain","area")
II) sampledata = data[sample(1:517,200),c(1:13)]
III) Scatter Plot
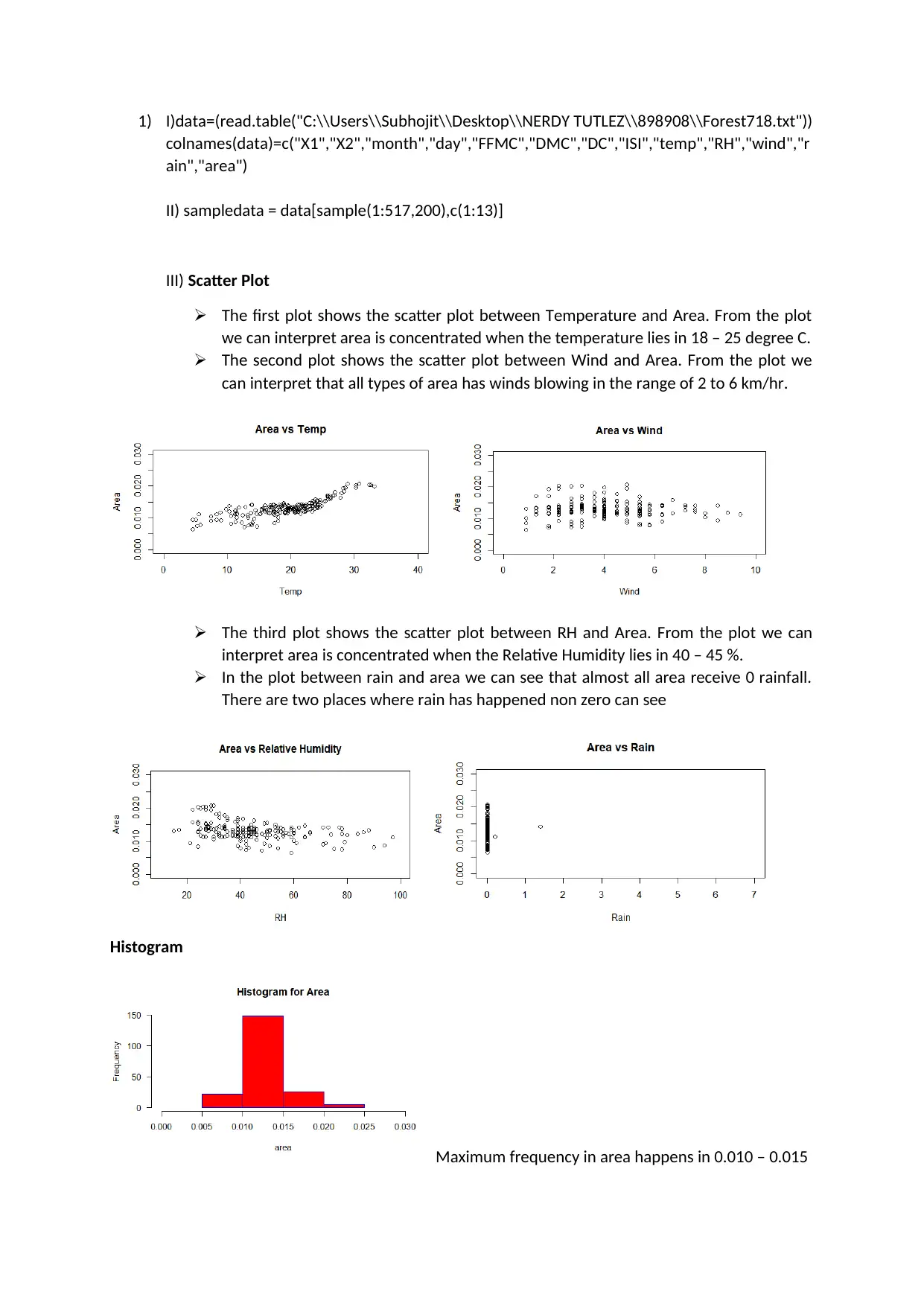
 The first plot shows the scatter plot between Temperature and Area. From the plot
we can interpret area is concentrated when the temperature lies in 18 – 25 degree C.
 The second plot shows the scatter plot between Wind and Area. From the plot we
can interpret that all types of area has winds blowing in the range of 2 to 6 km/hr.
 The third plot shows the scatter plot between RH and Area. From the plot we can
interpret area is concentrated when the Relative Humidity lies in 40 – 45 %.
 In the plot between rain and area we can see that almost all area receive 0 rainfall.
There are two places where rain has happened non zero can see
Histogram
Maximum frequency in area happens in 0.010 – 0.015

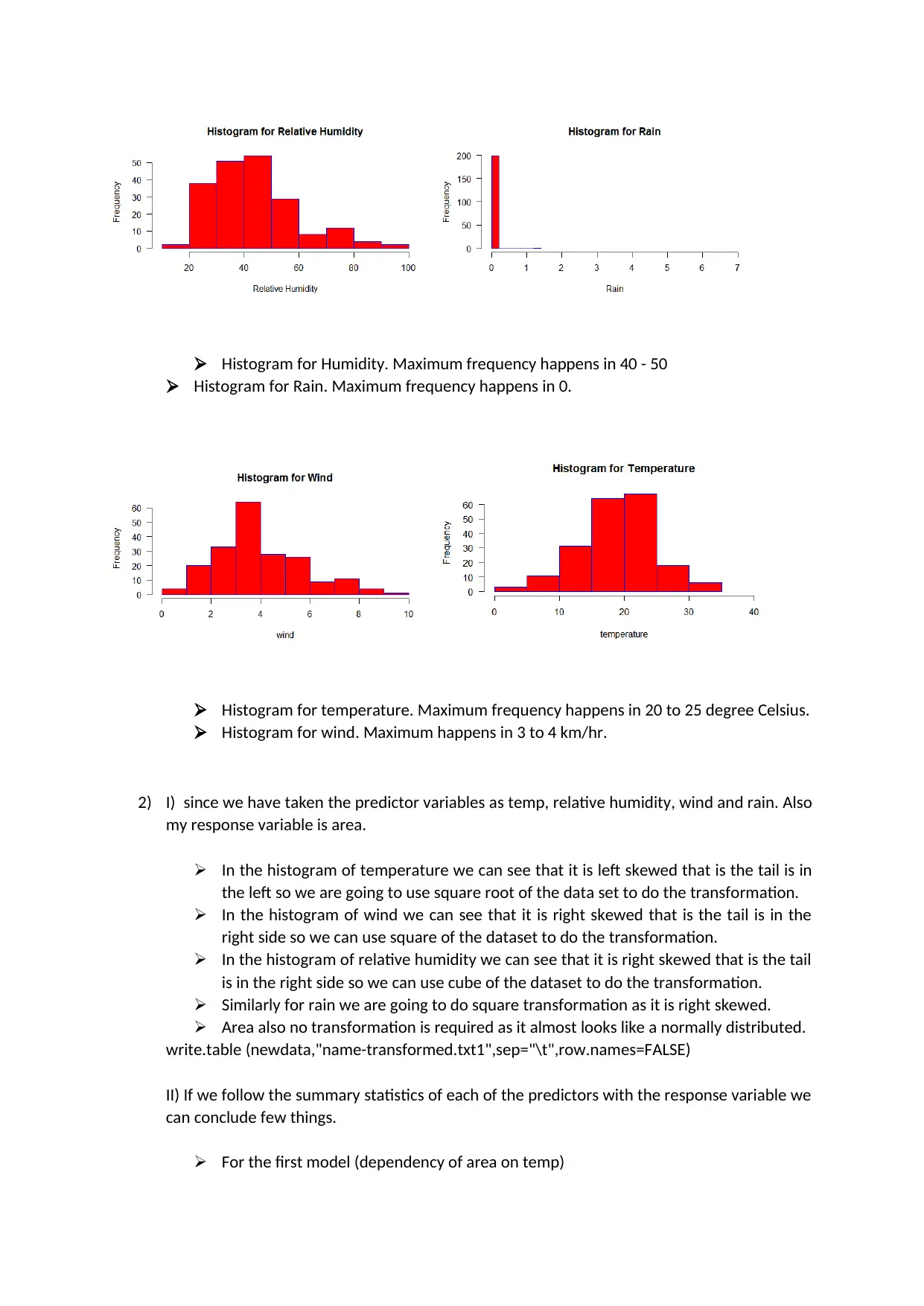
 Histogram for Humidity. Maximum frequency happens in 40 - 50
 Histogram for Rain. Maximum frequency happens in 0.
 Histogram for temperature. Maximum frequency happens in 20 to 25 degree Celsius.
 Histogram for wind. Maximum happens in 3 to 4 km/hr.
2) I) since we have taken the predictor variables as temp, relative humidity, wind and rain. Also
my response variable is area.
 In the histogram of temperature we can see that it is left skewed that is the tail is in
the left so we are going to use square root of the data set to do the transformation.
 In the histogram of wind we can see that it is right skewed that is the tail is in the
right side so we can use square of the dataset to do the transformation.
 In the histogram of relative humidity we can see that it is right skewed that is the tail
is in the right side so we can use cube of the dataset to do the transformation.
 Similarly for rain we are going to do square transformation as it is right skewed.
 Area also no transformation is required as it almost looks like a normally distributed.
write.table (newdata,"name-transformed.txt1",sep="\t",row.names=FALSE)
II) If we follow the summary statistics of each of the predictors with the response variable we
can conclude few things.
 For the first model (dependency of area on temp)

Call:
lm(formula = area ~ trans_rain, data = newdata)
Residuals:
Min 1Q Median 3Q Max
-0.0065942 -0.0016419 -0.0001456 0.0010802 0.0074255
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.0129869 0.0002050 63.337 <2e-16 ***
trans_rain 0.0007795 0.0014019 0.556 0.579
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.002886 on 198 degrees of freedom
Multiple R-squared: 0.001559, Adjusted R-squared: -0.003483
F-statistic: 0.3092 on 1 and 198 DF, p-value: 0.5788
Here from the p value we can say coefficients are insignificant so rain cannot be considered as one of
the factors for the Area
 For the second model(dependency of area on relative humidity)
Call:
lm(formula = area ~ trans_RH, data = newdata)
Residuals:
Min 1Q Median 3Q Max
-0.0062184 -0.0017496 0.0000532 0.0012283 0.0068708
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1.363e-02 2.507e-04 54.370 < 2e-16 ***
trans_RH -4.955e-09 1.224e-09 -4.047 7.43e-05 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.002776 on 198 degrees of freedom
Multiple R-squared: 0.07641, Adjusted R-squared: 0.07174
F-statistic: 16.38 on 1 and 198 DF, p-value: 7.427e-05
Here from the p value we can say coefficients are significant so relative humidity can be considered
as one of the factors for the Area
 For the third model (dependency of area on temp)
Call:
lm(formula = area ~ trans_temp, data = newdata)
Residuals:
Min 1Q Median 3Q Max
-0.0043020 -0.0012047 -0.0001768 0.0010320 0.0058853
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.0002089 0.0007004 0.298 0.766
trans_temp 0.0029998 0.0001617 18.551 <2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.001746 on 198 degrees of freedom
Multiple R-squared: 0.6348, Adjusted R-squared: 0.6329
F-statistic: 344.1 on 1 and 198 DF, p-value: < 2.2e-16
Here from the p value we can say coefficients are significant so Temperature can be considered as
one of the factors for the Area
 For the fourth model (dependency of area on wind)

Call:
lm(formula = area ~ trans_wind, data = newdata)
Residuals:
Min 1Q Median 3Q Max
-0.0070462 -0.0014876 -0.0000435 0.0013324 0.0073492
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1.346e-02 2.957e-04 45.515 <2e-16 ***
trans_wind -2.413e-05 1.131e-05 -2.133 0.0341 *
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.002856 on 198 degrees of freedom
Multiple R-squared: 0.02246, Adjusted R-squared: 0.01753
F-statistic: 4.55 on 1 and 198 DF, p-value: 0.03415
Here from the p value we can say coefficients are insignificant so wind cannot be considered as one
of the factors for the Area.
3) I) since we have four predictors now we are going to use multiple regression with the
transformed variables and we are going to check the importance of each of the predictors in
the determination of the response variable.
II)
III) We can see that out all the four predictors all the last three are significant in nature and if we
check the Adjusted R-squared for the model we can see that it is 60.2% indicates that the model fits

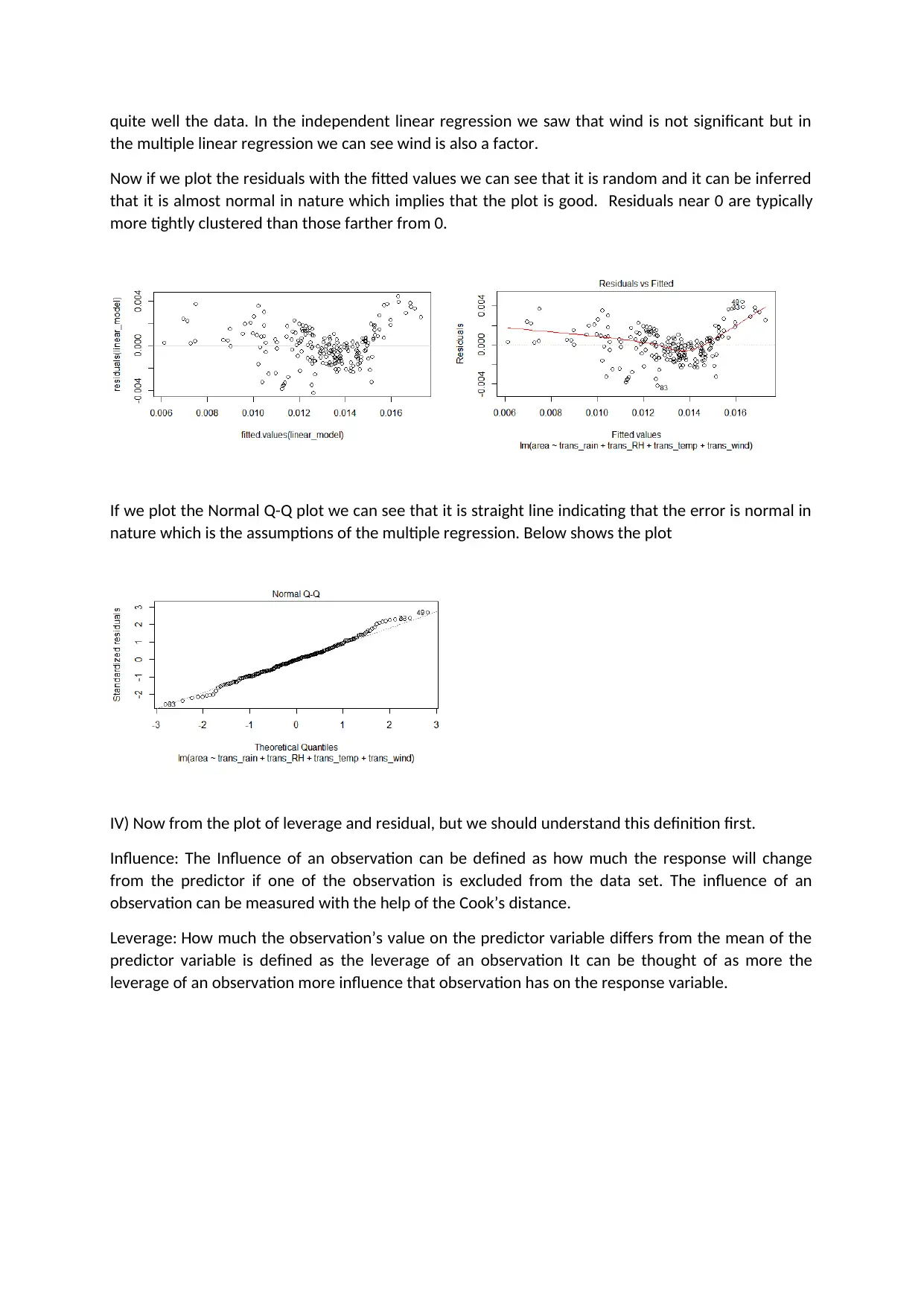
quite well the data. In the independent linear regression we saw that wind is not significant but in
the multiple linear regression we can see wind is also a factor.
Now if we plot the residuals with the fitted values we can see that it is random and it can be inferred
that it is almost normal in nature which implies that the plot is good. Residuals near 0 are typically
more tightly clustered than those farther from 0.
If we plot the Normal Q-Q plot we can see that it is straight line indicating that the error is normal in
nature which is the assumptions of the multiple regression. Below shows the plot
IV) Now from the plot of leverage and residual, but we should understand this definition first.
Influence: The Influence of an observation can be defined as how much the response will change
from the predictor if one of the observation is excluded from the data set. The influence of an
observation can be measured with the help of the Cook’s distance.
Leverage: How much the observation’s value on the predictor variable differs from the mean of the
predictor variable is defined as the leverage of an observation It can be thought of as more the
leverage of an observation more influence that observation has on the response variable.

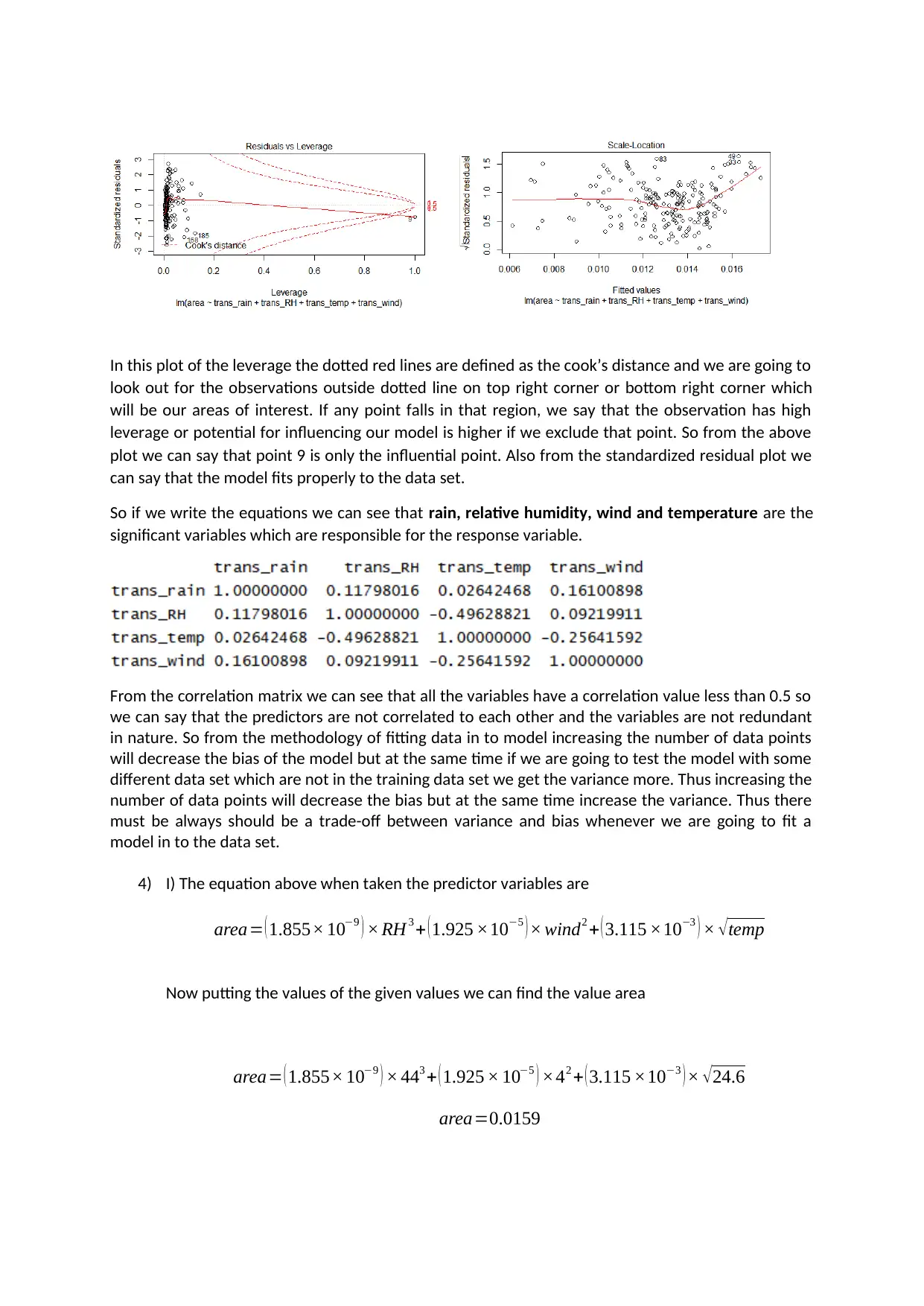
In this plot of the leverage the dotted red lines are defined as the cook’s distance and we are going to
look out for the observations outside dotted line on top right corner or bottom right corner which
will be our areas of interest. If any point falls in that region, we say that the observation has high
leverage or potential for influencing our model is higher if we exclude that point. So from the above
plot we can say that point 9 is only the influential point. Also from the standardized residual plot we
can say that the model fits properly to the data set.
So if we write the equations we can see that rain, relative humidity, wind and temperature are the
significant variables which are responsible for the response variable.
From the correlation matrix we can see that all the variables have a correlation value less than 0.5 so
we can say that the predictors are not correlated to each other and the variables are not redundant
in nature. So from the methodology of fitting data in to model increasing the number of data points
will decrease the bias of the model but at the same time if we are going to test the model with some
different data set which are not in the training data set we get the variance more. Thus increasing the
number of data points will decrease the bias but at the same time increase the variance. Thus there
must be always should be a trade-off between variance and bias whenever we are going to fit a
model in to the data set.
4) I) The equation above when taken the predictor variables are
area= ( 1.855× 10−9 ) × RH 3 + ( 1.925 ×10−5 ) × wind2 + ( 3.115 ×10−3 ) × √temp
Now putting the values of the given values we can find the value area
area= ( 1.855× 10−9 ) × 443 + ( 1.925 × 10−5 ) ×42 + ( 3.115 ×10−3 ) × √24.6
area=0.0159

II) The area we have obtained is 0.0159 which is within the range of the values so we can say
that the prediction of the area looks good. It is quite reasonable. Though it is not within the
maximum area we have found out from the histogram
III) The values which can be considered for predictions of the area from the four predictor
variables can be chosen in such a way that it lies within the range of 0.010 and 0.015.
The values that we can consider are:
1)Rain can take any value as in my model rain is not at all significant.
2)Relative Humidity: 44
3) Temp : 20
4) Wind: 4
References
Anon., 2017. UCI Machine Learning Repository: Forest Fires Data Set. Archive.ics.uci.edu. N.p..
[Online]
Available at: http://archive.ics.uci.edu/ml/datasets/Forest+Fires
[Accessed 29 Apr 2017].
Cortez, P. a. M., 2007. A data mining approach to predict forest fires using meteorological data.
[Online]
Available at: http://www3.dsi.uminho.pt/pcortez/fires.pdf
Happe, H., 2017. Meteomalaga. [Online]
Available at: https://Malagaweather.com
[Accessed 29 Apr 2017].
NA, 2017. Forest Fires Dataset". Dsi.uminho.pt. N.p.. [Online]
Available at: www.dsi.uminho.pt/~pcortez/forestfires
[Accessed 29 Apr 2017].
NA, 2017. Montesinho.Com - Nature Tourism In Montesinho Natural Park". montesinho.com. N.p..
[Online]
Available at: https://www.montesinho.com/en
[Accessed 29 Apr 2017].