Regression and Forecasting

This report explores the concepts of regression and forecasting in the context of an online education database. It covers topics such as analyzing the relationship between variables, creating scatter diagrams, assessing the fit of the regression equation, and using regression results for forecasting. The report focuses on retention and graduation rates for different colleges.

Regression and
Forecasting

Table of Contents
Table of Contents.............................................................................................................................2
INTRODUCTION...........................................................................................................................1
MAIN BODY..................................................................................................................................1
a. Using the excel tool regression to get the relationship between the two variables..................1
b. Creating a scatter diagram for the two variables and display the regression equation and R
square on the chart.......................................................................................................................3
c. Analysis of that the estimated equation is providing a good fit or not....................................4
d. Use of regression results for forecasting purpose....................................................................5
CONCLUSION................................................................................................................................6
REFERENCES................................................................................................................................7

INTRODUCTION
Regression could be defined as a statistical method which is used in studies to determine
the relationship between two different variables. Apart from this, it is also used to analyse the
character and strength of the relation of dependent and independent variables. On the other hand,
forecasting is the process of estimating the future values on the basis of the results that are
generated through regression analysis (Angarita-Zapata, Masegosa and Triguero, 2020). These
two procedures are interlinked with each other because in order to perform activities related to
forecasting it will eb very important to use the outcomes that are generated with the help of
regression. Present report is based upon the online education data base. The two variables that
are taken in it for the analysis purpose are retention and graduation rate for different colleges.
This report will cover different topics such as analysis of relationship with the help of regression,
creation of scatter diagram and assessment of the accuracy of regression equation. Additionally,
the capability of using the regression result for forecasting is also analysed under this project.
MAIN BODY
a. Using the excel tool regression to get the relationship between the two variables
Output from excel calculations:
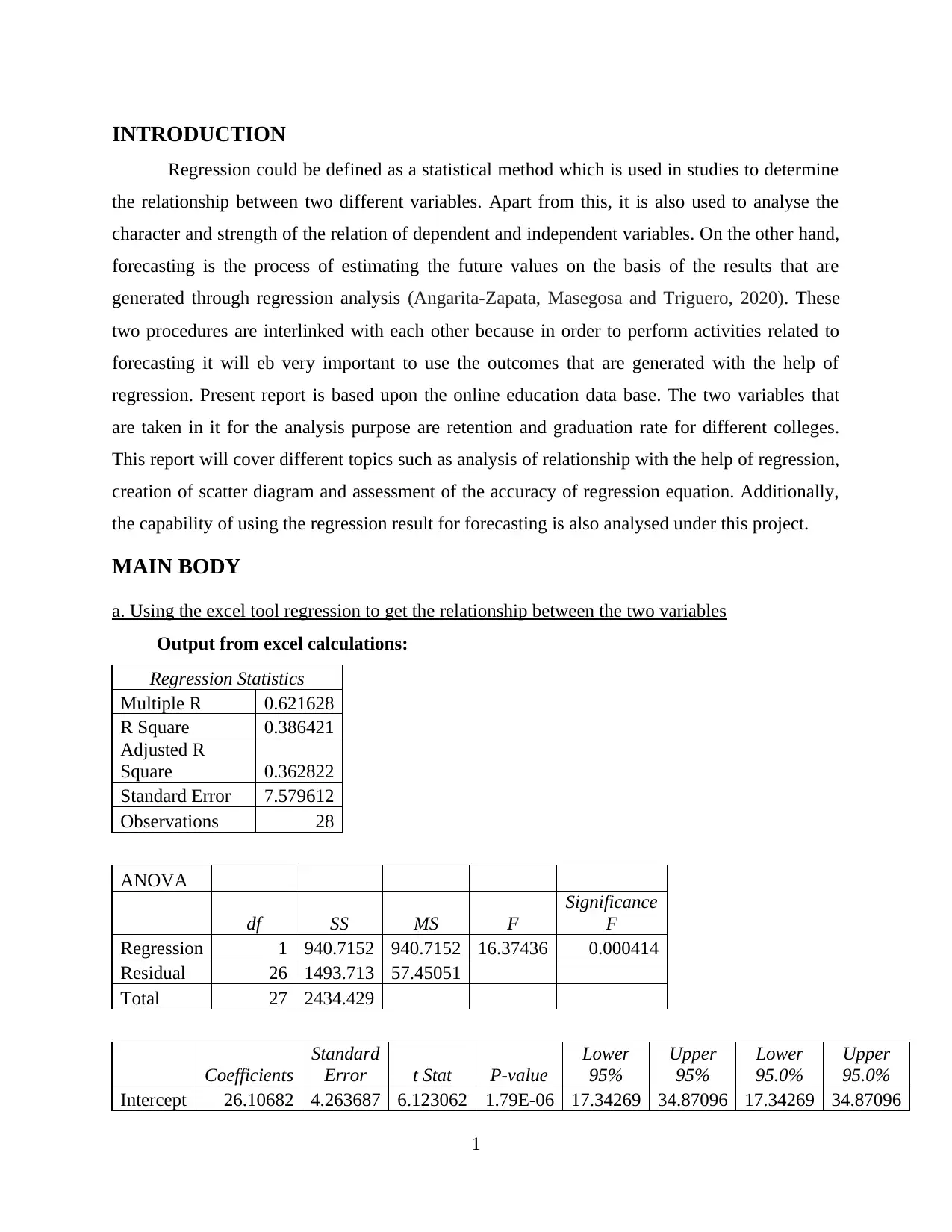
Regression Statistics
Multiple R 0.621628
R Square 0.386421
Adjusted R
Square 0.362822
Standard Error 7.579612
Observations 28
ANOVA
df SS MS F
Significance
F
Regression 1 940.7152 940.7152 16.37436 0.000414
Residual 26 1493.713 57.45051
Total 27 2434.429
Coefficients
Standard
Error t Stat P-value
Lower
95%
Upper
95%
Lower
95.0%
Upper
95.0%
Intercept 26.10682 4.263687 6.123062 1.79E-06 17.34269 34.87096 17.34269 34.87096
1

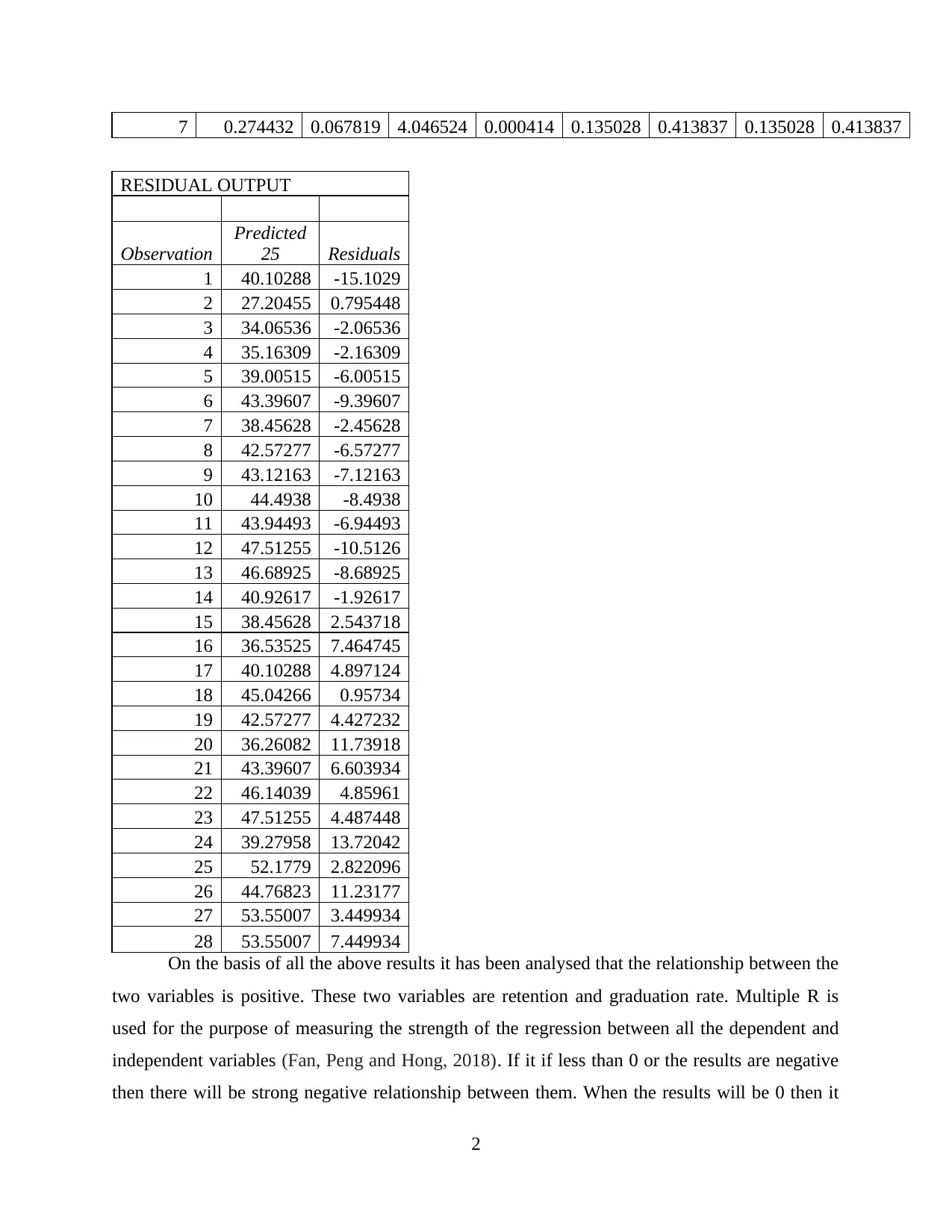
7 0.274432 0.067819 4.046524 0.000414 0.135028 0.413837 0.135028 0.413837
RESIDUAL OUTPUT
Observation
Predicted
25 Residuals
1 40.10288 -15.1029
2 27.20455 0.795448
3 34.06536 -2.06536
4 35.16309 -2.16309
5 39.00515 -6.00515
6 43.39607 -9.39607
7 38.45628 -2.45628
8 42.57277 -6.57277
9 43.12163 -7.12163
10 44.4938 -8.4938
11 43.94493 -6.94493
12 47.51255 -10.5126
13 46.68925 -8.68925
14 40.92617 -1.92617
15 38.45628 2.543718
16 36.53525 7.464745
17 40.10288 4.897124
18 45.04266 0.95734
19 42.57277 4.427232
20 36.26082 11.73918
21 43.39607 6.603934
22 46.14039 4.85961
23 47.51255 4.487448
24 39.27958 13.72042
25 52.1779 2.822096
26 44.76823 11.23177
27 53.55007 3.449934
28 53.55007 7.449934
On the basis of all the above results it has been analysed that the relationship between the
two variables is positive. These two variables are retention and graduation rate. Multiple R is
used for the purpose of measuring the strength of the regression between all the dependent and
independent variables (Fan, Peng and Hong, 2018). If it if less than 0 or the results are negative
then there will be strong negative relationship between them. When the results will be 0 then it
2

will reflect the no relationship between the variables. If the results will be more than 0 or 1 then
it will reflect the positive relationship. On the basis of it, it has been analysed that there is
positive relationship between the variables because the value of multiple R is 0.621 which is
more than 0.
R square is the coefficient of determination which is used as the indicator of goodness of
fit. With the help of it, the way in which many points fall on the regression line could be
analysed. When the value of it is 95% or more than it then it is considered a good fit. In the
results above that are generated in context of retention and graduation rate of 29 colleges the R
square is 0.386 which is not good. It shows that 38% of the values fit to the regression model. It
also shows that only 38% of the dependent variables are explained by the dependent variables.
As it the value of it is very low as compares to the ideal value which is 95% so it is not a good
fit.
Standard error is also a measure which is used for the purpose of analysing the good fit. It
is the absolute measure that reflects the average distance which is used to analysis the regression
line falls for data distance. In the above results the value of it is 7.58 which shows that the data is
not having good fit (Fleming and Goodbody, 2019).
Total observations in the above data set are 28 which are analysed for the purpose of
assessing the good it for the data as well as the interrelationship between them.
On the basis of above discussion, it has been determined that the relationship between the
variables is positive but the values are not having good fit on the basis of standard error and r
square.
b. Creating a scatter diagram for the two variables and display the regression equation and R
square on the chart
In order to reflect the regression equation and r square value on the chart following chart
is created which is as follows:
3

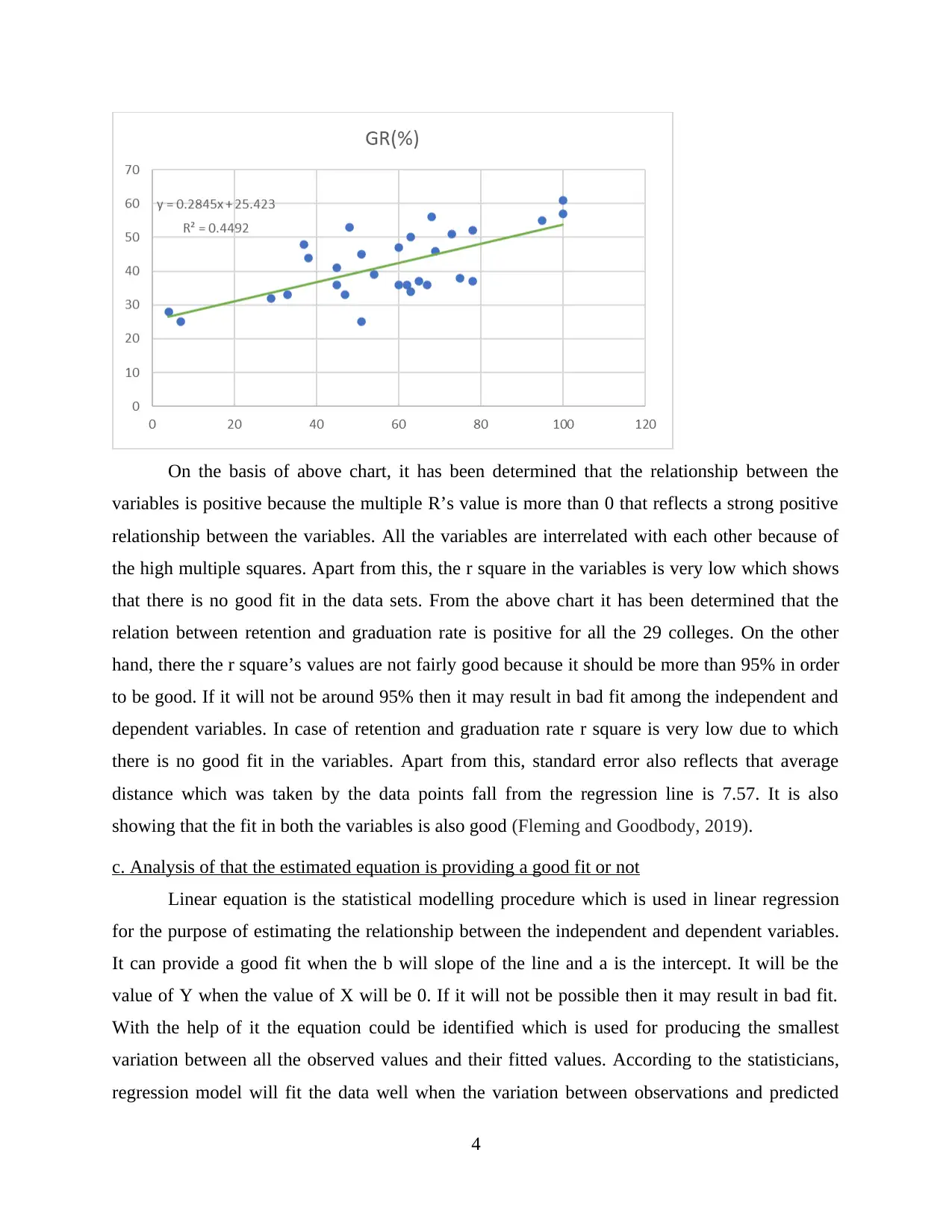
On the basis of above chart, it has been determined that the relationship between the
variables is positive because the multiple R’s value is more than 0 that reflects a strong positive
relationship between the variables. All the variables are interrelated with each other because of
the high multiple squares. Apart from this, the r square in the variables is very low which shows
that there is no good fit in the data sets. From the above chart it has been determined that the
relation between retention and graduation rate is positive for all the 29 colleges. On the other
hand, there the r square’s values are not fairly good because it should be more than 95% in order
to be good. If it will not be around 95% then it may result in bad fit among the independent and
dependent variables. In case of retention and graduation rate r square is very low due to which
there is no good fit in the variables. Apart from this, standard error also reflects that average
distance which was taken by the data points fall from the regression line is 7.57. It is also
showing that the fit in both the variables is also good (Fleming and Goodbody, 2019).
c. Analysis of that the estimated equation is providing a good fit or not
Linear equation is the statistical modelling procedure which is used in linear regression
for the purpose of estimating the relationship between the independent and dependent variables.
It can provide a good fit when the b will slope of the line and a is the intercept. It will be the
value of Y when the value of X will be 0. If it will not be possible then it may result in bad fit.
With the help of it the equation could be identified which is used for producing the smallest
variation between all the observed values and their fitted values. According to the statisticians,
regression model will fit the data well when the variation between observations and predicted
4

values are unbiased and small. With the help of regression equation, the relationship of the
outcome and predictor variables could be determined. It allows the users to predict the outcome
with a small possibility of error. While formulating the regression equation two main factors are
considered which are r square and adjusted r square (Johannesen, Kolhe and Goodwin, 2019).
With the help of r square the quality of the fit could be determined. The linear equation for the
two variables is as follows:
Y = 0.2845x + 25.423
The above calculation is not providing the good fit because of the unfavourable values of
r square and adjusted r square. Another reasons of it is the very high level of standard error. It is
mainly used for the purpose of predicting the scores of one variable from the score on the
another variable. As it does not provide the good fit so it will not be possible to use the outcomes
of it for the purpose of analysing future values. The equation is estimated and it does not provide
the good fit for the variables because of the unfavourable nature of it. When the equation results
in predicted values close to the data which is being observed then it reflects that it is resulting in
good it. As the equation is showing that the predicted values are not close to the data which is
being observed so it is not the resulting in good fit.
d. Use of regression results for forecasting purpose
If I will be working as the president of south university if I would be required to use the
results of the regression analysis for the purpose of forecasting then different aspects are required
to be analysed by me. I can use the information for forecasting purpose but only if it will provide
good fit for the data. If the results that are generated by the analysis will not provide the good fit
then it means that it is not able to provide the estimation for future and in this case, it could not
be used for forecasting purpose. While working as the president of south university it will eb
very important for me to make sure that I am able to analyse the relationship in both the
independent and dependent variables. In the case of retention and graduation rate of 29 different
colleges there is a positive relationship between the variables but the fit is not good. Due to this,
there is a high possibility of less use of the information in the forecasting procedures (Liang, Niu
and Hong, 2019).
As the president of south university, I could not use the results for forecasting future
outcomes because of the negative or unfavourable fit. The r square, adjusted r square and
standard errors are showing that the linear equation is not providing good fit. When the fit is not
5

good then it shows that data set could not be used for forecasting purpose. Hence, as the
president I would not be able to use the regression results for the purpose of forecasting. If the
data or the equation would be able to provide the good fit then it would have been resulted in the
ability of using it for forecasting purpose. If this information will be used for estimating future
values then it may result in wrong estimations that may create the issues in upcoming years.
Therefore, in order to ignore the possibility of errors or issues in future this data set should be
ignored for the purpose of forecasting (Shang, 2020).
The decision of not using the data for forecasting was taken by me after assessing the
outcomes of regression analysis. All the aspects are M square, R square, adjusted R square,
standard error etc. When all of them were assessed by me then I realised that the equation of
linear regression is providing good fit so the information or the outcomes are not good enough to
be used for forecasting (Yildiz, Bilbao and Sproul, 2017).
CONCLUSION
From the above project report it has been concluded that regression is the process of
determining the relationship strength of two different variables and one of them is required to be
dependent and another should be independent. All the results that will be generated with the help
of this process could be used for forecasting purpose so that future estimations could be made.
There are various types of elements that are focused for analysing that the relationship is strong
or not and the data is providing good fit or not. These are M square, R square, adjusted R square
and Standard error. With the help of all of them it could also be analysed that the information
should be used for future estimations or not. When good fit will be provided by the equation then
it could be used for forecasting and if the fit is not good then it could not be used for estimation.
6

REFERENCES
Books and Journals:
Angarita-Zapata, J. S., Masegosa, A. D. and Triguero, I., 2020. Evaluating automated machine
learning on supervised regression traffic forecasting problems. In Computational
Intelligence in Emerging Technologies for Engineering Applications (pp. 187-204).
Springer, Cham.
Fan, G. F., Peng, L. L. and Hong, W. C., 2018. Short term load forecasting based on phase space
reconstruction algorithm and bi-square kernel regression model. Applied energy. 224.
pp.13-33.
Fleming, S. W. and Goodbody, A. G., 2019. A Machine Learning Metasystem for Robust
Probabilistic Nonlinear Regression-Based Forecasting of Seasonal Water Availability in
the US West. IEEE Access. 7. pp.119943-119964.
Johannesen, N. J., Kolhe, M. and Goodwin, M., 2019. Relative evaluation of regression tools for
urban area electrical energy demand forecasting. Journal of cleaner production. 218.
pp.555-564.
Liang, Y., Niu, D. and Hong, W. C., 2019. Short term load forecasting based on feature
extraction and improved general regression neural network model. Energy. 166. pp.653-
663.
Shang, H. L., 2020. Dynamic principal component regression for forecasting functional time
series in a group structure. Scandinavian Actuarial Journal, 2020(4), pp.307-322.
Yildiz, B., Bilbao, J. I. and Sproul, A. B., 2017. A review and analysis of regression and machine
learning models on commercial building electricity load forecasting. Renewable and
Sustainable Energy Reviews. 73. pp.1104-1122.
7