CBMA2103 Discrete Mathematics Assignment, May 2018 - Solutions

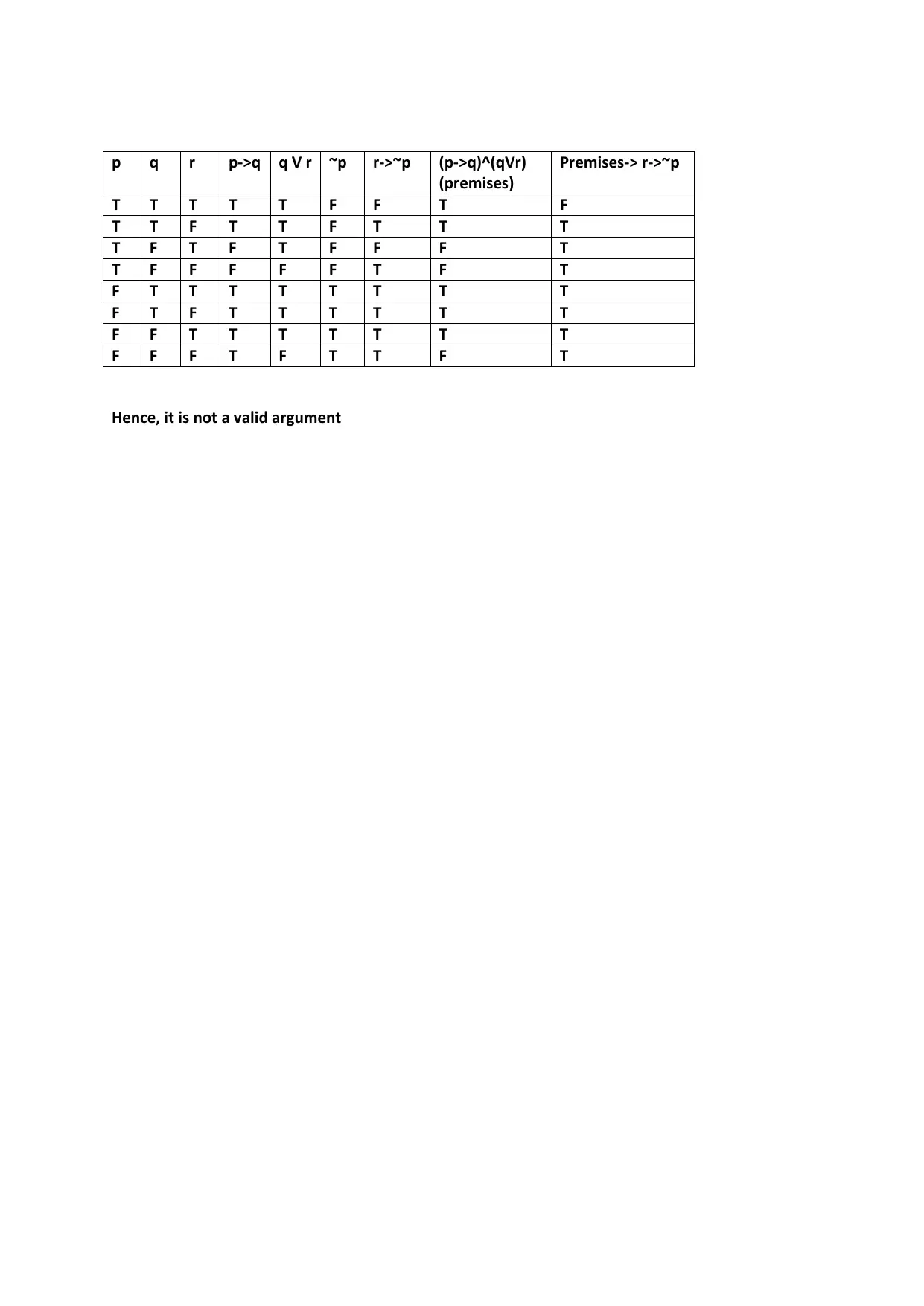
This assignment solution covers fundamental concepts in Discrete Mathematics. It includes problems related to set theory, relations, and logic. The solution demonstrates how to calculate the number of students taking specific courses using set operations, analyzes relations for reflexivity, symmetry, and transitivity to determine if they are equivalence relations, and evaluates logical statements for tautologies, contradictions, and the validity of arguments. The assignment provides detailed step-by-step solutions for each problem.

Ans1. (a)
n(M)=300
n(P)=350
n(C)=450
n(M^P)=100
n(M^C)=150
n(P^C)=75
n(M^P^C)=10
Number of students taking exactly one of those courses
= n(M) + n(P) + n(C) - n(M^P) -{ n(M^C)- n(M^P^C)} -{ n(P^C)- n(M^P^C)}
= 300+350+450-100-{150-10}-{75-10}
=795
(b)
M=300
C=450P=350

Ans2. Number of total students= 30
Number of students take statistics(S) but not accounting (A) = n(S-A) = 40% of 30 =12
Number of of the students take both statistics and accounting=n(S^A) = 30% of 30 = 9
One student does not take any of the courses.
Now,
n (S V A)=29
So, n(S)=n(S-A)+n(S^A)=12+9=21
Or n(S V A)=n(S)+n(A) – n(S^A)
Or 29=21+ n(A)-9
Or n(A)= 17
(a)
Accounting=17 Statistics=21

(b)
Number of students who take accounting and not statistics
= n(A-S)
=n(A)- n(A^S)
=17- 9
=8
(c)
Number of students who take statistics or accounting
n(S V A)-n(S^A)
=29 – 9
=20
Number of students who take statistics or accounting or both
=n(S V A)
= n(S)+ n(A) -n(S^A)
=21+17 – 9
=29
Ans3.
(a) R= {(14,10),(18,10), (20,10),(18,14),(20,14)}
Domain(R)={14,18,20,18,20}
Range (R)={10,14}
(b)
R={(1,1),(1,7),(7,1),(7,7),(2,2),(2,4),(4,2),(4,4)}
Since R is reflexive, symmetric and transitive; so R is an equivalence relation.

Ans4.
(a)
p q
p V
q p ^
q ~ (
p ^
q) (
p V
q) V ~
(
p ^
q)
T T T T F T
T F T F T T
F T T F T T
F F F F T T
Hence it is a tautology
(b)
p q (pVq) ~(pVq)
p ^ ~ (
p V
q)
T T T F F
T F T F F
F T T F F
F F F T F
Hence it is a contradiction
(c)
Let,
p= I like mathematics
q= I study mathematics
r= I fail the course
p -> q
q V r
--------------
R -> ~p

p q r p->q q V r ~p r->~p (p->q)^(qVr)
(premises)
Premises-> r->~p
T T T T T F F T F
T T F T T F T T T
T F T F T F F F T
T F F F F F T F T
F T T T T T T T T
F T F T T T T T T
F F T T T T T T T
F F F T F T T F T
Hence, it is not a valid argument