CBMA2103 Discrete Mathematics Assignment: Set Theory and Logic

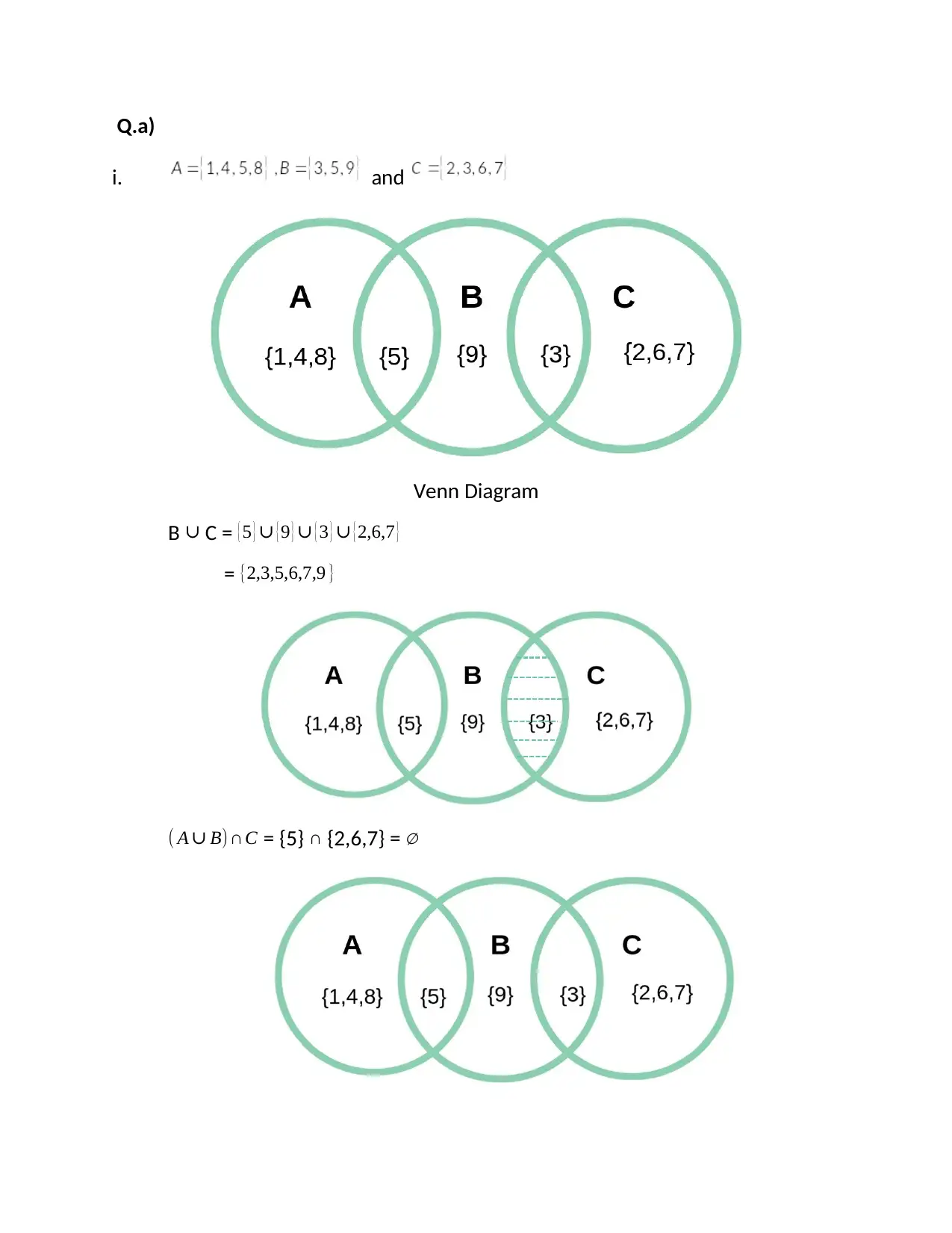
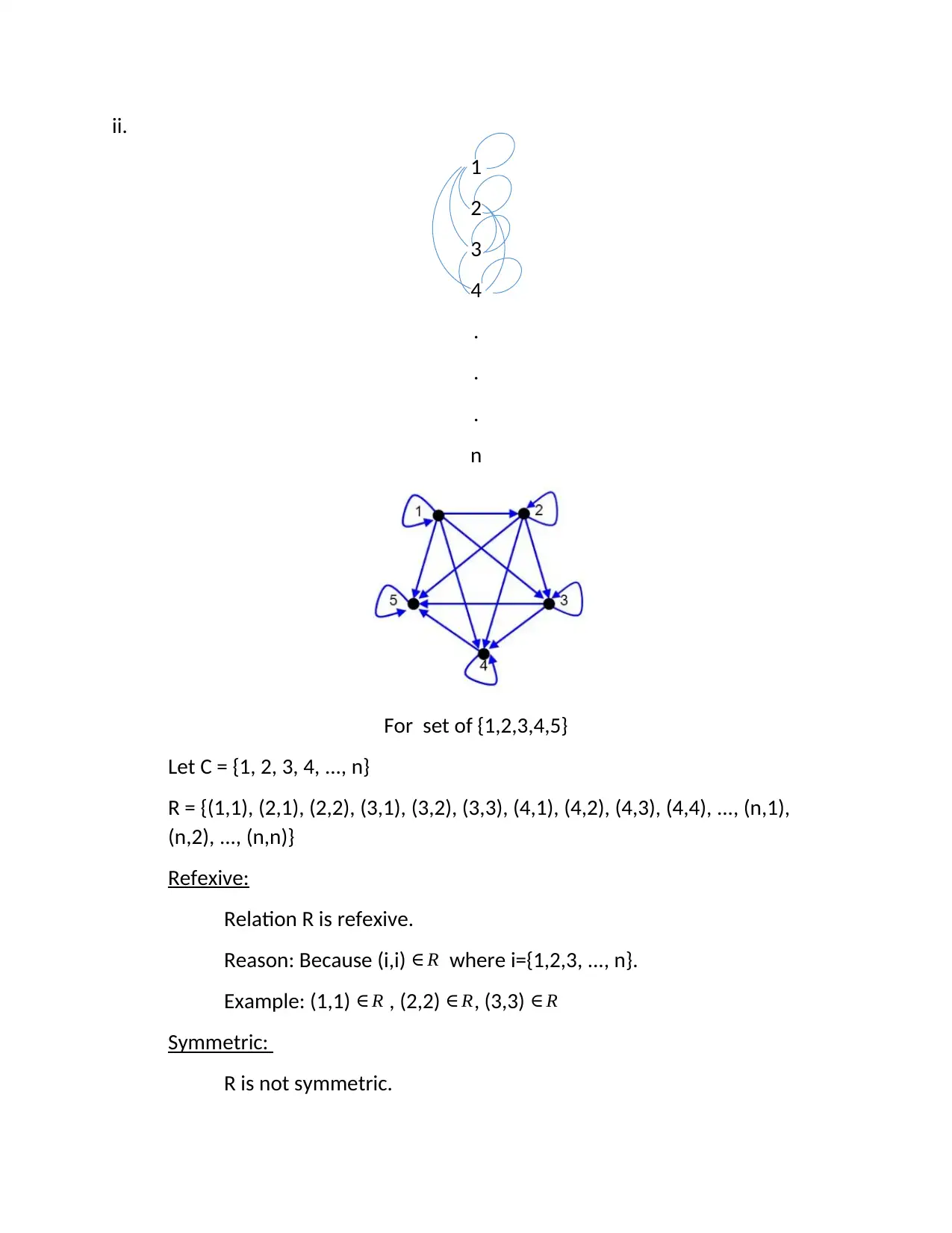
This document presents a solution to a Discrete Mathematics assignment, focusing on set theory, relations, and logic. The solution includes problems involving Venn diagrams and set operations, determining the properties of a relation (reflexive, symmetric, transitive), and translating statements into symbolic logic using quantifiers and connectives. Furthermore, it covers finding the converse, contrapositive, and negation of a given logical statement. The assignment solution is available on Desklib, a platform offering a wide range of study resources, including past papers and solved assignments, designed to support students in their academic endeavors.

Q.a)
i. and
Venn Diagram
B ∪ C = { 5 } ∪ { 9 } ∪ { 3 } ∪ { 2,6,7 }
= {2,3,5,6,7,9 }
( A ∪ B)∩C = {5} ∩ {2,6,7} = ∅

ii.
1
2
3
4
.
.
.
n
For set of {1,2,3,4,5}
Let C = {1, 2, 3, 4, ..., n}
R = {(1,1), (2,1), (2,2), (3,1), (3,2), (3,3), (4,1), (4,2), (4,3), (4,4), ..., (n,1),
(n,2), ..., (n,n)}
Refexive:
Relation R is refexive.
Reason: Because (i,i) ∈ R where i={1,2,3, ..., n}.
Example: (1,1) ∈ R , (2,2) ∈ R, (3,3) ∈ R
Symmetric:
R is not symmetric.

Reason: Because if ∀(i,j) ∈ R there is ∃( j , i)∉ R
Example: (1,2) ∈ R but ( 2,1 ) ∉ R.
Transitive:
R is transitive.
Reason: Transitive property: if a=b and b=c then a=c.Here the
property holds true: if (i,j) ∈ R and (j,k) ∈ R then (i,k)∈ R. Since, j <= i
and k<= j then i <= k. Therfore relation (i,k) exists in the set R.
Example: (4,2) ∈ R and (2,1) ∈ R then (4,1) ∈ R
Q.b)
B(p) : printer ‘p’ is busy
Q(j) : print job ‘j’ is queued
i. If every printer is busy, then there is a job in queue:
( ∀ p B ( p ) ) →(∃ jQ( j))
The Proposition:
1. printer is busy
2. job is in queue
The quantifiers:
1. ∀ : For all
2. ∃ : there exists
The connectives:
1. : negation
2. → : if ... then
ii. Converse:
In words: if there is a queued job, then every printer is busy.
In symbol: (∃ jQ( j))→ ( ∀ p B ( p ) )
Contrapositive:

In words: ifc there is no queued job, then every printer is not busy.
In symbol: (∃ j Q( j)) → ( ∀ p B ( p ) )
Simplified Contrapositive:
In words: If for all jobs are not queued, then there exists a printer
which is not busy.
In symbol: ( ∀ j Q( j)) → ( ∃ p B ( p ) )
Negation:
In words: If every printer is busy, then there does not exist a job
which is queued.
In symbols: ( ∀ p B ( p ) ) → (∃ jQ( j))
Simplified Negation:
In words: If every printer is busy, then for every job no one is queued.
In symbol: ( ∀ p B ( p ) ) →( ∀ j Q ( j))