Signals and Systems - Assignment Solutions, Analysis, and Explanation
VerifiedAdded on 2022/09/01
|6
|284
|17
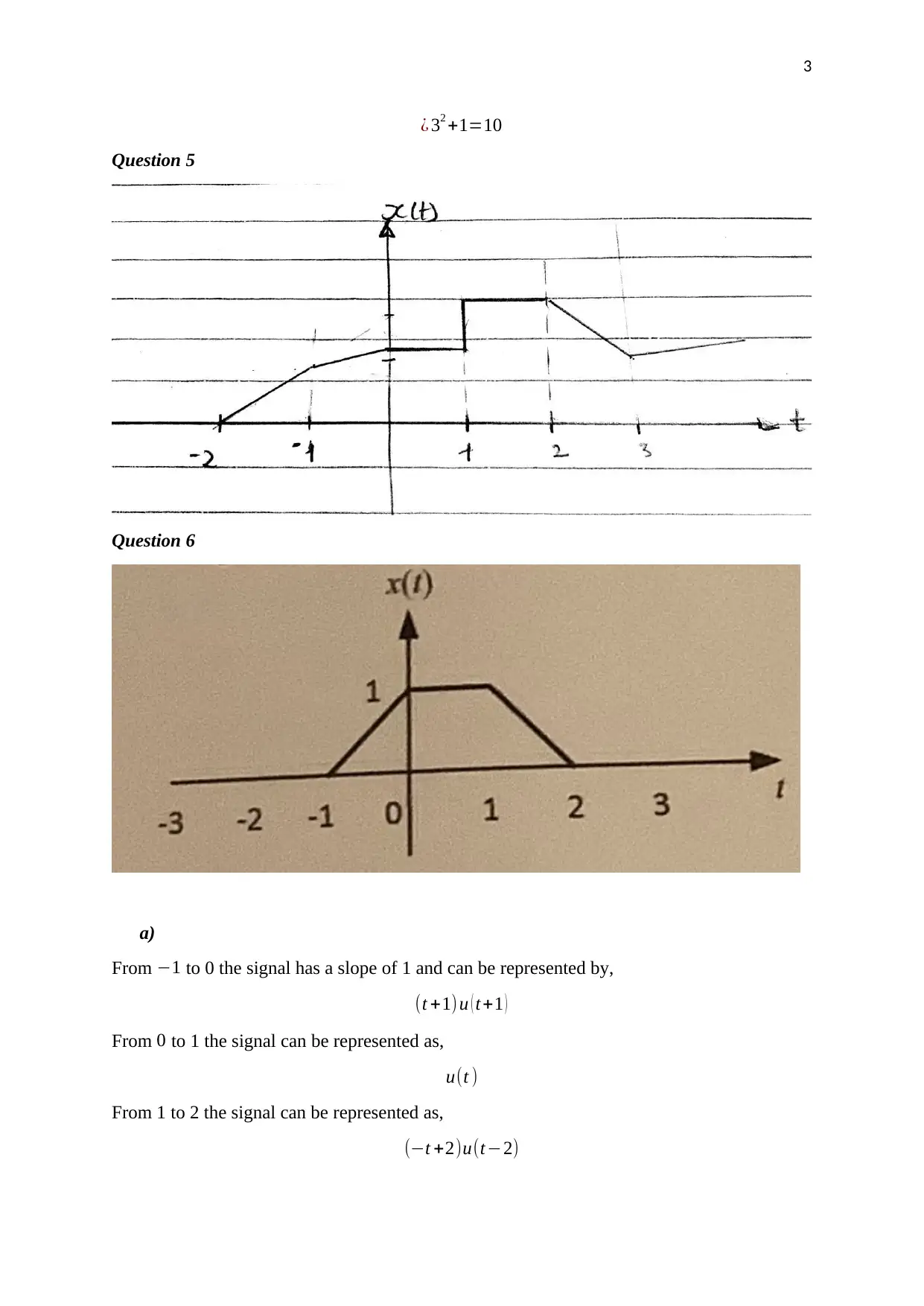
Homework Assignment
AI Summary
This document presents solutions and analysis for a Signals and Systems homework assignment. The assignment covers topics such as signal representation, system properties (linearity, causality, and memoryless systems), and mathematical analysis of signals. Specific problems include signal characterization, piecewise function definition, and system classification based on their properties. The solutions include detailed explanations and mathematical derivations. The document also references several textbooks and academic resources related to the subject. The assignment is designed to help students understand and apply fundamental concepts in signals and systems. Desklib provides access to this and other solved assignments for students to aid in their studies.
1 out of 6












![[object Object]](/_next/static/media/star-bottom.7253800d.svg)