Simulation Based Decision-Making: Limitations, Assumptions, and Results

This article discusses the limitations and assumptions of simulation based decision-making for Desklib, specifically in a medical setting. It includes a simulation worksheet with calculations for average waiting time and probability of waiting for patients. The article also includes line graphs to show simulation errors for different numbers of patients.

Simulation Based Decision-Making
Question 1
Limitations and Assumptions
a) The presences of idleness when either the doctor or nurse is not with a patient. The doctor
will choice to take his time if most of the patients wait to see the nurse instead of
attending to the patients that want to see him
b) The lack of a defined queuing system that will allow the patients to efficiency optimize
on the immediate availability of a doctor or nurse to ensure that there is no time wastage.
c) In the computations the patients who arrived later on after the doctor or nurse was free
were given negative waiting time values which were corrected to negative values.
Part 1
The simulation is in Microsoft Excel document worksheet 1 (simulation work 1.xlx). It can be
represented with the image below
Customer Rand Number 1Interval Arrival TimeRand Number 2 Attention Needed Rand Number 3Doctor AloneRand Number 4Nurse AloneRand Number 5Both Finish Time Time in SystemWait Time Corrected Time Wait
1 0.44087 15 15 0.694677488 Nurse Alone 0.097233 0 0.107712 15 0.642628 0 30 15 0 0
2 0.230984 10 25 0.929922464 Both 0.206246 0 0.571922 0 0.884428 35 60 35 5 5
3 0.097423 5 30 0.969370267 Both 0.91886 0 0.192084 0 0.139362 20 50 20 30 30
4 0.529403 20 50 0.386345424 Doctor Alone 0.597812 20 0.007069 0 0.171933 0 70 20 0 0
5 0.36631 15 65 0.753767337 Both 0.426594 0 0.772586 0 0.959538 40 105 40 5 5
6 0.357304 15 80 0.877063414 Both 0.666564 0 0.375092 0 0.630805 30 110 30 25 25
7 0.073742 5 85 0.71570429 Nurse Alone 0.139228 0 0.163264 15 0.084947 0 100 15 25 25
8 0.325105 15 100 0.126098468 Doctor Alone 0.429451 15 0.282234 0 0.164914 0 115 15 0 0
9 0.898469 25 125 0.402582944 Nurse Alone 0.321872 0 0.889334 25 0.060909 0 150 25 -10 0
10 0.559151 20 145 0.006453041 Doctor Alone 0.777579 25 0.821338 0 0.252788 0 170 25 5 5
11 0.218113 10 155 0.440252773 Nurse Alone 0.126611 0 0.127099 15 0.671377 0 170 15 15 15
12 0.482109 20 175 0.808793215 Both 0.920978 0 0.106238 0 0.104713 20 195 20 -5 0
13 0.05723 5 180 0.044400201 Doctor Alone 0.828882 25 0.811109 0 0.888883 0 205 25 15 15
14 0.493122 20 200 0.99092875 Both 0.330882 0 0.589671 0 0.507184 30 230 30 5 5
15 0.386081 15 215 0.118736311 Doctor Alone 0.77418 25 0.404653 0 0.749301 0 240 25 15 15
16 0.815061 25 240 0.682019046 Nurse Alone 0.155139 0 0.580259 20 0.821624 0 260 20 0 0
17 0.642938 20 260 0.349564488 Doctor Alone 0.104647 10 0.776685 0 0.14783 0 270 10 0 0
18 0.100323 10 270 0.07290249 Doctor Alone 0.788847 25 0.469654 0 0.473794 0 295 25 0 0
19 0.142609 10 280 0.945896252 Both 0.866867 0 0.767478 0 0.860919 35 315 35 15 15
20 0.534276 20 300 0.241246841 Doctor Alone 0.935454 30 0.674239 0 0.042317 0 330 30 15 15
21 0.739647 25 325 0.630496824 Nurse Alone 0.699229 0 0.311921 15 0.836785 0 340 15 5 5
22 0.561989 20 345 0.912982061 Both 0.674433 0 0.472861 0 0.837923 35 380 35 -5 0
23 0.426237 15 360 0.56241471 Nurse Alone 0.895198 0 0.467916 20 0.507331 0 380 20 20 20
24 0.211013 10 370 0.891865187 Both 0.955219 0 0.356228 0 0.348122 25 395 25 10 10
25 0.23966 10 380 0.205010005 Doctor Alone 0.552872 20 0.11124 0 0.334909 0 400 20 15 15
26 0.255333 15 395 0.888880452 Both 0.693233 0 0.242688 0 0.127131 20 415 20 5 5
27 0.275208 15 410 0.540694888 Nurse Alone 0.233778 0 0.595368 20 0.734773 0 430 20 5 5
28 0.566085 20 430 0.506812477 Nurse Alone 0.784286 0 0.191861 15 0.888965 0 445 15 0 0
29 0.26544 15 445 0.73970667 Nurse Alone 0.842607 0 0.894591 25 0.279048 0 470 25 0 0
30 0.792525 25 470 0.518586105 Nurse Alone 0.961114 0 0.028376 10 0.348839 0 480 10 0 0
31 0.828251 25 495 0.524040166 Nurse Alone 0.713926 0 0.661852 20 0.571825 0 515 20 -15 0
32 0.688788 20 515 0.385676903 Doctor Alone 0.56876 20 0.492327 0 0.458826 0 535 20 0 0
33 0.075108 5 520 0.251313392 Doctor Alone 0.464925 15 0.730966 0 0.516804 0 535 15 15 15
34 0.373228 15 535 0.089160745 Doctor Alone 0.541841 20 0.116339 0 0.180094 0 555 20 0 0
35 0.795096 25 560 0.238594477 Doctor Alone 0.67882 20 0.371495 0 0.677709 0 580 20 -5 0
36 0.020433 5 565 0.964197156 Both 0.09964 0 0.249479 0 0.807316 35 600 35 15 15
37 0.359388 15 580 0.949508249 Both 0.399016 0 0.77148 0 0.863345 35 615 35 20 20
38 0.265024 15 595 0.564265254 Nurse Alone 0.599452 0 0.542398 20 0.440959 0 615 20 20 20
39 0.298908 15 610 0.748114031 Nurse Alone 0.650693 0 0.708653 20 0.431708 0 630 20 5 5
40 0.257182 15 625 0.603941239 Nurse Alone 0.623537 0 0.346217 15 0.636216 0 640 15 5 5
41 0.747398 25 650 0.650161178 Nurse Alone 0.213743 0 0.838335 20 0.77056 0 670 20 -10 0
42 0.001315 5 655 0.186659146 Doctor Alone 0.288115 15 0.066816 0 0.117337 0 670 15 15 15
43 0.892223 25 680 0.790497798 Both 0.401791 0 0.105141 0 0.510911 30 710 30 -10 0
44 0.943129 30 710 0.351255187 Doctor Alone 0.154388 10 0.766104 0 0.35664 0 720 10 0 0
45 0.611222 20 730 0.595755351 Nurse Alone 0.763177 0 0.956957 25 0.308955 0 755 25 -10 0
46 0.365035 15 745 0.011151619 Doctor Alone 0.027652 10 0.146557 0 0.774581 0 755 10 10 10
47 0.407561 15 760 0.589330025 Nurse Alone 0.545781 0 0.604298 20 0.772409 0 780 20 -5 0
48 0.552294 20 780 0.456161139 Nurse Alone 0.683113 0 0.156849 15 0.631072 0 795 15 0 0
49 0.11524 10 790 0.365630616 Doctor Alone 0.529141 20 0.837752 0 0.330035 0 810 20 5 5
50 0.708327 20 810 0.178941904 Doctor Alone 0.455669 15 0.822863 0 0.003626 0 825 15 0 0

Part 2
But adding an extra 1950 simulations we are able to better estimate the average 2waiting time as
welll as average probability of waiting. The extra 1950 simulations are faded out to pay keen
emphasises on the 50 main simulation. However, the average of waiting time and probability will
be taken from all 2000 simulations. Therefore, the average waiting time is roughly 6 minutes,
and the probability that a patient will have to wait is roughly 0.5 or 50% .
The calculations are also in worksheet 1 of (simulation work 1.xlx). They are given by the
following image
10 1
0 0
0 0
10 1
15 1
15 1
0 0
6.0125 0.522
Average Wait Time Average Probability
Part 3.
By plotting the simulation errors on a line graph we are able to recognize where the simulation
fails as the line becomes more flat. Hence, there are three graphs for 2000, 300, and 150 patients
respectively. it is therefore clear that the optimum minimum number of patients is roughly 150
patients . The calculations are also in worksheet 1 of (simulation work 1.xlx).

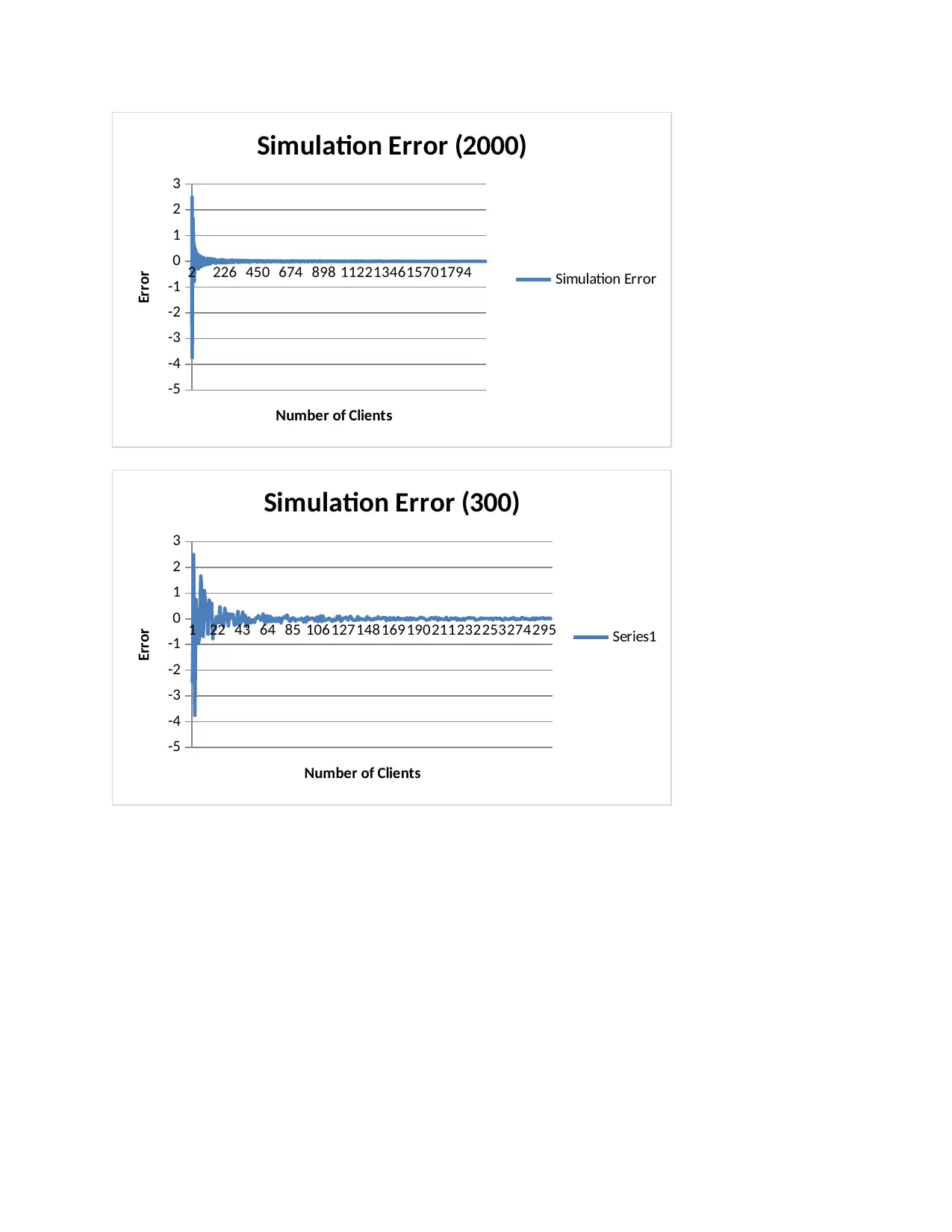
2 226 450 674 898 1122134615701794
-5
-4
-3
-2
-1
0
1
2
3
Simulation Error (2000)
Simulation Error
Number of Clients
Error
1 22 43 64 85 106127148169190211232253274295
-5
-4
-3
-2
-1
0
1
2
3
Simulation Error (300)
Series1
Number of Clients
Error

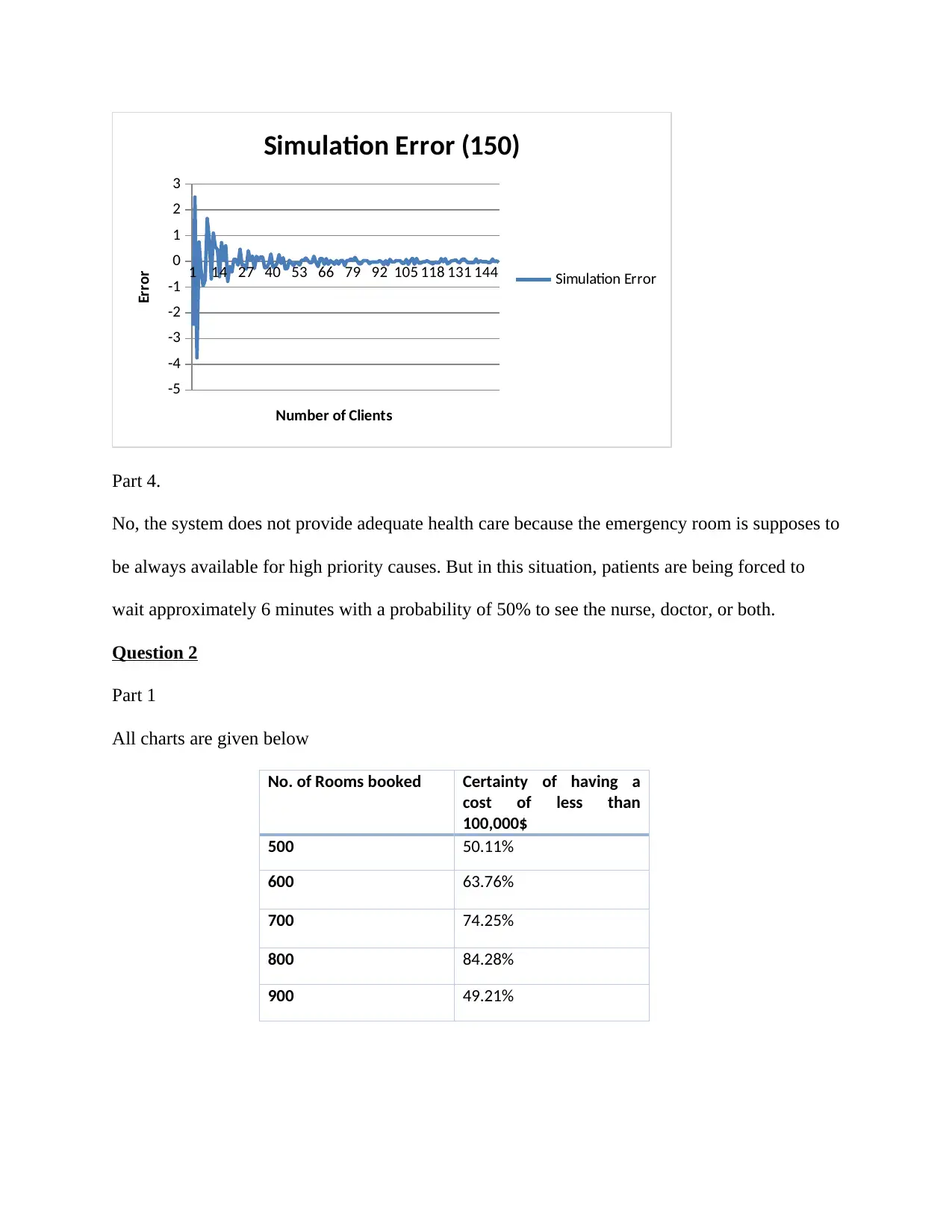
1 14 27 40 53 66 79 92 105 118 131 144
-5
-4
-3
-2
-1
0
1
2
3
Simulation Error (150)
Simulation Error
Number of Clients
Error
Part 4.
No, the system does not provide adequate health care because the emergency room is supposes to
be always available for high priority causes. But in this situation, patients are being forced to
wait approximately 6 minutes with a probability of 50% to see the nurse, doctor, or both.
Question 2
Part 1
All charts are given below
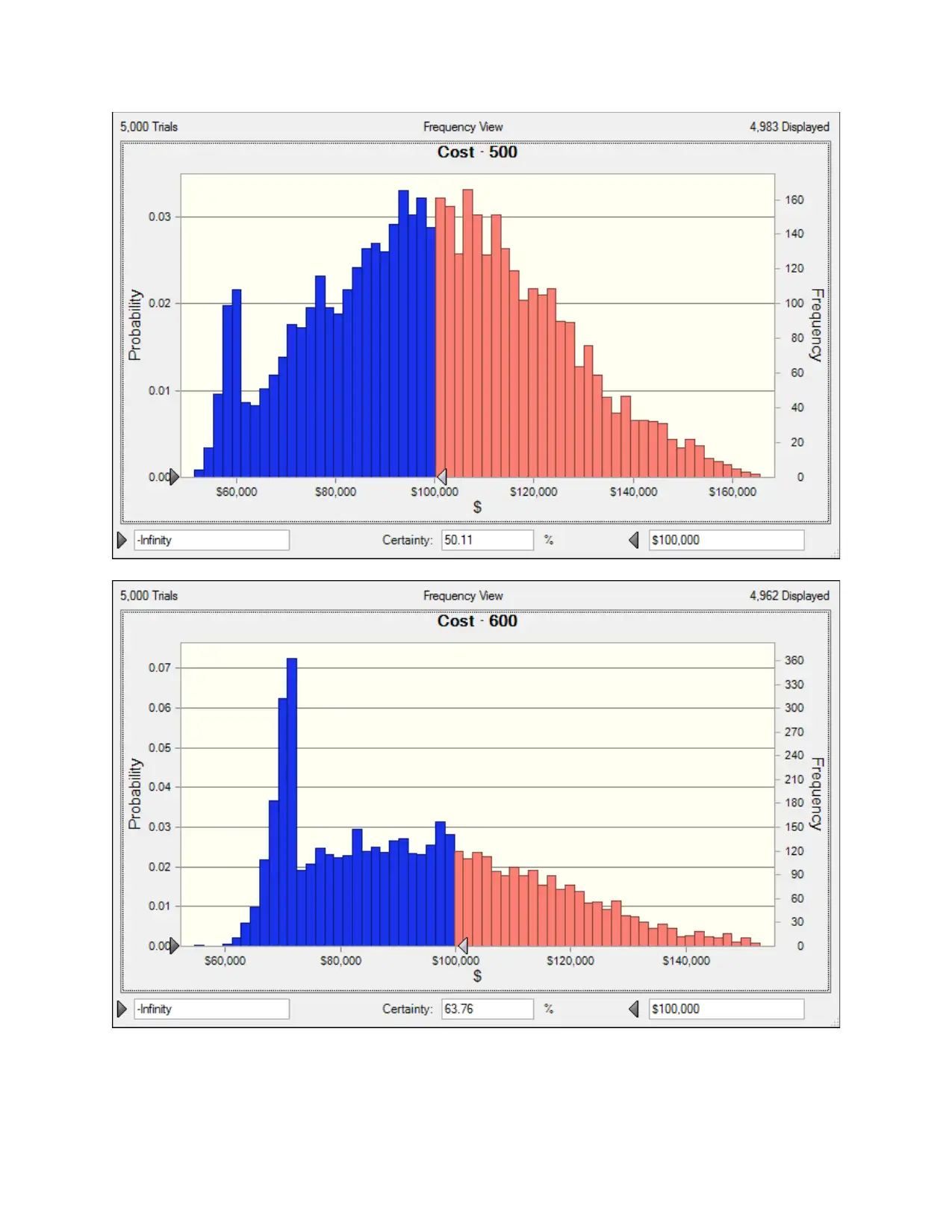
No. of Rooms booked Certainty of having a
cost of less than
100,000$
500 50.11%
600 63.76%
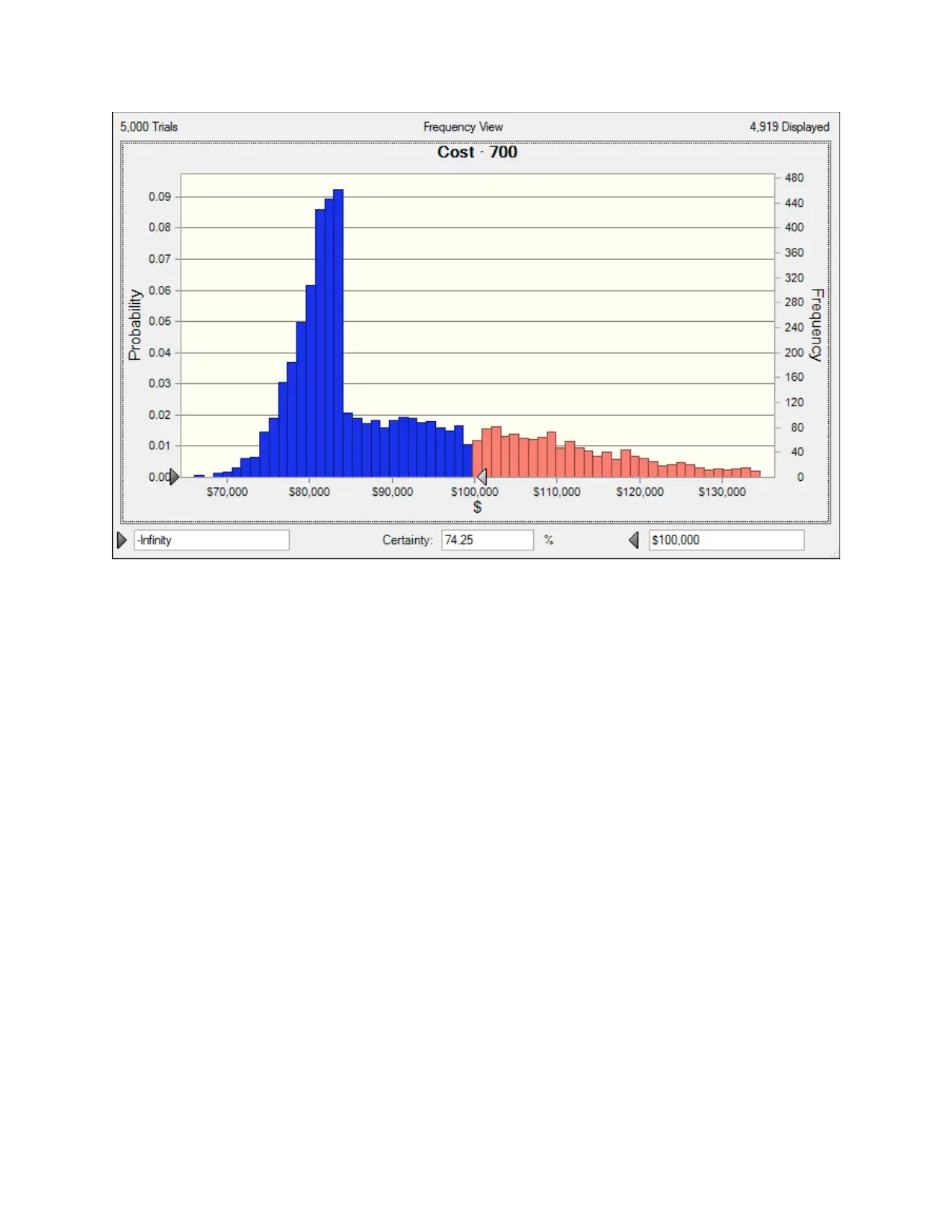
700 74.25%
800 84.28%
900 49.21%

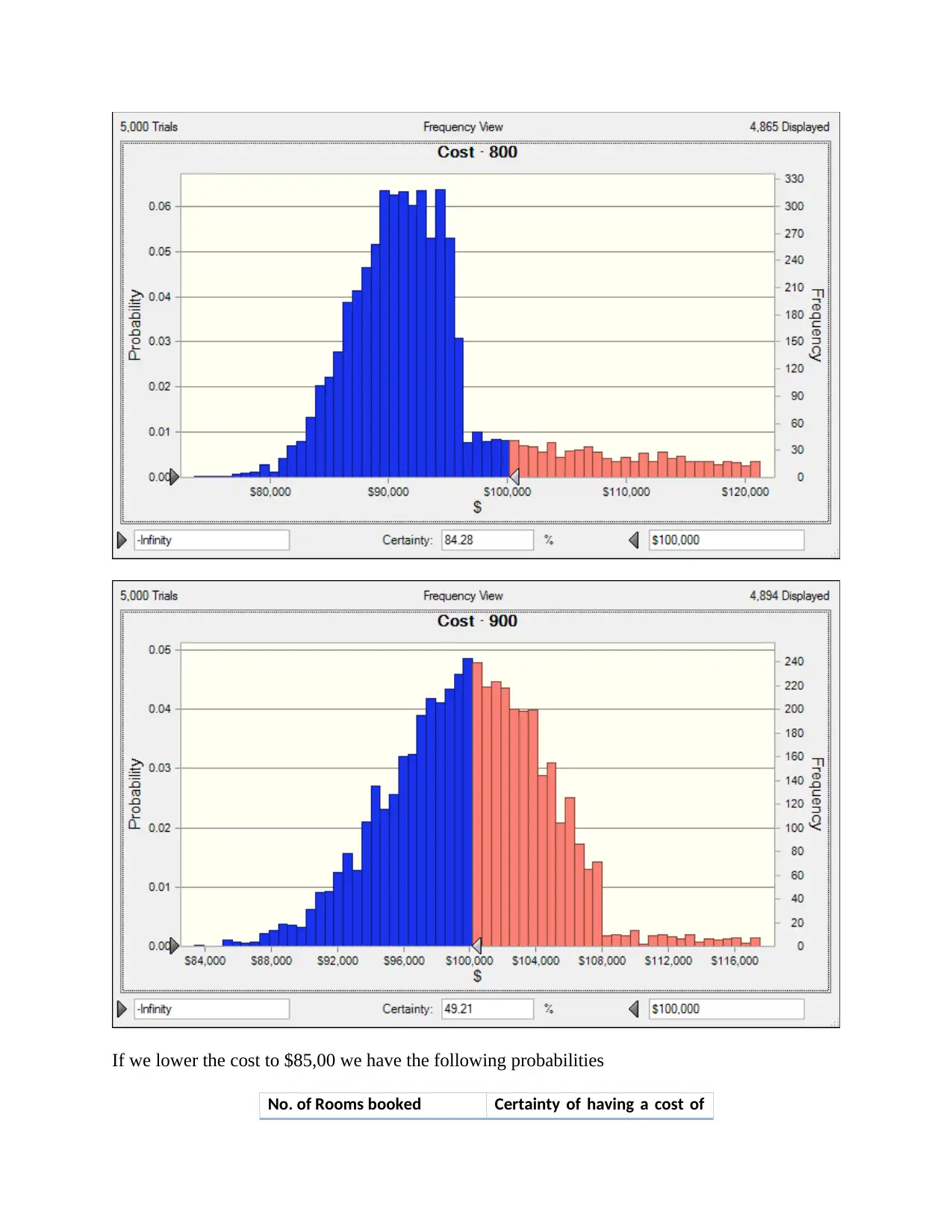
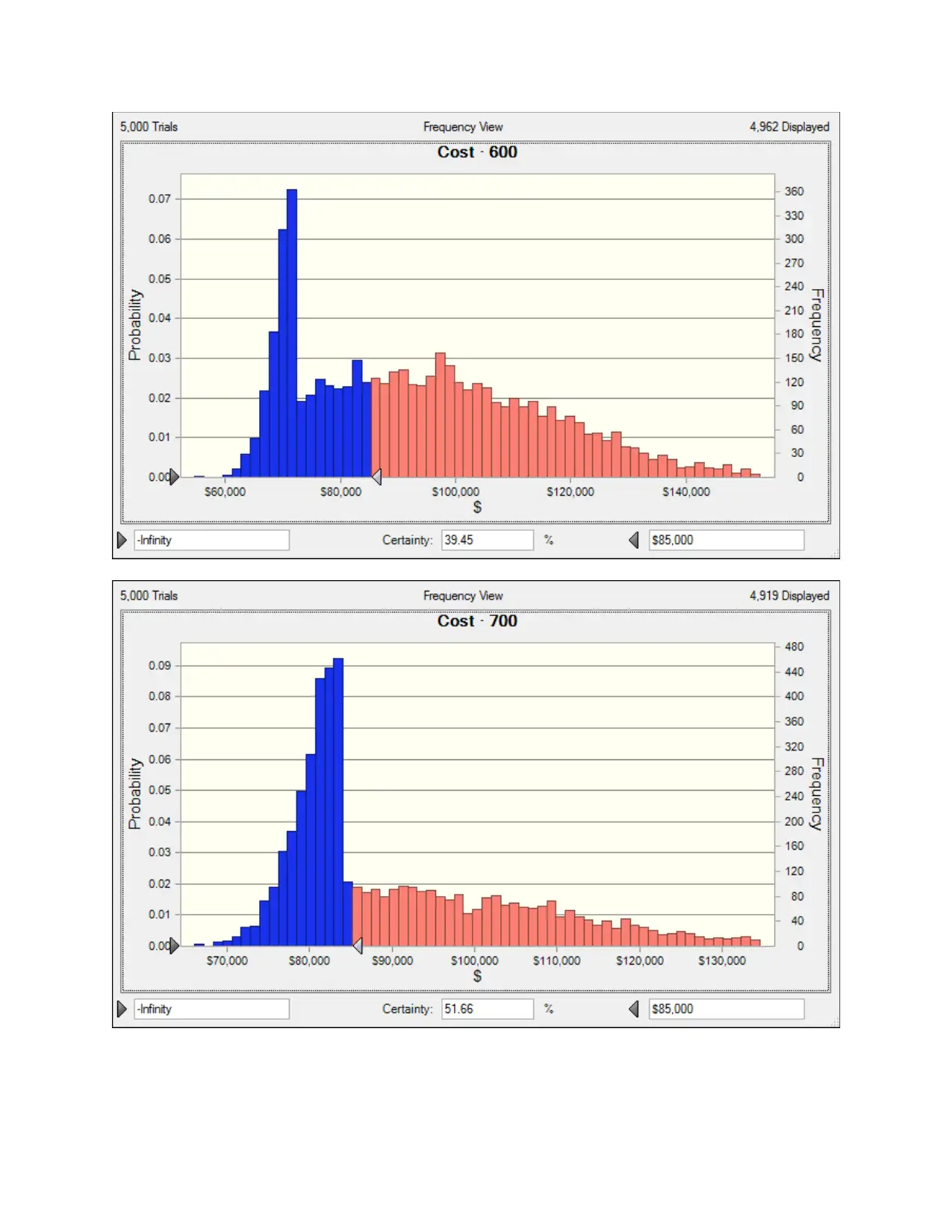
If we lower the cost to $85,00 we have the following probabilities
No. of Rooms booked Certainty of having a cost of

less than 85,000$
600 39.45%
700 51.66%
800 7.17%

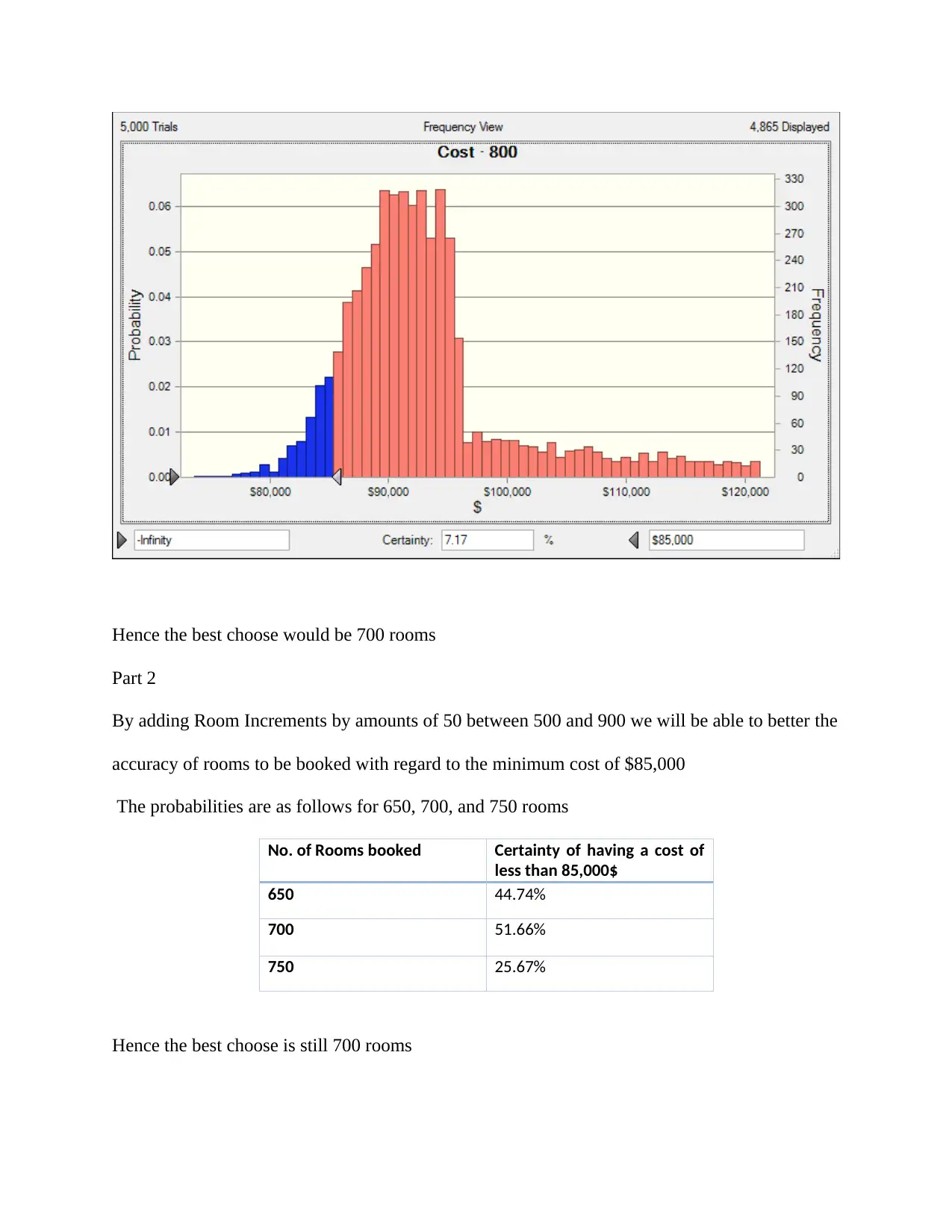
Hence the best choose would be 700 rooms
Part 2
By adding Room Increments by amounts of 50 between 500 and 900 we will be able to better the
accuracy of rooms to be booked with regard to the minimum cost of $85,000
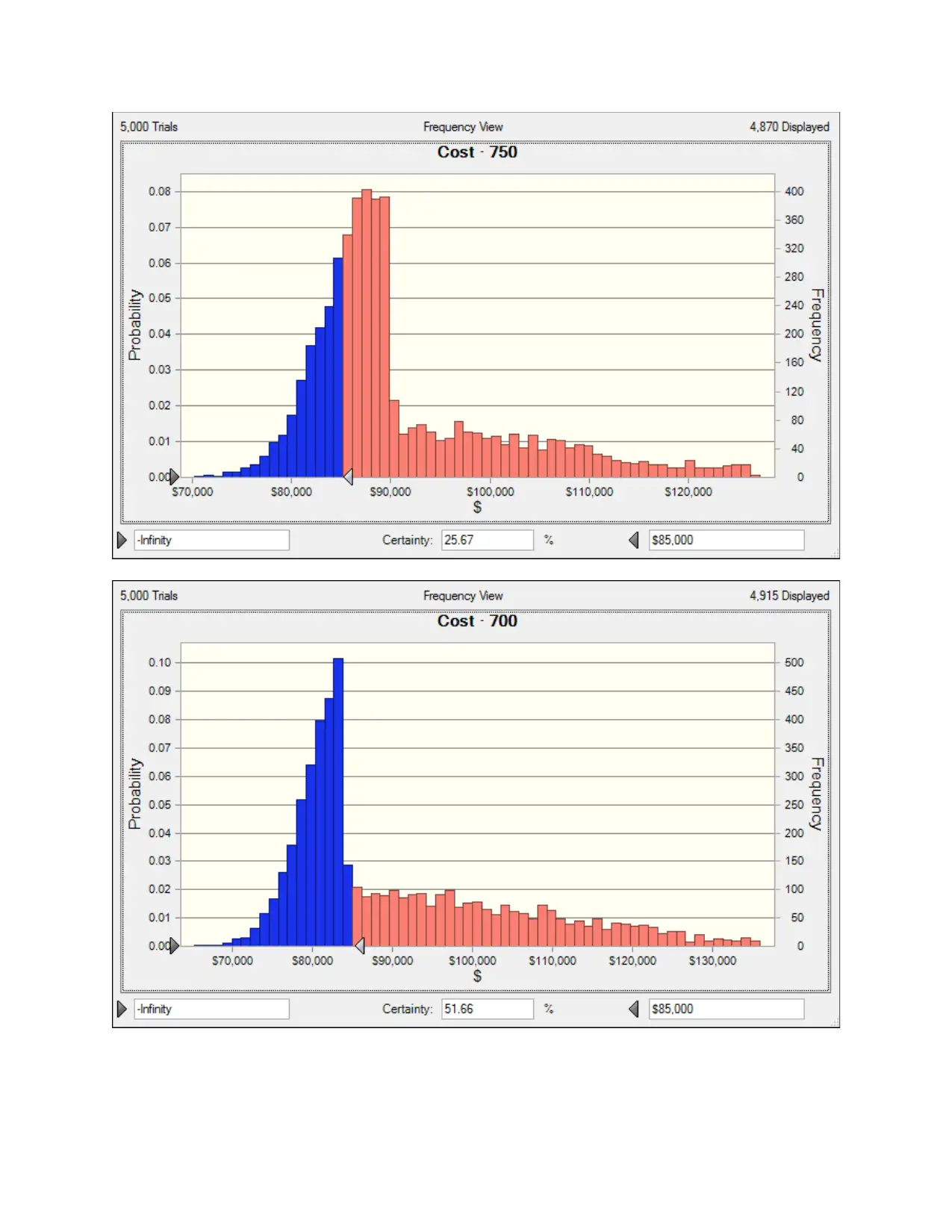
The probabilities are as follows for 650, 700, and 750 rooms
No. of Rooms booked Certainty of having a cost of
less than 85,000$
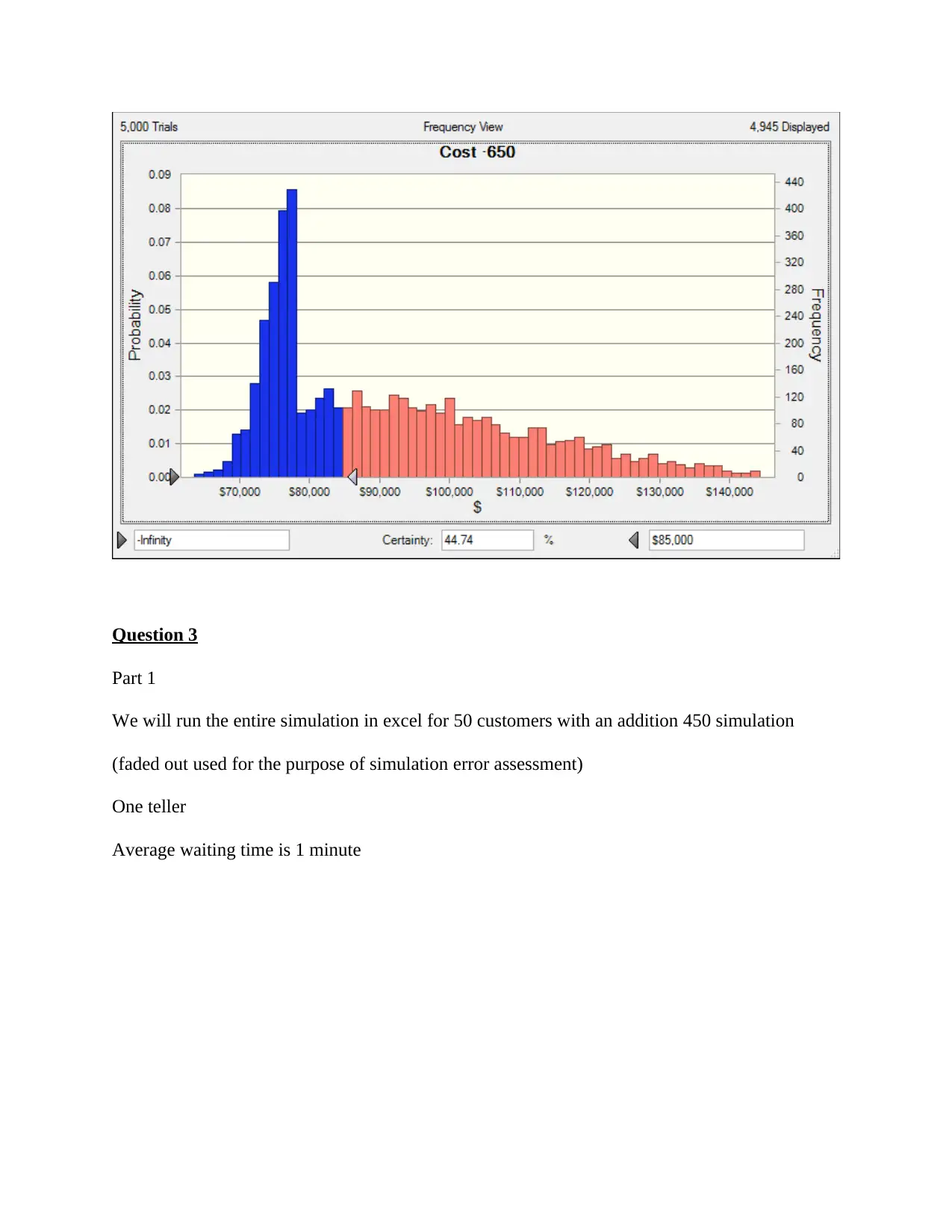
650 44.74%
700 51.66%
750 25.67%
Hence the best choose is still 700 rooms

Question 3
Part 1
We will run the entire simulation in excel for 50 customers with an addition 450 simulation
(faded out used for the purpose of simulation error assessment)
One teller
Average waiting time is 1 minute

Customer Rand 1 Interval Arrival Time Average Arrival Simulation Error Rand 2 Service time Finish Time Time In system Waiting Time Corrected Waiting Time
1 0.375499 3 3 3 0 0.632962 4 7 4 0 0
2 0.419051 3 6 3 0 0.390451 3 9 3 1 1
3 0.465245 3 9 3 -0.25 0.267262 3 12 3 0 0
4 0.23253 2 11 2.75 0.25 0.215614 3 14 3 1 1
5 0.818447 4 15 3 0.166666667 0.329595 3 18 3 -1 0
6 0.718479 4 19 3.166666667 0.119047619 0.675364 4 23 4 -1 0
7 0.710678 4 23 3.285714286 -0.160714286 0.425689 3 26 3 0 0
8 0.081687 2 25 3.125 -0.013888889 0.398491 3 28 3 1 1
9 0.37876 3 28 3.111111111 -0.111111111 0.65869 4 32 4 0 0
10 0.212619 2 30 3 -0.090909091 0.090538 2 32 2 2 2
11 0.1026 2 32 2.909090909 -0.075757576 0.032306 2 34 2 0 0
12 0.146625 2 34 2.833333333 0.012820513 0.573989 4 38 4 0 0
13 0.42773 3 37 2.846153846 0.010989011 0.595693 4 41 4 1 1
14 0.555267 3 40 2.857142857 0.00952381 0.616739 4 44 4 1 1
15 0.64302 3 43 2.866666667 0.008333333 0.361028 3 46 3 1 1
16 0.526049 3 46 2.875 -0.051470588 0.521002 4 50 4 0 0
17 0.032863 2 48 2.823529412 0.009803922 0.118995 3 51 3 2 2
18 0.608172 3 51 2.833333333 0.00877193 0.949487 6 57 6 0 0
19 0.315946 3 54 2.842105263 0.007894737 0.918782 6 60 6 3 3
20 0.428192 3 57 2.85 0.054761905 0.132732 3 60 3 3 3
21 0.810183 4 61 2.904761905 0.004329004 0.460617 3 64 3 -1 0
22 0.482165 3 64 2.909090909 -0.039525692 0.39002 3 67 3 0 0
23 0.17714 2 66 2.869565217 -0.036231884 0.464739 3 69 3 1 1
24 0.078272 2 68 2.833333333 0.086666667 0.252607 3 71 3 1 1
25 0.982771 5 73 2.92 0.08 0.378717 3 76 3 -2 0
26 0.905623 5 78 3 0.074074074 0.051175 2 80 2 -2 0
27 0.977614 5 83 3.074074074 -0.002645503 0.115877 3 86 3 -3 0
28 0.30127 3 86 3.071428571 0.032019704 0.90719 6 92 6 0 0
29 0.796434 4 90 3.103448276 0.029885057 0.861913 5 95 5 2 2
30 0.805129 4 94 3.133333333 -0.03655914 0.337269 3 97 3 1 1
31 0.170983 2 96 3.096774194 0.028225806 0.37593 3 99 3 1 1
32 0.853134 4 100 3.125 -0.034090909 0.176147 3 103 3 -1 0
33 0.091272 2 102 3.090909091 -0.002673797 0.014884 2 104 2 1 1
34 0.563985 3 105 3.088235294 -0.002521008 0.825271 5 110 5 -1 0
35 0.609434 3 108 3.085714286 -0.03015873 0.888631 5 113 5 2 2
36 0.054207 2 110 3.055555556 -0.001501502 0.777823 5 115 5 3 3
37 0.394108 3 113 3.054054054 -0.001422475 0.38993 3 116 3 2 2
38 0.406881 3 116 3.052631579 -0.001349528 0.194412 3 119 3 0 0
39 0.334439 3 119 3.051282051 -0.001282051 0.226808 3 122 3 0 0
40 0.367412 3 122 3.05 -0.001219512 0.276559 3 125 3 0 0
41 0.69052 3 125 3.048780488 0.046457607 0.96719 6 131 6 0 0
42 0.938151 5 130 3.095238095 -0.002214839 0.159734 3 133 3 1 1
43 0.554979 3 133 3.093023256 -0.024841438 0.386369 3 136 3 0 0
44 0.061588 2 135 3.068181818 -0.001515152 0.007404 2 137 2 1 1
45 0.30922 3 138 3.066666667 0.020289855 0.920981 6 144 6 -1 0
46 0.750281 4 142 3.086956522 0.019426457 0.687826 4 146 4 2 2
47 0.755878 4 146 3.106382979 -0.002216312 0.686935 4 150 4 0 0
48 0.313262 3 149 3.104166667 -0.00212585 0.212368 3 152 3 1 1
49 0.62457 3 152 3.102040816 -0.002040816 0.140425 3 155 3 0 0
50 0.493018 3 155 3.1 0.037254902 0.797085 5 160 5 0 0
Two tellers
Average waiting time is 5 seconds

Customer Rand 1 Interval Arrival TimeAverage ArrivalSimulation ErrorRand 2 Service time Finish Time Time In system Waiting TimeCorrected Waiting Time
1 0.372349 3 3 3 0 0.57786188 2 5 2 0 0
2 0.974108 5 8 4 -0.66667 0.57851065 2 10 2 -3 0
3 0.08932 2 10 3.333333 -0.33333 0.1547396 1.5 11.5 1.5 0 0
4 0.125958 2 12 3 0 0.05545955 1 13 1 -0.5 0
5 0.309117 3 15 3 -0.16667 0.71675363 2.5 17.5 2.5 -2 0
6 0.180245 2 17 2.833333 0.02381 0.19950181 1.5 18.5 1.5 0.5 0.5
7 0.673671 3 20 2.857143 -0.10714 0.82374695 2.5 22.5 2.5 -1.5 0
8 0.203661 2 22 2.75 -0.08333 0.94745066 3 25 3 0.5 0.5
9 0.047536 2 24 2.666667 0.033333 0.58347113 2 26 2 1 1
10 0.409033 3 27 2.7 -0.06364 0.41275658 1.5 28.5 1.5 -1 0
11 0.070353 2 29 2.636364 -0.05303 0.4608996 1.5 30.5 1.5 -0.5 0
12 0.139226 2 31 2.583333 0.032051 0.24760069 1.5 32.5 1.5 -0.5 0
13 0.372227 3 34 2.615385 0.027473 0.66415209 2 36 2 -1.5 0
14 0.464615 3 37 2.642857 -0.04286 0.31306302 1.5 38.5 1.5 -1 0
15 0.232466 2 39 2.6 0.025 0.23853988 1.5 40.5 1.5 -0.5 0
16 0.552748 3 42 2.625 0.080882 0.34955874 1.5 43.5 1.5 -1.5 0
17 0.882744 4 46 2.705882 -0.03922 0.52987857 2 48 2 -2.5 0
18 0.067638 2 48 2.666667 -0.03509 0.71994722 2.5 50.5 2.5 0 0
19 0.172187 2 50 2.631579 0.018421 0.75835607 2.5 52.5 2.5 0.5 0.5
20 0.264889 3 53 2.65 0.016667 0.27058255 1.5 54.5 1.5 -0.5 0
21 0.359446 3 56 2.666667 0.060606 0.44093576 1.5 57.5 1.5 -1.5 0
22 0.827064 4 60 2.727273 0.011858 0.63306203 2 62 2 -2.5 0
23 0.600218 3 63 2.73913 -0.0308 0.15421511 1.5 64.5 1.5 -1 0
24 0.048209 2 65 2.708333 -0.02833 0.63087318 2 67 2 -0.5 0
25 0.007742 2 67 2.68 0.012308 0.42446559 1.5 68.5 1.5 0 0
26 0.586583 3 70 2.692308 0.011396 0.38371801 1.5 71.5 1.5 -1.5 0
27 0.626323 3 73 2.703704 0.010582 0.54990912 2 75 2 -1.5 0
28 0.280937 3 76 2.714286 0.009852 0.27763628 1.5 77.5 1.5 -1 0
29 0.577862 3 79 2.724138 -0.02414 0.12709616 1.5 80.5 1.5 -1.5 0
30 0.221962 2 81 2.7 0.074194 0.2041685 1.5 82.5 1.5 -0.5 0
31 0.933953 5 86 2.774194 0.038306 0.69633017 2 88 2 -3.5 0
32 0.87247 4 90 2.8125 -0.02462 0.09755156 1 91 1 -2 0
33 0.229383 2 92 2.787879 0.006239 0.35606819 1.5 93.5 1.5 -1 0
34 0.456478 3 95 2.794118 0.005882 0.61703576 2 97 2 -1.5 0
35 0.623622 3 98 2.8 0.005556 0.22048733 1.5 99.5 1.5 -1 0
36 0.348937 3 101 2.805556 0.005255 0.21734365 1.5 102.5 1.5 -1.5 0
37 0.566996 3 104 2.810811 0.004979 0.6290512 2 106 2 -1.5 0
38 0.349886 3 107 2.815789 0.004723 0.96356252 3 110 3 -1 0
39 0.279581 3 110 2.820513 -0.02051 0.11667604 1.5 111.5 1.5 0 0
40 0.13317 2 112 2.8 0.004878 0.43109458 1.5 113.5 1.5 -0.5 0
41 0.513279 3 115 2.804878 -0.01916 0.81628171 2.5 117.5 2.5 -1.5 0
42 0.099232 2 117 2.785714 0.051495 0.7535876 2.5 119.5 2.5 0.5 0.5
43 0.919342 5 122 2.837209 -0.01903 0.12793531 1.5 123.5 1.5 -2.5 0
44 0.104674 2 124 2.818182 0.00404 0.64880916 2 126 2 -0.5 0
45 0.543481 3 127 2.822222 0.047343 0.32175414 1.5 128.5 1.5 -1 0
46 0.998917 5 132 2.869565 0.002775 0.80858635 2.5 134.5 2.5 -3.5 0
47 0.281222 3 135 2.87234 0.023493 0.14158326 1.5 136.5 1.5 -0.5 0
48 0.893769 4 139 2.895833 0.022534 0.37538464 1.5 140.5 1.5 -2.5 0
49 0.89981 4 143 2.918367 -0.01837 0.91406509 3 146 3 -2.5 0
50 0.220215 2 145 2.9 -0.01765 0.25740619 1.5 146.5 1.5 1 1
Part Two
The minimal simulation trials has to 250 see images below for both one and two tellers
respectively

1 20 39 58 77 96 115134153172191210229248
-0.8
-0.7
-0.6
-0.5
-0.4
-0.3
-0.2
-0.1
0
0.1
0.2
Simulation Error (250)
Simulation Error
1 20 39 58 77 96 115134153172191210229248
-0.4
-0.3
-0.2
-0.1
0
0.1
0.2
0.3
Simulation Error (250)
Simulation Error
There is a 50-50 utilization of both teller windows in the case of two-tellers being employed.
There is need to hire two-tellers because it boosts performance and reduces waiting time by 55
seconds.
Question 4
Part1

Flowchart
Customer Arrival
Queues in Line for Ticket Buffer 1
Decision
Point 1
Licensing With Sharon
Work station 3
Registration with Peter
Work station 2
Clerk Issues Ticket
Work station 1
Customer Exit
Buffer 4
45%
25%
30%
Licensing Waiting
Buffer 3
Registration Waiting
Buffer 2 12.5% 12.5%

Part 2
Simulation in SimQuick
Simulation Results
Element Element Statistics Overall
types names Means
Entrance(s) Customer Arrivals Objects entering process 44.86
Objects unable to enter 0.00
Service level 1.00
Work Station(s) Work Station 1 Final status NA
Final inventory (int. buff.) 0.00
Mean inventory (int. buff.) 0.00
Mean cycle time (int. buff.) 0.00
Work cycles started 44.81
Fraction time working 0.25
Fraction time blocked 0.00
Work Station 2 Final status NA
Final inventory (int. buff.) 0.00
Mean inventory (int. buff.) 0.00
Mean cycle time (int. buff.) 0.00
Work cycles started 17.99
Fraction time working 0.69
Fraction time blocked 0.00
Work Station 3 Final status NA
Final inventory (int. buff.) 0.00
Mean inventory (int. buff.) 0.00
Mean cycle time (int. buff.) 0.00
Work cycles started 24.74
Fraction time working 0.68
Fraction time blocked 0.00
Buffer(s) Buffer 1 Objects leaving 44.81
Final inventory 0.06
Minimum inventory 0.00
Maximum inventory 1.93
Mean inventory 0.05
Mean cycle time 0.21
Buffer 2 Objects leaving 17.99
Final inventory 0.99
Minimum inventory 0.00
Maximum inventory 3.26
Mean inventory 0.76
Mean cycle time 6.85
Buffer 3 Objects leaving 24.74
Final inventory 0.83
Minimum inventory 0.00
Maximum inventory 3.53
Mean inventory 0.71
Mean cycle time 4.81
Buffer 4 Objects leaving 0.00
Final inventory 41.27
Minimum inventory 0.00
Maximum inventory 41.27
Mean inventory 19.36
Mean cycle time Infinite
Decision Point(s) Decision Point 1 Objects leaving 44.55
Final inventory (int. buff.) 0.00
Mean inventory (int. buff.) 0.00
Mean cycle time (int. buff.) 0.00
Resource(s)
Ticket Clerk Mean number in use 0.25
Peter Mean number in use 0.69
Sharon Mean number in use 0.68
Part 2 (a)
Overall Waiting time= The sum of Weighted Mean cycle time at Buffers

Overall Waiting Time= (0.21*100%)+ (6.85*42.5%)+(4.82*57.5%)
Overall Waiting Time= 0.21+2.911+2.77
Overall Waiting Time=5.8925 minutes
Part 2 (b)
Total Number of Customers served during the 3 hours peak
Final inventory of Buffer=total customers
Hence=41.27 customers
Part 2 (c)
The result is given by objects leaving Buffer 1
hence, 44.81 customers
Part 2 (d)
Utilization of the three employees
Ticket Clerk=0.25 or 25%
Peter =0.69 or 69%
Sharon=0.68 or 68%
Part 3
We can employee Mary to hand individuals who want both registration and licensing services
from the officers.
Hence, we will add the following elements
 Buffer 5
 Work Station 4

Flowchart
Customer Arrival
Queues in Line for Ticket Buffer 1
Decision
Point 1
Licensing With Sharon
Work station 3
Registration with Peter
Work station 2
Clerk Issues Ticket
Work station 1
Customer Exit
Buffer 5
45%
25%
30%
Licensing Waiting
Buffer 3
Registration Waiting
Buffer 2
Both Waiting Buffer 4
Both With Mary Work Station 4

Simulation results
Simulation Results (500)
Element Element Statistics Overall
types names Means
Entrance(s) Customer Arrivals Objects entering process 45.09
Objects unable to enter 0.00
Service level 1.00
Work Station(s) Work Station 1 Final status NA
Final inventory (int. buff.) 0.00
Mean inventory (int. buff.) 0.00
Mean cycle time (int. buff.) 0.00
Work cycles started 45.04
Fraction time working 0.25
Fraction time blocked 0.00
Work Station 2 Final status NA
Final inventory (int. buff.) 0.00
Mean inventory (int. buff.) 0.00
Mean cycle time (int. buff.) 0.00
Work cycles started 13.15
Fraction time working 0.50
Fraction time blocked 0.00
Work Station 3 Final status NA
Final inventory (int. buff.) 0.00
Mean inventory (int. buff.) 0.00
Mean cycle time (int. buff.) 0.00
Work cycles started 19.69
Fraction time working 0.54
Fraction time blocked 0.00
Work Station 4 Final status NA
Final inventory (int. buff.) 0.00
Mean inventory (int. buff.) 0.00
Mean cycle time (int. buff.) 0.00
Work cycles started 11.19
Fraction time working 0.29
Fraction time blocked 0.00
Buffer(s) Buffer 1 Objects leaving 45.04
Final inventory 0.04
Minimum inventory 0.00
Maximum inventory 1.93
Mean inventory 0.05
Mean cycle time 0.20
Buffer 2 Objects leaving 13.15
Final inventory 0.32
Minimum inventory 0.00
Maximum inventory 2.06
Mean inventory 0.27
Mean cycle time 3.18
Buffer 3 Objects leaving 19.69
Final inventory 0.40
Minimum inventory 0.00
Maximum inventory 2.49
Mean inventory 0.32
Mean cycle time 2.66
Buffer 4 Objects leaving 11.19
Final inventory 0.08
Minimum inventory 0.00
Maximum inventory 1.30
Mean inventory 0.07
Mean cycle time 0.95
Buffer 5 Objects leaving 0.00
Final inventory 42.58
Minimum inventory 0.00
Maximum inventory 42.58
Mean inventory 20.23
Mean cycle time Infinite
Decision Point(s) Decision Point 1 Objects leaving 44.82
Final inventory (int. buff.) 0.00
Mean inventory (int. buff.) 0.00
Mean cycle time (int. buff.) 0.00
Resource(s)
Ticket Clerk Mean number in use 0.25
Peter Mean number in use 0.50
Sharon Mean number in use 0.54
Mary Mean number in use 0.29

Overall Waiting time = (0.20*100%)+(3.18*30%)+(2.66*45%)+(0.95*25%)
Overall Waiting time=2.59 minutes
Waiting time reduced by 5.8925-2.59=3.3025 minutes
Total Customers Served=42.58 customers
Increase in number of customers served 42.58-41.27= 1.31 customers
Seen by Clerk but waiting to be served=45.04 customer
Increased by 45.04- 44.81=0.23 customers
Utilization of all four employees
Ticket Clerk=0.25 or 25%
Peter =0.50 or 50%
Sharon=0.54 or 54%
Mary=0.29 or 29%
Old Values
Peter =0.69 or 69%
Sharon=0.68 or 68%
Reduced Peter and Sharon's utilization by 19% and 14% respectively
Part 4

If management decides to employee Mary it would be ideal for her to be assigned to the counter
that handles individuals that are looking for both registration and licensing service. This will
reduce the workload assigned to Peter and Sharon thereby giving them the optimal opportunity to
aid clients. But her efforts would be most utilized at the ticket counter as a means of reducing
customer delay and time wastage at this station.
Question 5
Part 1
Specify algebraically the complete second order model for the data.
The second order model for the data is as follows.
Y = β0 + β1 x1 +β2 x2 + β3 x12+β4 x22+ β5 x1x2 + ε
Where,
x = independent explanatory variable and
y = dependant response variable
x1 = Temperature (F0)
x2 = Pressure (Psi)
B0 = estimated mean value of y when x is 0 (y intercept)
Bi = change in mean value of y for unit change in x (gradient of best fit)
For our current situation, the model is for all values of quality(y) is as follows:
52.8 = β0 + 200β1 +50β2 + 40,000β3 + 2,500β4+ 10,000β5 + ε
58.7 = β0 + 200β1 +50β2 + 40,000β3 + 2,500β4 + 10,000β5 + ε
55.4 = β0 + 200β1 +50β2 + 40,000β3 + 2,500β4 + 10,000β5 + ε
63.4 = β0 + 250β1 +50β2 + 62,500β3+ 2,500β4+ 12,500β5 + ε
61.6 = β0 + 250β1 +50β2 + 62,500β3 + 2,500β4+ 12,500β5 + ε

63.4 = β0 + 250β1 +50β2 + 62,500β3 + 2,500β4+ 12,500β5 + ε
46.6 = β0 + 300β1 +50β2 + 90,000β3 + 2,500β4+ 15,000β5 + ε
49.1 = β0 + 300β1 +50β2 + 90,000β3 + 2,500β4+ 15,000β5 + ε
46.4 = β0 + 300β1 +50β2 + 90,000β3 + 2,500β4+ 15,000β5 + ε
92.4 = β0 + 200β1 +60β2 + 40,000β3 + 3,600β4 + 12,000β5 + ε
90.9 = β0 + 200β1 +60β2 + 40,000β3 + 3,600β4 + 12,000β5 + ε
90.9 = β0 + 200β1 +60β2 + 40,000β3 + 3,600β4 + 12,000β5 + ε
93.8 = β0 + 250β1 +60β2 + 62,500β3 + 3,600β4+ 15,000β5 + ε
92.1 = β0 + 250β1 +60β2 + 62,500β3 + 3,600β4+ 15,000β5 + ε
97.4 = β0 + 250β1 +60β2 + 62,500β3 + 3,600β4+ 15,000β5 + ε
69.8 = β0 + 300β1 +60β2 + 90,000β3 + 3,600β4+ 18,000β5 + ε
72.5 = β0 + 300β1 +60β2 + 90,000β3 + 3,600β4+ 18,000β5 + ε
73.2 = β0 + 300β1 +60β2 + 90,000β3 + 3,600β4+ 18,000β5 + ε
74.5 = β0 + 200β1 +70β2 + 40,000β3 + 4,900β4 + 14,000β5 + ε
73.0 = β0 + 200β1 +70β2 + 40,000β3 + 4,900β4 + 14,000β5 + ε
71.2 = β0 + 200β1 +70β2 + 40,000β3 + 4,900β4 + 14,000β5 + ε
70.9 = β0 + 250β1 +70β2 + 62,500β3 + 4,900β4+ 17,500β5 + ε
68.8 = β0 + 250β1 +70β2 + 62,500β3 + 4,900β4+ 17,500β5 + ε
71.3 = β0 + 250β1 +70β2 + 62,500β3 + 4,900β4+ 17,500β5 + ε
38.7 = β0 + 300β1 +70β2 + 90,000β3 + 3,600β4+ 21,000β5 + ε
42.5= β0 + 300β1 +70β2 + 90,000β3 + 3,600β4+ 21,000β5 + ε
41.4 = β0 + 300β1 +70β2 + 90,000β3 + 3,600β4+ 21,000β5 + ε

For our current situation, the model is for all values of quality(y) is as follows:
Part 2
The best fit model is given by
The Model is significant and the adjusted r-squared predicts that 98% of the change in the
dependent variable can be explained by the independent variable.
Part 3

The graphs are considerably similar in shape and general distribution of data point. This can be
proved through the analysis of means and one way analysis of quality for both variables
temperature and pressure. By trying to create a cubic function the information from the graph
appears disjointed and fails to cover all points. Moreover, it does not satisfy the linear equation
y=B0+B1x1+B2x2+e
Therefore, we stick with the linear model since the data cannot be represented in a cubic manner.
Hence, a line of best fit is recommended. (Charts in excel document)
Part 4
Hence, the most efficient value to use would ne Temperature 200⁰F and Pressure of 50 Psi the
values of these two is the only one that is most significant at alpha 0.05 at their respective and
combined t statistics.