SIT192 Discrete Mathematics Assignment 3: RSA Encryption
VerifiedAdded on 2022/11/23
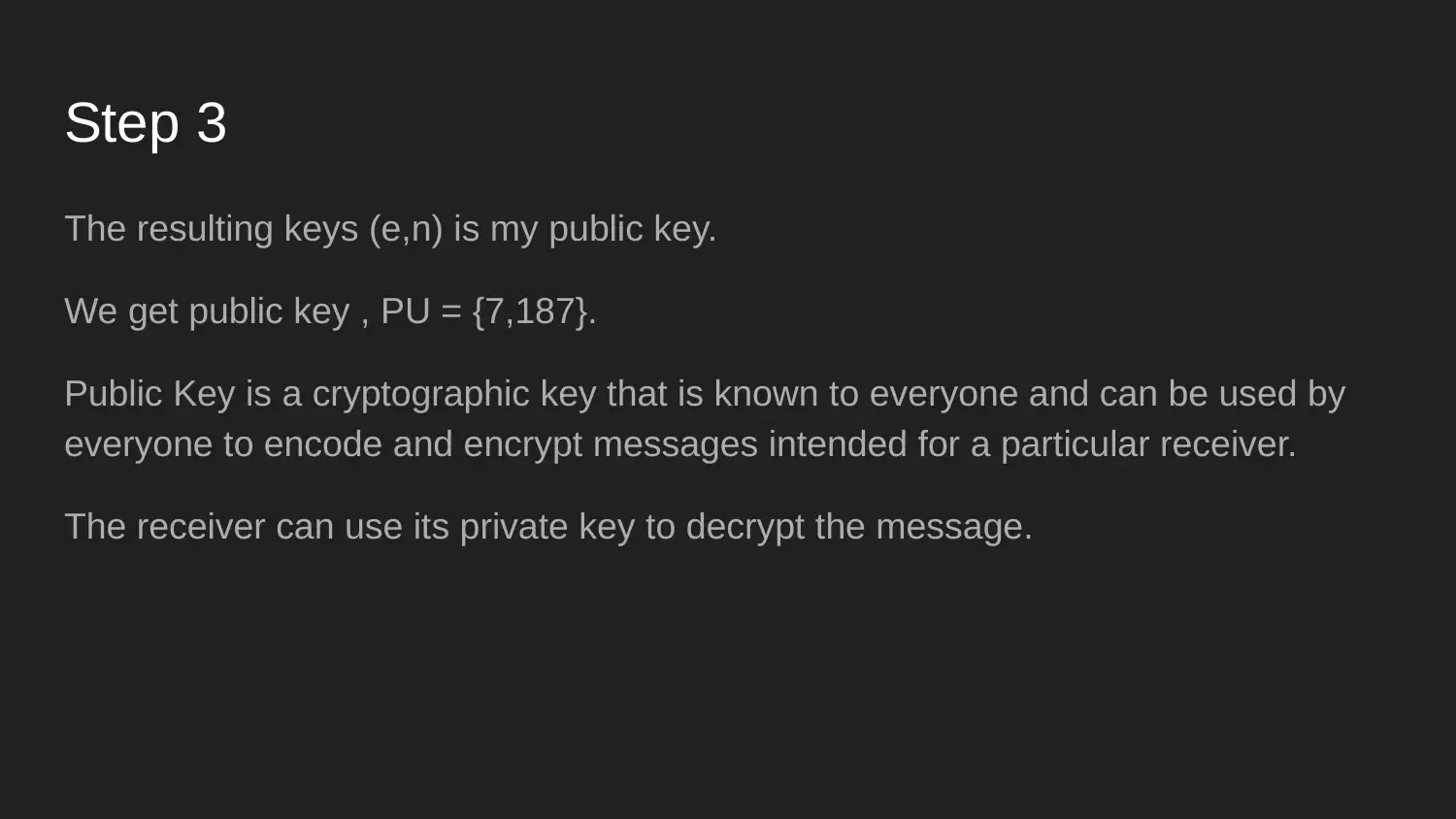
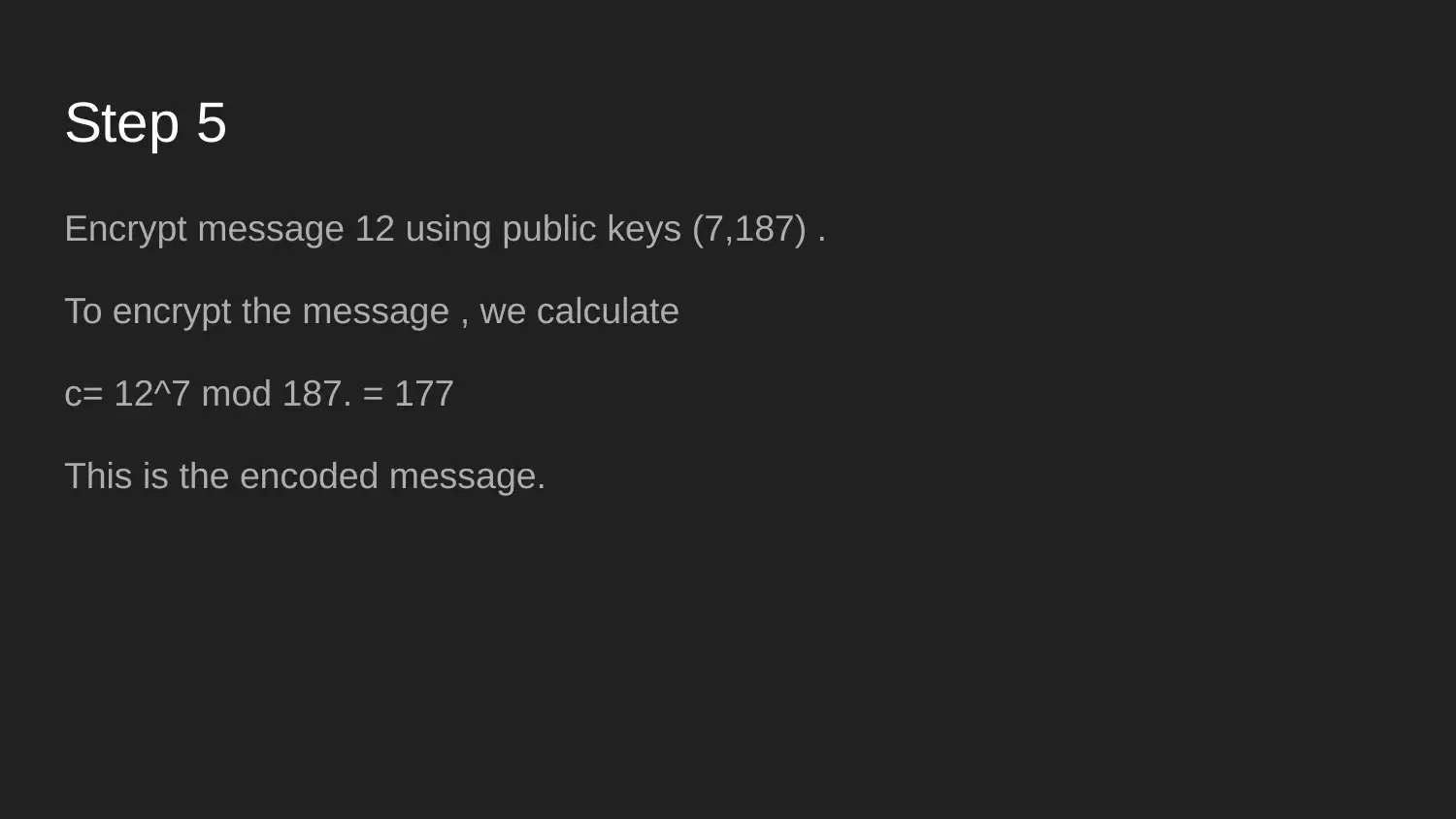
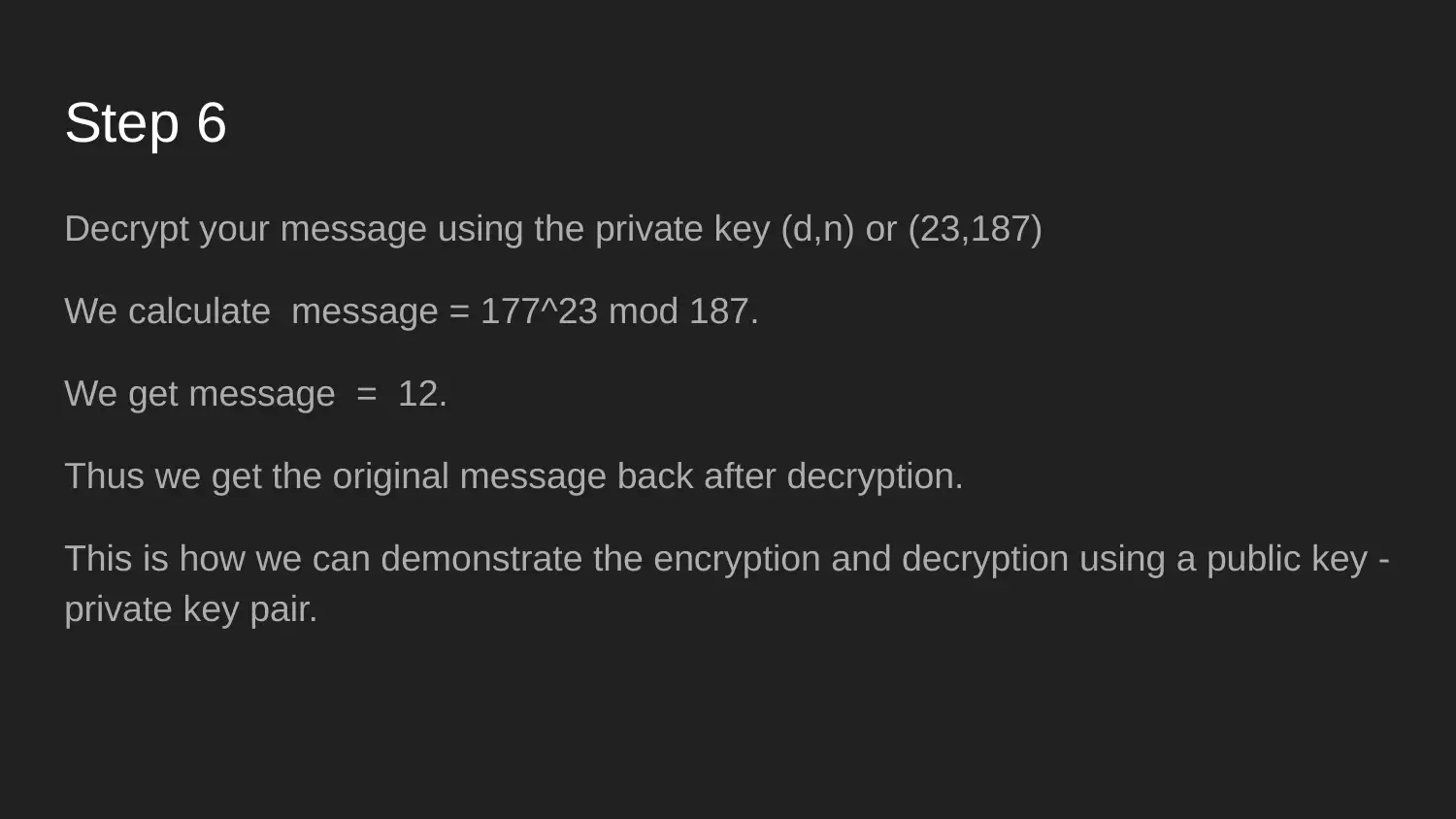
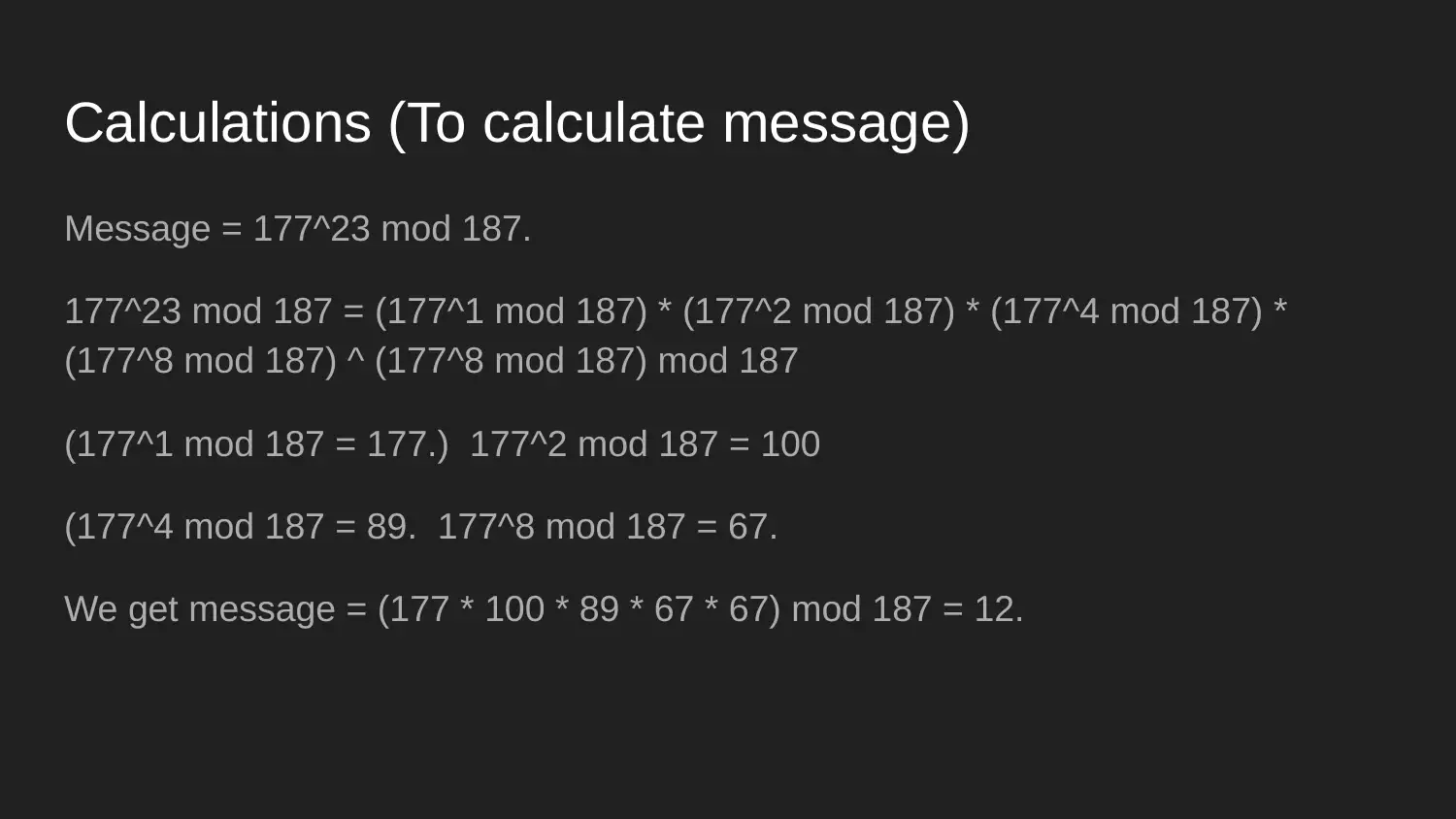
|10
|555
|325
Presentation
AI Summary
This presentation explains the RSA encryption algorithm, a fundamental concept in public-key cryptography. The assignment demonstrates the RSA algorithm through a step-by-step example. It begins by selecting two prime numbers, p and q, to calculate n and m. It then explains the selection of a public key exponent, e, and the calculation of the private key exponent, d. The core of the presentation involves encrypting a message using the public key and decrypting it using the private key, showcasing the mathematical operations involved, including modular exponentiation. The calculations are presented in detail, illustrating how the original message is recovered after decryption, effectively demonstrating the encryption and decryption process using a public-private key pair. This assignment is part of the SIT192 Discrete Mathematics course at Deakin University, focusing on the student's ability to explain mathematical concepts in an oral presentation.
1 out of 10













![[object Object]](/_next/static/media/star-bottom.7253800d.svg)