Slope Stability Analysis for an Existing Railway Embankment

This report discusses the stability analysis of an existing railway embankment using limit equilibrium method and Bishop’s simplified method. It also covers the adjustments made to achieve a minimum factor of safety of 1 for each section of the embankment. The report highlights the significance of cohesion and groundwater level in determining the stability of the embankment.

Slope Stability Analysis 1
SLOPE STABILITY ANALYSIS
Name
Course
Professor
University
City/state
Date

Slope Stability Analysis 2
Slope Stability Analysis
Part A
Introduction
The purpose of this report is to carry out a stability analysis for an existing railway
embankment which has been in place for just over 80 years. The total length of the embankment
is 500 metres, which is divided to 5 separate sections. The entire section has been assessed for
stability. Soil strength parameters have been derived for each embankment section by carrying
out an intrusive ground investigation using window sampling.
Typically, the strength of the drained case is higher than the strength of undrained case.
But in case of low normal stresses, the strength of the drained case tends to be a lot lower
compared with when normal stresses are high.
Methodology
Stability analysis for the existing embankment has been evaluated using limit equilibrium
method and it has been performed using oasys slope 19.1 software according to Bishop’s
simplified method. The assumption made by this method is that the slip surface is circular and
the forces on the sides of the slices are horizontal (no shear). The stratum coordinates and the
ground water coordinates have been calculated for the 5 sections of the railway embankment
separately using soil strength parameters. The obtained data has been applied in the software for
drained and undrained cases. Drained analysis represent the long term condition when the
embankment without the train whilst undrained analysis represents the short term condition when
the embankment subjected to train’s load. The undrained loading analyses have been performed
using total stress parameters (Cu, φ) while the drained analyses (unloading) were performed by

Slope Stability Analysis 3
applying the effective stress parameters (C', φ'). The input of slip surface data including centres
on grid about local axis (spacing) has been adjusted by trial and error procedures in order to get a
minimum factor of safety ensuring that the critical point is within the grid and the grid is in a
reasonable position.
Results
Th results obtained from the two analyses are presented in Table 1 and 2 below.
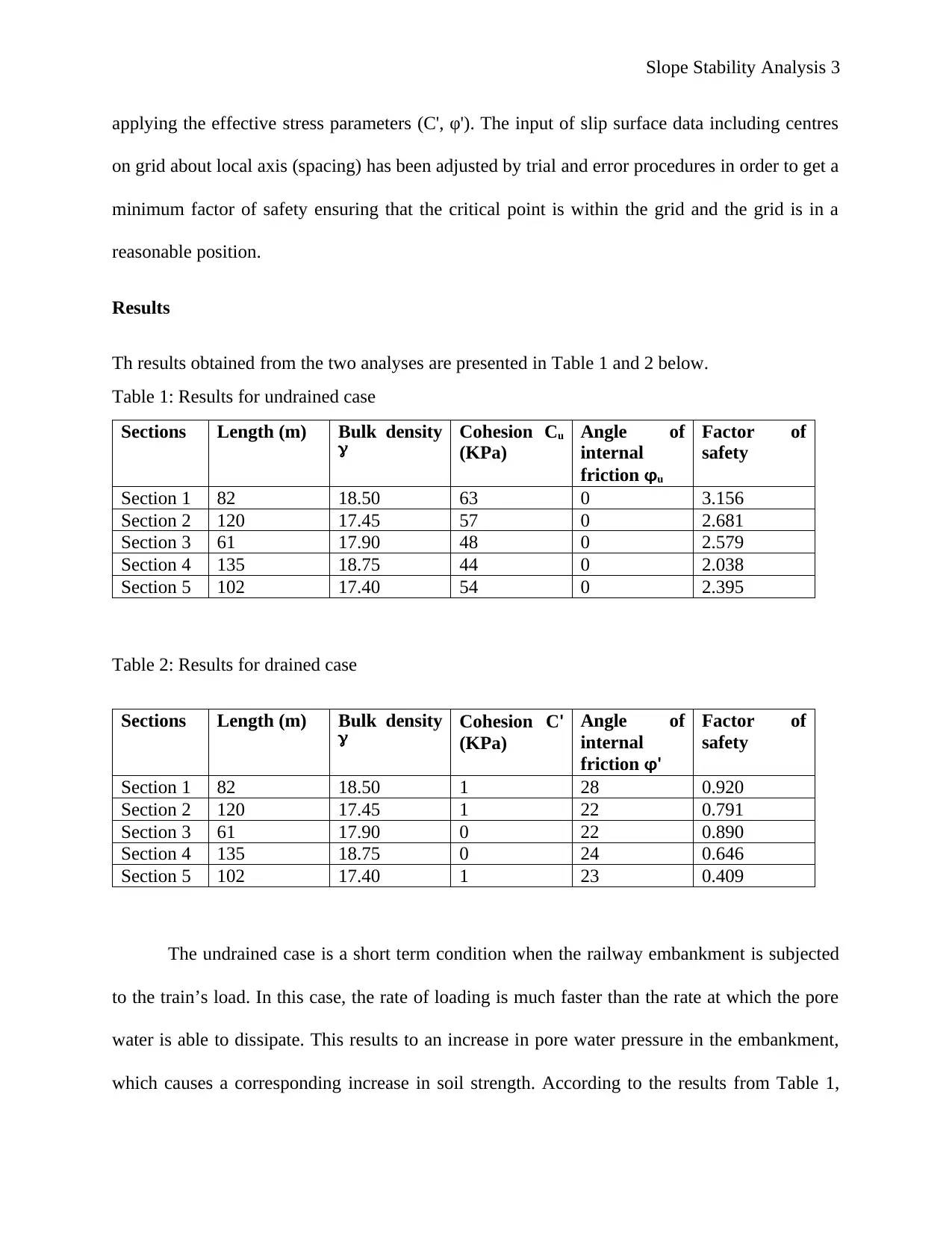
Table 1: Results for undrained case
Sections Length (m) Bulk density
 Cohesion Cu
(KPa)
Angle of
internal
friction φu
Factor of
safety
Section 1 82 18.50 63 0 3.156
Section 2 120 17.45 57 0 2.681
Section 3 61 17.90 48 0 2.579
Section 4 135 18.75 44 0 2.038
Section 5 102 17.40 54 0 2.395
Table 2: Results for drained case
Sections Length (m) Bulk density
 Cohesion C'
(KPa)
Angle of
internal
friction φ'
Factor of
safety
Section 1 82 18.50 1 28 0.920
Section 2 120 17.45 1 22 0.791
Section 3 61 17.90 0 22 0.890
Section 4 135 18.75 0 24 0.646
Section 5 102 17.40 1 23 0.409
The undrained case is a short term condition when the railway embankment is subjected
to the train’s load. In this case, the rate of loading is much faster than the rate at which the pore
water is able to dissipate. This results to an increase in pore water pressure in the embankment,
which causes a corresponding increase in soil strength. According to the results from Table 1,

Slope Stability Analysis 4
undrained case shows that the embankment is stable as the FOS values are more than 1 for all
sections. A section with higher cohesion value results in a higher FOS. Section 1 shows the
highest FOS due to the highest cohesion value 63.
In the undrained case, the angle of internal friction (φu) was zero meaning that there was
no frictional component in determining the shear stress at failure. Therefore shear stress at failure
was mainly dependent on the cohesive component. As a result, the higher the cohesion the
greater the FOS. The cohesion values of the soil and the groundwater level in the undrained case
were high enough for the embankment to be stable hence there was no need for adjustments.
Drained is a long term condition when the power water pressure has dissipated meaning
that there is no change in power water pressure. In this scenario, the shear strength of the soil is
lower than the applied load (shear stress) therefore the embankment is unstable with FOS of less
than 1 for all sections. This behavior or condition of soil is exhibited by higher friction angles
and a lower cohesion values. The lower cohesion values means very low shear stress at failure
because shear stress at failure is largely dependent on cohesion and slightly dependent on
internal angle of friction. When shear stress at failure is small, it means that the embankment has
lower capability of withstanding the load or stress applied on it and therefore it is likely to fail. In
fact, a FOS of less than 1 means that the embankment will fail because it cannot support the
minimum allowable stress.
PART B
The results for drained analysis doesn’t reflect the actual conditions of the embankment
as it shows that the embankment is unstable for all 5 sections. This is because the FOS for all the
sections of the embankment is less than 1, as shown in Table 2 above. If this was the case, the

Slope Stability Analysis 5
embankment would have failed immediately any load was applied on it. When a FOS is less than
one, it means that the structure cannot support the minimum allowable load or stress according to
its design specifications. This cannot be allowed in any design work because the component or
structure will have been designed to fail. Therefore it was important to make adjustments for soil
strength parameters so as to achieve a minimum FOS of 1. Based on the Mohr-Coulomb failure
criterion, values of angle of internal friction and density of the soil have limited effect on FOS
results whilst cohesion and ground water level have a significant impact on the FOS results.
Cohesion is the most unreliable variable and it is significantly underestimating the actual
strength for the long term condition. Furthermore, adjustments have been done to ground water
level in order to achieve a minimum FOS of 1.
Trees have a significant effect on groundwater level. In most cases, trees lower the
groundwater level by absorbing more water thus reducing the pore pressure in the soil. When the
pore pressure reduces, it means that the soil becomes less cohesive. The more the soil becomes
less cohesive the more the embankment becomes unstable. Therefore the most appropriate
strategy to make the embankment more stable is to increase the cohesion of the soil i.e. the
cohesive component, disregarding the frictional component due to its insignificant impact on the
overall stability of the embankment. This also helps in reducing the minimum weight of the
section of the embankment that is mostly affected by the lower groundwater level due to
presence of trees.
Adjustments
As stated above, adjustments were made to the cohesion and groundwater level for the drained
case so as to achieve a minimum FOS of 1 for each section of the embankment. The adjustments
made and the new FOS are provided in Table 3 below

Slope Stability Analysis 6
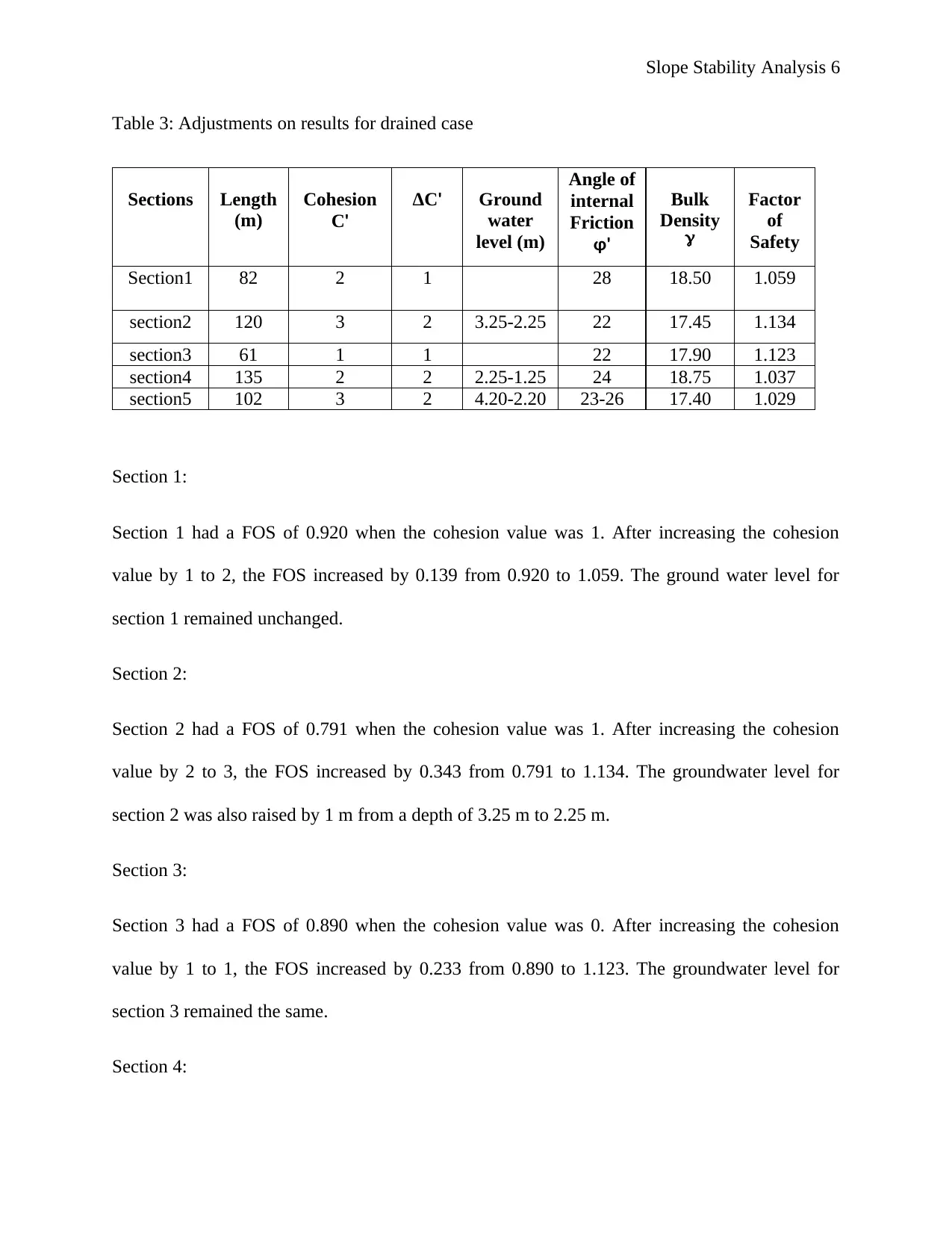
Table 3: Adjustments on results for drained case
Sections Length
(m)
Cohesion
C'
ΔC' Ground
water
level (m)
Angle of
internal
Friction
φ'
Bulk
Density

Factor
of
Safety
Section1 82 2 1 28 18.50 1.059
section2 120 3 2 3.25-2.25 22 17.45 1.134
section3 61 1 1 22 17.90 1.123
section4 135 2 2 2.25-1.25 24 18.75 1.037
section5 102 3 2 4.20-2.20 23-26 17.40 1.029
Section 1:
Section 1 had a FOS of 0.920 when the cohesion value was 1. After increasing the cohesion
value by 1 to 2, the FOS increased by 0.139 from 0.920 to 1.059. The ground water level for
section 1 remained unchanged.
Section 2:
Section 2 had a FOS of 0.791 when the cohesion value was 1. After increasing the cohesion
value by 2 to 3, the FOS increased by 0.343 from 0.791 to 1.134. The groundwater level for
section 2 was also raised by 1 m from a depth of 3.25 m to 2.25 m.
Section 3:
Section 3 had a FOS of 0.890 when the cohesion value was 0. After increasing the cohesion
value by 1 to 1, the FOS increased by 0.233 from 0.890 to 1.123. The groundwater level for
section 3 remained the same.
Section 4:

Slope Stability Analysis 7
Section 4 had a FOS of 0.646 when the cohesion value was 0. After increasing the cohesion
value by 2 to 2, the FOS increased by 0.391 from 0.646 to 1.037. The groundwater level for
section 4 was also raised by 1 m from a depth of 2.25 m to 1.25 m.
Section 5:
Section 5 had a FOS of 0.409 when the cohesion value was 1. After increasing the cohesion
value by 2 to 3, the FOS increased by 0.620 from 0.409 to 1.029. The groundwater level for
section 5 was also raised by 2 m from a depth of 4.20 m to 2.20 m.
It was assumed that the angle of internal friction and bulk density for each of the sections
remained the same. This is a very conservative assumption because typically, a change in
groundwater level is likely to cause a change in bulk density and internal friction of the soil. This
is due to change in moisture content and void ratio of the soil.
Analysis
The values of cohesion for the drained case were very small and this shows the high level
of inaccuracy in these results. Inasmuch as the drained soil was expected to have lower cohesion
values, the data obtained from the analyses was very small. This is because the small cohesion
values provided FOS of less than 1, which cannot be the case because the value of FOS at any
section of the embankment must be at least 1 or else the embankment would have failed if any
train load was applied to it. It is worth noting that the embankment in this report has been
inexistence for over eight decades.
When an external load is applied on the embankment, the pore water pressure changes.
This is because the load causes water to dissipate from the soil and the groundwater level
changes resulting to changes in effective stress and total stress. The changes in effective and total

Slope Stability Analysis 8
stresses is due to change in power water pressure. This change in pore water pressure is affected
by the groundwater level. Therefore raising the groundwater level increases the power water
pressure in the soil thus making the embankment more stable.
There are also several factors that affect the time taken for the pore water pressure to
dissipate in the embankment. Some of these include: the amount of pore water pressure that has
to be dissipated (higher amount of pore water pressure will take more time to dissipate than less
amount); the permeability of the soil (the pore water pressure takes shorter time to dissipate in
more permeable soil than is less permeable soil); and the drainage path or the distance that the
pore water pressure has to flow (the pore water pressure takes less time to dissipate over a short
distance than a longer distance).
In undrained case, the frictional component was zero because the angle of internal
friction was zero. This means that the shear strength at failure was dependent on cohesion only.
Since the cohesion values for the undrained case were higher, the FOS values were also greater
than 1 (as show in Table 1) and there was no need for adjustments. For the drained case, the
frictional component was not zero because the angle of internal friction was not zero. However,
the cohesion values were very small resulting to FOS values of less than one. This made it
necessary to adjust the cohesion values and groundwater levels so as to achieve a minimum FOS
of 1 for each section of the embankment.
For the embankment to be stable, it shear strength should be greater than the total stress
applied on it by the train load. This requires the soil to have higher cohesion, higher normal
stress and a relatively higher angle of internal friction. When pore pressure is increased in
undrained loading, the effective stress of the embankment decreases. This is because the
increased pore pressure reduces the cohesion of the soil and also the normal stress of the soil. In

Slope Stability Analysis 9
other words, both the cohesive component and the frictional component of the embankment
decreases thus reducing the effective stress and shear strength of the embankment.
In general, soils are frictional materials whose strength is dependent on the stresses
applied on them. The effective stresses control the strength of the soil. Therefore pore water
pressures are essential because they affect the effective stresses of the soil. The strength of soil
also depends on drainage or permeability. In undrained condition, deformation of the soil takes
place at constant volume while in drained condition, deformation of the soil takes place without
necessarily developing excess pore water pressures.
Moisture content is also a very essential factor affecting strength of soil. In drained
condition, the volume of water in the soil is constant hence there is a slight or no change in
pressure exerted on the soil. This means that the embankment soil is less flexible hence cannot
withstand the load exerted on it by the train. On the other hand, undrained soil condition is more
flexible because when the train load is applied on the embankment, the water pressure in the soil
increases thus increasing the capability of the embankment to withstand the load applied on it.
Summary
Undrained case
 FOS greater than 1 at all sections: the soil strength is greater than the applied load (stress)
of the train, therefore the embankment is stable
 The FOS was higher due to higher cohesion value
 Undrained is a short term loading condition when the embankment is subjected to the
train load.

Slope Stability Analysis 10
 FOS-Total stress- undrained condition, the rate of loading is much quicker than the rate at
which the pore water is able to drain out of the soil.
Drained case
 FOS less than 1 t all sections: the soil strength is less than the applied load (stress) of the
train, therefore the embankment is unstable.
 The FOS was smaller due to lower cohesion value
 Drained is a long term loading condition when the embankment is not subjected to the
train load.
 FOS-Total stress- drained condition, the rate of loading is much slower than the rate at
which the pore water is able to drain out of the soil.