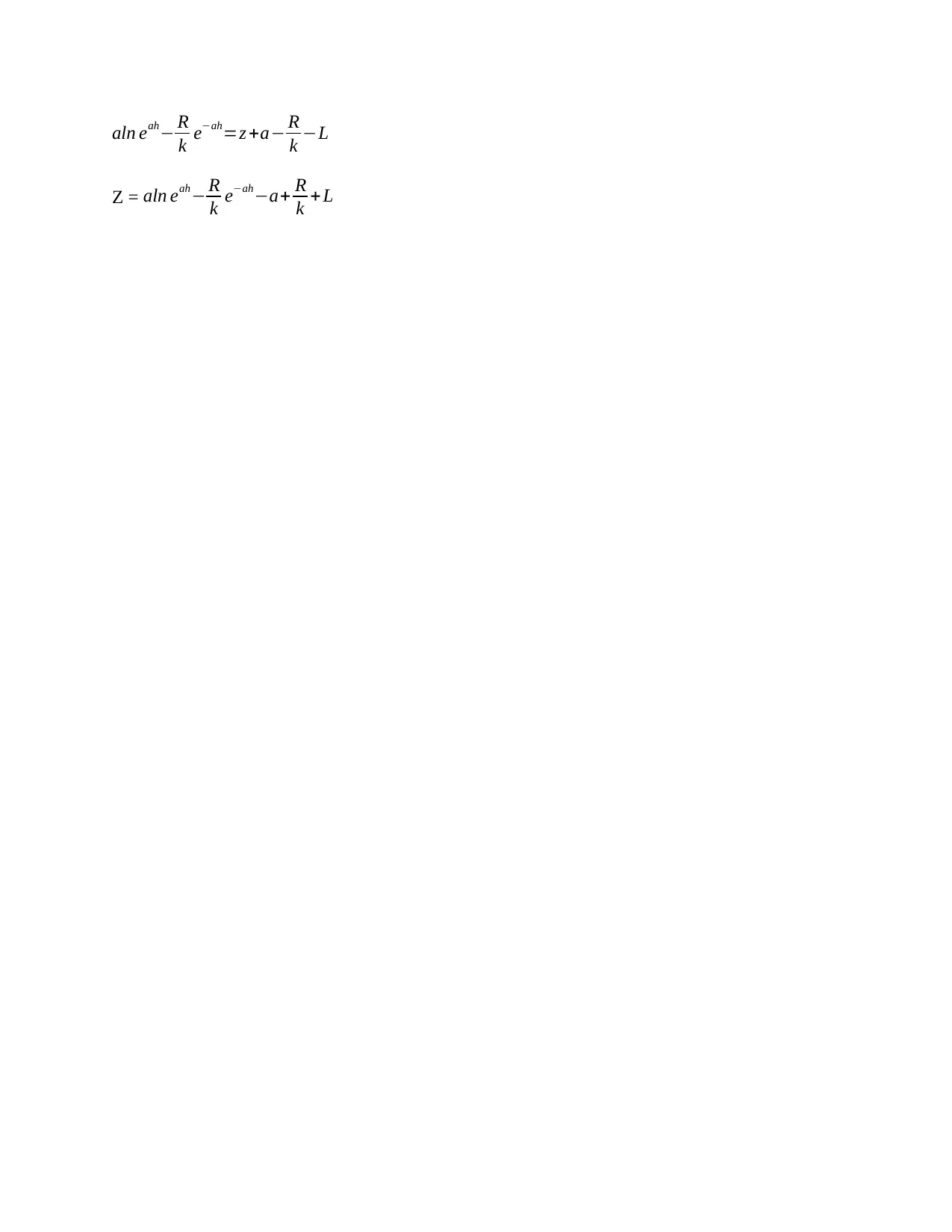MAT1CDE Assignment 4: Differential Equations and Applications, 2018
VerifiedAdded on 2023/06/03
|10
|1044
|377
Homework Assignment
AI Summary
This document contains solutions to several differential equations problems, likely part of the MAT1CDE Assignment 4. The problems cover topics such as separable differential equations, finding particular solutions given initial conditions, and applications involving steady flow and hydraulic conductivity. Various integration techniques are applied to solve these equations, and the solutions are presented with detailed steps. The solutions also include determination of integration constants and domains. One problem involves determining exponential and constant values. This resource is valuable for students seeking assistance with differential equations and related mathematical concepts.
1 out of 10