Optimization, Translation, and Probability in Solar Thermal Power Generation

This report covers the optimization of tower CSP plants, numerical integration of DNI data, and Gaussian probability distribution of MGA diameters. It discusses the trade-offs in determining the operating temperature of the plant, the total conversion efficiency from sunlight to electricity, and the thickness of the aluminum carbide coating. The report also includes MATLAB implementation and results.

Student name
Student ID Number
Date of Submission
1

PROBLEM I: OPTIMIZATION
INTRODUCTION
The solar thermal power is a method of producing electricity by using mirrors to focus sunlight
on a central tower, creating heat, and using that heat to drive a steam power cycle. There are a
number of real problems that surround the solar thermal power generation. The joint WB/GEF
support for two hybrid integrated solar combined cycle plants are deployed in desert countries
such as Abu Dhabi, Morocco, and Egypt. The CSP plants have 20MWatt components. They
provide Global CSP programs that are TF funded so as to bridge the barrier of CSP deployment.
The CTF Regional Investment Plan for CSP in MENA region aims to support the deployment of
a larger power plant. There is an increasing utility interest in deployment of CSP plants to meet
the requirements of renewable energy sources in the portfolio standards such as the recent
implementation of the solar resource in the South West U.S. The government is providing
investment tax credits and to provide incentives so as to encourage the energy harvesting
industry grow.
2

TRANSLATION
The tower CSP plant has a number of trade-offs. One of the main objectives is to determine the
operating temperature of the plant. The efficiency of the steam cycle is given as the selected
temperature and it is estimated as,
ηsc=0.5− 150
T
On the other side of the tower, the receiver is set to have the same temperature as the steam cycle
and the efficiency is obtained as a function of temperature,
ηrec =1− ( T4 −3004 ) x 3.5 x 10−13
It is observed that there is a decrease in the efficiency of the heliostats with operating
temperature increasing. To reduce the high operating temperatures, it is required that more
3

mirrors be stationed further from the tower. The efficiency of the heliostat fields is obtained as a
function of the operating temperature as,
ηfield=1− √ T
40
METHODOLOGY
Data optimization is performed on the three data sets using any of the three main algorithms
under the fsolve function. When the objective function at the initial point x0 is a real, finite
value, pattern search treats polls point failures as if the objective function values are large, and
ignores them and contracts. Whenever the pattern search finds a point that is more feasible than
any previously seen, it will automatically count the element as a successful poll and expand. This
behavior allows for intelligent traversal of the space, and a large class of algorithms has been
developed around this basic idea. The system analyses a non-linear system solver,
• Trust region - min {1
2 sT Hs+ sT g such that ||Ds||≤ Δ }
• Trust region dogleg - J ( xk ) dk=−F ( xk ) , xk+1= xk + dk
• Levenberg-Marquardt - ( J ( xk )T J ( xk ) + λk I ) dk=−J ( xk )T F ( xk )
Set up an initial guess.
RESULTS & DISCUSSION
The optimal temperature required for the system plant to operate is 1600 Kelvin.
The total conversion efficiency from the sunlight to electricity is given as,
4

ηtotal =ηfield∗ηrec∗ηsc
The conversion efficiency is optimized to determine the operating temperature given using the
fsolve() function.
APPENDIX
%% PROBLEM I
... optimization
n_sc=@(T) 0.5-150*T; % efficiency of the steam cycle as a function
% of the selected temperature T (in Kelvin)
n_rec=@(T) (1-(T^4-300^4)*3.5*10^-13); % receiver efficiency with the same
temperature
% as the steam cycle
n_field=@(T) 1-(sqrt(T)/40); % efficiency of the heliostat field
n_field as a
% function of the operating temperature
% of the plant T.
n_total=@(T) n_sc(T).*n_rec(T).*n_field(T);
nf_ttl=@(T) n_total(T);
x0=27.3e2;
r=fsolve(nf_ttl,x0) % solves for the non-linear equations
PROBLEM II: NUMERICAL INTEGRATION
INTRODUCTION
Solar energy is a renewable source of energy that is being embraced as a result of the rising cost
of fossil fuel and the observed reduced dependence on energy imports. It is less dependent on
extensive grid infrastructure. It is suitable for decentralized deployment as well as it conserves
the environment. There is a Direct Normal Irradiance profile obtained at the Alice Springs on a
5

day in 07/2005. The DNI is used to measure the direct sunlight that falls on the earth’s surface in
watts per square meter. The system can be used to tell how much energy may be obtained from
the Solar Thermal Power Plants. The solar radiation quantities are made based on the available
data sets, interpolations for future predictions as well as the satellite-based estimates or methods.
Other alternatives to the direct normal irradiation are the diffuse horizontal irradiation, DHI, and
the global horizontal irradiation (GHI). The DNI defines the light that arrives directly from the
sun and that falls onto a plane that is normal to the direction of the sun. For its alternatives, the
GHI refers to the light that arrives on a horizontal plane that falls from the sun, sky and the
clouds and the DHI is all the light that arrives from the sky and the clouds but not directly from
the sun.
TRANSLATION
The method imports the DNI.m matlab data file. It contains data collected for a whole year in 5
minutes intervals. It is estimated that the area has mirrors as A=1000000m2 where this alludes to
a small-medium CSP plant. The DNI can inform the methodology by determining the amount of
energy that can be gathered from the solar thermal power plants. It is given by integrating the
DNI with respect to time. The integral is further multiplied by the total collecting area of the
solar field and the overall power plant efficiency. It is possible to obtain the energy,
E=A∗η∗∫
0
t
DNI ( t ) dt
METHODOLOGY
(i) List out the constants such as the area and the overall total efficiency
(ii) Import the DNI.mat file as provided in the Blackboard. It is a column vector.
6

(iii) The file is saved as a text file and the MATLAB commands are implemented to read
the text file.
(iv) The trapezoidal integral function trapz() function on MATLAB to obtain the
numerical integration of the data obtained on the solar thermal processes since
07/2005.
(v) The final stage is used to obtain the energy in watts per square meter.
RESULTS & DISCUSSION
APPENDIX
The MATLAB implementation
%% PROBLEM II
Area=1000000; %square meters
T=13*(24*60)/5; %Duration the data is collected
ntt_B=(50-150./T)*(1-(T.^4-300^4)*3.5*10^-13)*(1-(sqrt(T)/40))
% importing the DNI data from the blackboard
fileID=fopen('DNI.txt','r');
formatspec='%d';
A=fscanf(fileID,formatspec); %Reads the file data and outputs an array filling
A
% performing the numerical integration of the column vector
... using the trapezoidal numerical integration
DNI=trapz(A) % Numerical integral output
% To obtain the energy of the CSP plant
E=Area*ntt_B*DNI;
Energy=E/10e14; %For formatting purposes
fprintf('The Energy of the CSP plant:\n %.3fe15 Watts/m^2\n',Energy)
PROBLEM III: PROBABILITY
7

INTRODUCTION
The Miscibility Gap Alloys are used where there are two immiscible components that are
combined in a microstructure that a high melting temperature material encapsulates a lower
melting temperature metallic phase material. It is considered that the MGAs of the carbon
encapsulating spherical pockets of aluminum and the materials are mixed in equal volumes. The
materials are mixed in equal volumes.
The diameters of the aluminum particles in our sample are distributed by a Gaussian or normal
distribution given the mean of 7mm and a standard deviation of 1.58mm. There is energy lost
when the MGA operating temperature scales too high. This is a result of the reaction between the
aluminum pocket and the surrounding carbon matrix that reduces the size of the aluminum
pocket.
TRANSLATION
The Gaussian probability distribution function is used as the bell shaped curve or the normal
distribution. The Gaussian PDF is a continuous distribution given as,
8
p( y )= 1
σ √ 2 π e
−( y −μ )2
2 σ2

The total area under the curve is normalized to one by the σ√(2π) factor such that,
The measurements are such that they are a number of standard deviations away from the mean of
the Gaussian. As a result, the probability of a given measurement is found to be |
 - n
|.
METHODOLOGY
To determine thickness of the aluminum carbide coating by,
δ=∫
0
t
Rτ dt
(i) List the constants. Note that the gas constant is similar to the Boltzmann’s constant.
(ii) The Gaussian distribution plot mean and standard deviation are defined. The range
used is [-10,15].
RESULTS & DISCUSSION
(i) Plotting the PDF of the diameters of the aluminum particles
9

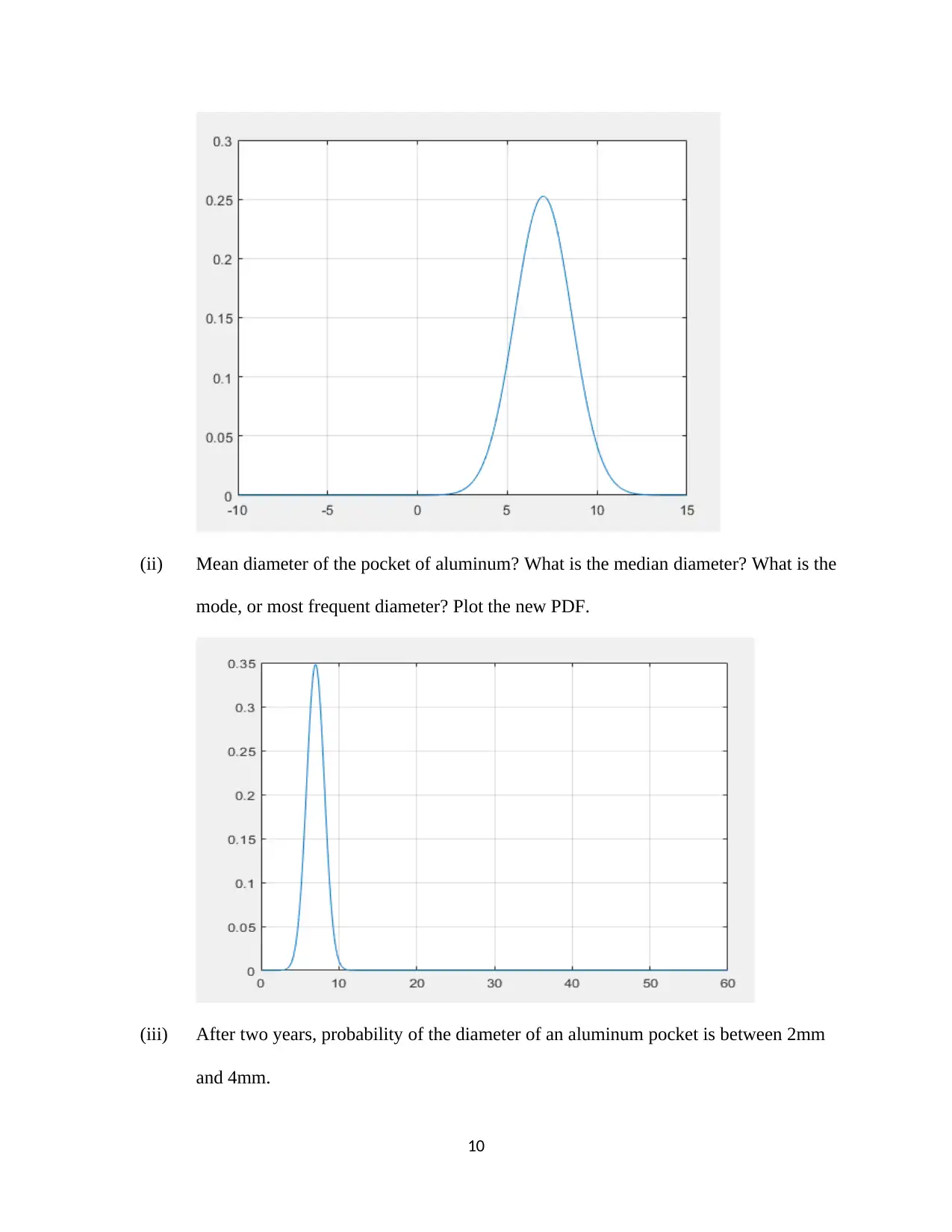
(ii) Mean diameter of the pocket of aluminum? What is the median diameter? What is the
mode, or most frequent diameter? Plot the new PDF.
(iii) After two years, probability of the diameter of an aluminum pocket is between 2mm
and 4mm.
10

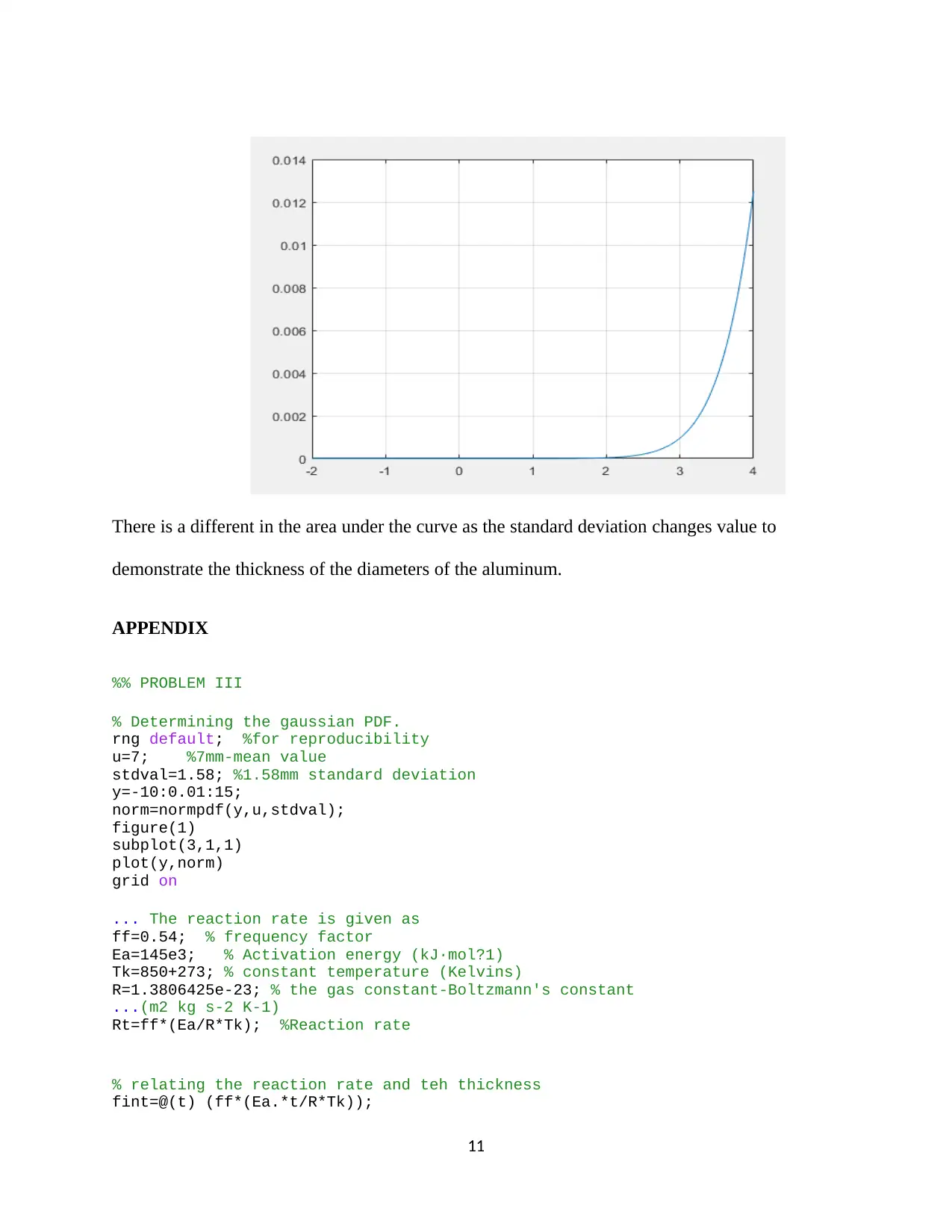
There is a different in the area under the curve as the standard deviation changes value to
demonstrate the thickness of the diameters of the aluminum.
APPENDIX
%% PROBLEM III
% Determining the gaussian PDF.
rng default; %for reproducibility
u=7; %7mm-mean value
stdval=1.58; %1.58mm standard deviation
y=-10:0.01:15;
norm=normpdf(y,u,stdval);
figure(1)
subplot(3,1,1)
plot(y,norm)
grid on
... The reaction rate is given as
ff=0.54; % frequency factor
Ea=145e3; % Activation energy (kJ·mol?1)
Tk=850+273; % constant temperature (Kelvins)
R=1.3806425e-23; % the gas constant-Boltzmann's constant
...(m2 kg s-2 K-1)
Rt=ff*(Ea/R*Tk); %Reaction rate
% relating the reaction rate and teh thickness
fint=@(t) (ff*(Ea.*t/R*Tk));
11

time=60;
tr=0:0.01:time;
dthick=integral(fint,0,time);
%new standard deviation value
d_median=dthick/2 % defines the median
d_mode=Rt/5 %defines the mode
stdval2=dthick/1e34;
subplot(3,1,2)
norm2=normpdf(tr,u,stdval2);
plot(tr,norm2)
grid on
%after two years
tr2=0:0.01:time*2;
stdval3=stdval2*0.145+1;
norm3=normpdf(tr2,u,stdval3);
subplot(3,1,3)
plot(tr2,norm3)
grid on
REFERENCES
[1]. Sugo, H, Kisi, E, Bradley, J, Fiedler, T, & Luzin, V 2017, ’In situ neutron diffraction
studies of operating MGA thermal storage materials’, Renewable Energy And
Environmental Sustainability, Vol 2, P 34 (2017), p. 34, Directory of Open Access
Journals, EBSCOhost.
12