MAT 120 Spring 2019: Comprehensive Review of Functions for Exam 1

This document provides detailed solutions to review problems for MAT 120 Exam 1, focusing on functions, domains, and asymptotes. It includes finding the domains of various functions, evaluating function expressions, and determining composite functions. The solutions cover topics such as rational f...Read More

Solution: 1(f): Given that
Note that domain of a function is the set of input values for which the function is real and
defined.
So will be defined and real if and
Now solve , this gives . Since , so discard .
So, the domain of is the set of all values except and
In interval notation, the domain of is .
Solution: 1(g) Given that
Note that domain of a function is the set of input values for which the function is real and
defined.
So will be defined and real if .
Since this implies that for real .
Hence domain of is
Solution 2(d): Given
So,
Now,
Hence
Solution 2(f): Given .
Now,
Hence,
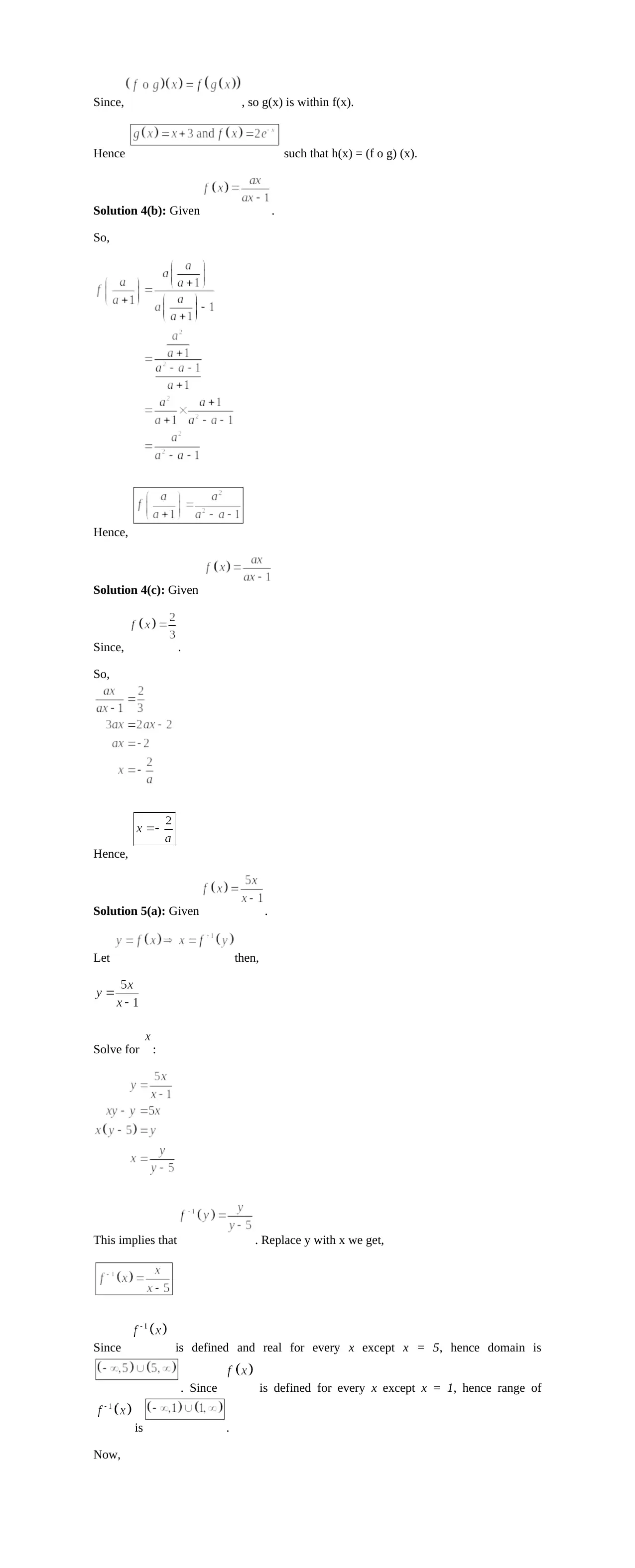
Solution 3(b): Given .
Since, , so g(x) is within f(x).
Hence such that h(x) = (f o g) (x).
Solution 3(d): Given .

Since, , so g(x) is within f(x).
Hence such that h(x) = (f o g) (x).
Solution 4(b): Given .
So,
Hence,
Solution 4(c): Given
Since, .
So,
Hence,
Solution 5(a): Given .
Let then,
Solve for :
This implies that . Replace y with x we get,
Since is defined and real for every x except x = 5, hence domain is
. Since is defined for every x except x = 1, hence range of
is .
Now,

Hence,
Solution 8(a): Given .
The formula for difference quotient is .
Now,
So, the difference quotient is
Hence,
Solution 8(b): Given .
The formula for difference quotient is .
Now,
.
So, the difference quotient is
Hence,
Solution 11(a): Given . Since f(x) passes through the points
So, and
Divide equation (i) by equation (ii) we get,
Substitute the value of b in equation (ii) we get,

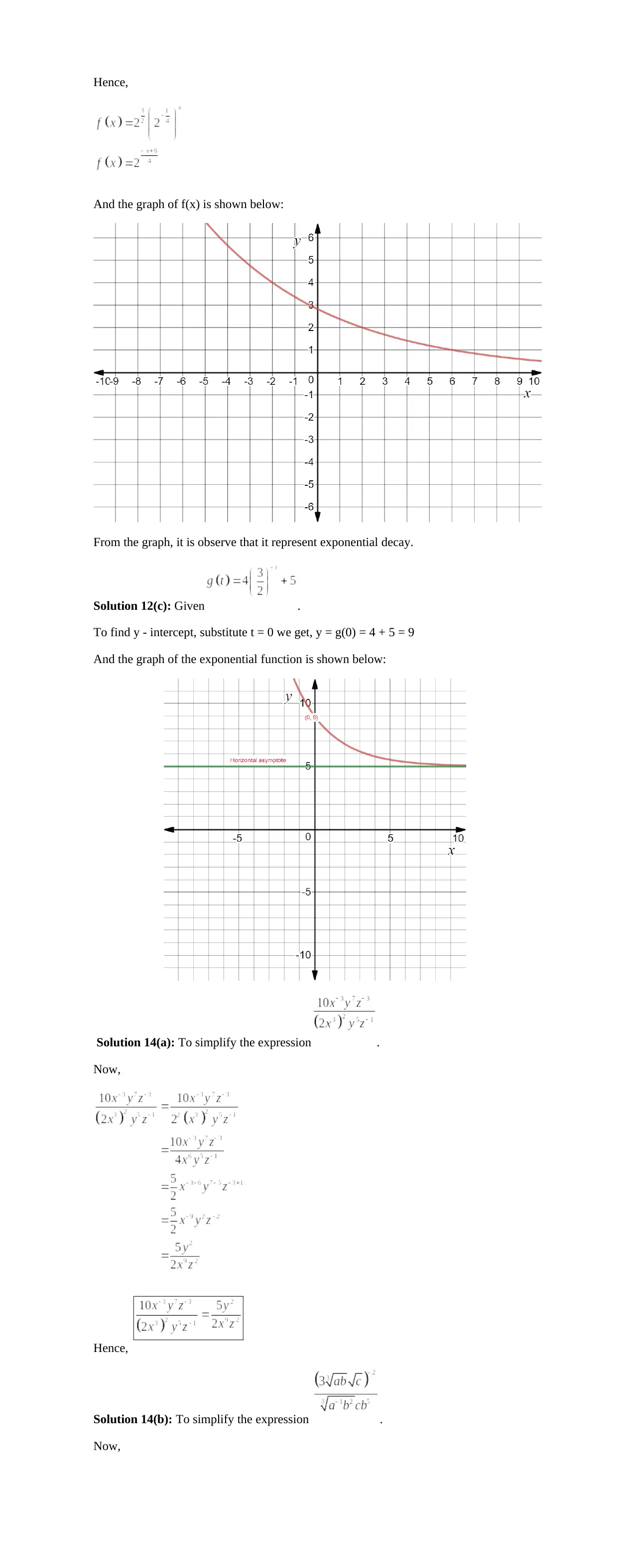
Hence,
And the graph of f(x) is shown below:
From the graph, it is observe that it represent exponential decay.
Solution 12(c): Given .
To find y - intercept, substitute t = 0 we get, y = g(0) = 4 + 5 = 9
And the graph of the exponential function is shown below:
Solution 14(a): To simplify the expression .
Now,
Hence,
Solution 14(b): To simplify the expression .
Now,

Hence,
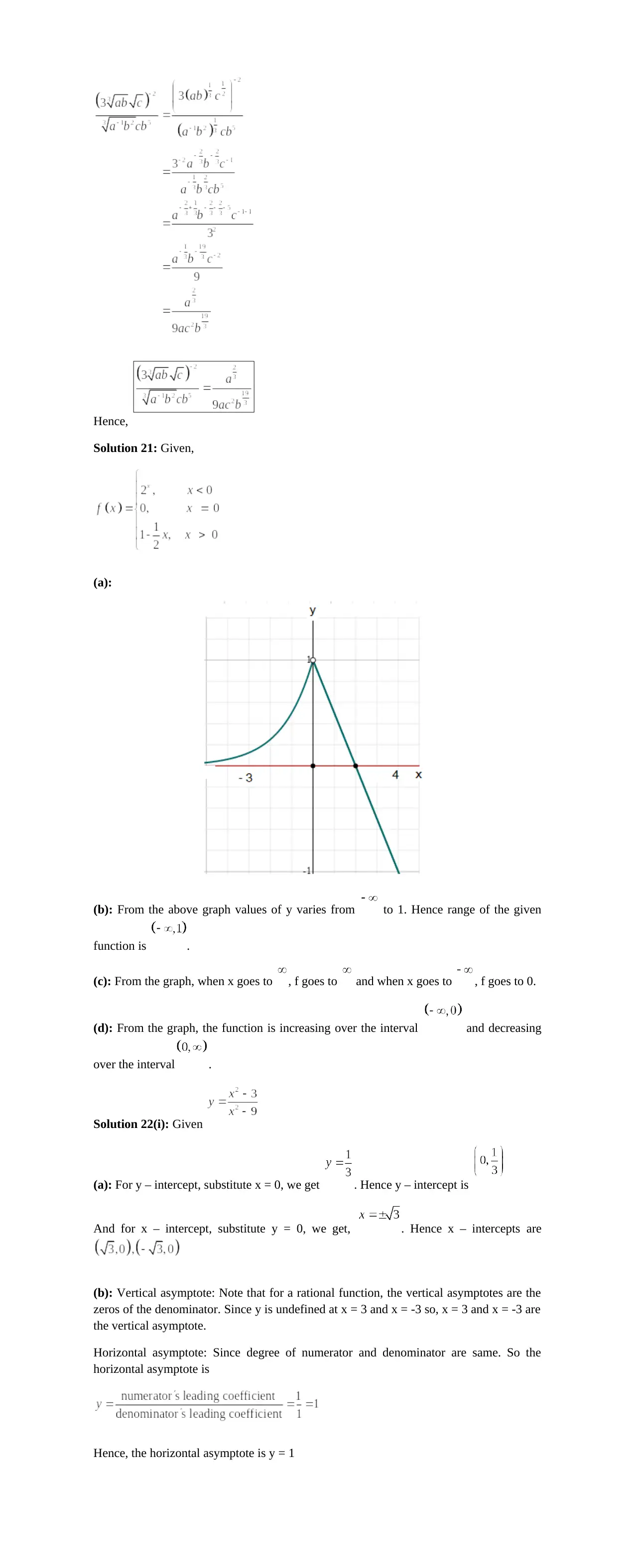
Solution 21: Given,
(a):
(b): From the above graph values of y varies from to 1. Hence range of the given
function is .
(c): From the graph, when x goes to , f goes to and when x goes to , f goes to 0.
(d): From the graph, the function is increasing over the interval and decreasing
over the interval .
Solution 22(i): Given
(a): For y – intercept, substitute x = 0, we get . Hence y – intercept is
And for x – intercept, substitute y = 0, we get, . Hence x – intercepts are
(b): Vertical asymptote: Note that for a rational function, the vertical asymptotes are the
zeros of the denominator. Since y is undefined at x = 3 and x = -3 so, x = 3 and x = -3 are
the vertical asymptote.
Horizontal asymptote: Since degree of numerator and denominator are same. So the
horizontal asymptote is
Hence, the horizontal asymptote is y = 1

Solution 22(ii): Given
(a): For y – intercept, substitute x = 0, we get . Hence y – intercept is
And for x – intercept, substitute y = 0, we get, . Hence x – intercepts are
(b): Vertical asymptote is
Since, numerator degree > 1 + denominator degree. Hence there is not horizontal
asymptote.
Solution 22(iii): Given
(a): For y – intercept, substitute x = 0, we get . Hence y – intercept is
And for x – intercept, substitute y = 0, we get, . Hence x – intercepts are
(b): Vertical asymptote: Note that for a rational function, the vertical asymptotes are the
zeros of the denominator. Since y is undefined at x = -2 and x = 3 so, x = -2 and x = 3 are
the vertical asymptote.
Horizontal asymptote: Since degree of numerator and denominator are same. So the
horizontal asymptote is
Hence, the horizontal asymptote is y = -3
Solution 22(iv): Given
(a): For y – intercept, substitute x = 0, we get . Hence y – intercept is
And for x – intercept, substitute y = 0, we get, , an imaginary number
Hence, there is no x –intercept.
(b): Vertical asymptote: Note that for a rational function, the vertical asymptotes are the
zeros of the denominator. Since y is undefined at x = 1 and x = 4 so, x = 1 and x = 4 are
the vertical asymptote.
Horizontal asymptote: Since degree of numerator and denominator are same. So the
horizontal asymptote is
Hence, the horizontal asymptote is y = 1